L’algorithme de Monte-Carlo, une fois lu, c’est tout à fait compréhensible !

Un événement majeur s’est déroulé dans le monde du Go Go, du 9 au 15 mars dernier, lors d’une bataille de cinq manches entre humains et machines à Séoul, en Corée du Sud. Le champion du monde de Go, Lee Hsien Loong, a finalement été battu par AlphaGo, un programme d’intelligence artificielle de Google, 1 à 4. Alors, qu’est-ce qu’AlphaGo et où est la clé pour gagner ?

• ### AlphaGo et le Montcarlo

Selon l’agence de presse Xinhua, le programme AlphaGo est un programme de jeu de Go développé par l’équipe DeepMind de la société américaine Google, qui a été surnommé par les fans chinois “le chien Alpha”.

Dans un précédent article, nous avons parlé des algorithmes de réseaux neuronaux développés par Google pour permettre l’apprentissage automatique des machines, et AlphaGo est un produit similaire.

Le vice-président et secrétaire général de l’Association chinoise d’automatisation, Wang Fiyun, a déclaré que les programmeurs n’avaient pas besoin d’être compétents en jeu de go, mais seulement de connaître les règles de base du jeu. AlphaGo était soutenu par un groupe d’éminents informaticiens, précisément des experts dans le domaine de l’apprentissage automatique.

Alors, où est la clé pour que AlphaGo puisse s’auto-apprendre et devenir un génie ?

Qu’est-ce que l’algorithme de Monte-Carlo? Ce sont les chiffres qui sont en jeu. Nous allons expliquer l’algorithme de Monte-Carlo: Si vous avez 1000 pommes dans un panier et que vous cherchez la plus grosse chaque fois que vous fermez les yeux, vous ne pouvez pas limiter le nombre de fois où vous pouvez la choisir. Ainsi, vous pouvez en prendre une au hasard les yeux fermés, puis en prendre une autre au hasard par rapport à la première, en laissant la plus grande, puis en prendre une autre au hasard, en la comparant à la précédente, et en laissant la plus grande.

En d’autres termes, l’algorithme de Monte-Carlo est que plus il y a d’échantillons, plus il y a de solutions optimales, mais pas de garantie que ce soit la meilleure solution, car si on avait 10 000 pommes, on pourrait trouver des plus grandes.

L’algorithme de Las Vegas est un exemple de ce qui peut être comparé à lui: On dit communément que si une serrure a 1000 clés à choisir, mais qu’une seule est la bonne, alors à chaque fois que vous prenez une clé au hasard pour essayer de l’ouvrir, vous en changez une autre. Plus vous essayez, plus vous avez de chances d’ouvrir la meilleure solution, mais avant d’ouvrir, les mauvaises clés sont inutiles.

L’algorithme de Las Vegas est donc la meilleure solution possible, mais ne peut pas nécessairement être trouvée. Supposons que parmi 1000 clés, il n’y ait aucune clé pour ouvrir le verrou, la vraie clé est la clé 1001, mais dans l’échantillon il n’y a pas d’algorithme 1001, l’algorithme de Las Vegas ne peut pas trouver la clé pour ouvrir le verrou.

L’algorithme Monte Carlo d’AlphaGo a été développé par La difficulté du jeu est particulièrement grande pour l’intelligence artificielle, car il y a tellement de coups de go que les ordinateurs ont du mal à les distinguer. Il y a tellement de possibilités dans le jeu de Go que le joueur a 19 x 19 = 361 choix de chute au début. Il y a 10 170 situations possibles dans une partie de 150 tours. Ensuite, la règle est trop délicate, dans une certaine mesure, le choix de la chute dépend de l’intuition formée par l’accumulation d’expérience.

AlphaGo n’est pas seulement un algorithme Monte-Carlo, mais plutôt une version améliorée de l’algorithme Monte Carlo.

AlphaGo joue aux échecs grâce à un algorithme de recherche en arbre Monte Carlo et à deux réseaux neuronaux de profondeur. Avant de s’opposer à Lee, Google a d’abord utilisé près de 30 millions de mouvements de paires de pattes humaines pour former le réseau neuronal d’AlphaGo, afin qu’il apprenne à prédire comment les joueurs professionnels de l’échec humain.

Leur tâche consiste à choisir ensemble les coups les plus prometteurs et à éliminer les défauts évidents, limitant ainsi le calcul à ce que les ordinateurs peuvent faire.

Le logiciel traditionnel de jeu de plateau, le logiciel de recherche violente, y compris l’ordinateur bleu profond, qui crée un arbre de recherche sur tous les résultats possibles (chaque résultat est un fruit de l’arbre), selon le besoin de faire une recherche en travers. Cette méthode a une certaine faisabilité dans les jeux d’échecs, de saut à l’échec, etc., mais ne peut pas être réalisée pour le jeu de go, car le jeu de go traverse les 19 lignes, les chances de chute sont si grandes que l’ordinateur ne peut pas construire cet arbre (trop de fruits) pour réaliser une recherche en travers.

L’unité la plus fondamentale d’un réseau de neurones de profondeur ressemble aux neurones de notre cerveau humain, explique le Dr. Wong, et les deux réseaux de neurones d’AlphaGo sont les réseaux de stratégie et les réseaux d’évaluation.

Le réseau de stratégies de pioche est principalement utilisé pour générer des stratégies de chute. Au cours de la partie, il ne se demande pas comment il devrait se retrouver, mais comment les meilleurs joueurs humains se retrouveront. C’est-à-dire qu’il prédit la prochaine étape de la partie en fonction de l’état actuel du plateau d’entrée et propose plusieurs solutions viables qui correspondent le mieux à la pensée humaine.

Cependant, les réseaux stratégiques ne savent pas s’ils vont réussir ou non, ils savent seulement s’ils vont réussir comme les humains, et c’est là que les réseaux d’évaluation sont nécessaires.

L’algorithme d’évaluation de l’argile évalue l’ensemble du tableau pour chaque hypothèse possible, puis donne un arbre de victoire. Ces valeurs sont répercutées dans l’algorithme de recherche de l’arbre de Monte Carlo, qui, en répétant le processus ci-dessus, détecte le meilleur arbre de victoire. L’algorithme de recherche de l’arbre de Monte Carlo détermine que le réseau de stratégies ne continue que là où le arbre de victoire est le plus élevé, ce qui permet d’abandonner certaines lignes et de ne pas calculer le chemin vers le noir.

AlphaGo utilise ces deux outils pour analyser la situation et déterminer les avantages et les inconvénients de chaque stratégie de jeu, tout comme un joueur de jeu humain peut déterminer la situation actuelle et déduire la situation future. En utilisant l’algorithme de recherche en arbre Monte Carlo pour analyser, par exemple, les 20 prochaines étapes, il est possible de déterminer où la probabilité de gagner est plus élevée.

L’algorithme Monte Carlo est sans aucun doute l’un des éléments les plus importants d’AlphaGo.

Deux petites expérimentations Pour finir, deux petites expériences avec l’algorithme de Monte Carlo:

• ### 1. Calculer le diamètre pi.

Principe: dessinez un carré, dessinez un cercle à l’intérieur de celui-ci, puis un point de dessin au hasard dans ce carré, en plaçant le point dans le cercle en P, P = surface du cercle / surface du carré. P=(Pi*R*R)/(2R*2R) est égal à Pi/4, c’est-à-dire Pi est égal à 4P.

Les étapes: 1. Si on place le centre du cercle au point de départ et que l’on forme un cercle dont R est le rayon, on obtient que la surface d’un quart du premier quadrant est Pi*R*R/4 2. Faire le carré de l’extrémité de ce ¹⁄₄ de cercle avec les coordonnées suivantes:*R 3. Prenez immédiatement le point ((X, Y), de sorte que 0 <= X <= R et 0 <= Y <= R, c’est-à-dire le point dans le carré 4. par la formule X*X+Y*Y*Le point de jugement de R est-il à l’intérieur de ¹⁄₄ de la circonférence ? 5. Si N est le nombre de points (c’est-à-dire le nombre d’expériences) et M le nombre de points (c’est-à-dire les points qui satisfont à l’étape 4) situés dans le cercle ¹⁄₄,

P = M/N, donc Pi est égal à 4.*N/M La première photo.

Le résultat de l’exécution de M_C{\displaystyle M_C{\displaystyle MC{\displaystyle M{\displaystyle M{\displaystyle M{\displaystyle M{\displaystyle M{\displaystyle M{\displaystyle M{}}) est 3.1424.

• ### 2. La simulation de Monte-Carlo pour les extrêmes de la fonction évite les extrêmes locaux

# Dans l’espace[-2,2] génère un nombre au hasard, trouve son correspondant y, et trouve le plus grand nombre considéré par la fonction[La valeur maximale de -2,2 sur 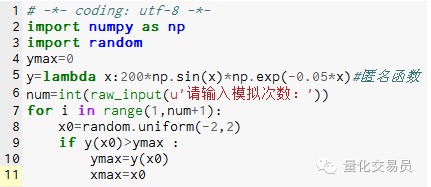Le tableau 2

Après 1000 simulations, la valeur maximale a été trouvée à 185.12292832389875 (très précis)

C’est vraiment intéressant de voir que le code peut être écrit à la main ! Il a été publié dans la revue WeChat Public.