Réflexions sur les stratégies de trading haute fréquence (2)
 1
1
 3416
3416
L’article traite principalement des stratégies de trading à haute fréquence, en se concentrant sur la modélisation du volume cumulatif et des chocs de prix. Cet article propose un modèle préliminaire de placement optimal des ordres en analysant l’impact des transactions uniques, des chocs de prix à intervalle fixe et du volume des transactions sur les prix. Ce modèle tente de trouver la position de trading optimale en fonction de la compréhension des chocs de volume et de prix. Les hypothèses du modèle sont discutées en profondeur et une évaluation préliminaire du placement optimal des commandes est effectuée en comparant les rendements attendus réels et prévus par le modèle.
Modélisation des volumes cumulés
L’article précédent a dérivé l’expression de probabilité pour qu’un volume de transaction unique soit supérieur à une certaine valeur :
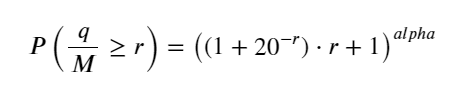
Nous nous inquiétons également de la répartition du volume des transactions sur une période donnée, qui devrait intuitivement être liée au volume de chaque transaction et à la fréquence des ordres. Ensuite, les données sont traitées à intervalles fixes. Tracez sa distribution comme ci-dessus.
from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
trades = pd.read_csv('HOOKUSDT-aggTrades-2023-01-27.csv')
trades['date'] = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index = trades['date']
buy_trades = trades[trades['is_buyer_maker']==False].copy()
buy_trades = buy_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
buy_trades['interval']=buy_trades['transact_time'] - buy_trades['transact_time'].shift()
buy_trades.index = buy_trades['date']
Fusionnez le volume de transactions toutes les 1 secondes, supprimez la partie où aucune transaction n’a eu lieu et utilisez la distribution de transaction unique ci-dessus pour l’ajuster. On peut voir que le résultat est meilleur. Si toutes les transactions en 1 secondes sont considérées comme des transactions uniques, ce problème devient C’est devenu un problème résolu. Cependant, lorsque le cycle est allongé (par rapport à la fréquence des transactions), l’erreur augmente et les recherches ont montré que cette erreur est causée par le terme de correction de la distribution de Pareto précédente. Cela signifie que lorsque le cycle s’allonge et inclut davantage de transactions individuelles, la combinaison de plusieurs transactions se rapproche de la distribution de Pareto. Dans ce cas, le terme de correction doit être supprimé.
df_resampled = buy_trades['quantity'].resample('1S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
buy_trades
| agg_trade_id | price | quantity | first_trade_id | last_trade_id | is_buyer_maker | date | transact_time | interval | diff | |
|---|---|---|---|---|---|---|---|---|---|---|
| 2023-01-27 00:00:00.161 | 1138369 | 2.901 | 54.3 | 3806199 | 3806201 | False | 2023-01-27 00:00:00.161 | 1674777600161 | NaN | 0.001 |
| 2023-01-27 00:00:04.140 | 1138370 | 2.901 | 291.3 | 3806202 | 3806203 | False | 2023-01-27 00:00:04.140 | 1674777604140 | 3979.0 | 0.000 |
| 2023-01-27 00:00:04.339 | 1138373 | 2.902 | 55.1 | 3806205 | 3806207 | False | 2023-01-27 00:00:04.339 | 1674777604339 | 199.0 | 0.001 |
| 2023-01-27 00:00:04.772 | 1138374 | 2.902 | 1032.7 | 3806208 | 3806223 | False | 2023-01-27 00:00:04.772 | 1674777604772 | 433.0 | 0.000 |
| 2023-01-27 00:00:05.562 | 1138375 | 2.901 | 3.5 | 3806224 | 3806224 | False | 2023-01-27 00:00:05.562 | 1674777605562 | 790.0 | 0.000 |
| … | … | … | … | … | … | … | … | … | … | … |
| 2023-01-27 23:59:57.739 | 1544370 | 3.572 | 394.8 | 5074645 | 5074651 | False | 2023-01-27 23:59:57.739 | 1674863997739 | 1224.0 | 0.002 |
| 2023-01-27 23:59:57.902 | 1544372 | 3.573 | 177.6 | 5074652 | 5074655 | False | 2023-01-27 23:59:57.902 | 1674863997902 | 163.0 | 0.001 |
| 2023-01-27 23:59:58.107 | 1544373 | 3.573 | 139.8 | 5074656 | 5074656 | False | 2023-01-27 23:59:58.107 | 1674863998107 | 205.0 | 0.000 |
| 2023-01-27 23:59:58.302 | 1544374 | 3.573 | 60.5 | 5074657 | 5074657 | False | 2023-01-27 23:59:58.302 | 1674863998302 | 195.0 | 0.000 |
| 2023-01-27 23:59:59.894 | 1544376 | 3.571 | 12.1 | 5074662 | 5074664 | False | 2023-01-27 23:59:59.894 | 1674863999894 | 1592.0 | 0.000 |
#1s内的累计分布
depths = np.array(range(0, 3000, 5))
probabilities = np.array([np.mean(df_resampled['quantity'] > depth) for depth in depths])
mean = df_resampled['quantity'].mean()
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([((1+20**(-depth/mean))*depth/mean+1)**(alpha) for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)
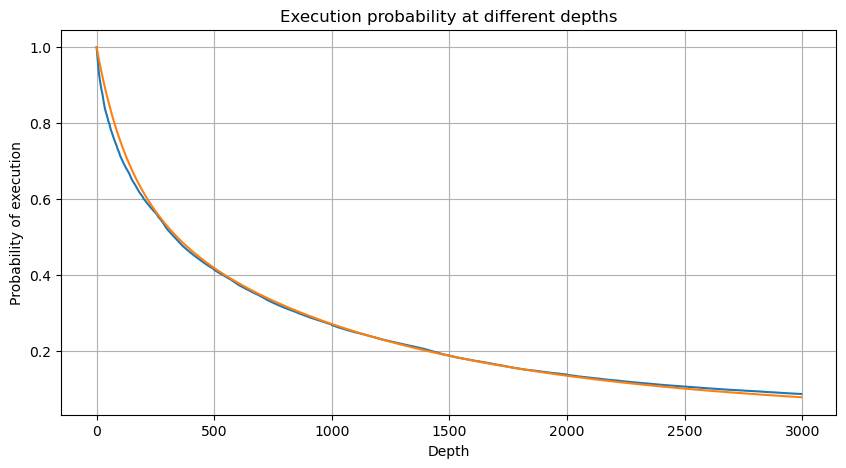
df_resampled = buy_trades['quantity'].resample('30S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
depths = np.array(range(0, 12000, 20))
probabilities = np.array([np.mean(df_resampled['quantity'] > depth) for depth in depths])
mean = df_resampled['quantity'].mean()
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([((1+20**(-depth/mean))*depth/mean+1)**(alpha) for depth in depths])
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2)
probabilities_s_2 = np.array([(depth/mean+1)**alpha for depth in depths]) # 无修正
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities,label='Probabilities (True)')
plt.plot(depths, probabilities_s, label='Probabilities (Simulation 1)')
plt.plot(depths, probabilities_s_2, label='Probabilities (Simulation 2)')
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.legend()
plt.grid(True)
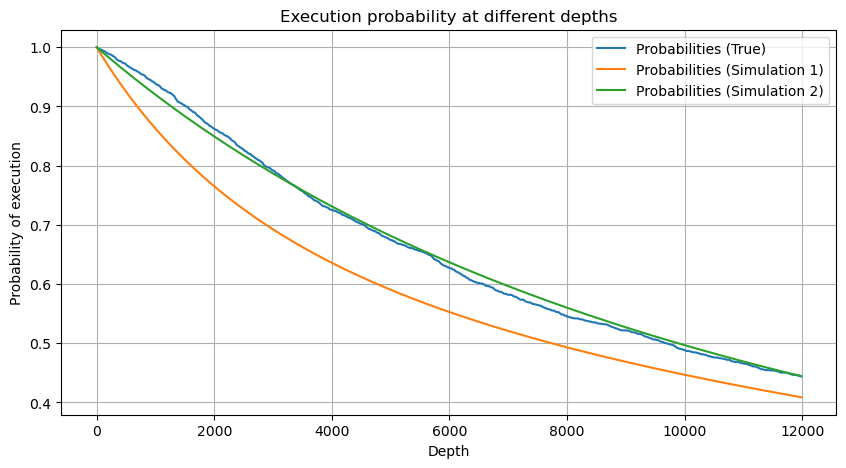
Nous avons maintenant résumé une formule générale pour la distribution du volume de transactions accumulé à différents moments, et utilisé la distribution des transactions individuelles pour l’ajuster, sans avoir à les compter séparément à chaque fois. Ici, nous omettons le processus et donnons directement la formule :
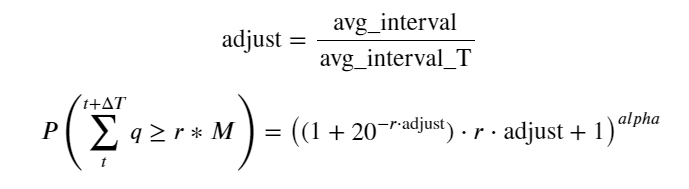
Parmi eux, avg_interval représente l’intervalle moyen entre les transactions individuelles et avg_interval_T représente l’intervalle moyen des intervalles qui doivent être estimés. C’est un peu déroutant. Si nous voulons estimer le temps de transaction d’une seconde, nous devons calculer l’intervalle moyen entre les événements contenant des transactions dans un délai d’une seconde. Si la probabilité d’arrivée d’une commande est conforme à la distribution de Poisson, il devrait être possible de l’estimer directement ici, mais l’écart réel est grand, je ne l’expliquerai donc pas ici.
Notez que la probabilité que le volume soit supérieur à une certaine valeur dans un certain intervalle doit être assez différente de la probabilité réelle de la transaction à cette position dans la profondeur, car plus le temps d’attente est long, plus la possibilité que le carnet d’ordres soit La profondeur change, de sorte que la probabilité de transaction à la même position de profondeur change en temps réel à mesure que les données sont mises à jour.
df_resampled = buy_trades['quantity'].resample('2S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
depths = np.array(range(0, 6500, 10))
probabilities = np.array([np.mean(df_resampled['quantity'] > depth) for depth in depths])
mean = buy_trades['quantity'].mean()
adjust = buy_trades['interval'].mean() / 2620
alpha = np.log(np.mean(buy_trades['quantity'] > mean))/0.7178397931503168
probabilities_s = np.array([((1+20**(-depth*adjust/mean))*depth*adjust/mean+1)**(alpha) for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)
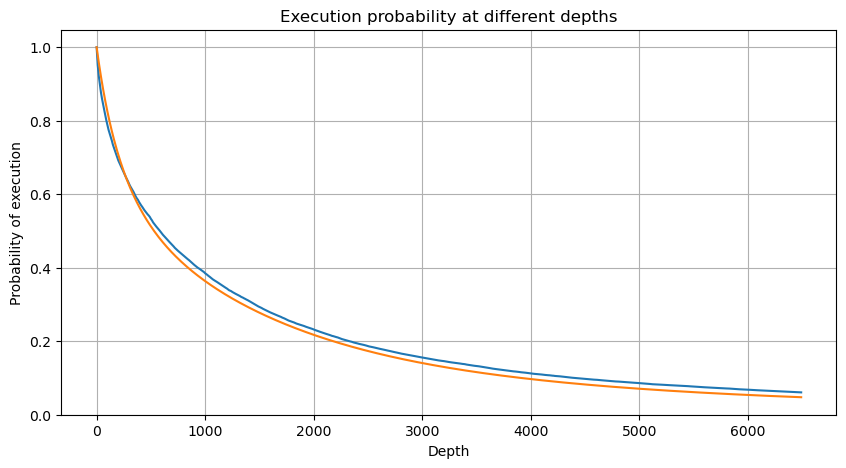
Impact sur le prix d’une transaction unique
Les données de transaction sont un trésor, et il reste encore beaucoup de données à exploiter. Nous devons prêter une attention particulière à l’impact des commandes sur les prix, ce qui affecte le placement des commandes en attente dans la stratégie. De même, en fonction des données agrégées transact_time, calculez la différence entre le dernier prix et le premier prix. S’il n’y a qu’une seule commande, la différence est de 0. Ce qui est étrange, c’est qu’il existe encore un petit nombre de résultats de données avec des résultats négatifs. Il s’agit probablement d’un problème lié à l’ordre de disposition des données, je n’entrerai donc pas dans les détails ici.
Les résultats montrent que la proportion d’aucun impact est aussi élevée que 77 %, la proportion de 1 tick est de 16,5 %, 2 ticks est de 3,7 %, 3 ticks est de 1,2 % et la proportion de plus de 4 ticks est inférieure à 1 % . Cela correspond fondamentalement aux caractéristiques de la fonction exponentielle, mais l’ajustement n’est pas précis.
Le volume de transaction qui a provoqué la différence de prix correspondante a été compté et la distorsion causée par un impact trop important a été supprimée. Cela correspond fondamentalement à la relation linéaire et environ tous les 1 000 volumes provoquent une fluctuation de prix d’un tick. On peut également comprendre que le nombre moyen d’ordres en attente à proximité de chaque prix est d’environ 1 000.
diff_df = trades[trades['is_buyer_maker']==False].groupby('transact_time')['price'].agg(lambda x: abs(round(x.iloc[-1] - x.iloc[0],3)) if len(x) > 1 else 0)
buy_trades['diff'] = buy_trades['transact_time'].map(diff_df)
diff_counts = buy_trades['diff'].value_counts()
diff_counts[diff_counts>10]/diff_counts.sum()
0.000 0.769965
0.001 0.165527
0.002 0.037826
0.003 0.012546
0.004 0.005986
0.005 0.003173
0.006 0.001964
0.007 0.001036
0.008 0.000795
0.009 0.000474
0.010 0.000227
0.011 0.000187
0.012 0.000087
0.013 0.000080
Name: diff, dtype: float64
diff_group = buy_trades.groupby('diff').agg({
'quantity': 'mean',
'diff': 'last',
})
diff_group['quantity'][diff_group['diff']>0][diff_group['diff']<0.01].plot(figsize=(10,5),grid=True);
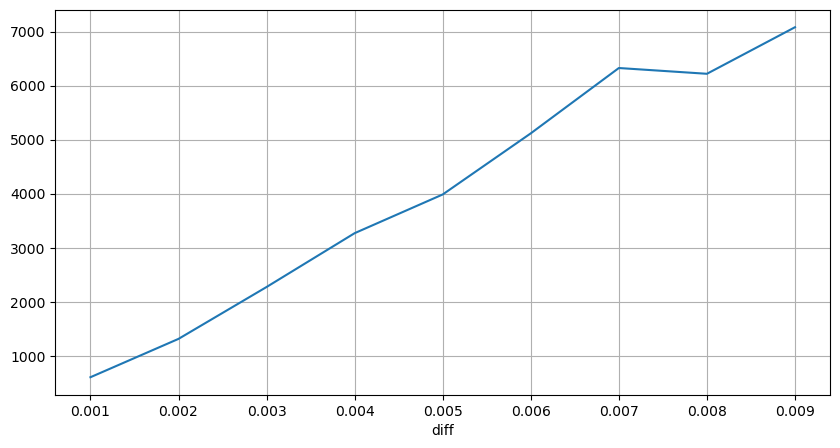
Chocs de prix à intervalles réguliers
Comptez l’impact du prix dans les 2 secondes. La différence ici est qu’il y aura des valeurs négatives. Bien sûr, comme seuls les ordres d’achat sont comptabilisés ici, la position symétrique sera plus grande d’un tick. Continuez à observer la relation entre le volume de transactions et l’impact, et ne comptez que les résultats supérieurs à 0. La conclusion est similaire à celle d’un ordre unique, qui est également une relation linéaire approximative. Chaque tick nécessite environ 2000 volumes.
df_resampled = buy_trades.resample('2S').agg({
'price': ['first', 'last', 'count'],
'quantity': 'sum'
})
df_resampled['price_diff'] = round(df_resampled[('price', 'last')] - df_resampled[('price', 'first')],3)
df_resampled['price_diff'] = df_resampled['price_diff'].fillna(0)
result_df_raw = pd.DataFrame({
'price_diff': df_resampled['price_diff'],
'quantity_sum': df_resampled[('quantity', 'sum')],
'data_count': df_resampled[('price', 'count')]
})
result_df = result_df_raw[result_df_raw['price_diff'] != 0]
result_df['price_diff'][abs(result_df['price_diff'])<0.016].value_counts().sort_index().plot.bar(figsize=(10,5));
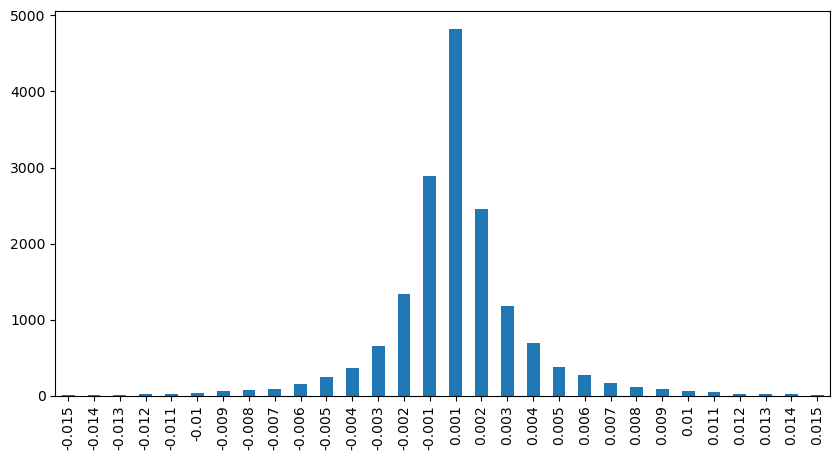
result_df['price_diff'].value_counts()[result_df['price_diff'].value_counts()>30]
0.001 7176
-0.001 3665
0.002 3069
-0.002 1536
0.003 1260
0.004 692
-0.003 608
0.005 391
-0.004 322
0.006 259
-0.005 192
0.007 146
-0.006 112
0.008 82
0.009 75
-0.007 75
-0.008 65
0.010 51
0.011 41
-0.010 31
Name: price_diff, dtype: int64
diff_group = result_df.groupby('price_diff').agg({ 'quantity_sum': 'mean'})
diff_group[(diff_group.index>0) & (diff_group.index<0.015)].plot(figsize=(10,5),grid=True);
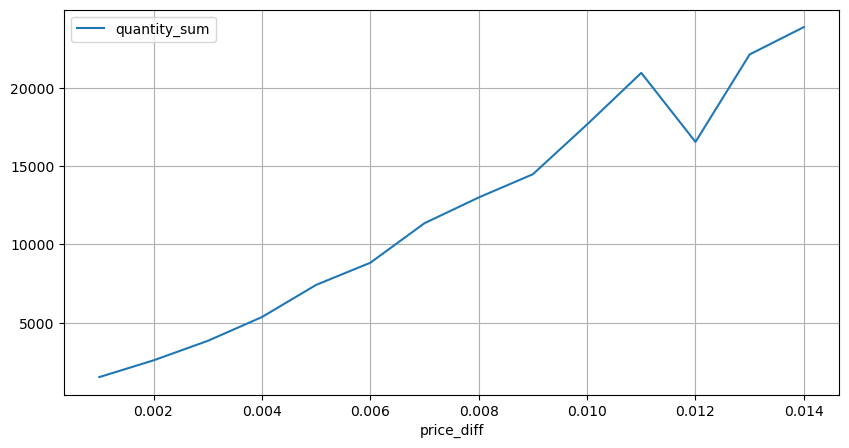
Impact du volume sur les prix
Le volume requis pour un changement de tick a été calculé précédemment, mais il n’est pas précis car il est basé sur l’hypothèse que l’impact s’est déjà produit. Voyons maintenant l’impact sur les prix causé par le volume des transactions.
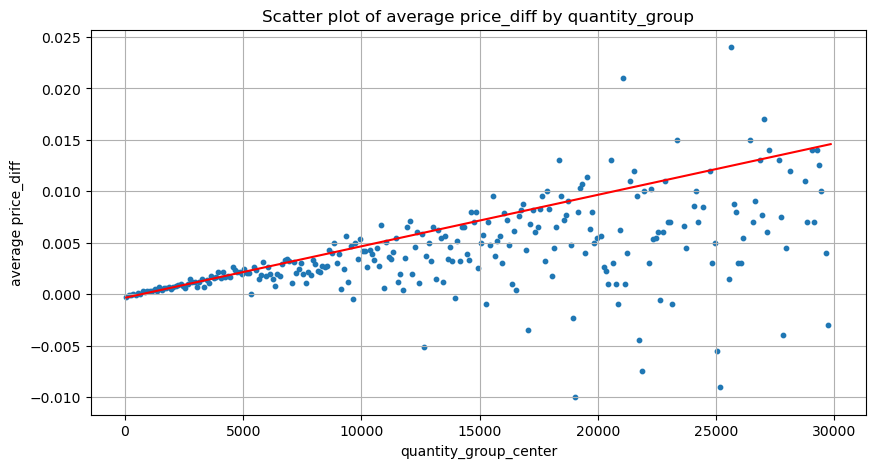
Les données ici sont échantillonnées à 1 seconde, avec 100 quantités par étape, et les variations de prix dans cette plage de quantités sont comptées. Quelques conclusions précieuses ont été tirées :
- Lorsque le volume d’achat est inférieur à 500, la variation de prix attendue est à la baisse, ce qui est attendu car il existe également des ordres de vente affectant le prix.
- Lorsque le volume des transactions est faible, il suit une relation linéaire, c’est-à-dire que plus le volume des transactions est important, plus l’augmentation des prix est importante.
- Plus le volume de l’ordre d’achat est important, plus le changement de prix est important, ce qui représente souvent une percée de prix. Après la percée, le prix peut revenir. Associées à l’échantillonnage à intervalles fixes, les données sont instables.
- Il convient de prêter attention à la partie supérieure du nuage de points, c’est-à-dire à la partie où le volume correspond à l’augmentation des prix.
- Pour cette paire de trading uniquement, une version approximative de la relation entre le volume et la variation de prix est donnée :
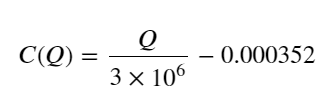
Parmi eux, « C » représente la variation de prix et « Q » représente le volume de l’ordre d’achat.
df_resampled = buy_trades.resample('1S').agg({
'price': ['first', 'last', 'count'],
'quantity': 'sum'
})
df_resampled['price_diff'] = round(df_resampled[('price', 'last')] - df_resampled[('price', 'first')],3)
df_resampled['price_diff'] = df_resampled['price_diff'].fillna(0)
result_df_raw = pd.DataFrame({
'price_diff': df_resampled['price_diff'],
'quantity_sum': df_resampled[('quantity', 'sum')],
'data_count': df_resampled[('price', 'count')]
})
result_df = result_df_raw[result_df_raw['price_diff'] != 0]
df = result_df.copy()
bins = np.arange(0, 30000, 100) #
labels = [f'{i}-{i+100-1}' for i in bins[:-1]]
df.loc[:, 'quantity_group'] = pd.cut(df['quantity_sum'], bins=bins, labels=labels)
grouped = df.groupby('quantity_group')['price_diff'].mean()
grouped_df = pd.DataFrame(grouped).reset_index()
grouped_df['quantity_group_center'] = grouped_df['quantity_group'].apply(lambda x: (float(x.split('-')[0]) + float(x.split('-')[1])) / 2)
plt.figure(figsize=(10,5))
plt.scatter(grouped_df['quantity_group_center'], grouped_df['price_diff'],s=10)
plt.plot(grouped_df['quantity_group_center'], np.array(grouped_df['quantity_group_center'].values)/2e6-0.000352,color='red')
plt.xlabel('quantity_group_center')
plt.ylabel('average price_diff')
plt.title('Scatter plot of average price_diff by quantity_group')
plt.grid(True)
grouped_df.head(10)
| quantity_group | price_diff | quantity_group_center | |
|---|---|---|---|
| 0 | 0-199 | -0.000302 | 99.5 |
| 1 | 100-299 | -0.000124 | 199.5 |
| 2 | 200-399 | -0.000068 | 299.5 |
| 3 | 300-499 | -0.000017 | 399.5 |
| 4 | 400-599 | -0.000048 | 499.5 |
| 5 | 500-699 | 0.000098 | 599.5 |
| 6 | 600-799 | 0.000006 | 699.5 |
| 7 | 700-899 | 0.000261 | 799.5 |
| 8 | 800-999 | 0.000186 | 899.5 |
| 9 | 900-1099 | 0.000299 | 999.5 |
Position de commande optimale initiale
Avec la modélisation du volume des transactions et un modèle approximatif du volume des transactions correspondant à l’impact sur les prix, il semble que la position d’ordre optimale puisse être calculée. Faisons quelques hypothèses et donnons une position de prix optimale irresponsable.
- Supposons que le prix revienne à sa valeur initiale après le choc (ce qui est bien sûr peu probable et nécessite une réanalyse des variations de prix après le choc)
- Supposons que la distribution du volume des transactions et de la fréquence des ordres au cours de cette période réponde aux exigences prédéfinies (ce qui est également inexact, car la valeur d’un jour est utilisée pour l’estimation et les transactions présentent un regroupement évident).
- Supposons qu’un seul ordre de vente se produise pendant la période de simulation, puis que la position soit fermée.
- En supposant qu’après l’exécution de l’ordre, d’autres ordres d’achat continuent de faire monter le prix, surtout lorsque le volume est très faible. Cet effet est ici ignoré et on suppose simplement qu’il reviendra.
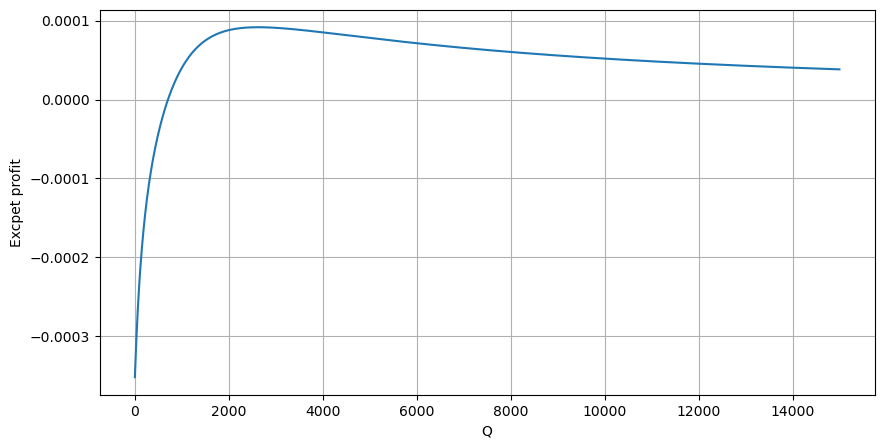
Tout d’abord, écrivez un rendement attendu simple, c’est-à-dire la probabilité que l’ordre d’achat cumulé soit supérieur à Q dans un délai d’une seconde, multipliée par le taux de rendement attendu (c’est-à-dire le prix d’impact) :
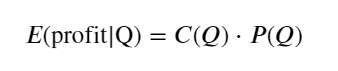
Selon le graphique, le rendement attendu est maximal autour de 2 500, ce qui représente environ 2,5 fois le volume moyen des transactions. C’est-à-dire que l’ordre de vente doit être placé à 2500. Il convient de souligner à nouveau que l’axe horizontal représente le volume des transactions sur une seconde et ne peut pas être simplement assimilé à la position de profondeur. Et cela à un moment où il y a encore un manque de données approfondies très importantes, et cela ne repose que sur des spéculations basées sur des transactions.
Résumer
On constate que la distribution du volume à différents intervalles de temps est une simple mise à l’échelle de la distribution du volume d’une transaction unique. Nous avons également réalisé un modèle simple de rendement attendu basé sur les chocs de prix et la probabilité de transaction. Les résultats de ce modèle sont conformes à nos attentes. Si le volume de l’ordre de vente est faible, cela indique une baisse de prix. Un certain volume est nécessaire pour Les marges bénéficiaires sont d’autant plus élevées que le volume de transactions est important. Plus la probabilité est élevée, plus elle est faible. Il existe une taille optimale au milieu, qui correspond également à la position de placement de l’ordre recherchée par la stratégie. Bien sûr, ce modèle est encore trop simple. Dans le prochain article, je continuerai à en discuter en profondeur.
#1s内的累计分布
df_resampled = buy_trades['quantity'].resample('1S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
depths = np.array(range(0, 15000, 10))
mean = df_resampled['quantity'].mean()
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([((1+20**(-depth/mean))*depth/mean+1)**(alpha) for depth in depths])
profit_s = np.array([depth/2e6-0.000352 for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities_s*profit_s)
plt.xlabel('Q')
plt.ylabel('Excpet profit')
plt.grid(True)