L’article précédent a donné une introduction préliminaire aux méthodes de calcul des différents prix moyens et a donné une révision du prix moyen. Cet article continue d’approfondir ce sujet.

Données requises

Les données de flux d’ordres et les dix niveaux de données de profondeur sont collectés à partir de transactions réelles et la fréquence de mise à jour est de 100 ms. Le marché réel ne contient que les données d’achat et de vente, qui sont mises à jour en temps réel. Pour des raisons de simplicité, il n’est pas utilisé pour le moment. Étant donné que les données sont trop volumineuses, seules 100 000 lignes de données approfondies sont conservées et les conditions du marché pour chaque niveau sont également séparées en colonnes distinctes.

from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import ast
%matplotlib inline

tick_size = 0.0001

trades = pd.read_csv('YGGUSDT_aggTrade.csv',names=['type','event_time', 'agg_trade_id','symbol', 'price', 'quantity', 'first_trade_id', 'last_trade_id',
       'transact_time', 'is_buyer_maker'])

trades = trades.groupby(['transact_time','is_buyer_maker']).agg({
    'transact_time':'last',
    'agg_trade_id': 'last',
    'price': 'first',
    'quantity': 'sum',
    'first_trade_id': 'first',
    'last_trade_id': 'last',
    'is_buyer_maker': 'last',
})

trades.index = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index.rename('time', inplace=True)
trades['interval'] = trades['transact_time'] - trades['transact_time'].shift()

depths = pd.read_csv('YGGUSDT_depth.csv',names=['type','event_time', 'transact_time','symbol', 'u1', 'u2', 'u3', 'bids','asks'])

depths = depths.iloc[:100000]

depths['bids'] = depths['bids'].apply(ast.literal_eval).copy()
depths['asks'] = depths['asks'].apply(ast.literal_eval).copy()

def expand_bid(bid_data):
    expanded = {}
    for j, (price, quantity) in enumerate(bid_data):
        expanded[f'bid_{j}_price'] = float(price)
        expanded[f'bid_{j}_quantity'] = float(quantity)
    return pd.Series(expanded)
def expand_ask(ask_data):
    expanded = {}
    for j, (price, quantity) in enumerate(ask_data):
        expanded[f'ask_{j}_price'] = float(price)
        expanded[f'ask_{j}_quantity'] = float(quantity)
    return pd.Series(expanded)
# 应用到每一行，得到新的df
expanded_df_bid = depths['bids'].apply(expand_bid)
expanded_df_ask = depths['asks'].apply(expand_ask)
# 在原有df上进行扩展
depths = pd.concat([depths, expanded_df_bid, expanded_df_ask], axis=1)

depths.index = pd.to_datetime(depths['transact_time'], unit='ms')
depths.index.rename('time', inplace=True);

trades = trades[trades['transact_time'] < depths['transact_time'].iloc[-1]]

Regardons d’abord la distribution de ces 20 conditions de marché. Elle est conforme aux attentes. Plus on s’éloigne de l’ouverture du marché, plus il y a d’ordres en attente, et les ordres d’achat et de vente sont à peu près symétriques.

bid_mean_list = []
ask_mean_list = []
for i in range(20):
    bid_mean_list.append(round(depths[f'bid_{i}_quantity'].mean(),0))
    ask_mean_list.append(round(depths[f'ask_{i}_quantity'].mean(),0))
plt.figure(figsize=(10, 5))
plt.plot(bid_mean_list);
plt.plot(ask_mean_list);
plt.grid(True)

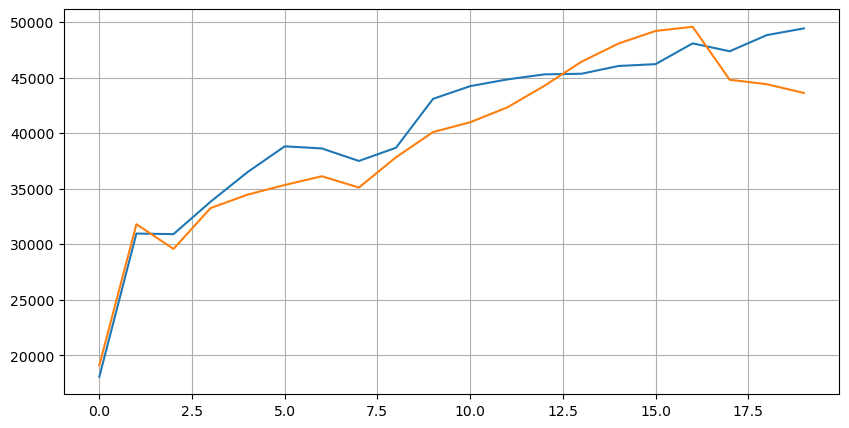
Combinez les données de profondeur et les données de transaction pour faciliter l’évaluation de la précision des prévisions. Ici, nous nous assurons que les données de transaction sont toutes postérieures aux données de profondeur. Sans tenir compte du retard, nous calculons directement l’erreur quadratique moyenne entre la valeur prédite et le prix réel de la transaction. Utilisé pour mesurer la précision des prédictions.

À en juger par les résultats, l’erreur de mid_price, la moyenne de la paire achat-vente, est la plus importante. Après avoir changé pour weight_mid_price, l’erreur devient immédiatement beaucoup plus petite, et elle est encore améliorée en ajustant le prix moyen pondéré. Après la publication de l’article d’hier, certaines personnes ont signalé qu’elles n’avaient utilisé que 1^³⁄₂. J’ai vérifié ici et j’ai constaté que le résultat était meilleur. Après avoir réfléchi à la raison, il s’agit probablement de la différence de fréquence des événements. Lorsque I est proche de -1 et 1, il s’agit d’un événement à faible probabilité. Afin de corriger ces faibles probabilités, la prédiction d’événements à haute fréquence n’est pas si précis. Par conséquent, afin de mieux prendre en compte les événements à haute fréquence, j’ai effectué quelques ajustements (ce sont des paramètres purement expérimentaux et ne sont pas très utiles pour le trading réel) :

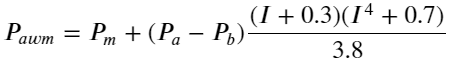
Le résultat était légèrement meilleur. Comme mentionné dans l’article précédent, les stratégies doivent être prédites avec plus de données. Avec plus de profondeur et de données sur l’exécution des commandes, l’amélioration qui peut être obtenue par intrication avec le prix du marché est déjà très faible.

df = pd.merge_asof(trades, depths, on='transact_time', direction='backward')

df['spread'] = round(df['ask_0_price'] - df['bid_0_price'],4)
df['mid_price'] = (df['bid_0_price']+ df['ask_0_price']) / 2
df['I'] = (df['bid_0_quantity'] - df['ask_0_quantity']) / (df['bid_0_quantity'] + df['ask_0_quantity'])
df['weight_mid_price'] = df['mid_price'] + df['spread']*df['I']/2
df['adjust_mid_price'] = df['mid_price'] + df['spread']*(df['I'])*(df['I']**8+1)/4
df['adjust_mid_price_2'] = df['mid_price'] + df['spread']*df['I']*(df['I']**2+1)/4
df['adjust_mid_price_3'] = df['mid_price'] + df['spread']*df['I']**3/2
df['adjust_mid_price_4'] = df['mid_price'] + df['spread']*(df['I']+0.3)*(df['I']**4+0.7)/3.8

print('平均值     mid_price的误差：', ((df['price']-df['mid_price'])**2).sum())
print('挂单量加权 mid_price的误差：', ((df['price']-df['weight_mid_price'])**2).sum())
print('调整后的   mid_price的误差：', ((df['price']-df['adjust_mid_price'])**2).sum())
print('调整后的 mid_price_2的误差：', ((df['price']-df['adjust_mid_price_2'])**2).sum())
print('调整后的 mid_price_3的误差：', ((df['price']-df['adjust_mid_price_3'])**2).sum())
print('调整后的 mid_price_4的误差：', ((df['price']-df['adjust_mid_price_4'])**2).sum())

平均值     mid_price的误差： 0.0048751924999999845
挂单量加权 mid_price的误差： 0.0048373440193987035
调整后的   mid_price的误差： 0.004803654771638586
调整后的 mid_price_2的误差： 0.004808216498329721
调整后的 mid_price_3的误差： 0.004794984755260528
调整后的 mid_price_4的误差： 0.0047909595497071375

Tenez compte de la profondeur du deuxième engrenage

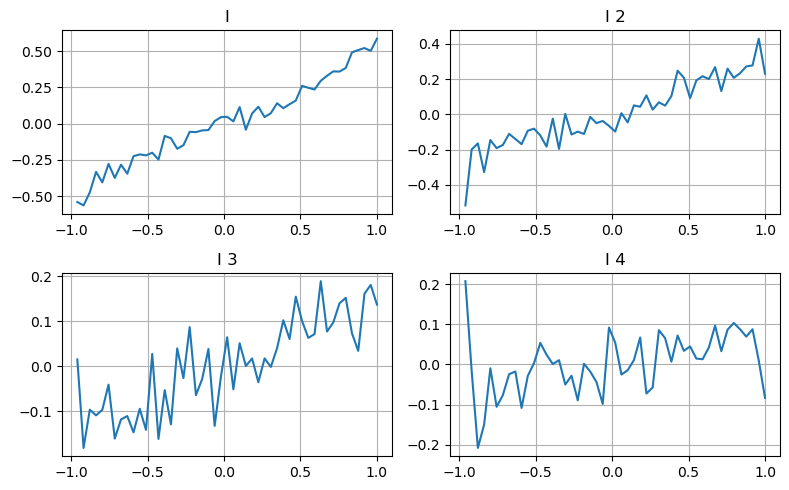
Nous utilisons ici l’idée de l’article précédent pour examiner les différentes plages de valeurs d’un certain paramètre d’influence et les variations du prix de transaction pour mesurer la contribution de ce paramètre au prix moyen. Comme le montre le graphique de profondeur de premier niveau, à mesure que I augmente, le prix de la prochaine transaction est plus susceptible de changer positivement, ce qui signifie que I apporte une contribution positive.

Le deuxième lot a été traité de la même manière et il a été constaté que même si l’effet était légèrement inférieur à celui du premier lot, il n’était toujours pas négligeable. Le troisième niveau de profondeur apporte également une légère contribution, mais la monotonie est bien pire et les profondeurs plus importantes n’ont fondamentalement aucune valeur de référence.

Selon les différents niveaux de contribution, des pondérations différentes sont attribuées aux paramètres de déséquilibre des trois niveaux. L’inspection réelle montre que les erreurs de prédiction sont encore réduites pour différentes méthodes de calcul.

bins = np.linspace(-1, 1, 50)
df['change'] = (df['price'].pct_change().shift(-1))/tick_size
df['I_bins'] = pd.cut(df['I'], bins, labels=bins[1:])
df['I_2'] = (df['bid_1_quantity'] - df['ask_1_quantity']) / (df['bid_1_quantity'] + df['ask_1_quantity'])
df['I_2_bins'] = pd.cut(df['I_2'], bins, labels=bins[1:])
df['I_3'] = (df['bid_2_quantity'] - df['ask_2_quantity']) / (df['bid_2_quantity'] + df['ask_2_quantity'])
df['I_3_bins'] = pd.cut(df['I_3'], bins, labels=bins[1:])
df['I_4'] = (df['bid_3_quantity'] - df['ask_3_quantity']) / (df['bid_3_quantity'] + df['ask_3_quantity'])
df['I_4_bins'] = pd.cut(df['I_4'], bins, labels=bins[1:])
fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(8, 5))


axes[0][0].plot(df.groupby('I_bins')['change'].mean())
axes[0][0].set_title('I')
axes[0][0].grid(True)

axes[0][1].plot(df.groupby('I_2_bins')['change'].mean())
axes[0][1].set_title('I 2')
axes[0][1].grid(True)

axes[1][0].plot(df.groupby('I_3_bins')['change'].mean())
axes[1][0].set_title('I 3')
axes[1][0].grid(True)

axes[1][1].plot(df.groupby('I_4_bins')['change'].mean())
axes[1][1].set_title('I 4')
axes[1][1].grid(True)
plt.tight_layout();

df['adjust_mid_price_4'] = df['mid_price'] + df['spread']*(df['I']+0.3)*(df['I']**4+0.7)/3.8
df['adjust_mid_price_5'] = df['mid_price'] + df['spread']*(0.7*df['I']+0.3*df['I_2'])/2
df['adjust_mid_price_6'] = df['mid_price'] + df['spread']*(0.7*df['I']+0.3*df['I_2'])**3/2
df['adjust_mid_price_7'] = df['mid_price'] + df['spread']*(0.7*df['I']+0.3*df['I_2']+0.3)*((0.7*df['I']+0.3*df['I_2'])**4+0.7)/3.8
df['adjust_mid_price_8'] = df['mid_price'] + df['spread']*(0.7*df['I']+0.2*df['I_2']+0.1*df['I_3']+0.3)*((0.7*df['I']+0.3*df['I_2']+0.1*df['I_3'])**4+0.7)/3.8

print('调整后的 mid_price_4的误差：', ((df['price']-df['adjust_mid_price_4'])**2).sum())
print('调整后的 mid_price_5的误差：', ((df['price']-df['adjust_mid_price_5'])**2).sum())
print('调整后的 mid_price_6的误差：', ((df['price']-df['adjust_mid_price_6'])**2).sum())
print('调整后的 mid_price_7的误差：', ((df['price']-df['adjust_mid_price_7'])**2).sum())
print('调整后的 mid_price_8的误差：', ((df['price']-df['adjust_mid_price_8'])**2).sum())

调整后的 mid_price_4的误差： 0.0047909595497071375
调整后的 mid_price_5的误差： 0.0047884350488318714
调整后的 mid_price_6的误差： 0.0047778319053133735
调整后的 mid_price_7的误差： 0.004773578540592192
调整后的 mid_price_8的误差： 0.004771415189297518

Tenir compte des données de transaction

Les données de transaction reflètent directement le degré de positions longues et courtes. Après tout, il s’agit d’une option qui implique de l’argent réel, et le coût de passation d’une commande est bien inférieur, et il existe même des cas de fraude délibérée au placement d’une commande. Par conséquent, lors de la prévision du prix moyen, la stratégie doit se concentrer sur les données de transaction.

Considérant la forme, définissez le déséquilibre de la quantité moyenne d’arrivée des commandes VI, Vb, Vs représentant respectivement la quantité moyenne d’ordres d’achat et d’ordres de vente au sein d’un événement unitaire.

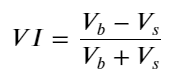
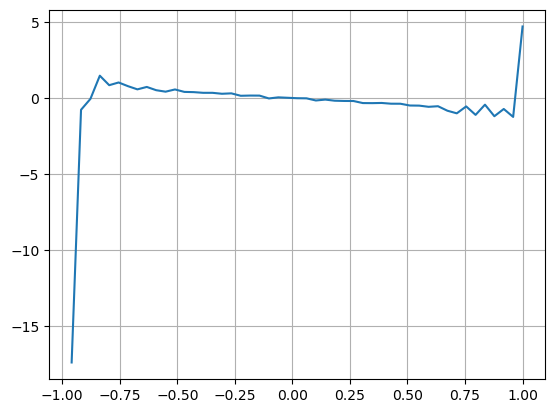
Les résultats montrent que la quantité d’arrivée dans un court laps de temps est la plus significative pour prédire les changements de prix. Lorsque l’IV est compris entre (0,1-0,9), il est négativement corrélé au prix, mais en dehors de cette plage, il est positivement corrélé au prix. prix. Cela suggère que lorsque le marché n’est pas extrême, il est principalement caractérisé par des fluctuations et les prix reviennent à la moyenne. Lorsque des conditions de marché extrêmes se produisent, comme un grand nombre d’ordres d’achat dépassant les ordres de vente, la tendance s’écarte de la tendance. . Même si nous ignorons ces situations de faible probabilité et supposons simplement que la tendance et l’IV satisfont une relation linéaire négative, l’erreur de prédiction du prix moyen est considérablement réduite. Le a dans la formule représente le coefficient.

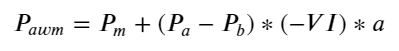
alpha=0.1

df['avg_buy_interval'] = None
df['avg_sell_interval'] = None
df.loc[df['is_buyer_maker'] == True, 'avg_buy_interval'] = df[df['is_buyer_maker'] == True]['transact_time'].diff().ewm(alpha=alpha).mean()
df.loc[df['is_buyer_maker'] == False, 'avg_sell_interval'] = df[df['is_buyer_maker'] == False]['transact_time'].diff().ewm(alpha=alpha).mean()

df['avg_buy_quantity'] = None
df['avg_sell_quantity'] = None
df.loc[df['is_buyer_maker'] == True, 'avg_buy_quantity'] = df[df['is_buyer_maker'] == True]['quantity'].ewm(alpha=alpha).mean()
df.loc[df['is_buyer_maker'] == False, 'avg_sell_quantity'] = df[df['is_buyer_maker'] == False]['quantity'].ewm(alpha=alpha).mean()

df['avg_buy_quantity'] = df['avg_buy_quantity'].fillna(method='ffill')
df['avg_sell_quantity'] = df['avg_sell_quantity'].fillna(method='ffill')
df['avg_buy_interval'] = df['avg_buy_interval'].fillna(method='ffill')
df['avg_sell_interval'] = df['avg_sell_interval'].fillna(method='ffill')

df['avg_buy_rate'] = 1000 / df['avg_buy_interval']
df['avg_sell_rate'] =1000 / df['avg_sell_interval']

df['avg_buy_volume'] = df['avg_buy_rate']*df['avg_buy_quantity']
df['avg_sell_volume'] = df['avg_sell_rate']*df['avg_sell_quantity']

df['I'] = (df['bid_0_quantity']- df['ask_0_quantity']) / (df['bid_0_quantity'] + df['ask_0_quantity'])
df['OI'] = (df['avg_buy_rate']-df['avg_sell_rate']) / (df['avg_buy_rate'] + df['avg_sell_rate'])
df['QI'] = (df['avg_buy_quantity']-df['avg_sell_quantity']) / (df['avg_buy_quantity'] + df['avg_sell_quantity'])
df['VI'] = (df['avg_buy_volume']-df['avg_sell_volume']) / (df['avg_buy_volume'] + df['avg_sell_volume'])

bins = np.linspace(-1, 1, 50)
df['VI_bins'] = pd.cut(df['VI'], bins, labels=bins[1:])
plt.plot(df.groupby('VI_bins')['change'].mean());
plt.grid(True)

df['adjust_mid_price'] = df['mid_price'] + df['spread']*df['I']/2
df['adjust_mid_price_9'] = df['mid_price'] + df['spread']*(-df['OI'])*2
df['adjust_mid_price_10'] = df['mid_price'] + df['spread']*(-df['VI'])*1.4

print('调整后的mid_price   的误差：', ((df['price']-df['adjust_mid_price'])**2).sum())
print('调整后的mid_price_9 的误差：', ((df['price']-df['adjust_mid_price_9'])**2).sum())
print('调整后的mid_price_10的误差：', ((df['price']-df['adjust_mid_price_10'])**2).sum())

调整后的mid_price   的误差： 0.0048373440193987035
调整后的mid_price_9 的误差： 0.004629586542840461
调整后的mid_price_10的误差： 0.004401790287167206

Prix ​​médian global

Étant donné que les commandes en attente et les données de transaction sont utiles pour prédire le prix moyen, ces deux paramètres peuvent être combinés. L’attribution de pondération ici est arbitraire et ne prend pas en compte les conditions limites. Dans les cas extrêmes, le prix moyen prédit peut être supérieur à celui prévu. entre acheter un et vendre un, mais tant que l’erreur peut être réduite, ces détails n’ont pas d’importance.

Finalement, l’erreur de prédiction est passée de 0,00487 à 0,0043. Nous n’entrerons pas dans les détails ici. Il reste encore beaucoup à explorer sur le prix moyen. Après tout, prédire le prix moyen revient à prédire le prix. Vous pouvez l’essayer vous-même .

#注意VI需要延后一个使用
df['price_change'] = np.log(df['price']/df['price'].rolling(40).mean())
df['CI'] = -1.5*df['VI'].shift()+0.7*(0.7*df['I']+0.2*df['I_2']+0.1*df['I_3'])**3 + 150*df['price_change'].shift(1)

df['adjust_mid_price_11'] = df['mid_price'] + df['spread']*(df['CI'])
print('调整后的mid_price_11的误差：', ((df['price']-df['adjust_mid_price_11'])**2).sum())

调整后的mid_price_11的误差： 0.00421125960463469

Résumer

Cet article combine des données de profondeur et des données de transaction pour améliorer encore la méthode de calcul du prix moyen. Cet article fournit une méthode pour mesurer la précision et améliorer la précision des prévisions de changement de prix. Globalement, les différents paramètres ne sont pas très rigoureux et sont à titre indicatif. Avec un prix moyen plus précis, l’étape suivante consiste à appliquer réellement le prix moyen pour le backtesting. Cette partie comporte également beaucoup de contenu, nous arrêterons donc de mettre à jour pendant un certain temps.