Réflexions sur les stratégies de négociation à haute fréquence (4)

L'article précédent a démontré la nécessité d'ajuster dynamiquement les paramètres et comment évaluer la qualité des estimations en étudiant les intervalles d'arrivée des commandes.

Données de profondeur

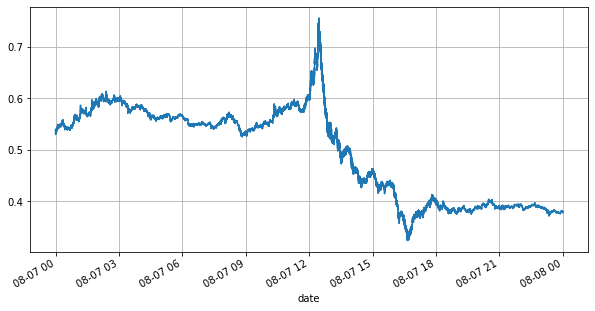
Binance fournit des téléchargements de données historiques pour best_bid_price (le prix d'achat le plus élevé), best_bid_quantity (la quantité au meilleur prix d'achat), best_ask_price (le prix de vente le plus bas), best_ask_quantity (la quantité au meilleur prix d'achat) et transaction_time. Ces données n'incluent pas les niveaux de carnet de commandes de deuxième ou plus profond. L'analyse dans cet article est basée sur le marché YGG le 7 août, qui a connu une volatilité significative avec plus de 9 millions de points de données.

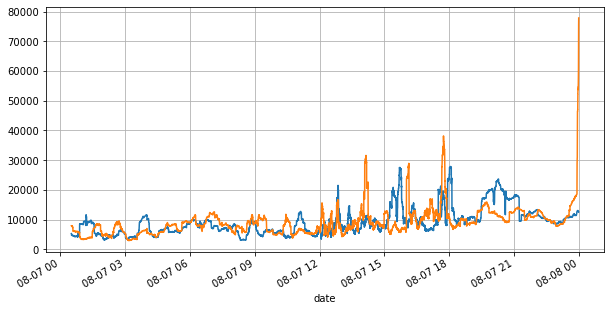
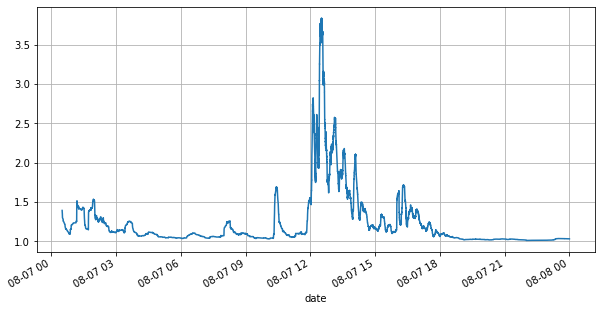
Dans le même temps, le volume des commandes changeait considérablement avec la volatilité du marché. Le spread, en particulier, indiquait l'étendue des fluctuations du marché, qui est la différence entre les meilleurs prix d'achat et d'achat. Dans les statistiques du marché YGG ce jour-là, le spread était supérieur à un tick pour 20% du temps. Dans cette ère de différents robots de trading en compétition dans le livre de commandes, de telles situations deviennent de plus en plus rares.

Dans [1]:

from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

Dans [2]:

books = pd.read_csv('YGGUSDT-bookTicker-2023-08-07.csv')

Dans [3]:

tick_size = 0.0001

Dans [4]:

books['date'] = pd.to_datetime(books['transaction_time'], unit='ms')
books.index = books['date']

Dans [5]:

books['spread'] = round(books['best_ask_price'] - books['best_bid_price'],4)

Dans [6]:

books['best_bid_price'][::10].plot(figsize=(10,5),grid=True);

Extrait [6]:

Dans [7]:

books['best_bid_qty'][::10].rolling(10000).mean().plot(figsize=(10,5),grid=True);
books['best_ask_qty'][::10].rolling(10000).mean().plot(figsize=(10,5),grid=True);

À l'extérieur[7]:

Dans [8]:

(books['spread'][::10]/tick_size).rolling(10000).mean().plot(figsize=(10,5),grid=True);

À l'extérieur[8]:

Dans [9]:

books['spread'].value_counts()[books['spread'].value_counts()>500]/books['spread'].value_counts().sum()

À l'extérieur[9]:

Citations déséquilibrées

Les cotations déséquilibrées sont observées à partir de la différence significative dans le volume du carnet d'ordres entre les ordres d'achat et de vente la plupart du temps. Cette différence a un fort effet prédictif sur les tendances à court terme du marché, similaire à la raison mentionnée précédemment qu'une diminution du volume des ordres d'achat conduit souvent à un déclin. Si un côté du carnet d'ordres est significativement plus petit que l'autre, en supposant que les ordres d'achat et de vente actifs sont similaires en volume, il y a une plus grande probabilité que le côté plus petit soit consommé, entraînant ainsi des changements de prix.

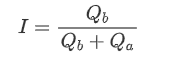
où Q_b représente le montant des ordres d' achat en attente (best_bid_qty) et Q_a représente le montant des ordres de vente en attente (best_ask_qty).

Définir le prix moyen:

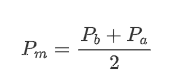
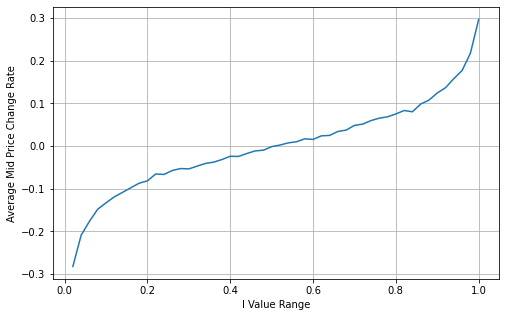
Le graphique ci-dessous montre la relation entre le taux de variation du prix moyen sur l'intervalle 1 suivant et le déséquilibre I. Comme prévu, plus le prix est susceptible d'augmenter à mesure que I augmente et plus il se rapproche de 1, plus le changement de prix s'accélère. Dans le trading à haute fréquence, l'introduction du prix intermédiaire est de mieux prédire les changements de prix futurs, c'est-à-dire que la différence de prix future est plus petite, mieux le prix intermédiaire est défini.

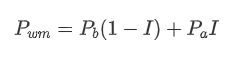
Dans [10]:

books['I'] = books['best_bid_qty'] / (books['best_bid_qty'] + books['best_ask_qty'])

Dans [11]:

books['mid_price'] = (books['best_ask_price'] + books['best_bid_price'])/2

Dans [12]:

bins = np.linspace(0, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['price_change'] = (books['mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['price_change'].mean()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Average Mid Price Change Rate');
plt.grid(True)

À l'extérieur [12]:

Dans [13]:

books['weighted_mid_price'] = books['mid_price'] + books['spread']*books['I']/2
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['weighted_price_change'] = (books['weighted_mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['weighted_price_change'].mean()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

À l'extérieur[13]:

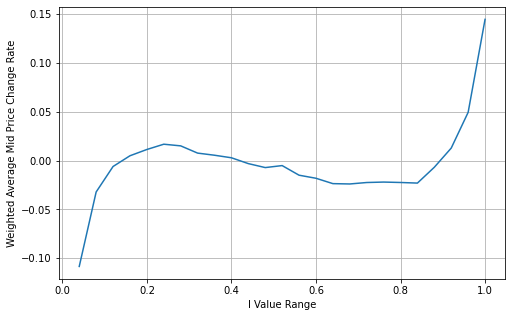
Prix moyen pondéré ajusté:

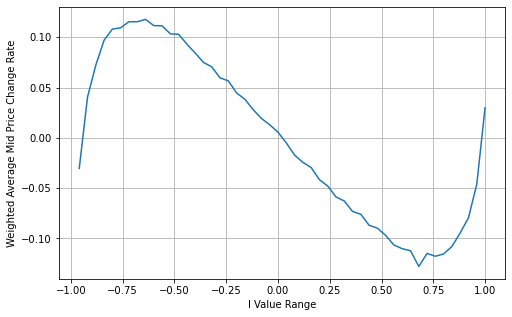
Le graphique montre que le prix moyen pondéré montre de plus petites variations par rapport aux différentes valeurs de I, ce qui indique qu'il convient mieux. Cependant, il y a encore quelques écarts, en particulier autour de 0,2 et 0,8. Cela suggère que je fournis encore des informations supplémentaires. L'hypothèse d'une relation complètement linéaire entre le terme de correction de prix et I, comme l'implique le prix moyen pondéré, ne correspond pas à la réalité. On peut voir sur le graphique que la vitesse d'écart augmente lorsque je m'approche de 0 et 1, ce qui indique une relation non linéaire.

Pour fournir une représentation plus intuitive, voici une redéfinition de I:

Définition révisée de I:

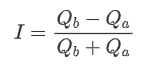
À ce stade:

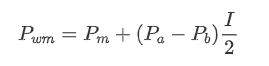
En observant, on peut remarquer que le prix moyen pondéré est une correction du prix moyen moyen, où le terme de correction est multiplié par l'écart. Le terme de correction est une fonction de I, et le prix moyen pondéré suppose une relation simple de I/2. Dans ce cas, l'avantage de la distribution I ajustée (-1, 1) devient évident, car I est symétrique autour de l'origine, ce qui permet de trouver une relation appropriée pour la fonction. En examinant le graphique, il semble que cette fonction devrait satisfaire les puissances de I, car elle s'aligne sur la croissance rapide des deux côtés et la symétrie de l'origine. En outre, on peut observer que les valeurs proches de l'origine sont proches de linéaire.

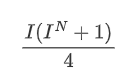
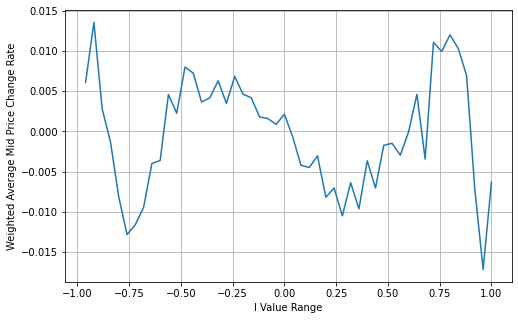
Ici, N est un nombre pair positif, après les tests réels, il est préférable que N soit 8.

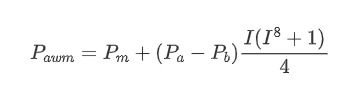
À ce stade, la prédiction des changements de prix moyens n'est plus significativement liée à I. Bien que ce résultat soit légèrement meilleur que le simple prix moyen pondéré, il n'est toujours pas applicable dans les scénarios de négociation réels.Le micro-prixLes chercheurs peuvent explorer cette approche plus en détail.

Dans [14]:

books['I'] = (books['best_bid_qty'] - books['best_ask_qty']) / (books['best_bid_qty'] + books['best_ask_qty'])

Dans [15]:

books['weighted_mid_price'] = books['mid_price'] + books['spread']*books['I']/2
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['weighted_price_change'] = (books['weighted_mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['weighted_price_change'].mean()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

Extrait [1]:

Dans [16]:

books['adjust_mid_price'] = books['mid_price'] + books['spread']*books['I']*(books['I']**8+1)/4
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['adjust_mid_price'] = (books['adjust_mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['adjust_mid_price'].mean()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

Extrait [1]:

Résumé

Le prix moyen est crucial pour les stratégies à haute fréquence car il sert de prédiction des prix futurs à court terme. Par conséquent, il est important que le prix moyen soit aussi précis que possible. Les approches de prix moyens discutées précédemment sont basées sur les données du carnet d'ordres, car seul le niveau supérieur du carnet d'ordres est utilisé dans l'analyse. Dans le trading en direct, les stratégies devraient viser à utiliser toutes les données disponibles, y compris les données commerciales, pour valider les prédictions de prix moyens par rapport aux prix de transaction réels.

Plus de