मोंटे कार्लो एल्गोरिथ्मः अल्फ़ा डॉग की चालाकी, इसे देखने के बाद समझ में आता है!

इस साल 9 से 15 मार्च तक, गोओ के लिए एक बड़ी घटना हुई, जिसमें दक्षिण कोरिया के सियोल में पांच राउंड की मानव-मशीन लड़ाई हुई। इस खेल का नतीजा यह हुआ कि मानव को हार का सामना करना पड़ा और विश्व गो चैंपियन ली शिजी ने गूगल के आर्टिफिशियल इंटेलिजेंस प्रोग्राम अल्फागो को 1-4 से हराया। तो, अल्फागो क्या है, और जीतने के लिए कुंजी कहाँ है? यहाँ हम एक एल्गोरिथ्म के बारे में बात करने जा रहे हैं: मोंटे कार्लो एल्गोरिथ्म

• ### अल्फागो और मोंटे कार्लो एल्गोरिदम

समाचार एजेंसी सिन्हुआ की रिपोर्ट के अनुसार, अल्फागो प्रोग्राम एक मानव-मशीन गोवा गेम है जिसे अमेरिकी कंपनी गूगल की डीपमाइंड टीम द्वारा विकसित किया गया है, जिसे चीनी शतरंज प्रशंसकों द्वारा “अल्फा कुत्ता” के रूप में जाना जाता है।

पिछले लेख में, हमने Google द्वारा विकसित किए जा रहे तंत्रिका नेटवर्क एल्गोरिदम के बारे में बात की थी, जो मशीनों को स्वायत्त रूप से सीखने के लिए डिज़ाइन किया गया है, और अल्फागो भी इसी तरह का एक उत्पाद है।

चीनी ऑटोमेशन एसोसिएशन के उपाध्यक्ष और सचिव वांग फ्लिप ने कहा कि प्रोग्रामर को गोओ में महारत हासिल करने की जरूरत नहीं है, उन्हें केवल गोओ के बुनियादी नियमों को जानने की जरूरत है। अल्फागो के पीछे एक उत्कृष्ट कंप्यूटर वैज्ञानिकों का समूह है, जो मशीन सीखने के क्षेत्र में विशेषज्ञ हैं। वैज्ञानिकों ने तंत्रिका नेटवर्क एल्गोरिदम का उपयोग करते हुए, कंप्यूटर में शतरंज विशेषज्ञों के खेल रिकॉर्ड दर्ज किए हैं, और कंप्यूटर को खुद के साथ खेलते हैं, इस प्रक्रिया में लगातार प्रशिक्षण प्राप्त करते हैं। एक तरह से, यह कहा जा सकता है कि अल्फागो की शतरंज कौशल को डेवलपर द्वारा सिखाया नहीं गया था, बल्कि आत्म-सिखाया गया था।

तो, अल्फागो को प्रतिभाशाली बनाने के लिए कौन सी कुंजी है? यह मोंटे कार्लो एल्गोरिथ्म है।

मोंटे कार्लो एल्गोरिथ्म क्या है? हम आम तौर पर मोंटे कार्लो एल्गोरिथ्म की व्याख्या करते हैंः यदि एक बास्केट में 1,000 सेब हैं, तो आप अपनी आँखें बंद करके हर बार सबसे बड़े सेब को चुन सकते हैं, और आप चुनने की कोई सीमा नहीं रखते हैं। तो आप अपनी आँखें बंद करके एक को यादृच्छिक रूप से ले सकते हैं, फिर एक को यादृच्छिक रूप से पहले के साथ तुलना कर सकते हैं, एक बड़ा छोड़ सकते हैं, फिर एक और यादृच्छिक रूप से ले सकते हैं, और फिर एक बड़ा छोड़ सकते हैं। यह चक्र बार-बार होता है, और जितनी बार आप सबसे बड़ा सेब चुनते हैं, उतनी ही अधिक संभावना है, लेकिन जब तक आप सभी 1,000 सेबों को एक बार नहीं चुनते, तब तक आप निश्चित रूप से सबसे बड़ा नहीं चुन सकते।

यह कहना है कि मोंटे कार्लो एल्गोरिथ्म है कि जितना अधिक नमूने हैं, उतना ही सबसे अच्छा समाधान है, लेकिन यह सबसे अच्छा होने की गारंटी नहीं है, क्योंकि यदि 10,000 सेब हैं, तो शायद एक बड़ा मिल जाएगा।

और यह एक ऐसी चीज है जिसके बारे में आप सोच सकते हैं कि वेगास के एल्गोरिदम के साथ तुलना की जा सकती हैः आम तौर पर कहा जाता है कि यदि एक ताला है, तो 1000 चाबियाँ हैं, लेकिन केवल एक ही सही है। इसलिए हर बार जब आप यादृच्छिक रूप से एक चाबी लेते हैं और कोशिश करते हैं, तो इसे खोलने में विफल रहते हैं, तो इसे बदल दें। जितनी बार कोशिश की जाती है, सबसे अच्छा समाधान खोलने की संभावना उतनी ही अधिक होती है, लेकिन खोलने से पहले, गलत चाबियाँ बेकार हैं।

तो लास वेगास एल्गोरिथ्म सबसे अच्छा संभव समाधान है, लेकिन जरूरी नहीं कि यह मिल सके। मान लीजिए कि 1000 कुंजी में से कोई भी ताला खोलने के लिए कुंजी नहीं है, असली कुंजी 1001 है, लेकिन नमूने में 1001 एल्गोरिथ्म नहीं है, लास वेगास एल्गोरिथ्म ताला खोलने के लिए कुंजी नहीं ढूंढ सकता है।

अल्फागो का मोंटे कार्लो एल्गोरिदम गोआ की कठिनाई एआई के लिए विशेष रूप से बड़ी है, क्योंकि गोआ में कई प्रकार के पत्ते हैं जिन्हें कंप्यूटर के लिए अलग करना मुश्किल है। वांग फिसिंग ने कहाः सबसे पहले, गोओ में बहुत अधिक संभावनाएं हैं। गोओ के प्रत्येक चरण में बहुत अधिक संभावित निर्णय हैं, जब खिलाड़ी शुरू होता है तो उसके पास 19 × 19 = 361 ड्रॉ विकल्प होते हैं। एक खेल में 150 राउंड के गोओ में 10170 से अधिक स्थितियां हो सकती हैं। दूसरा, नियम बहुत नाजुक है, कुछ हद तक ड्रॉ विकल्प अनुभव संचय से बने अंतर्ज्ञान पर निर्भर करता है। इसके अलावा, गोओ के शतरंज में, कंप्यूटर को वर्तमान शतरंज के फायदे और कमजोरियों को अलग करना मुश्किल है। इसलिए, गोओ चुनौती को एआई की अपोलो योजना कहा जाता है।

अल्फागो सिर्फ एक मोंटे कार्लो एल्गोरिथ्म नहीं है, बल्कि यह मोंटे कार्लो एल्गोरिथ्म का एक उन्नत संस्करण है।

अल्फागो ने मोंटे कार्लो ट्री सर्च एल्गोरिदम और दो गहरे तंत्रिका नेटवर्क के साथ मिलकर शतरंज खेला। ली सेठ के साथ मुकाबले से पहले, गूगल ने पहले अल्फागो कुत्ता के तंत्रिका नेटवर्क को लगभग 30 मिलियन पैदल चलने वाले मानव जोड़े के साथ प्रशिक्षित किया, ताकि यह सीख सके कि मानव पेशेवर शतरंजियों को कैसे गिराया जाए। इसके बाद, अल्फागो को खुद को शतरंज खेलने दें, जिससे बड़े पैमाने पर एक नया शतरंज बना सके। गूगल इंजीनियरों ने घोषणा की कि अल्फागो प्रति दिन लाखों पैदल चलने की कोशिश कर सकता है।

उनके काम में यह शामिल है कि वे एक दूसरे के साथ काम करें और सबसे आशाजनक चालों को चुनें, और स्पष्ट रूप से खराब चालों को छोड़ दें, जिससे गणना को नियंत्रित किया जा सके जो कंप्यूटर कर सकता है। मूल रूप से, यह वही है जो मानव शतरंज खिलाड़ी करते हैं।

चीनी विज्ञान अकादमी के स्वचालन अनुसंधान संस्थान के एक शोधकर्ता इयांग यांग ने कहा कि पारंपरिक शतरंज सॉफ़्टवेयर, आमतौर पर गहरे नीले कंप्यूटर सहित हिंसक खोज का उपयोग करता है, जो सभी संभावित परिणामों के लिए एक खोज पेड़ बनाता है (प्रत्येक परिणाम पेड़ पर एक फल है), जो आवश्यकतानुसार खोज करता है। यह विधि शतरंज, पहेली और अन्य के लिए भी संभव है, लेकिन गोवा के लिए यह संभव नहीं है, क्योंकि गोवा प्रत्येक 19 लाइनों को पार करता है, ड्रॉप्स की संभावना इतनी अधिक है कि कंप्यूटर इस पेड़ का निर्माण नहीं कर सकता है (फल बहुत अधिक है) क्रॉस-सर्च को पूरा करने के लिए। और अल्फागो ने एक बहुत ही स्मार्ट तरीका अपनाया है। यह गहरी सीखने की विधि का उपयोग करके खोज की जटिलता को कम करता है, और खोज स्थान को कम करने के लिए प्रभावी है। उदाहरण के लिए, रणनीति नेटवर्क कंप्यूटर को खोज करने के लिए निर्देशित करता है जो मानव हाथ की तरह अधिक है।

डोगाची ने आगे समझाया कि डीपीएन की सबसे बुनियादी इकाई हमारे मानव मस्तिष्क के न्यूरॉन्स की तरह है, कई परतों से जुड़ा हुआ है जैसे कि यह मानव मस्तिष्क का एक तंत्रिका नेटवर्क है। अल्फागो के दो तंत्रिका नेटवर्क, रणनीति नेटवर्क और मूल्यांकन नेटवर्क हैं।

पहेली रणनीति नेटवर्क मुख्य रूप से गिरने की रणनीति उत्पन्न करने के लिए उपयोग किया जाता है। शतरंज खेलने की प्रक्रिया में, यह विचार नहीं करता है कि उसे क्या करना चाहिए, लेकिन यह सोचता है कि मानव हाथ क्या होगा। यही है, यह इनपुट पट्टिका की वर्तमान स्थिति के आधार पर भविष्यवाणी करेगा कि मानव अगला शतरंज कहां होगा, और मानव सोच के अनुरूप सबसे अधिक व्यवहार्य विकल्पों की पेशकश करेगा।

हालांकि, रणनीतिक नेटवर्क को यह नहीं पता है कि यह कदम कितना अच्छा है, यह केवल यह जानता है कि क्या यह कदम मानव के समान है, और तब मूल्यांकन नेटवर्क को काम करने की आवश्यकता होती है।

डेंगॉग ने कहाः “नीलामी नेटवर्क सभी संभावित विकल्पों के लिए पूरे डिप्लोमा की स्थिति का मूल्यांकन करता है, और फिर एक जीत की दर देता है। ये मान मोंटे कार्लो ट्री सर्च एल्गोरिथ्म में प्रतिबिंबित होते हैं, जो इस प्रक्रिया को दोहराकर सबसे अधिक जीत की दर वाले कदम को पेश करते हैं। मोंटे कार्लो ट्री सर्च एल्गोरिथ्म ने तय किया कि रणनीति नेटवर्क केवल उन स्थानों पर जारी रहेगा जहां जीत की दर अधिक है, ताकि कुछ मार्गों को छोड़ दिया जा सके, बिना किसी मार्ग के काले को गिनने के लिए।

अल्फागो इन दोनों उपकरणों का उपयोग स्थिति का विश्लेषण करने के लिए करता है और प्रत्येक रणनीति के लिए अच्छाई और बुराई का आकलन करता है, जैसे कि एक मानव शतरंज खिलाड़ी वर्तमान स्थिति का आकलन करेगा और भविष्य की स्थिति का अनुमान लगाएगा। मोंटे कार्लो ट्री सर्च एल्गोरिथ्म का उपयोग करके विश्लेषण किया गया है, उदाहरण के लिए, अगले 20 चरणों के मामले में, यह निर्धारित किया जा सकता है कि किस स्थिति में जीतने की संभावना अधिक होगी।

लेकिन इसमें कोई संदेह नहीं है कि मोंटे कार्लो एल्गोरिथ्म अल्फागो के मूल में से एक है।

दो छोटे प्रयोग अंत में, मोंटे कार्लो एल्गोरिथ्म के दो छोटे प्रयोगों पर एक नज़र डालें।

• ### 1. परिधि की गणना करें

सिद्धांत: पहले एक वर्ग खींचें, उसके अंदर से एक वृत्त खींचें, और फिर उस वर्ग के अंदर एक यादृच्छिक बिंदु खींचें, और उस बिंदु को वृत्त के अंदर P के रूप में सेट करें, तो P = वृत्त क्षेत्रफल / वर्ग क्षेत्रफल। P=(Pi*R*R)/(2R*2R) = Pi/4, यानि Pi=4P

कदम: 1. मूल बिंदु पर गोलाकार केंद्र रखें, आर को त्रिज्या के रूप में गोलाकार करें, और पहले चतुर्भुज का ¹⁄₄ गोलाकार क्षेत्र Pi है*R*R/4 2. एक चौथाई परिधि के बाहरी चौकोर के रूप में कार्य करें, निर्देशांक है, तो यह चौकोर के क्षेत्रफल R है*R 3. तुरंत बिंदुओं को ले लो (X, Y), ताकि 0 <= X <= R और 0 <= Y <= R, यानी बिंदु वर्ग के भीतर है 4. सूत्र X के द्वारा*X+Y*Y*क्या R का निर्णय बिंदु ¹⁄₄ परिधि के भीतर है? 5. सभी बिंदुओं की संख्या (यानी प्रयोगों की संख्या) N है, और ¹⁄₄ वृत्त के भीतर स्थित बिंदुओं की संख्या (यानी चरण 4 के बिंदुओं को पूरा करने वाले बिंदुओं की संख्या) M है, तो

P=M/N तो Pi=4*N/M चित्र 1

M_C{10000} का परिणाम 3.1424 है

• ### 2. मोंटे कार्लो के अनुकरण के लिए फ़ंक्शन के चरम मान, स्थानीय चरम मानों में फंसने से बचें

# अंतराल में[-2,2] पर एक संख्या को यादृच्छिक रूप से उत्पन्न करें, उसके अनुरूप y को खोजें, और सबसे बड़ा मान लें कि फलन में[-2,2] पर अधिकतम मान 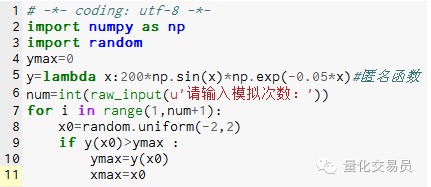चित्र 2

सिमुलेशन 1000 बार के बाद 185.12292832389875 (बहुत सटीक) का अधिकतम मूल्य पाया गया

यहाँ, आप समझ गए होंगे कोड को हाथ से लिखा जा सकता है, बहुत मजेदार है! WeChat के पब्लिक नंबर से पुनर्प्रकाशित