उच्च आवृत्ति ट्रेडिंग रणनीतियों पर विचार (1)
 3
3
 4856
4856

लेख में डिजिटल मुद्राओं की उच्च आवृत्ति व्यापार रणनीतियों पर चर्चा की गई है, जिसमें लाभ के स्रोत (मुख्य रूप से बाजार में उतार-चढ़ाव और विनिमय शुल्क छूट से), ऑर्डर प्लेसमेंट और स्थिति नियंत्रण के मुद्दे, और पेरेटो वितरण का उपयोग करके ट्रेडिंग वॉल्यूम मॉडलिंग की विधि शामिल है। इसके अलावा, बायनेन्स द्वारा प्रदान किए गए लेनदेन और इष्टतम ऑर्डर डेटा का उपयोग बैकटेस्टिंग के लिए किया गया था, और उच्च आवृत्ति ट्रेडिंग रणनीतियों के अन्य मुद्दों पर बाद के लेखों में गहराई से चर्चा करने की योजना है।
मैंने पहले भी डिजिटल मुद्राओं के उच्च आवृत्ति व्यापार के बारे में दो लेख लिखे हैं। डिजिटल मुद्राओं के लिए उच्च आवृत्ति रणनीतियों का विस्तृत परिचय, 5 दिनों में 80 गुना कमाएँ, उच्च आवृत्ति रणनीति की शक्ति. लेकिन इसे केवल अनुभव साझा करना और सामान्य बातचीत ही माना जा सकता है। इस बार मैं शुरू से ही हाई-फ़्रीक्वेंसी ट्रेडिंग के विचारों को पेश करने के लिए लेखों की एक श्रृंखला लिखने की योजना बना रहा हूँ। मुझे उम्मीद है कि मैं यथासंभव संक्षिप्त और स्पष्ट रहूँगा। हालाँकि, हाई-फ़्रीक्वेंसी के बारे में मेरी सीमित स्तर और गहन समझ के कारण ट्रेडिंग के बारे में यह लेख सिर्फ़ एक शुरुआती बिंदु है। मुझे उम्मीद है कि विशेषज्ञ मुझे सही कर सकते हैं।
उच्च आवृत्ति लाभ स्रोत
जैसा कि पिछले लेखों में बताया गया है, उच्च आवृत्ति वाली रणनीतियाँ विशेष रूप से अत्यधिक अस्थिर उतार-चढ़ाव वाले बाजारों के लिए उपयुक्त हैं। किसी व्यापारिक उत्पाद के मूल्य में अल्प समय में होने वाले परिवर्तनों की जांच करें, जिसमें समग्र रुझान और उतार-चढ़ाव शामिल हों। अगर हम रुझानों में होने वाले बदलावों का सटीक अनुमान लगा सकते हैं, तो हम निश्चित रूप से पैसा कमा सकते हैं, लेकिन यह सबसे कठिन भी है। यह लेख मुख्य रूप से उच्च आवृत्ति निर्माता रणनीतियों का परिचय देता है और इस मुद्दे को शामिल नहीं करेगा। अस्थिर बाजार में, यदि ऑर्डर को ऊपर-नीचे रखने की रणनीति को बार-बार क्रियान्वित किया जाता है और लाभ मार्जिन काफी बड़ा है, तो यह प्रवृत्ति के कारण होने वाले संभावित नुकसान को कवर कर सकता है, जिससे आप बाजार की भविष्यवाणी किए बिना लाभ कमा सकते हैं। वर्तमान में, एक्सचेंजों पर सभी मेकर लेनदेन को लेनदेन शुल्क पर छूट मिलती है, जो लाभ का एक घटक भी है। प्रतिस्पर्धा जितनी तीव्र होगी, छूट का अनुपात उतना ही अधिक होना चाहिए।
समस्या का समाधान किया जाना है
यह रणनीति एक ही समय में खरीद और बिक्री के ऑर्डर देती है। पहला सवाल यह है कि ऑर्डर कहां दिए जाएं। ऑर्डर बाज़ार के जितना करीब होगा, लेन-देन की संभावना उतनी ही ज़्यादा होगी। हालाँकि, अस्थिर बाज़ार में, तात्कालिक लेन-देन मूल्य बाज़ार से बहुत दूर हो सकता है। अगर ऑर्डर बहुत नज़दीक रखा गया है, तो आप ऐसा नहीं कर पाएँगे। पर्याप्त लाभ प्राप्त करें. बहुत दूर दिए गए ऑर्डर के निष्पादन की संभावना कम है। यह एक ऐसी समस्या है जिसका अनुकूलन किया जाना आवश्यक है।
अपनी स्थिति पर नियंत्रण रखें. जोखिमों को नियंत्रित करने के लिए, रणनीति में लंबे समय तक बहुत अधिक पदों को संचित नहीं किया जा सकता है। इसे ऑर्डर दूरी, ऑर्डर मात्रा, कुल स्थिति सीमा आदि को नियंत्रित करके हल किया जा सकता है।
उपरोक्त लक्ष्यों को प्राप्त करने के लिए, लेन-देन की संभावना, लेन-देन लाभ, बाजार अनुमान और अन्य पहलुओं का मॉडल बनाना और अनुमान लगाना आवश्यक है। इस क्षेत्र में कई लेख और पेपर हैं, जिन्हें हाई-फ़्रीक्वेंसी ट्रेडिंग जैसे कीवर्ड के साथ पाया जा सकता है , ऑर्डरबुक, आदि. ऑनलाइन कई सिफारिशें हैं, जिनके बारे में मैं यहां नहीं बताऊंगा। इसके अलावा, एक विश्वसनीय और तेज़ बैकटेस्टिंग सिस्टम स्थापित करना सबसे अच्छा है। हालाँकि उच्च-आवृत्ति रणनीतियों को उनकी प्रभावशीलता को सत्यापित करने के लिए वास्तविक ट्रेडिंग के माध्यम से आसानी से सत्यापित किया जा सकता है, बैकटेस्टिंग अभी भी अधिक विचार प्रदान कर सकता है और परीक्षण और त्रुटि की लागत को कम कर सकता है।
आवश्यक डेटा
Binance लेनदेन-दर-लेनदेन और सर्वोत्तम ऑर्डर डेटा प्रदान करता हैडाउनलोड करनाडीप डेटा को श्वेतसूची में एपीआई का उपयोग करके डाउनलोड किया जाना चाहिए, या आप इसे स्वयं एकत्र कर सकते हैं। बैकटेस्टिंग प्रयोजनों के लिए, आप केवल एकत्रित लेनदेन डेटा का उपयोग कर सकते हैं। यह आलेख HOOKUSDT-aggTrades-2023-01-27 के डेटा को उदाहरण के रूप में लेता है।
from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
लेन-देन कॉलम इस प्रकार हैं:
- agg_trade_id: एकत्रित लेनदेन आदेश की आईडी,
- मूल्य: लेनदेन मूल्य
- मात्रा: लेन-देन की संख्या
- first_trade_id: संग्रह में एक ही समय में कई लेनदेन हो सकते हैं, केवल एक डेटा की गणना की जाती है, यह पहले लेनदेन की आईडी है
- last_trade_id: अंतिम लेनदेन की आईडी
- transact_time: लेनदेन का समय
- is_buyer_maker: लेन-देन की दिशा, सत्य का अर्थ है कि खरीद आदेश निर्माता द्वारा कारोबार किया जाता है, और बिक्री आदेश लेने वाले द्वारा कारोबार किया जाता है
यह देखा जा सकता है कि उस दिन 660,000 लेनदेन डेटा थे, और लेनदेन बहुत सक्रिय थे। सीएसवी टिप्पणी अनुभाग में संलग्न किया जाएगा।
trades = pd.read_csv('COMPUSDT-aggTrades-2023-07-02.csv')
trades
664475 rows × 7 columns
| agg_trade_id | price | quantity | first_trade_id | last_trade_id | transact_time | is_buyer_maker |
|---|---|---|---|---|---|---|
| 120719552 | 52.42 | 22.087 | 207862988 | 207862990 | 1688256004603 | False |
| 120719553 | 52.41 | 29.314 | 207862991 | 207863002 | 1688256004623 | True |
| 120719554 | 52.42 | 0.945 | 207863003 | 207863003 | 1688256004678 | False |
| 120719555 | 52.41 | 13.534 | 207863004 | 207863006 | 1688256004680 | True |
| … | … | … | … | … | … | … |
| 121384024 | 68.29 | 10.065 | 210364899 | 210364905 | 1688342399863 | False |
| 121384025 | 68.30 | 7.078 | 210364906 | 210364908 | 1688342399948 | False |
| 121384026 | 68.29 | 7.622 | 210364909 | 210364911 | 1688342399979 | True |
एकल लेनदेन मात्रा मॉडलिंग
सबसे पहले, डेटा को संसाधित करें और मूल ट्रेडों को खरीद आदेश सक्रिय लेनदेन समूह और बिक्री आदेश सक्रिय लेनदेन समूह में विभाजित करें। इसके अलावा, मूल एकत्रित लेनदेन डेटा एक ही समय, एक ही कीमत और एक ही दिशा में डेटा का एक टुकड़ा है। 100 का एक सक्रिय खरीद आदेश हो सकता है। यदि इसे अलग-अलग कीमतों के साथ कई लेनदेन में विभाजित किया जाता है, तो ऐसा होता है 60 और 40 के रूप में, डेटा के दो टुकड़े उत्पन्न होंगे, जो खरीद आदेश मात्रा के अनुमान को प्रभावित करेंगे। इसलिए, transact_time के आधार पर पुनः एकत्रीकरण करना आवश्यक है। एकत्रीकरण के बाद, डेटा की मात्रा 140,000 रिकॉर्ड कम हो गई।
trades['date'] = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index = trades['date']
buy_trades = trades[trades['is_buyer_maker']==False].copy()
sell_trades = trades[trades['is_buyer_maker']==True].copy()
buy_trades = buy_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
sell_trades = sell_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
buy_trades['interval']=buy_trades['transact_time'] - buy_trades['transact_time'].shift()
sell_trades['interval']=sell_trades['transact_time'] - sell_trades['transact_time'].shift()
print(trades.shape[0] - (buy_trades.shape[0]+sell_trades.shape[0]))
146181
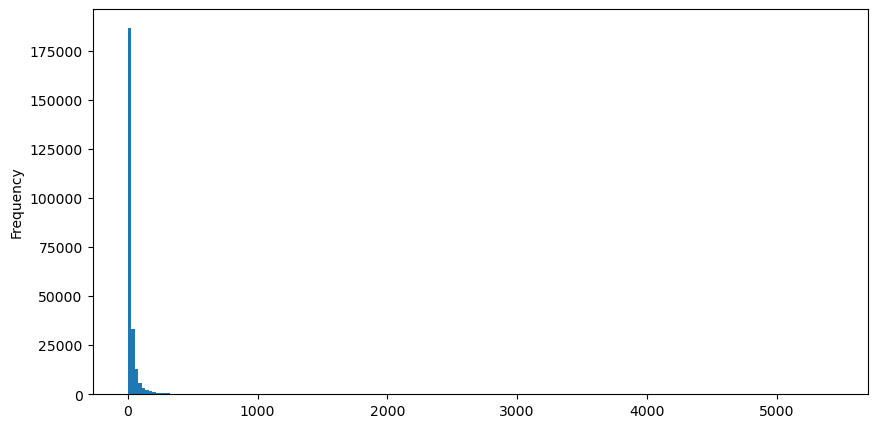
खरीद आदेशों को उदाहरण के रूप में लेते हुए, पहले एक हिस्टोग्राम बनाएं। आप देख सकते हैं कि लंबी पूंछ का प्रभाव बहुत स्पष्ट है। अधिकांश डेटा दूर बाईं ओर केंद्रित है, लेकिन पूंछ पर वितरित बड़ी संख्या में लेनदेन भी हैं .
buy_trades['quantity'].plot.hist(bins=200,figsize=(10, 5));
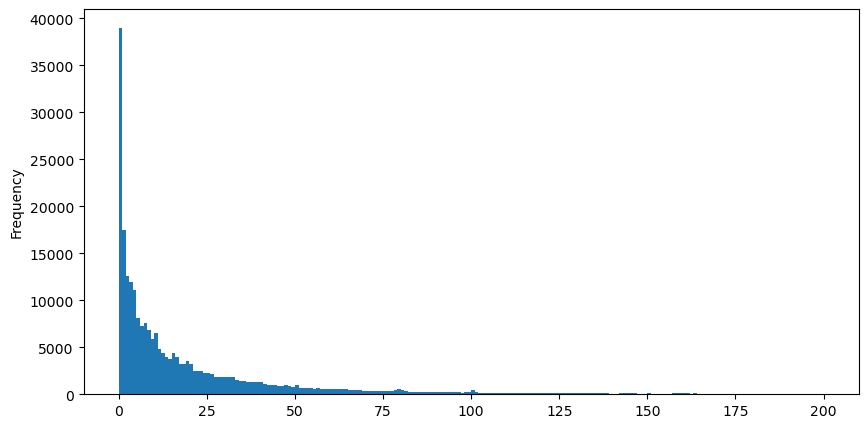
अवलोकन की सुविधा के लिए, हम पूंछ को काटते हैं और देखते हैं। हम देख सकते हैं कि व्यापार की मात्रा जितनी बड़ी होगी, घटना की आवृत्ति उतनी ही कम होगी, और कमी की प्रवृत्ति उतनी ही तेज़ होगी।
buy_trades['quantity'][buy_trades['quantity']<200].plot.hist(bins=200,figsize=(10, 5));
मात्रा संतुष्टि के वितरण पर कई अध्ययन हैं। इसके घात-कानून वितरण को पैरेटो वितरण भी कहा जाता है, जो सांख्यिकीय भौतिकी और सामाजिक विज्ञान में संभाव्यता वितरण का एक सामान्य रूप है। घात कानून वितरण में, किसी निश्चित आकार (या आवृत्ति) की घटना की संभावना उस घटना के आकार के कुछ ऋणात्मक घातांक के समानुपाती होती है। इस वितरण स्वरूप की मुख्य विशेषता यह है कि बड़ी घटनाएं (अर्थात, जो माध्य से बहुत दूर होती हैं) अन्य कई वितरणों की अपेक्षा अधिक बार घटित होती हैं। यह ट्रेडिंग वॉल्यूम वितरण की विशेषता है। पेरेटो वितरण का रूप है: P(x) = Cx^(-α). निम्नलिखित इसे प्रदर्शित करेगा।
नीचे दिया गया आंकड़ा इस संभावना को दर्शाता है कि ट्रेडिंग वॉल्यूम एक निश्चित मूल्य से अधिक है। नीली रेखा वास्तविक संभावना है, और नारंगी रेखा नकली संभावना है। यहाँ विशिष्ट मापदंडों के बारे में चिंता न करें। आप देख सकते हैं कि यह करता है पेरेटो वितरण को संतुष्ट करें। चूंकि ऑर्डर वॉल्यूम 0 से अधिक होने की संभावना 1 है, और मानकीकरण आवश्यकताओं को पूरा करने के लिए, वितरण समीकरण निम्नानुसार होना चाहिए:
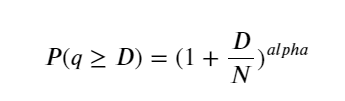
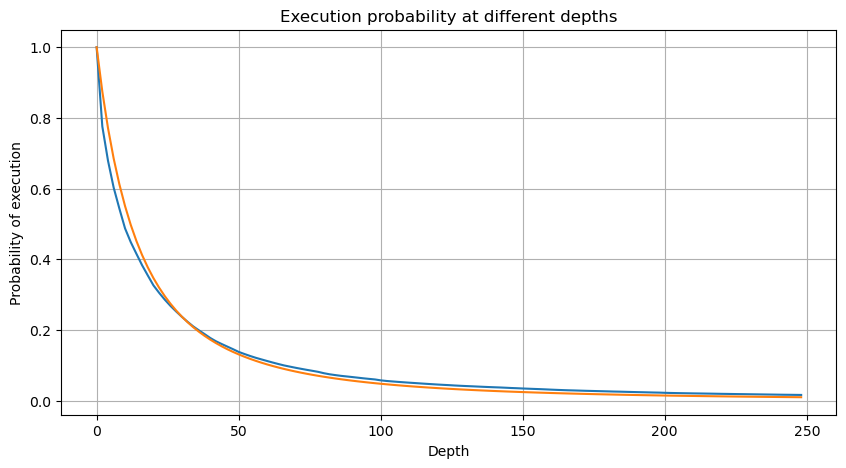
जहाँ N मानकीकृत पैरामीटर है. यहां हम औसत वॉल्यूम M और अल्फा -2.06 का चयन करते हैं। अल्फा का विशिष्ट अनुमान D=N होने पर P मान की व्युत्क्रम गणना करके निकाला जा सकता है। विशेष रूप से: अल्फा = लॉग(P(d>M))/लॉग(2)। विभिन्न बिंदुओं को चुनने से अल्फा मान में थोड़ा अंतर आएगा।
depths = range(0, 250, 2)
probabilities = np.array([np.mean(buy_trades['quantity'] > depth) for depth in depths])
alpha = np.log(np.mean(buy_trades['quantity'] > mean_quantity))/np.log(2)
mean_quantity = buy_trades['quantity'].mean()
probabilities_s = np.array([(1+depth/mean_quantity)**alpha for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)
plt.figure(figsize=(10, 5))
plt.grid(True)
plt.title('Diff')
plt.plot(depths, probabilities_s-probabilities);
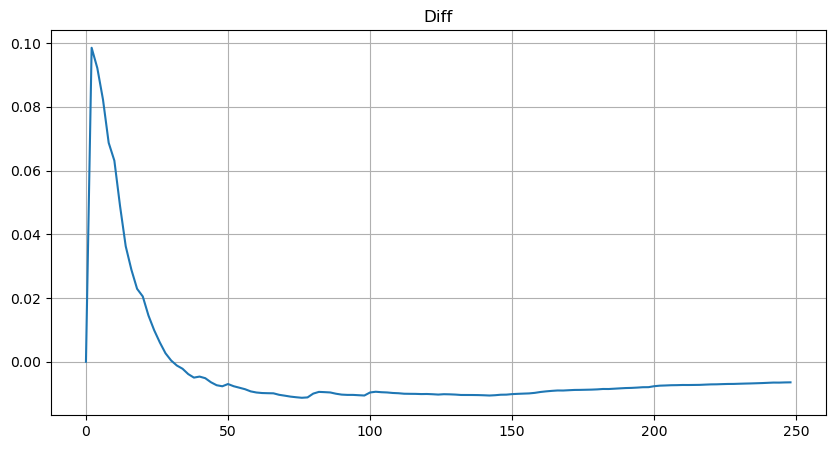
लेकिन यह अनुमान सिर्फ़ ऐसा ही लगता है। ऊपर दिए गए चित्र में, हम नकली मूल्य और वास्तविक मूल्य के बीच का अंतर दर्शाते हैं। जब ट्रेडिंग वॉल्यूम छोटा होता है, तो विचलन बड़ा होता है, यहां तक कि 10% के करीब भी। पैरामीटर आकलन के दौरान विभिन्न बिंदुओं का चयन करके किसी बिंदु की संभावना को अधिक सटीक बनाया जा सकता है, लेकिन इससे विचलन की समस्या हल नहीं होती है। यह घात-कानून वितरण और वास्तविक वितरण के बीच के अंतर से निर्धारित होता है। अधिक सटीक परिणाम प्राप्त करने के लिए, घात-कानून वितरण के समीकरण को सही करने की आवश्यकता है। मैं विशिष्ट प्रक्रिया के बारे में विस्तार से नहीं बताऊंगा, लेकिन मुझे एक प्रेरणा मिली और मैंने पाया कि यह वास्तव में इस प्रकार होना चाहिए:
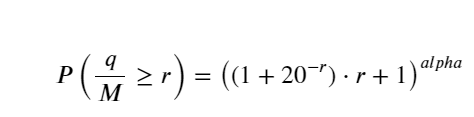
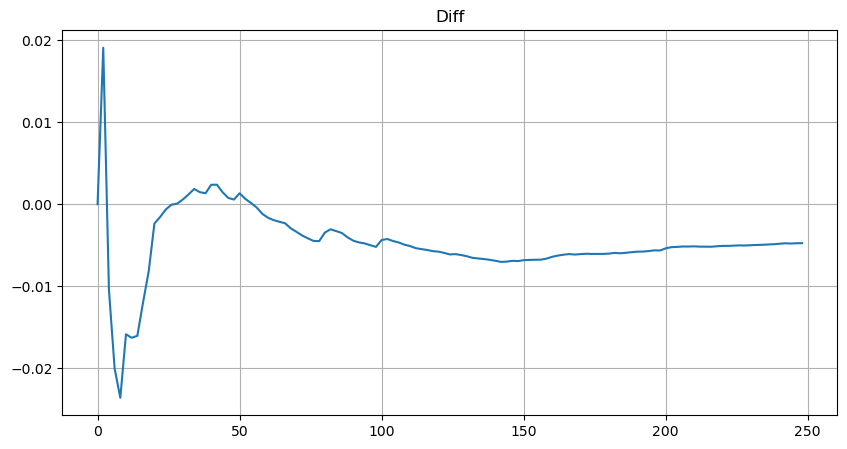
सरलता के लिए, मानकीकृत ट्रेडिंग वॉल्यूम को दर्शाने के लिए यहां r = q/M का उपयोग किया गया है। मापदंडों का अनुमान ऊपर बताए गए तरीके से ही लगाया जा सकता है। नीचे दिया गया आंकड़ा दर्शाता है कि सुधार के बाद अधिकतम विचलन 2% से अधिक नहीं है। सैद्धांतिक रूप से, सुधार जारी रखा जा सकता है, लेकिन यह सटीकता पर्याप्त है।
depths = range(0, 250, 2)
probabilities = np.array([np.mean(buy_trades['quantity'] > depth) for depth in depths])
mean = buy_trades['quantity'].mean()
alpha = np.log(np.mean(buy_trades['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([(((1+20**(-depth/mean))*depth+mean)/mean)**alpha for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)
plt.figure(figsize=(10, 5))
plt.grid(True)
plt.title('Diff')
plt.plot(depths, probabilities_s-probabilities);
आयतन वितरण के लिए अनुमानित समीकरण के साथ, ध्यान दें कि समीकरण की प्रायिकता वास्तविक प्रायिकता नहीं है, बल्कि एक सशर्त प्रायिकता है। इस बिंदु पर हम इस प्रश्न का उत्तर दे सकते हैं: यदि अगला ऑर्डर होता है, तो क्या संभावना है कि यह ऑर्डर एक निश्चित मूल्य से अधिक है? दूसरे शब्दों में, विभिन्न गहराई के आदेशों के निष्पादन की संभावना क्या है (आदर्श स्थिति, इतनी कठोर नहीं, सिद्धांत रूप में ऑर्डर बुक में नए आदेश और रद्दीकरण, साथ ही साथ एक ही गहराई पर कतारें हैं)।
यह लेख लगभग समाप्त हो चुका है, और अभी भी कई प्रश्न हैं जिनका उत्तर दिया जाना आवश्यक है। लेखों की अगली श्रृंखला उत्तर प्रदान करने का प्रयास करेगी।