पिछले लेख में ऑर्डर आगमन अंतराल का अध्ययन किया गया था और प्रदर्शित किया गया था कि हमें मापदंडों को गतिशील रूप से समायोजित करने की आवश्यकता क्यों है और अनुमान की गुणवत्ता का मूल्यांकन कैसे किया जाए। यह लेख गहन आंकड़ों पर ध्यान केंद्रित करेगा और मध्य-मूल्य (जिसे उचित मूल्य, सूक्ष्म मूल्य आदि भी कहा जाता है) का अध्ययन करेगा।

गहराई डेटा

Binance सर्वोत्तम उद्धरणों का ऐतिहासिक डेटा डाउनलोड प्रदान करता है, जिसमें best_bid_price शामिल है: सर्वोत्तम बोली मूल्य, यानी अधिकतम बोली मूल्य, best_bid_qty: सर्वोत्तम बोली मूल्य की संख्या, best_ask_price: सर्वोत्तम पूछ मूल्य, best_ask_qty: सर्वोत्तम पूछ मूल्य की संख्या , transaction_time: टाइमस्टैम्प. इस डेटा में दूसरे स्तर और उससे भी अधिक के लंबित ऑर्डर शामिल नहीं हैं। यहां विश्लेषण की गई बाजार स्थिति 7 अगस्त को YGG है। उस दिन बाजार में उतार-चढ़ाव बहुत अधिक था, और डेटा की मात्रा 9 मिलियन से अधिक तक पहुंच गई थी।

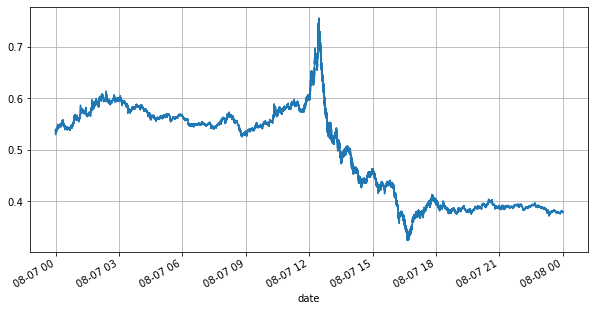
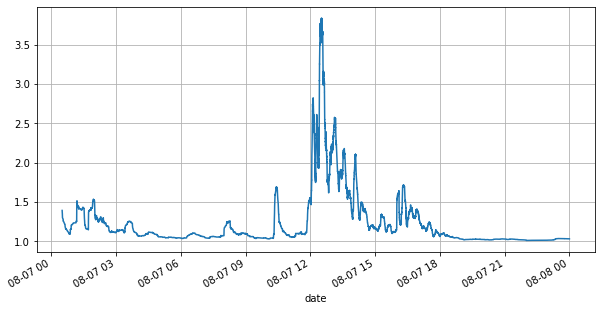
सबसे पहले, दिन के बाजार पर नज़र डालते हैं। इसमें बहुत उतार-चढ़ाव होता है। इसके अलावा, दिन के लंबित ऑर्डर की संख्या भी बाजार के उतार-चढ़ाव के साथ बहुत बदल गई है। विशेष रूप से, स्प्रेड (के बीच का अंतर) विक्रय मूल्य और क्रय मूल्य) ने बाजार में उतार-चढ़ाव की स्थिति को स्पष्ट रूप से दर्शाया है। उस दिन YGG के बाजार के आंकड़ों के अनुसार, 20% समय प्रसार 1 टिक से अधिक था। इस युग में जब विभिन्न रोबोट बाजार पर प्रतिस्पर्धा करते हैं, यह स्थिति दुर्लभ है।

from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

books = pd.read_csv('YGGUSDT-bookTicker-2023-08-07.csv')

tick_size = 0.0001

books['date'] = pd.to_datetime(books['transaction_time'], unit='ms')
books.index = books['date']

books['spread'] = round(books['best_ask_price'] - books['best_bid_price'],4)

books['best_bid_price'][::10].plot(figsize=(10,5),grid=True);

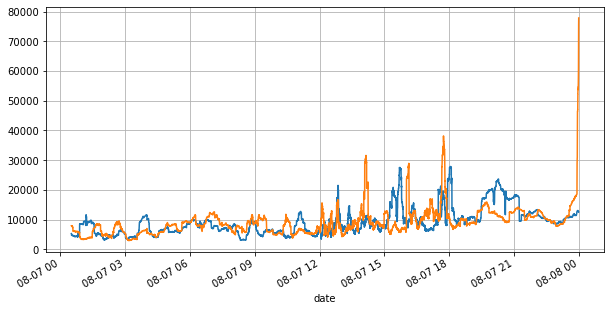
books['best_bid_qty'][::10].rolling(10000).mean().plot(figsize=(10,5),grid=True);
books['best_ask_qty'][::10].rolling(10000).mean().plot(figsize=(10,5),grid=True);

(books['spread'][::10]/tick_size).rolling(10000).mean().plot(figsize=(10,5),grid=True);

books['spread'].value_counts()[books['spread'].value_counts()>500]/books['spread'].value_counts().sum()

0.0001    0.799169
0.0002    0.102750
0.0003    0.042472
0.0004    0.022821
0.0005    0.012792
0.0006    0.007350
0.0007    0.004376
0.0008    0.002712
0.0009    0.001657
0.0010    0.001089
0.0011    0.000740
0.0012    0.000496
0.0013    0.000380
0.0014    0.000258
0.0015    0.000197
0.0016    0.000140
0.0017    0.000112
0.0018    0.000088
0.0019    0.000063
Name: spread, dtype: float64

असंतुलित उद्धरण

उपरोक्त से हम देख सकते हैं कि खरीद और बिक्री के ऑर्डर की मात्रा अधिकांश समय बहुत अलग होती है। इस अंतर का अल्पकालिक बाजार स्थितियों पर एक मजबूत पूर्वानुमानात्मक प्रभाव पड़ता है। इसका कारण पिछले लेख में बताए गए कारण के समान ही है कि छोटे खरीद आदेश अक्सर गिरावट का कारण बनते हैं। यदि एक तरफ लंबित ऑर्डर दूसरी तरफ की तुलना में काफी कम हैं, और यह मानते हुए कि सक्रिय खरीद और बिक्री ऑर्डर की मात्रा करीब है, तो छोटे लंबित ऑर्डर वाले पक्ष के खत्म होने की अधिक संभावना होगी, जिससे कीमत बढ़ जाएगी। परिवर्तन. असंतुलित उद्धरण I द्वारा दर्शाए जाते हैं: 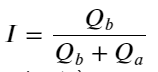जहां Q_b खरीद आदेश मात्रा (best_bid_qty) को दर्शाता है, और Q_a बिक्री आदेश मात्रा (best_ask_qty) को दर्शाता है।

मध्य-मूल्य परिभाषित करें: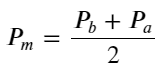

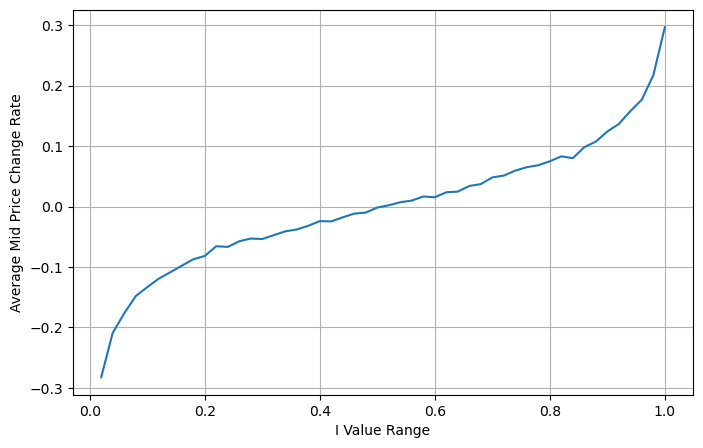
निम्नलिखित आंकड़ा अगले अंतराल में मध्य-मूल्य के परिवर्तन की दर और असंतुलन I के बीच संबंध को दर्शाता है। जैसा कि अपेक्षित था, जैसे-जैसे I बढ़ता है, कीमत बढ़ने की अधिक संभावना होती है और यह 1 के जितना करीब होता है, असंतुलन I का परिमाण उतना ही अधिक होता है। मूल्य परिवर्तन भी तीव्र हो जाता है। हाई-फ़्रीक्वेंसी ट्रेडिंग में, मध्य मूल्य को पेश करने का उद्देश्य भविष्य के मूल्य परिवर्तनों का बेहतर अनुमान लगाना है। दूसरे शब्दों में, भविष्य की कीमत से अंतर जितना छोटा होगा, मध्य मूल्य उतना ही बेहतर परिभाषित होगा। जाहिर है, लंबित ऑर्डर का असंतुलन रणनीति की भविष्यवाणी के लिए अतिरिक्त जानकारी प्रदान करता है। इसे ध्यान में रखते हुए, हम भारित मध्य-मूल्य को परिभाषित करते हैं:

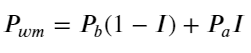
books['I'] = books['best_bid_qty'] / (books['best_bid_qty'] + books['best_ask_qty'])

books['mid_price'] = (books['best_ask_price'] + books['best_bid_price'])/2

bins = np.linspace(0, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['price_change'] = (books['mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['price_change'].mean()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Average Mid Price Change Rate');
plt.grid(True)

books['weighted_mid_price'] = books['mid_price'] + books['spread']*books['I']/2
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['weighted_price_change'] = (books['weighted_mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['weighted_price_change'].mean()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

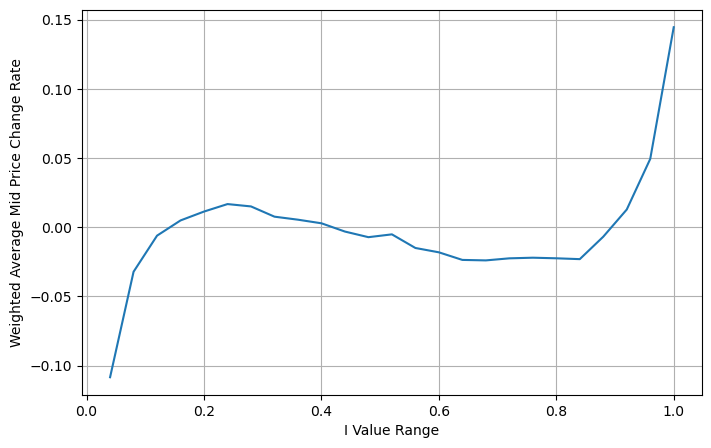
भारित मध्य-मूल्य समायोजित करें

चित्र से हम देख सकते हैं कि भारित मध्य-मूल्य भिन्न I की तुलना में बहुत कम बदलता है, जिसका अर्थ है कि भारित मध्य-मूल्य बेहतर फिट है। लेकिन अभी भी कुछ नियमितताएं हैं, जैसे 0.2 और 0.8 के आसपास, जहां विचलन अपेक्षाकृत बड़े हैं। इससे पता चलता है कि मैं अभी भी अतिरिक्त जानकारी दे सकता हूं। क्योंकि भारित मध्य-मूल्य मानता है कि मूल्य सुधार अवधि I के साथ पूरी तरह से रैखिक है, यह स्पष्ट रूप से सच नहीं है। जैसा कि ऊपर दिए गए चित्र से देखा जा सकता है, जब I 0 और 1 के करीब होता है, तो विचलन तेज़ होता है और यह एक नहीं है रैखिक संबंध.

अधिक सहज ज्ञान के लिए, I को यहां पुनः परिभाषित किया गया है:

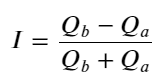
इस समय:

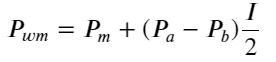
इस रूप को देखते हुए, हम पा सकते हैं कि भारित मध्य-मूल्य औसत मध्य-मूल्य में सुधार है। सुधार अवधि का गुणांक स्प्रेड है, और सुधार अवधि I का एक फ़ंक्शन है। भारित मध्य-मूल्य बस यह मानता है कि यह संबंध I/2 है। इस समय, I (-1,1) के समायोजित वितरण का लाभ परिलक्षित होता है। I मूल के बारे में सममित है, जो फ़ंक्शन के फिटिंग संबंध को खोजने के लिए हमारे लिए सुविधाजनक बनाता है। ग्राफ को ध्यान से देखें, इस फ़ंक्शन को I की विषम शक्ति के संबंध को संतुष्ट करना चाहिए, जो दोनों पक्षों पर तेज़ वृद्धि और मूल के बारे में समरूपता के अनुरूप है। इसके अलावा, यह देखा जा सकता है कि मूल के पास का मान रैखिक के करीब है, और जब I 0 है, तो फ़ंक्शन परिणाम 0 है, और जब I 1 है, तो फ़ंक्शन परिणाम 0.5 है। तो अनुमान लगाइये कि यह फ़ंक्शन कुछ इस प्रकार दिखता है:

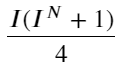
यहाँ N एक धनात्मक सम संख्या है। वास्तविक परीक्षण के बाद, N का मान 8 होना बेहतर है। अब तक, यह आलेख एक संशोधित भारित मध्य मूल्य का प्रस्ताव करता है:

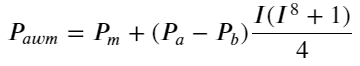
इस बिंदु पर, पूर्वानुमानित मध्य-मूल्य में परिवर्तन का मूलतः I से कोई लेना-देना नहीं है। हालाँकि यह परिणाम सरल भारित मध्य-मूल्य से बेहतर है, लेकिन इसे वास्तविक ट्रेडिंग में लागू नहीं किया जा सकता है। यह यहाँ दिया गया एक विचार मात्र है। एस स्टोइकोव द्वारा 2017 में लिखे गए एक लेख में मार्कोव श्रृंखला विधि प्रस्तुत की गई थीMicro-Price, और प्रासंगिक कोड देता है, आप इसका अध्ययन भी कर सकते हैं।

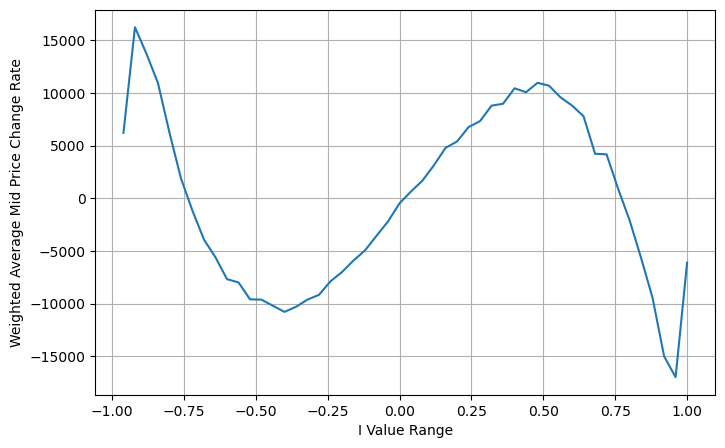
books['I'] = (books['best_bid_qty'] - books['best_ask_qty']) / (books['best_bid_qty'] + books['best_ask_qty'])

books['weighted_mid_price'] = books['mid_price'] + books['spread']*books['I']/2
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['weighted_price_change'] = (books['weighted_mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['weighted_price_change'].sum()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

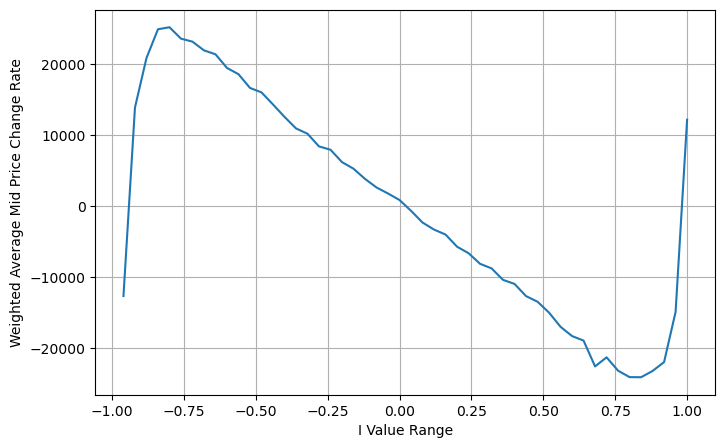
books['adjust_mid_price'] = books['mid_price'] + books['spread']*(books['I'])*(books['I']**8+1)/4
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['adjust_mid_price'] = (books['adjust_mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['adjust_mid_price'].sum()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

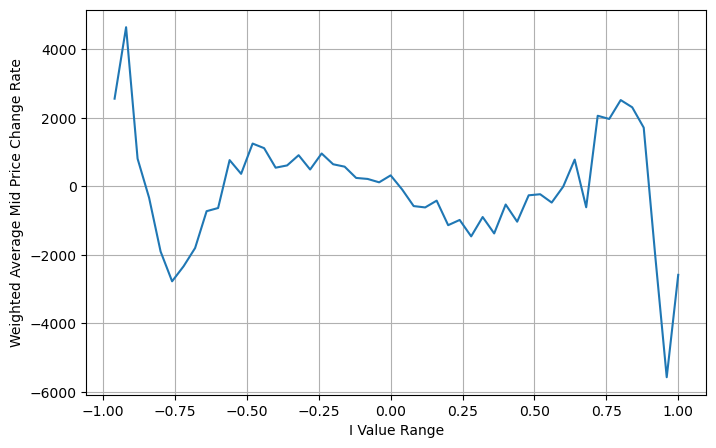
books['adjust_mid_price'] = books['mid_price'] + books['spread']*(books['I']**3)/2
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['adjust_mid_price'] = (books['adjust_mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['adjust_mid_price'].sum()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

संक्षेप

उच्च आवृत्ति रणनीतियों के लिए मध्य मूल्य बहुत महत्वपूर्ण है। यह भविष्य की अल्पकालिक कीमतों का पूर्वानुमान है, इसलिए मध्य मूल्य जितना संभव हो उतना सटीक होना चाहिए। ऊपर प्रस्तुत सभी मध्य मूल्य बाजार के आंकड़ों पर आधारित हैं, क्योंकि विश्लेषण में केवल एक ही बाजार मूल्य का उपयोग किया गया है। वास्तविक व्यापार में, रणनीति को यथासंभव सभी डेटा का उपयोग करना चाहिए, खासकर जब वास्तविक व्यापार में व्यापार एक्सचेंज होते हैं, और मध्य मूल्य की भविष्यवाणी को वास्तविक लेनदेन मूल्य द्वारा परीक्षण किया जाना चाहिए। मुझे याद है कि स्टोइकोव ने एक ट्वीट पोस्ट किया था जिसमें कहा गया था कि वास्तविक मध्य मूल्य एक खरीद-एक-बिक्री लेनदेन की संभावना का भारित औसत होना चाहिए। इस मुद्दे पर पिछले लेख में ही अध्ययन किया गया है। स्थान सीमित होने के कारण, इन मुद्दों पर अगले लेख में विस्तार से चर्चा की जाएगी।