पिछले लेख में विभिन्न मध्य-मूल्यों की गणना विधियों का प्रारंभिक परिचय दिया गया था और मध्य-मूल्य का संशोधन दिया गया था। यह लेख इस विषय पर गहन चर्चा जारी रखता है।

आवश्यक डेटा

ऑर्डर प्रवाह डेटा और गहराई डेटा के दस स्तर वास्तविक ट्रेडिंग से एकत्र किए जाते हैं, और अद्यतन आवृत्ति 100ms है। वास्तविक बाजार में केवल खरीद और बिक्री का डेटा होता है, जिसे वास्तविक समय में अपडेट किया जाता है। सरलता के लिए, इसका उपयोग फिलहाल नहीं किया जाता है। यह देखते हुए कि डेटा बहुत बड़ा है, गहन डेटा की केवल 100,000 पंक्तियाँ ही रखी जाती हैं, और प्रत्येक स्तर के लिए बाजार की स्थितियों को भी अलग-अलग स्तंभों में विभाजित किया जाता है।

from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import ast
%matplotlib inline

tick_size = 0.0001

trades = pd.read_csv('YGGUSDT_aggTrade.csv',names=['type','event_time', 'agg_trade_id','symbol', 'price', 'quantity', 'first_trade_id', 'last_trade_id',
       'transact_time', 'is_buyer_maker'])

trades = trades.groupby(['transact_time','is_buyer_maker']).agg({
    'transact_time':'last',
    'agg_trade_id': 'last',
    'price': 'first',
    'quantity': 'sum',
    'first_trade_id': 'first',
    'last_trade_id': 'last',
    'is_buyer_maker': 'last',
})

trades.index = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index.rename('time', inplace=True)
trades['interval'] = trades['transact_time'] - trades['transact_time'].shift()

depths = pd.read_csv('YGGUSDT_depth.csv',names=['type','event_time', 'transact_time','symbol', 'u1', 'u2', 'u3', 'bids','asks'])

depths = depths.iloc[:100000]

depths['bids'] = depths['bids'].apply(ast.literal_eval).copy()
depths['asks'] = depths['asks'].apply(ast.literal_eval).copy()

def expand_bid(bid_data):
    expanded = {}
    for j, (price, quantity) in enumerate(bid_data):
        expanded[f'bid_{j}_price'] = float(price)
        expanded[f'bid_{j}_quantity'] = float(quantity)
    return pd.Series(expanded)
def expand_ask(ask_data):
    expanded = {}
    for j, (price, quantity) in enumerate(ask_data):
        expanded[f'ask_{j}_price'] = float(price)
        expanded[f'ask_{j}_quantity'] = float(quantity)
    return pd.Series(expanded)
# 应用到每一行，得到新的df
expanded_df_bid = depths['bids'].apply(expand_bid)
expanded_df_ask = depths['asks'].apply(expand_ask)
# 在原有df上进行扩展
depths = pd.concat([depths, expanded_df_bid, expanded_df_ask], axis=1)

depths.index = pd.to_datetime(depths['transact_time'], unit='ms')
depths.index.rename('time', inplace=True);

trades = trades[trades['transact_time'] < depths['transact_time'].iloc[-1]]

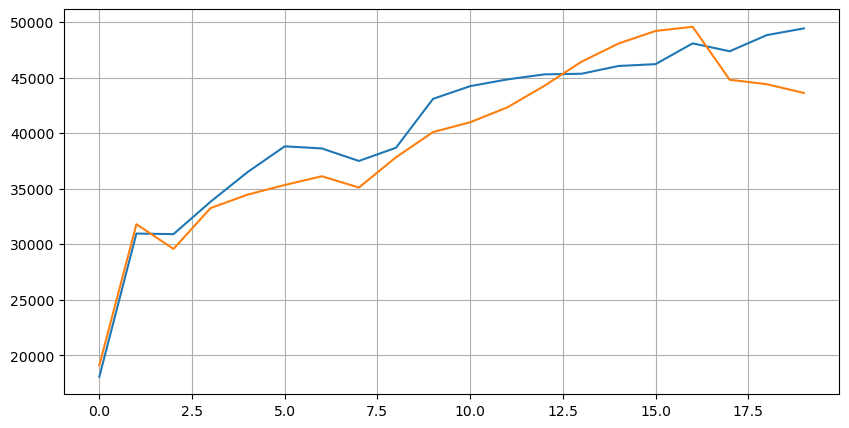
आइए सबसे पहले इन 20 बाजार स्थितियों के वितरण पर नज़र डालें। यह उम्मीदों के अनुरूप है। बाजार खुलने से जितना दूर होगा, उतने ही ज़्यादा लंबित ऑर्डर होंगे, और खरीद ऑर्डर और बिक्री ऑर्डर लगभग सममित होंगे।

bid_mean_list = []
ask_mean_list = []
for i in range(20):
    bid_mean_list.append(round(depths[f'bid_{i}_quantity'].mean(),0))
    ask_mean_list.append(round(depths[f'ask_{i}_quantity'].mean(),0))
plt.figure(figsize=(10, 5))
plt.plot(bid_mean_list);
plt.plot(ask_mean_list);
plt.grid(True)

पूर्वानुमान सटीकता के मूल्यांकन को सुविधाजनक बनाने के लिए गहराई डेटा और लेनदेन डेटा को संयोजित करें। यहाँ हम यह सुनिश्चित करते हैं कि लेन-देन का सारा डेटा गहराई के डेटा से बाद का हो। देरी पर विचार किए बिना, हम सीधे अनुमानित मूल्य और वास्तविक लेन-देन मूल्य के बीच माध्य वर्ग त्रुटि की गणना करते हैं। भविष्यवाणियों की सटीकता मापने के लिए उपयोग किया जाता है।

परिणामों से देखते हुए, खरीद-बिक्री जोड़ी के औसत, mid_price की त्रुटि सबसे बड़ी है। weight_mid_price में बदलने के बाद, त्रुटि तुरंत बहुत छोटी हो जाती है, और भारित मध्य-मूल्य को समायोजित करके इसे और बेहतर बनाया जाता है। कल के लेख के प्रकाशित होने के बाद, कुछ लोगों ने बताया कि उन्होंने केवल I^³⁄₂ का उपयोग किया था। मैंने इसे यहाँ जाँचा और पाया कि परिणाम बेहतर था। कारण के बारे में सोचने के बाद, यह घटनाओं की आवृत्ति में अंतर होना चाहिए। जब ​​I -1 और 1 के करीब होता है, तो यह एक कम संभावना वाली घटना होती है। इन कम संभावनाओं को ठीक करने के लिए, उच्च आवृत्ति वाली घटनाओं की भविष्यवाणी इतना सटीक नहीं है। इसलिए, अधिक उच्च आवृत्ति घटनाओं का ख्याल रखने के लिए, मैंने कुछ समायोजन किए (ये विशुद्ध रूप से प्रायोगिक पैरामीटर हैं, और वास्तविक ट्रेडिंग के लिए बहुत उपयोगी नहीं हैं):

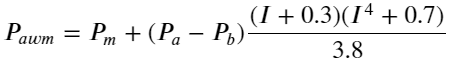
परिणाम थोड़ा बेहतर था. जैसा कि पिछले लेख में बताया गया है, रणनीतियों का पूर्वानुमान अधिक डेटा के साथ लगाया जाना चाहिए। अधिक गहराई और ऑर्डर पूर्ति डेटा के साथ, बाजार मूल्य के साथ उलझाव से जो सुधार प्राप्त किया जा सकता है वह पहले से ही बहुत कमजोर है।

df = pd.merge_asof(trades, depths, on='transact_time', direction='backward')

df['spread'] = round(df['ask_0_price'] - df['bid_0_price'],4)
df['mid_price'] = (df['bid_0_price']+ df['ask_0_price']) / 2
df['I'] = (df['bid_0_quantity'] - df['ask_0_quantity']) / (df['bid_0_quantity'] + df['ask_0_quantity'])
df['weight_mid_price'] = df['mid_price'] + df['spread']*df['I']/2
df['adjust_mid_price'] = df['mid_price'] + df['spread']*(df['I'])*(df['I']**8+1)/4
df['adjust_mid_price_2'] = df['mid_price'] + df['spread']*df['I']*(df['I']**2+1)/4
df['adjust_mid_price_3'] = df['mid_price'] + df['spread']*df['I']**3/2
df['adjust_mid_price_4'] = df['mid_price'] + df['spread']*(df['I']+0.3)*(df['I']**4+0.7)/3.8

print('平均值     mid_price的误差：', ((df['price']-df['mid_price'])**2).sum())
print('挂单量加权 mid_price的误差：', ((df['price']-df['weight_mid_price'])**2).sum())
print('调整后的   mid_price的误差：', ((df['price']-df['adjust_mid_price'])**2).sum())
print('调整后的 mid_price_2的误差：', ((df['price']-df['adjust_mid_price_2'])**2).sum())
print('调整后的 mid_price_3的误差：', ((df['price']-df['adjust_mid_price_3'])**2).sum())
print('调整后的 mid_price_4的误差：', ((df['price']-df['adjust_mid_price_4'])**2).sum())

平均值     mid_price的误差： 0.0048751924999999845
挂单量加权 mid_price的误差： 0.0048373440193987035
调整后的   mid_price的误差： 0.004803654771638586
调整后的 mid_price_2的误差： 0.004808216498329721
调整后的 mid_price_3的误差： 0.004794984755260528
调整后的 mid_price_4的误差： 0.0047909595497071375

दूसरे गियर की गहराई पर विचार करें

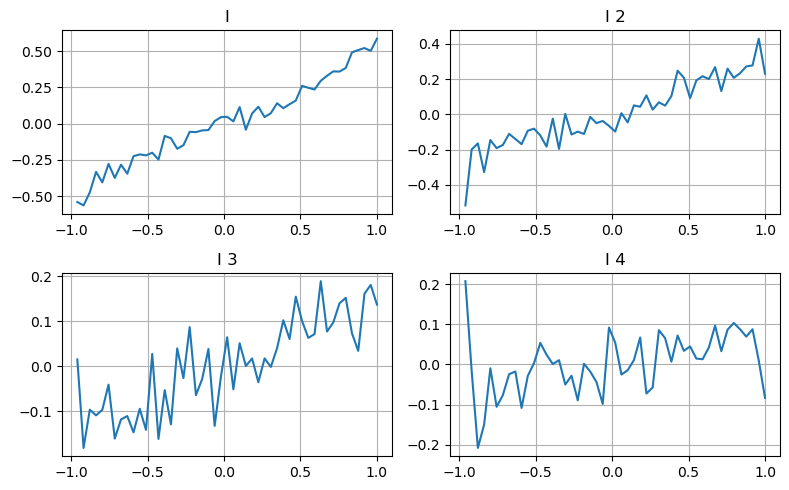
यहां हम पिछले लेख के विचार का उपयोग एक निश्चित प्रभावित करने वाले पैरामीटर के विभिन्न मूल्य श्रेणियों और लेनदेन मूल्य में परिवर्तन की जांच करने के लिए करते हैं ताकि मध्य मूल्य में इस पैरामीटर के योगदान को मापा जा सके। जैसा कि प्रथम-स्तरीय गहराई ग्राफ में दिखाया गया है, जैसे-जैसे I बढ़ता है, अगले लेनदेन मूल्य में सकारात्मक रूप से परिवर्तन होने की अधिक संभावना होती है, जिसका अर्थ है कि I सकारात्मक योगदान देता है।

दूसरे बैच को भी उसी तरीके से संसाधित किया गया, और पाया गया कि यद्यपि प्रभाव पहले बैच की तुलना में थोड़ा कम था, फिर भी यह नगण्य नहीं था। गहराई का तीसरा स्तर भी थोड़ा योगदान देता है, लेकिन एकरसता बहुत खराब है, और अधिक गहराई का मूलतः कोई संदर्भ मूल्य नहीं है।

विभिन्न योगदान स्तरों के अनुसार, तीनों स्तरों के असंतुलन मापदंडों को अलग-अलग भार सौंपा जाता है। वास्तविक निरीक्षण से पता चलता है कि विभिन्न गणना विधियों के लिए पूर्वानुमान त्रुटियाँ और भी कम हो जाती हैं।

bins = np.linspace(-1, 1, 50)
df['change'] = (df['price'].pct_change().shift(-1))/tick_size
df['I_bins'] = pd.cut(df['I'], bins, labels=bins[1:])
df['I_2'] = (df['bid_1_quantity'] - df['ask_1_quantity']) / (df['bid_1_quantity'] + df['ask_1_quantity'])
df['I_2_bins'] = pd.cut(df['I_2'], bins, labels=bins[1:])
df['I_3'] = (df['bid_2_quantity'] - df['ask_2_quantity']) / (df['bid_2_quantity'] + df['ask_2_quantity'])
df['I_3_bins'] = pd.cut(df['I_3'], bins, labels=bins[1:])
df['I_4'] = (df['bid_3_quantity'] - df['ask_3_quantity']) / (df['bid_3_quantity'] + df['ask_3_quantity'])
df['I_4_bins'] = pd.cut(df['I_4'], bins, labels=bins[1:])
fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(8, 5))


axes[0][0].plot(df.groupby('I_bins')['change'].mean())
axes[0][0].set_title('I')
axes[0][0].grid(True)

axes[0][1].plot(df.groupby('I_2_bins')['change'].mean())
axes[0][1].set_title('I 2')
axes[0][1].grid(True)

axes[1][0].plot(df.groupby('I_3_bins')['change'].mean())
axes[1][0].set_title('I 3')
axes[1][0].grid(True)

axes[1][1].plot(df.groupby('I_4_bins')['change'].mean())
axes[1][1].set_title('I 4')
axes[1][1].grid(True)
plt.tight_layout();

df['adjust_mid_price_4'] = df['mid_price'] + df['spread']*(df['I']+0.3)*(df['I']**4+0.7)/3.8
df['adjust_mid_price_5'] = df['mid_price'] + df['spread']*(0.7*df['I']+0.3*df['I_2'])/2
df['adjust_mid_price_6'] = df['mid_price'] + df['spread']*(0.7*df['I']+0.3*df['I_2'])**3/2
df['adjust_mid_price_7'] = df['mid_price'] + df['spread']*(0.7*df['I']+0.3*df['I_2']+0.3)*((0.7*df['I']+0.3*df['I_2'])**4+0.7)/3.8
df['adjust_mid_price_8'] = df['mid_price'] + df['spread']*(0.7*df['I']+0.2*df['I_2']+0.1*df['I_3']+0.3)*((0.7*df['I']+0.3*df['I_2']+0.1*df['I_3'])**4+0.7)/3.8

print('调整后的 mid_price_4的误差：', ((df['price']-df['adjust_mid_price_4'])**2).sum())
print('调整后的 mid_price_5的误差：', ((df['price']-df['adjust_mid_price_5'])**2).sum())
print('调整后的 mid_price_6的误差：', ((df['price']-df['adjust_mid_price_6'])**2).sum())
print('调整后的 mid_price_7的误差：', ((df['price']-df['adjust_mid_price_7'])**2).sum())
print('调整后的 mid_price_8的误差：', ((df['price']-df['adjust_mid_price_8'])**2).sum())

调整后的 mid_price_4的误差： 0.0047909595497071375
调整后的 mid_price_5的误差： 0.0047884350488318714
调整后的 mid_price_6的误差： 0.0047778319053133735
调整后的 mid_price_7的误差： 0.004773578540592192
调整后的 mid_price_8的误差： 0.004771415189297518

लेन-देन डेटा पर विचार करें

लेन-देन डेटा सीधे लंबी और छोटी स्थिति की डिग्री को दर्शाता है। आखिरकार, यह एक ऐसा विकल्प है जिसमें असली पैसे शामिल हैं, और ऑर्डर देने की लागत बहुत कम है, और यहां तक ​​कि जानबूझकर ऑर्डर प्लेसमेंट धोखाधड़ी के मामले भी हैं। इसलिए, मध्य-मूल्य की भविष्यवाणी करते समय, रणनीति को लेनदेन डेटा पर ध्यान केंद्रित करना चाहिए।

फॉर्म पर विचार करते हुए, ऑर्डर औसत आगमन मात्रा असंतुलन को परिभाषित करें VI, Vb, Vs क्रमशः प्रति यूनिट इवेंट खरीद ऑर्डर और बिक्री ऑर्डर की औसत मात्रा का प्रतिनिधित्व करते हैं।

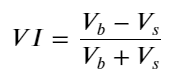
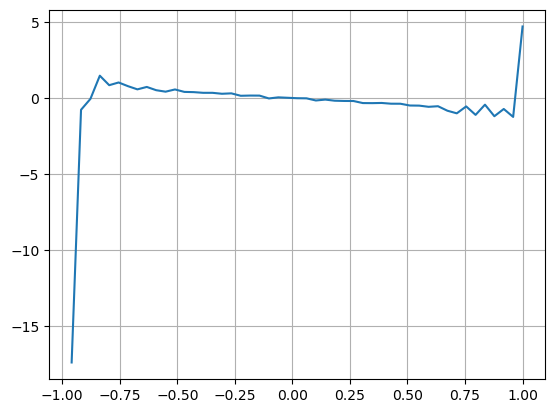
परिणाम दर्शाते हैं कि कम समय में आगमन की मात्रा मूल्य परिवर्तनों की भविष्यवाणी करने में सबसे महत्वपूर्ण है। जब VI (0.1-0.9) के बीच होता है, तो यह मूल्य के साथ नकारात्मक रूप से सहसंबंधित होता है, लेकिन सीमा के बाहर यह मूल्य के साथ सकारात्मक रूप से सहसंबंधित होता है। कीमत। इससे पता चलता है कि जब बाजार चरम पर नहीं होता है, तो यह मुख्य रूप से उतार-चढ़ाव की विशेषता रखता है और कीमतें औसत पर वापस आ जाएंगी। जब चरम बाजार की स्थिति होती है, जैसे कि बड़ी संख्या में खरीद ऑर्डर बिक्री ऑर्डर को भारी कर देते हैं, तो प्रवृत्ति प्रवृत्ति से बाहर निकल जाएगी . भले ही हम इन कम-संभावना वाली स्थितियों को नजरअंदाज कर दें और केवल यह मान लें कि प्रवृत्ति और VI एक नकारात्मक रैखिक संबंध को संतुष्ट करते हैं, मध्य-मूल्य की भविष्यवाणी त्रुटि बहुत कम हो जाती है। सूत्र में a गुणांक को दर्शाता है।

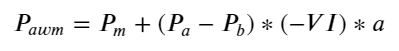
alpha=0.1

df['avg_buy_interval'] = None
df['avg_sell_interval'] = None
df.loc[df['is_buyer_maker'] == True, 'avg_buy_interval'] = df[df['is_buyer_maker'] == True]['transact_time'].diff().ewm(alpha=alpha).mean()
df.loc[df['is_buyer_maker'] == False, 'avg_sell_interval'] = df[df['is_buyer_maker'] == False]['transact_time'].diff().ewm(alpha=alpha).mean()

df['avg_buy_quantity'] = None
df['avg_sell_quantity'] = None
df.loc[df['is_buyer_maker'] == True, 'avg_buy_quantity'] = df[df['is_buyer_maker'] == True]['quantity'].ewm(alpha=alpha).mean()
df.loc[df['is_buyer_maker'] == False, 'avg_sell_quantity'] = df[df['is_buyer_maker'] == False]['quantity'].ewm(alpha=alpha).mean()

df['avg_buy_quantity'] = df['avg_buy_quantity'].fillna(method='ffill')
df['avg_sell_quantity'] = df['avg_sell_quantity'].fillna(method='ffill')
df['avg_buy_interval'] = df['avg_buy_interval'].fillna(method='ffill')
df['avg_sell_interval'] = df['avg_sell_interval'].fillna(method='ffill')

df['avg_buy_rate'] = 1000 / df['avg_buy_interval']
df['avg_sell_rate'] =1000 / df['avg_sell_interval']

df['avg_buy_volume'] = df['avg_buy_rate']*df['avg_buy_quantity']
df['avg_sell_volume'] = df['avg_sell_rate']*df['avg_sell_quantity']

df['I'] = (df['bid_0_quantity']- df['ask_0_quantity']) / (df['bid_0_quantity'] + df['ask_0_quantity'])
df['OI'] = (df['avg_buy_rate']-df['avg_sell_rate']) / (df['avg_buy_rate'] + df['avg_sell_rate'])
df['QI'] = (df['avg_buy_quantity']-df['avg_sell_quantity']) / (df['avg_buy_quantity'] + df['avg_sell_quantity'])
df['VI'] = (df['avg_buy_volume']-df['avg_sell_volume']) / (df['avg_buy_volume'] + df['avg_sell_volume'])

bins = np.linspace(-1, 1, 50)
df['VI_bins'] = pd.cut(df['VI'], bins, labels=bins[1:])
plt.plot(df.groupby('VI_bins')['change'].mean());
plt.grid(True)

df['adjust_mid_price'] = df['mid_price'] + df['spread']*df['I']/2
df['adjust_mid_price_9'] = df['mid_price'] + df['spread']*(-df['OI'])*2
df['adjust_mid_price_10'] = df['mid_price'] + df['spread']*(-df['VI'])*1.4

print('调整后的mid_price   的误差：', ((df['price']-df['adjust_mid_price'])**2).sum())
print('调整后的mid_price_9 的误差：', ((df['price']-df['adjust_mid_price_9'])**2).sum())
print('调整后的mid_price_10的误差：', ((df['price']-df['adjust_mid_price_10'])**2).sum())

调整后的mid_price   的误差： 0.0048373440193987035
调整后的mid_price_9 的误差： 0.004629586542840461
调整后的mid_price_10的误差： 0.004401790287167206

व्यापक औसत मूल्य

यह देखते हुए कि लंबित ऑर्डर और लेनदेन डेटा दोनों ही मध्य मूल्य की भविष्यवाणी करने में सहायक हैं, इन दो मापदंडों को जोड़ा जा सकता है। यहाँ वजन निर्धारण मनमाना है और सीमा स्थितियों पर विचार नहीं करता है। चरम मामलों में, अनुमानित मध्य मूल्य हो सकता है यह नहीं है एक खरीदने और एक बेचने के बीच अंतर हो सकता है, लेकिन जब तक त्रुटि को कम किया जा सकता है, तब तक इन विवरणों का कोई महत्व नहीं है।

अंत में, पूर्वानुमान त्रुटि प्रारंभिक 0.00487 से घटकर 0.0043 हो गई। हम यहाँ विवरण में नहीं जाएँगे। मध्य मूल्य के बारे में अभी भी बहुत कुछ पता लगाना बाकी है। आखिरकार, मध्य मूल्य की भविष्यवाणी करना मूल्य की भविष्यवाणी करना है। आप इसे स्वयं आज़मा सकते हैं .

#注意VI需要延后一个使用
df['price_change'] = np.log(df['price']/df['price'].rolling(40).mean())
df['CI'] = -1.5*df['VI'].shift()+0.7*(0.7*df['I']+0.2*df['I_2']+0.1*df['I_3'])**3 + 150*df['price_change'].shift(1)

df['adjust_mid_price_11'] = df['mid_price'] + df['spread']*(df['CI'])
print('调整后的mid_price_11的误差：', ((df['price']-df['adjust_mid_price_11'])**2).sum())

调整后的mid_price_11的误差： 0.00421125960463469

संक्षेप

यह पेपर मध्य मूल्य की गणना पद्धति को और बेहतर बनाने के लिए गहराई डेटा और लेनदेन डेटा को जोड़ता है। यह पेपर सटीकता को मापने के लिए एक विधि प्रदान करता है और मूल्य परिवर्तनों की भविष्यवाणी करने की सटीकता में सुधार करता है। कुल मिलाकर, विभिन्न पैरामीटर बहुत कठोर नहीं हैं और केवल संदर्भ के लिए हैं। अधिक सटीक मध्य-मूल्य के साथ, अगला चरण वास्तव में बैकटेस्टिंग के लिए मध्य-मूल्य को लागू करना है। इस भाग में भी बहुत सारी सामग्री है, इसलिए हम कुछ समय के लिए अपडेट करना बंद कर देंगे।