Penyortiran FMEX membuka kunci pengoptimalan kuantitas pesanan yang optimal
 0
0
 2308
2308

Runtuhnya FMEX menyebabkan banyak masalah bagi banyak orang, tetapi baru-baru ini muncul rencana memulai kembali dan merumuskan aturan yang mirip dengan penambangan asli untuk melunasi hutang. Artikel analisis telah diberikan tentang penambangan transaksi: https://www.fmz.com/bbs-topic/5834. Ada juga ruang untuk optimasi dalam penambangan penyortiran. Meskipun orang tidak boleh jatuh ke dalam lubang yang sama dua kali, mereka yang memiliki klaim pada FMEX mungkin ingin merujuknya. Strategi real-time spesifik yang dapat dijalankan pada platform kuantitatif FMZ juga dapat dirilis.
Aturan membuka kunci sortir FMEX
Tetapkan setiap 5 menit setiap hari sebagai siklus pembukaan kunci penyortiran, dan setiap siklus dialokasikan 1⁄288 dari kuota pembukaan kunci penyortiran dari pasangan transaksi pada hari itu. Dalam setiap siklus, titik waktu acak dipilih untuk mengambil snapshot dari pesanan beli dan jual dari pasangan perdagangan, di mana:
- Beli 1 Berdasarkan proporsi jumlah pesanan pengguna, 1⁄4 dari jumlah pengembalian periode pembukaan kunci dialokasikan ke peringkat ini
- Jual 1 Menurut proporsi jumlah pesanan pengguna, 1⁄4 dari jumlah pengembalian periode pembukaan kunci dialokasikan ke peringkat ini
- Untuk 4 tingkatan beli 2 untuk beli 5, 1⁄40 dari jumlah pengembalian periode pembukaan akan dialokasikan ke setiap tingkatan sesuai dengan proporsi jumlah pesanan pengguna di setiap tingkatan.
- Untuk pesanan dalam 4 level jual 2 hingga jual 5, 1⁄40 dari jumlah pengembalian periode pembukaan peringkat akan dialokasikan sesuai dengan proporsi jumlah pesanan pengguna di setiap level.
- Untuk lima pesanan dari Beli 6 hingga Beli 10, 1⁄50 dari jumlah pengembalian periode pembukaan kunci akan dialokasikan ke setiap pesanan sesuai dengan proporsi jumlah pesanan di setiap pesanan.
- Untuk lima tingkatan pesanan jual dari 6 hingga 10, 1⁄50 dari jumlah pengembalian periode pembukaan akan dialokasikan ke setiap tingkatan sesuai dengan proporsi jumlah pesanan pengguna di setiap tingkatan.
- Untuk lima pesanan dari Beli 11 hingga Beli 15, 1⁄100 dari jumlah pengembalian periode pembukaan kunci akan dialokasikan ke setiap pesanan sesuai dengan proporsi jumlah pesanan di setiap pesanan.
- Untuk lima pesanan dari Jual 11 hingga Jual 15, 1⁄100 dari jumlah pengembalian periode pembukaan kunci akan dialokasikan ke setiap pesanan sesuai dengan proporsi jumlah pesanan di setiap pesanan.
Total pengembalian dari pembukaan peringkat pengguna dalam pasangan perdagangan tertentu di hari yang sama adalah jumlah uang yang dikembalikan pada pengguna untuk pembukaan peringkat di setiap siklus pasangan perdagangan.
Menyortir untuk membuka manfaat
Pertama, total pendapatan dari sortir dan unlock adalah:
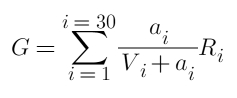
Di sini, i melambangkan salah satu posisi, terdapat 30 posisi secara total untuk kedua belah pihak, a merupakan jumlah pesanan yang tertunda, R merupakan jumlah pengembalian yang dibuka, dan V merupakan jumlah total pesanan yang ada.
Tidak seperti membuka transaksi, pemesanan tidak dikenakan biaya. Di sini, R hanya perlu mempertimbangkan ukuran relatif, dan tidak perlu mempertimbangkan jumlah absolut yang didenominasi dalam USDT. Jika kita menentukan jumlah total order yang tertunda, pertanyaannya adalah bagaimana mengalokasikan order ke posisi yang berbeda untuk memaksimalkan keuntungan G. Sekadar mencari lokasi dengan jumlah pesanan terkecil dan menempatkan semua pesanan di sana jelas bukan solusi optimal. Misalnya, ada tiga posisi dengan 10 order yang ada, dan R mereka sama. Kami menetapkan total volume order menjadi 30. Jika kami hanya memilih satu posisi untuk menempatkan order, total keuntungan akhir adalah 0,75R. 10, keuntungan akhir adalah 1,5R, yang menunjukkan bahwa terkadang keuntungan dari pesanan yang tersebar lebih baik. Jadi bagaimana Anda mengalokasikan dana?
Optimalisasi membuka kunci penyortiran
Terakhir, tujuan dan kendala optimasi kami adalah:
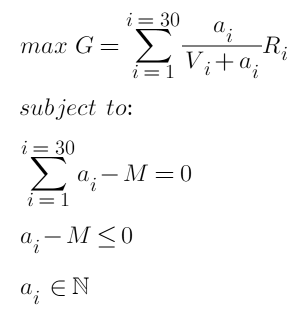
Di mana M adalah jumlah total pesanan. Ini adalah masalah optimasi cembung kuadrat yang melibatkan pertidaksamaan, yang memenuhi kondisi KTT dan memiliki solusi integer. Dengan menggunakan paket yang sesuai dan penyelesai optimasi cembung, seharusnya memungkinkan untuk langsung memperoleh hasil dan mengembalikan kuantitas pesanan optimal untuk setiap posisi. Namun, ini jelas bukan jawaban yang kita inginkan. Kita perlu menyederhanakan masalah dan mendapatkan langkah-langkah solusi yang spesifik.
Mari kita mulai dengan contoh sederhana
Pertimbangkan hanya dua tingkatan. Volume pesanan saat ini adalah 10 dan 20 (masing-masing disebut sebagai tingkatan pertama dan tingkatan kedua). Kuota pembukaannya adalah R. Jumlah total pesanan cadangan strategi adalah 30. Bagaimana cara mengalokasikannya? Apakah jumlah dana yang dibuka telah dimaksimalkan? Pertanyaan ini tampaknya sederhana, tetapi sulit untuk menarik kesimpulan yang tepat tanpa perhitungan. Pembaca mungkin ingin memikirkan jawabannya sendiri terlebih dahulu.
Skenario 1:
Temukan posisi pesanan minimum dan tempatkan semua pesanan di sana, total keuntungan G=30/(30+10)=0,75R. Ini juga merupakan solusi termudah untuk dipikirkan.
Skenario 2:
1 yuan dialokasikan setiap waktu dan dialokasikan ke tempat yang dapat menghasilkan keuntungan terbesar, yaitu tempat dengan jumlah pesanan tertunda terkecil. Kemudian yuan pertama akan dialokasikan ke tingkat pertama, dan volume pesanan tingkat pertama akan menjadi 10+1. Yuan kedua juga akan dialokasikan ke tingkat pertama… dan seterusnya, hingga totalnya menjadi 10 yuan dialokasikan ke tingkat pertama. Pada saat ini, Satu akan dipilih secara acak, dan ketika jumlah total pesanan yang tertunda di tingkat pertama melebihi 20, maka akan dialokasikan ke tingkat kedua. Hasil akhirnya adalah 20 yuan dialokasikan ke tingkat pertama dan 10 yuan dialokasikan ke tingkat kedua, dan pesanan akhir mereka berdua adalah 30. Keuntungan total G=20⁄30+10⁄30=R. Solusi ini jauh lebih baik daripada Solusi 1 dan juga lebih mudah dihitung.
Skenario 3:
Kita dapat mengasumsikan bahwa tingkat pertama dialokasikan a, dan tingkat kedua adalah 30-a. Kemudian kita dapat langsung mencantumkan persamaan dan menemukan turunannya sebagai 0 (prosesnya tidak tercantum di sini, ini mirip dengan artikel tentang membuka kunci transaksi) ), dan hitung hasil akhirnya. Rumusnya adalah:
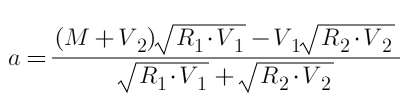
Substitusikan ke bilangan bulat dan dapatkan a=15. Total keuntungan G=15⁄25+15⁄35=1,0286R, yang lebih baik daripada Opsi 2. Karena langsung berasal dari rumus, ini adalah solusi optimal. Pembaca dapat memeriksanya.
Hasilnya mungkin berbeda dari yang Anda harapkan. Jelas bahwa alokasi setiap dolar dalam Rencana 2 adalah solusi optimal dalam situasi saat ini. Mengapa itu bukan solusi optimal secara keseluruhan? Situasi ini sangat umum. Optimum lokal belum tentu merupakan optimum keseluruhan, karena sebelum alokasi, pesanan sudah memiliki dana investasi, dan efisiensi keseluruhan perlu mempertimbangkan biaya hangus. Sasaran kami untuk setiap langkah pengoptimalan adalah memaksimalkan efisiensi keseluruhan daripada memaksimalkan satu manfaat saja.
Rencana optimasi khusus
Akhirnya, kita telah memulai operasi yang sebenarnya. Mari kita sederhanakan masalah dengan mengalokasikan 1 yuan setiap kali. Pertama, mari kita ukur efisiensinya. Turunannya dapat mencerminkan kontribusi masing-masing a terhadap G. Kontribusi ini memperhitungkan biaya kumulatif, bukan manfaat dari satu distribusi. Semakin besar nilainya, semakin besar kontribusi keseluruhan terhadap manfaat akhir. Jelasnya, menurut grafik fungsi, ketika a=1, efisiensi adalah yang tertinggi dari ada hingga tidak ada, dan kemudian secara bertahap menurun.
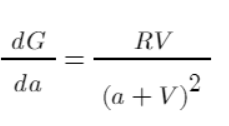
Mengambil contoh sederhana di atas sebagai contoh, kita dapat menghitung efisiensi alokasi dana mereka dan mencantumkannya dalam sebuah tabel:
| dana | 1 | 2 |
|---|---|---|
| 1 | 0.0826 | 0.0454 |
| 2 | 0.069 | 0.0413 |
| 3 | 0.0592 | 0.0378 |
| 4 | 0.051 | 0.0347 |
| 5 | 0.0444 | 0.032 |
| … | … | … |
|12 | 0.0207 |0.0195| |13 | 0.0189 |0.0184| |14 | 0.0174 |0.0173| |15 | 0.016 |0.0163| |16 | 0.0148 |0.0154| |17 | 0.0137 |0.0146| |18 | 0.0128 |0.0139|
Berdasarkan tabel, yuan pertama dialokasikan ke tingkat pertama, yuan kedua dialokasikan ke tingkat pertama… yuan kelima dialokasikan ke tingkat kedua… dan seterusnya, dan akhirnya 15 yuan dialokasikan ke tingkat pertama dan 15 yuan ke tingkat kedua. Yuan, yang merupakan solusi optimal yang kami hitung berdasarkan persamaan. Khusus untuk gigi ke-30, algoritmanya sama, dan langkah-langkah spesifiknya adalah:
- 1. Periksa semua roda gigi terlebih dahulu. Jika V=0, maka a=1, dan tidak akan ada lagi dana yang dialokasikan.
- 2. Alokasikan total dana ke dalam N bagian, dan pilih satu perlengkapan untuk dialokasikan setiap waktu.
- 3. Hitunglah efisiensi masing-masing roda gigi = RV/pow(a+V,2), di mana a merupakan akumulasi dana yang dialokasikan pada posisi + dana yang dialokasikan saat ini.
- 4. Alokasikan dana pada peralatan yang paling efisien, dan pilih secara acak satu jika efisiensinya sama.
- 5. Ulangi 3-4 sampai dana dialokasikan
Jika total volume pesanan kita besar, akan terlalu tidak efisien untuk mengalokasikan setiap dolar pada satu waktu. Kita dapat membagi dana menjadi 100 bagian dan mengalokasikan satu bagian pada satu waktu. Karena ini hanya perhitungan dan penyortiran sederhana, algoritmanya sangat efisien. Khususnya pada tingkat eksekusi, masih ada ruang untuk pengoptimalan, seperti membagi pesanan menjadi 100, sehingga setiap kali kami membuat penyesuaian, kami hanya perlu mengalokasikan kembali pesanan tersebut dan tidak perlu membatalkan semuanya. Anda juga dapat menetapkan sendiri nilai R dan memberi bobot lebih kepada mereka yang jauh dari pasar. Jika ada tumpang tindih antara sort unlocking dan pending order unlocking, Anda dapat mempertimbangkannya bersama-sama, dan seterusnya.
Artikel ini merupakan artikel asli dari FMZ Quantitative Platform. Harap cantumkan sumbernya saat mentransfer: https://www.fmz.com/bbs-topic-new/5843