アルファ・ドッグの利口: モンテカルロのアルゴリズム,読み終えたらわかる!

今年3月9日から15日まで,韓国ソウルで5回の人間対機械の大戦が開催されました. この試合の結果,人類は敗退し,世界ゴーシュ選手権のリー・シシは,グーグル社の人工知能プログラムAlphaGoに1対4で敗れた. ではAlphaGoとは何か? 勝利の秘訣はどこにあるのか? ここで,モンテカルロアルゴリズムについて説明します.

• ### AlphaGoとモンテカルロのアルゴリズム

新華社によると,AlphaGoは,Google社のDeepMindチームによって開発された,中国人ゲームファンから”アルファ・クソ” (アルファ・クソ) と呼ばれている,人対機械のゲームである.

前回の記事では,Googleが開発している神経ネットワークアルゴリズムについて書きました. AlphaGoは,機械学習を自動化するために開発されているものです.

中国自動化協会の副会長兼事務局長王飛跃は,プログラマはゴーホールを熟知する必要はないが,基本ルールを知っているだけでよいと述べた.AlphaGoの背後にいるのは,優れたコンピュータ科学者であり,正確には,機械学習分野の専門家である.科学者は,神経ネットワークアルゴリズムを使用して,チェス専門家の試合記録をコンピュータに入力し,コンピュータが自分自身と試合をさせ,この過程で常に学習訓練を行う.ある意味では,AlphaGoのチェス技は開発者が教えることではなく,自己学習の成才であると言えます.

モンテカルロのアルゴリズムです. モンテカルロのアルゴリズムとは, モンテカルロのアルゴリズムとは, モンテカルロのアルゴリズムとは, モンテカルロのアルゴリズムとは, モンテカルロのアルゴリズムとは, モンテカルロのアルゴリズムとは, モンテカルロのアルゴリズムとは

モンテカルロアルゴリズムとは何か? モンテカルロアルゴリズムの説明はこうです もし,バスケットに1000個のリンゴがあって,あなたが目を閉じて最大を選ばせるなら,選択の回数に制限はありません. 目を閉じてランダムに1つを選び,次にランダムに1つを選び,最初の1つと比較して,大きな1つを残し,次にランダムに1つを選び,前回の1つと比較して,大きな1つを残すことができます.

つまり,モンテカルロアルゴリズムは,サンプル数が多くなるほど,最適の解を見つけることができます.しかし,それが最善であるとは保証されません. 10,000個のリンゴがあれば,より大きなものを見つけることが可能だからです.

ラスベガスのアルゴリズムと比べると, 俗説では,もし,一つの錠前があり,1000個の鍵が選択されているが,正しいのは1つしかいないとする.したがって,ランダムに1つの鍵を取り出して,開けなかったときは1つずつ交換する.試す回数が多いほど,最良の解を開けるチャンスはより大きくなるが,開く前に,間違った鍵は役に立たない.

だからラスベガスのアルゴリズムは,可能な限り最良の解決法であるが,必ずしも見つけられない. 千の鍵のうち,開ける鍵が1つも存在しないと仮定し,本当の鍵は1001番目の鍵であるが,サンプルには1001番目のアルゴリズムがないので,ラスベガスのアルゴリズムは,開ける鍵を見つけられない.

AlphaGoのモンテカルロアルゴリズム Goは人工知能にとって非常に難しいゲームです. Goの落とし方が多すぎて,コンピュータが識別するのが難しいからです. 王飛躍曰く: 第一に,ゴーチェーの可能性はあまりにも多い。ゴーチェーの各ステップの可能な下法は非常に多い,チェア選手が始めるときには19×19=361種類の落下選択がある。一局150ラウンドのゴーチェーの可能性は10170種類まである。第二に,規則はあまりにも微妙で,ある程度落下選択は経験の蓄積によって形成された直感に依存している。さらに,ゴーチェーの棋局において,コンピュータは,現在の棋局の優点と弱点を区別するのが難しい。したがって,ゴーチェーの挑戦は人工知能のアポロ計画と呼ばれる。

AlphaGoはモンテカルロアルゴリズムだけでなく,モンテカルロアルゴリズムのアップグレード版でもある.

AlphaGoは,モンテカルロのツリー検索アルゴリズムと2つの深層神経ネットワークの協力により,チェスを完成させた.李世石との対決の前に,Googleは,まず,人間の対のほぼ3千万の歩き方を用いて,アルファ・ドッグの神経ネットワークを訓練し,それが人間のプロチェス選手がどのように落ちるか予測することを学ぶようにした.さらに,AlphaGo自身にチェスをさせ,それにより,大規模な全新チェスプロットが生成された.Googleのエンジニアは,AlphaGoは,毎日百万の歩き方を試みることができると宣言した.

協働して,より有望なチェスステップを選出し,明らかに欠けているチェスを捨てて,計算をコンピュータが実行できる範囲に制限する.これは本質的に,人間のチェス選手がやっていることと同じだ.

中国科学院自動化研究所の研究者易建強は,の伝統的なチェスソフトは,一般的に暴力的な検索を採用し,深青コンピュータを含む,それはすべての可能な結果に対して検索ツリーを建設し (それぞれの結果は木の1つの果実である),必要に応じて横断検索を行う.この方法は,チェス,ジャンプチェスなどにおいてある程度実現可能である.しかし,ゴーグルでは,ゴーグルが各19行横断し,落とし穴の可能性が大きすぎて,コンピュータがこの木を構成できない (果実が多すぎる) のため,横断検索を行うことは不可能である.AlphaGoは,非常に賢い方法を採用し,この問題を解決した.それは,ディープ・ラーニングの方法を利用して,検索の複雑性を低下させ,検索スペースを効率的に削減した.例えば,戦略的なネットワークは,人間の落とし穴の位置を高く評価するように検索するコンピュータを指揮し,ネットワークは,落とし穴の位置を勝ち取った後にコンピュータが勝利する可能性が高いことを指揮する.

ガチはさらに,深層神経ネットワークの最も基本的な単体は,私たちの人間の脳のニューロンのようなもので,多くの層が接続され,人間の脳のニューロンのネットワークであるかのように説明しました.AlphaGoの2つのニューロンのネットワークは,戦略ネットワークと評価ネットワークです.

の戦略ネットワークは,主に落下戦略を生成するために使用される.チェックの過程で,それは自分がどう下すべきかを考えるのではなく,人間の上手はどう下るべきかを考える.つまり,それは,入力チェスの現在の状態に基づいて,人間の次のチェスがどこに下るのかを予測し,人間の思考に最も適合するいくつかの実行可能な下法を提唱する.

しかし,策略ネットワークは,それがうまくいくかどうかを知らず,それが人間と同じかどうかしか知らないので,評価ネットワークが機能します.

ガチはこう言った:値ネットワークは,可能な各下法のために全体の盤面の状況を評価し,その後勝利率を与える.これらの値は,モンテカルロツリー検索アルゴリズムに反射され,上記のプロセスを繰り返して勝利率の最高を演出する.モンテカルロツリー検索アルゴリズムは,戦略ネットワークが勝利率の高い場所でのみ継続することを決定し,このようにして,特定の路線を放棄し,黒にたどり着くための道を作らない.

AlphaGoは,この2つのツールを活用して,状況の分析を行い,各下子戦略の優劣を判断する.これは,人間のチェス選手が現在の状況を判断し,将来の状況を推論するのと同じです.例えば,次の20ステップの場合,モンテカルロツリー検索アルゴリズムを利用して分析することで,下子で勝つ確率が高い場所が判断できるのです.

モンテカルロのアルゴリズムは,AlphaGoの核心の一つであることは間違いありません.

2つの小さな実験 最後に,モンテカルロアルゴリズムの2つの小さな実験を見てみましょう.

• ### 1. 円周率を計算する

原則:まず,正方形を描き,その内切りの円を描き,次に,この正方形内のランダムな描画点を,円内の点を概してPとして設定し,P=円面積/正方形面積である. P=(Pi*R*R)/(2R*2R) = Pi/4 つまり Pi=4P

ステップ: 1. 円の中心を原点に置き,半径をRで円を作ると,第1四方の円の面積はPi*R*R/4 2. この1/4円の外接正方形を, 座標は, R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R,R*R 3. 任意の点 (x,y) を選んで,0<=X<=Rと0<=Y<=R,つまり点が正方形内にあるようにします. 4. 式Xから*X+Y*Y*R判定点は1/4円圏内にあるかどうか. 5. すべての点 (すなわち実験回数) を N とし,四分の一の円内の点 (すなわちステップ4を満たす点) を M とすると,

これは,P=M/Nです. Pi=4です.*N/M 写真1

M_C ((10000) の実行結果は 3.1424 です.

• ### 2. 局所的極限に陥らないように,モンテカルロは模擬求関数の極限値を求めます.

♪ その間[-2,2] をランダムに生成し,y を求め,最大値の関数である[絶対値の -2,2 よりも大きい値 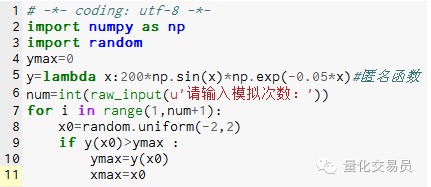画像2

1000回シミュレーションした結果,最大値が185.12292832389875であることが判明しました.

プログラミングは手書きでできるので面白いですね! 微信公論号より転送