高頻度取引戦略についての考察(1)
 3
3
 4856
4856

この記事では、デジタル通貨の高頻度取引戦略について、利益源(主に市場変動と取引所手数料のリベート)、発注とポジション管理の問題、パレート分布を使用した取引量のモデル化方法などについて説明します。さらに、バックテストにはBinanceが提供する取引データと最適注文データが使用され、高頻度取引戦略のその他の問題については、今後の記事で詳しく説明する予定です。
私は以前、デジタル通貨の高頻度取引についての記事を 2 つ書きました。 デジタル通貨の高頻度戦略の詳細な紹介, 5日間で80倍稼ぐ、高頻度戦略の威力。しかし、それは経験の共有と一般的な話としてしか考えられません。今回は、高頻度取引の考え方を最初から紹介する一連の記事を書く予定です。できるだけ簡潔で明確にしたいと考えています。しかし、高頻度取引に関する私のレベルと深い理解が限られているため、取引に関しては、この記事は単なる出発点にすぎません。専門家が私を訂正してくれることを願っています。
高頻度の利益源
以前の記事で述べたように、高頻度戦略は、変動が極めて激しい市場に特に適しています。全体的な傾向と変動で構成される、短期間での取引商品の価格変動を調べます。トレンドの変化を正確に予測できれば、確かに利益を上げることはできますが、これが最も難しいことでもあります。この記事では主に高頻度メイカー戦略を紹介し、この問題には触れません。変動の激しい市場では、上下に注文を出す戦略が十分に頻繁に実行され、利益率が十分に大きければ、トレンドによって生じる可能性のある損失をカバーできるため、市場を予測しなくても利益を上げることができます。現在、取引所でのすべてのメイカー取引は、取引手数料のリベートを受けており、これも利益の構成要素です。競争が激しくなればなるほど、リベートの割合は高くなるはずです。
解決すべき問題
この戦略では、買い注文と売り注文を同時に出します。最初の質問は、どこに注文を出すかということです。注文が市場に近いほど、取引の確率が高くなります。しかし、変動の激しい市場では、瞬間的な取引価格が市場から遠く離れている可能性があります。注文が近すぎると、十分な利益を得る。遠すぎる注文が実行される可能性は低くなります。これは最適化する必要がある問題です。
自分の位置をコントロールする。リスクを制御するために、この戦略では長期間にわたってあまり多くのポジションを蓄積することはできません。これは、注文距離、注文数量、合計ポジション制限などを制御することで解決できます。
上記の目標を達成するためには、取引確率、取引利益、市場予測などをモデル化して推定する必要があります。この分野には多くの記事や論文があり、高頻度取引などのキーワードで見つけることができます。 、オーダーブックなどネット上にはたくさんの推奨事項がありますが、ここでは詳しく説明しません。さらに、信頼性が高く高速なバックテスト システムを確立することが最善です。高頻度戦略は実際の取引を通じて簡単に検証してその有効性を検証できますが、バックテストを行うことでさらに多くのアイデアが得られ、試行錯誤のコストを削減できます。
必要なデータ
Binanceは取引ごとのデータとベストオーダーデータを提供するダウンロードディープデータは、ホワイトリスト内の API を使用してダウンロードするか、自分で収集する必要があります。バックテストの目的では、収集された取引データを使用できます。この記事では、HOOKUSDT-aggTrades-2023-01-27 のデータを例に挙げます。
from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
トランザクション列は次のとおりです。
- agg_trade_id: 集約された取引注文のID、
- 価格: 取引価格
- 数量: 取引数
- first_trade_id: コレクションには同時に複数のトランザクションが存在する場合がありますが、カウントされるのは 1 つのデータのみです。これは最初のトランザクションの ID です。
- last_trade_id: 最後の取引のID
- transact_time: トランザクション時間
- is_buyer_maker: 取引の方向。True は、買い注文がメーカーによって取引され、売り注文がテイカーによって取引されることを意味します。
当日は66万件の取引データがあり、取引が非常に活発だったことがわかります。 CSV はコメントセクションに添付されます。
trades = pd.read_csv('COMPUSDT-aggTrades-2023-07-02.csv')
trades
664475 rows × 7 columns
| agg_trade_id | price | quantity | first_trade_id | last_trade_id | transact_time | is_buyer_maker |
|---|---|---|---|---|---|---|
| 120719552 | 52.42 | 22.087 | 207862988 | 207862990 | 1688256004603 | False |
| 120719553 | 52.41 | 29.314 | 207862991 | 207863002 | 1688256004623 | True |
| 120719554 | 52.42 | 0.945 | 207863003 | 207863003 | 1688256004678 | False |
| 120719555 | 52.41 | 13.534 | 207863004 | 207863006 | 1688256004680 | True |
| … | … | … | … | … | … | … |
| 121384024 | 68.29 | 10.065 | 210364899 | 210364905 | 1688342399863 | False |
| 121384025 | 68.30 | 7.078 | 210364906 | 210364908 | 1688342399948 | False |
| 121384026 | 68.29 | 7.622 | 210364909 | 210364911 | 1688342399979 | True |
単一トランザクションボリュームモデリング
まず、データを処理し、元の取引を買い注文のアクティブな取引グループと売り注文のアクティブな取引グループに分割します。また、元の集計取引データは、同じ時間、同じ価格、同じ方向のデータです。100のアクティブな買い注文があるかもしれません。それが異なる価格の複数の取引に分割されている場合、 60 と 40 のように 2 つのデータが生成され、購入注文量の推定に影響します。そのため、transact_time に基づいて再度集計する必要があります。集約後、データ量は 140,000 件削減されました。
trades['date'] = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index = trades['date']
buy_trades = trades[trades['is_buyer_maker']==False].copy()
sell_trades = trades[trades['is_buyer_maker']==True].copy()
buy_trades = buy_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
sell_trades = sell_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
buy_trades['interval']=buy_trades['transact_time'] - buy_trades['transact_time'].shift()
sell_trades['interval']=sell_trades['transact_time'] - sell_trades['transact_time'].shift()
print(trades.shape[0] - (buy_trades.shape[0]+sell_trades.shape[0]))
146181
買い注文を例にとると、まずヒストグラムを描きます。ロングテール効果が非常に顕著であることがわかります。データのほとんどは左端に集中していますが、少数の大きな取引も裾に分散しています。 。
buy_trades['quantity'].plot.hist(bins=200,figsize=(10, 5));
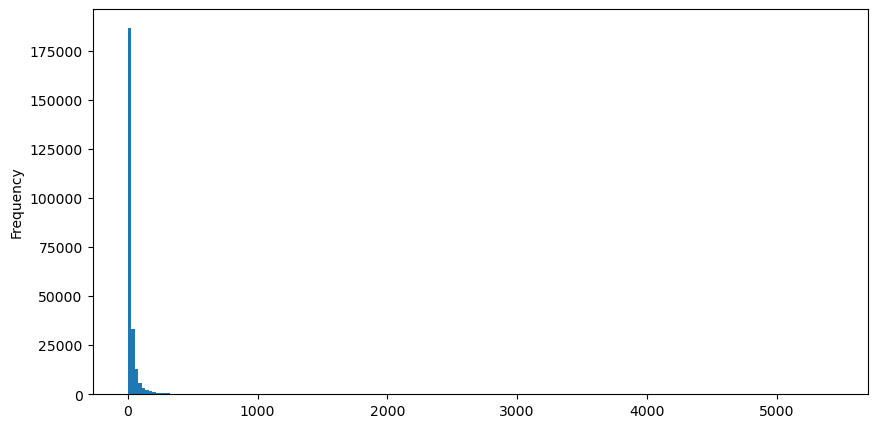
観察の便宜上、裾を切り取って観察します。取引量が大きいほど、発生頻度が低くなり、減少の傾向が速くなることがわかります。
buy_trades['quantity'][buy_trades['quantity']<200].plot.hist(bins=200,figsize=(10, 5));
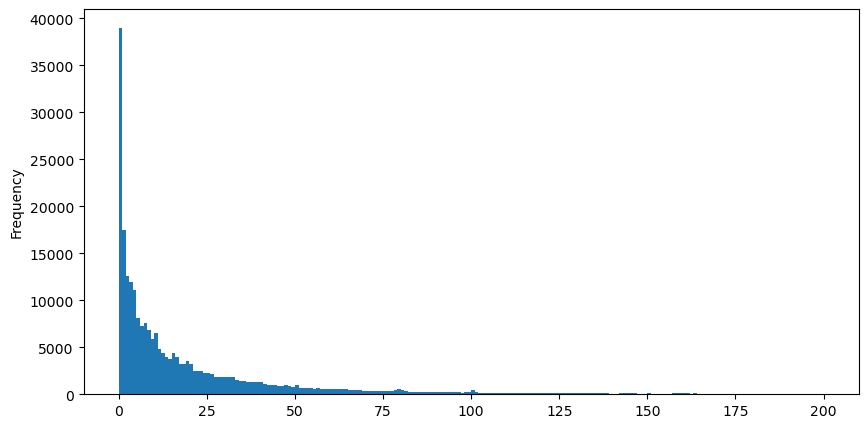
ボリューム満足度の分布に関する研究は数多くあります。そのべき乗分布はパレート分布とも呼ばれ、統計物理学や社会科学における確率分布の一般的な形式です。べき乗分布では、特定のサイズ (または頻度) のイベントの確率は、そのイベントのサイズの負の指数に比例します。この分布形式の主な特徴は、大きなイベント (つまり、平均から遠いイベント) が、他の多くの分布で予想されるよりも頻繁に発生することです。これが取引量分布の特徴です。パレート分布の形式は、P(x) = Cx^(-α) です。以下でこれを説明します。
下の図は、取引量が特定の値を超える確率を示しています。青い線は実際の確率で、オレンジ色の線はシミュレートされた確率です。ここでは特定のパラメータについては心配する必要はありません。パレート分布を満たす。注文量が 0 より大きい確率は 1 であり、標準化の要件を満たすためには、分布方程式は次のようになります。
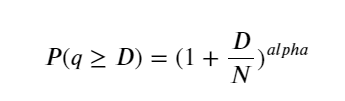
ここで、N は標準化されたパラメータです。ここでは、平均ボリューム M とアルファ -2.06 を選択します。アルファの特定の推定値は、D = N の場合の P 値を逆に計算することによって計算できます。具体的には、alpha = log(P(d>M))/log(2)です。異なるポイントを選択すると、アルファ値がわずかに異なります。
depths = range(0, 250, 2)
probabilities = np.array([np.mean(buy_trades['quantity'] > depth) for depth in depths])
alpha = np.log(np.mean(buy_trades['quantity'] > mean_quantity))/np.log(2)
mean_quantity = buy_trades['quantity'].mean()
probabilities_s = np.array([(1+depth/mean_quantity)**alpha for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)
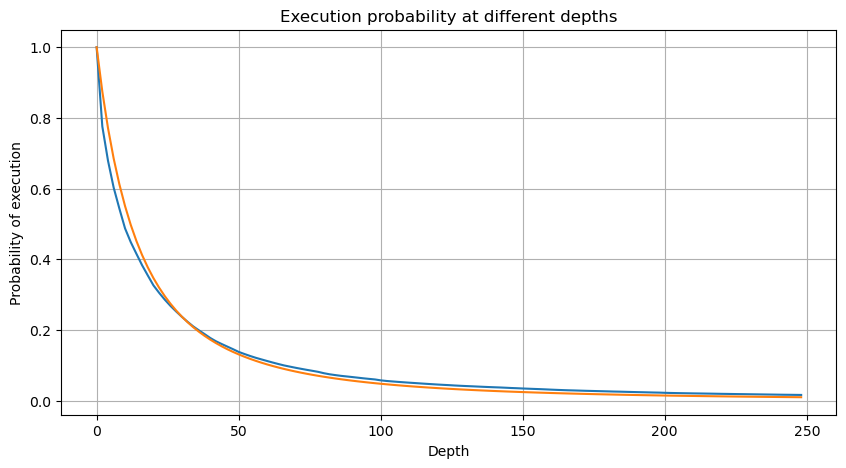
plt.figure(figsize=(10, 5))
plt.grid(True)
plt.title('Diff')
plt.plot(depths, probabilities_s-probabilities);
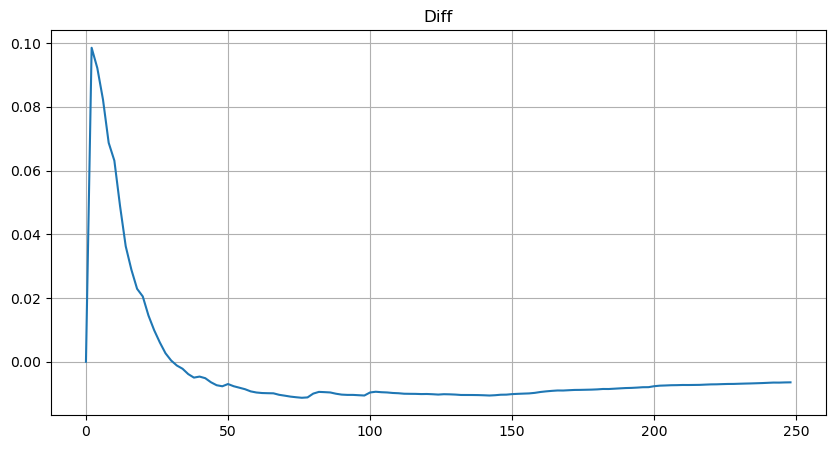
しかし、この推定値は見た目だけです。上の図では、シミュレーション値と実際の値の差をプロットしています。取引量が少ない場合、偏差は大きくなり、10%に近づくこともあります。パラメータ推定中に異なるポイントを選択することで、ポイントの確率をより正確にすることができますが、偏差の問題は解決されません。これはべき乗分布と実際の分布の差によって決まります。より正確な結果を得るためには、べき乗分布の式を修正する必要があります。具体的なプロセスについては詳しく説明しません。しかし、ひらめきがあり、実際には次のようになるはずだとわかりました。
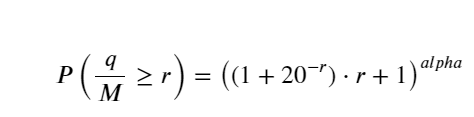
簡単にするために、ここでは標準化された取引量を表すために r = q/M を使用します。パラメータは上記と同じ方法で推定できます。下図は、補正後の最大偏差が2%を超えないことを示しています。理論上は補正を続けることもできますが、この精度で十分です。
depths = range(0, 250, 2)
probabilities = np.array([np.mean(buy_trades['quantity'] > depth) for depth in depths])
mean = buy_trades['quantity'].mean()
alpha = np.log(np.mean(buy_trades['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([(((1+20**(-depth/mean))*depth+mean)/mean)**alpha for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)
plt.figure(figsize=(10, 5))
plt.grid(True)
plt.title('Diff')
plt.plot(depths, probabilities_s-probabilities);
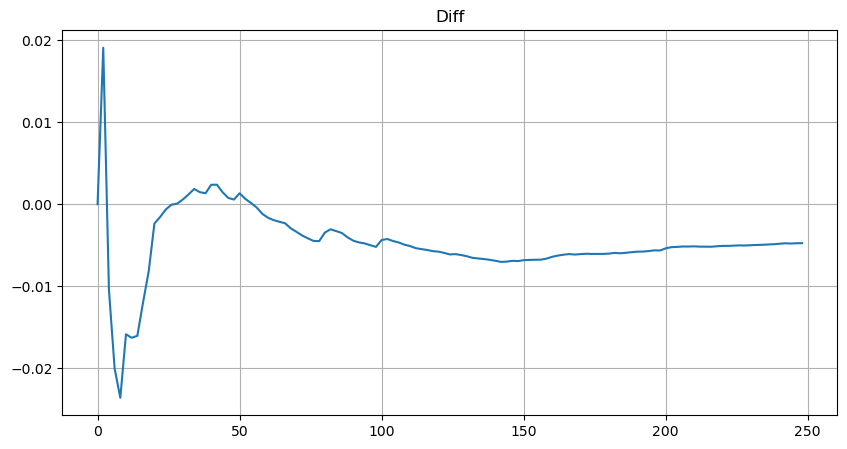
体積分布の推定方程式では、方程式の確率は真の確率ではなく条件付き確率であることに注意してください。この時点で、次の質問に答えることができます。次の順序が発生した場合、この順序が特定の値よりも大きくなる確率はどれくらいでしょうか?言い換えれば、異なる深さの注文が実行される確率はどれくらいかということです (理想的な状況、それほど厳密ではありませんが、理論的には注文簿には新しい注文とキャンセル、および同じ深さのキューがあります)。
この記事はこれでほぼ終わりですが、まだ答えなければならない質問が数多く残っています。次の一連の記事でその答えを提供していきたいと思います。