高頻度取引戦略についての考察(2)
 1
1
 3416
3416
この記事では、主に累積ボリュームモデリングと価格ショックに焦点を当てた高頻度取引戦略について説明します。本論文では、単一取引、固定間隔の価格ショック、取引量が価格に与える影響を分析し、予備的な最適注文配置モデルを提案します。このモデルは、ボリュームと価格ショックの理解に基づいて、最適な取引ポジションを見つけようとします。モデルの仮定については詳細に議論され、実際の期待収益とモデル予測による期待収益を比較することによって、最適な注文配置の予備評価が行われます。
累積ボリュームモデリング
前回の記事では、単一の取引量が特定の値を超える確率式を導出しました。
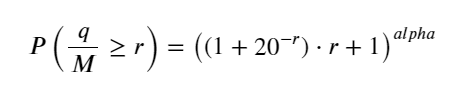
また、一定期間にわたる取引量の分布についても懸念されますが、これは直感的に各取引の量と注文頻度に関連しているはずです。次に、データは一定の間隔で処理されます。上記のようにその分布をプロットします。
from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
trades = pd.read_csv('HOOKUSDT-aggTrades-2023-01-27.csv')
trades['date'] = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index = trades['date']
buy_trades = trades[trades['is_buyer_maker']==False].copy()
buy_trades = buy_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
buy_trades['interval']=buy_trades['transact_time'] - buy_trades['transact_time'].shift()
buy_trades.index = buy_trades['date']
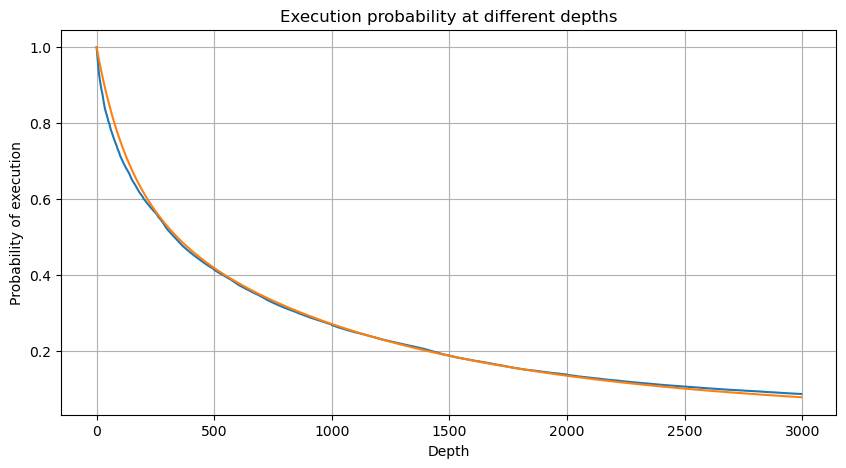
1秒ごとに取引量をマージし、取引が発生しなかった部分を削除し、上記の単一取引の分布を使用してフィットします。結果が良くなっていることがわかります。1秒以内のすべての取引を単一取引と見なすと、この問題は次のようになります。それは解決された問題となりました。ただし、サイクルが長くなると (トランザクション頻度に対して)、エラーが増加することが判明しており、このエラーは以前のパレート分布の修正項によって発生することが研究で判明しています。つまり、サイクルが長くなり、個々のトランザクションが増えるにつれて、複数のトランザクションの組み合わせがパレート分布に近づきます。この場合、修正項を削除する必要があります。
df_resampled = buy_trades['quantity'].resample('1S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
buy_trades
| agg_trade_id | price | quantity | first_trade_id | last_trade_id | is_buyer_maker | date | transact_time | interval | diff | |
|---|---|---|---|---|---|---|---|---|---|---|
| 2023-01-27 00:00:00.161 | 1138369 | 2.901 | 54.3 | 3806199 | 3806201 | False | 2023-01-27 00:00:00.161 | 1674777600161 | NaN | 0.001 |
| 2023-01-27 00:00:04.140 | 1138370 | 2.901 | 291.3 | 3806202 | 3806203 | False | 2023-01-27 00:00:04.140 | 1674777604140 | 3979.0 | 0.000 |
| 2023-01-27 00:00:04.339 | 1138373 | 2.902 | 55.1 | 3806205 | 3806207 | False | 2023-01-27 00:00:04.339 | 1674777604339 | 199.0 | 0.001 |
| 2023-01-27 00:00:04.772 | 1138374 | 2.902 | 1032.7 | 3806208 | 3806223 | False | 2023-01-27 00:00:04.772 | 1674777604772 | 433.0 | 0.000 |
| 2023-01-27 00:00:05.562 | 1138375 | 2.901 | 3.5 | 3806224 | 3806224 | False | 2023-01-27 00:00:05.562 | 1674777605562 | 790.0 | 0.000 |
| … | … | … | … | … | … | … | … | … | … | … |
| 2023-01-27 23:59:57.739 | 1544370 | 3.572 | 394.8 | 5074645 | 5074651 | False | 2023-01-27 23:59:57.739 | 1674863997739 | 1224.0 | 0.002 |
| 2023-01-27 23:59:57.902 | 1544372 | 3.573 | 177.6 | 5074652 | 5074655 | False | 2023-01-27 23:59:57.902 | 1674863997902 | 163.0 | 0.001 |
| 2023-01-27 23:59:58.107 | 1544373 | 3.573 | 139.8 | 5074656 | 5074656 | False | 2023-01-27 23:59:58.107 | 1674863998107 | 205.0 | 0.000 |
| 2023-01-27 23:59:58.302 | 1544374 | 3.573 | 60.5 | 5074657 | 5074657 | False | 2023-01-27 23:59:58.302 | 1674863998302 | 195.0 | 0.000 |
| 2023-01-27 23:59:59.894 | 1544376 | 3.571 | 12.1 | 5074662 | 5074664 | False | 2023-01-27 23:59:59.894 | 1674863999894 | 1592.0 | 0.000 |
#1s内的累计分布
depths = np.array(range(0, 3000, 5))
probabilities = np.array([np.mean(df_resampled['quantity'] > depth) for depth in depths])
mean = df_resampled['quantity'].mean()
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([((1+20**(-depth/mean))*depth/mean+1)**(alpha) for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)
df_resampled = buy_trades['quantity'].resample('30S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
depths = np.array(range(0, 12000, 20))
probabilities = np.array([np.mean(df_resampled['quantity'] > depth) for depth in depths])
mean = df_resampled['quantity'].mean()
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([((1+20**(-depth/mean))*depth/mean+1)**(alpha) for depth in depths])
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2)
probabilities_s_2 = np.array([(depth/mean+1)**alpha for depth in depths]) # 无修正
plt.figure(figsize=(10, 5))
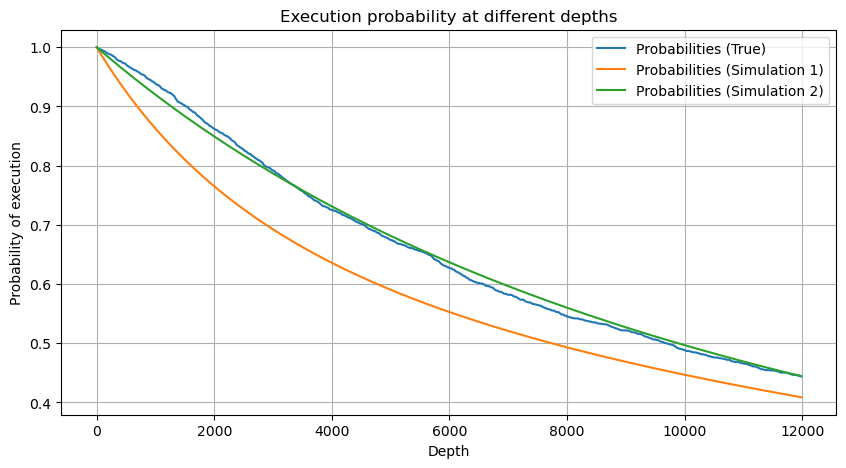
plt.plot(depths, probabilities,label='Probabilities (True)')
plt.plot(depths, probabilities_s, label='Probabilities (Simulation 1)')
plt.plot(depths, probabilities_s_2, label='Probabilities (Simulation 2)')
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.legend()
plt.grid(True)
これで、異なる時間における累積取引量の分布の一般的な公式をまとめ、その公式に単一取引の分布を当てはめることができました。これにより、毎回個別に取引量をカウントする必要がなくなりました。ここではプロセスを省略し、式を直接示します。
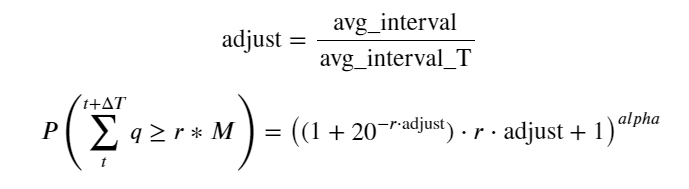
このうち、avg_interval は単一トランザクション間の平均間隔を表し、avg_interval_T は推定する必要のある間隔の平均間隔を表します。少しわかりにくいです。 1 秒のトランザクション時間を推定する場合は、1 秒以内のトランザクションを含むイベント間の平均間隔を計算する必要があります。注文が到着する確率がポアソン分布に従う場合は、ここで直接推定できるはずですが、実際の偏差は大きいため、ここでは説明しません。
一定期間内にボリュームが一定値を超える確率は、そのポジションでの取引の実際の確率とはかなり異なることに注意してください。待機時間が長いほど、注文書が閉じられる可能性が高くなるためです。変化し、トランザクションも深度が変化するため、データが更新されるたびに同じ深度位置でのトランザクション確率がリアルタイムに変化します。
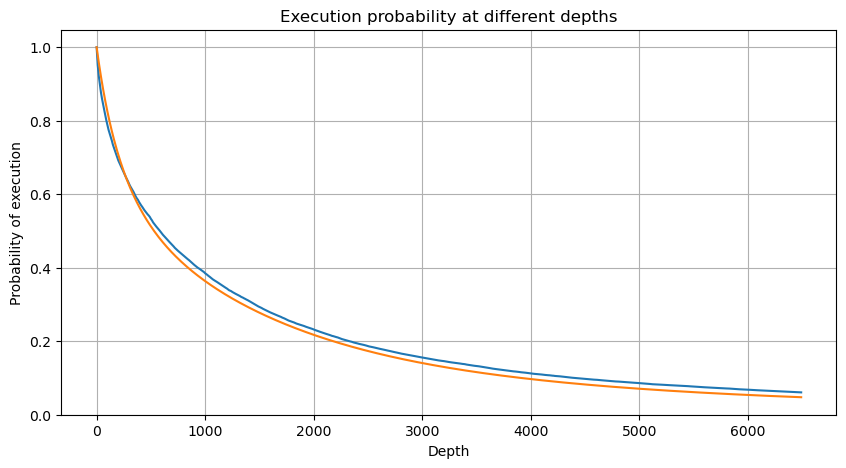
df_resampled = buy_trades['quantity'].resample('2S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
depths = np.array(range(0, 6500, 10))
probabilities = np.array([np.mean(df_resampled['quantity'] > depth) for depth in depths])
mean = buy_trades['quantity'].mean()
adjust = buy_trades['interval'].mean() / 2620
alpha = np.log(np.mean(buy_trades['quantity'] > mean))/0.7178397931503168
probabilities_s = np.array([((1+20**(-depth*adjust/mean))*depth*adjust/mean+1)**(alpha) for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)
単一取引の価格影響
取引データは宝であり、まだ採掘すべきデータが大量に存在します。注文が価格に与える影響には細心の注意を払う必要があります。これは戦略における保留中の注文の配置に影響します。同様に、transact_time 集計データに基づいて、最終価格と最初の価格の差を計算します。注文が 1 つしかない場合、差は 0 になります。不思議なのは、否定的な結果を示すデータ結果がまだ少数あることです。これはデータの配置順序の問題であるはずなので、ここでは触れません。
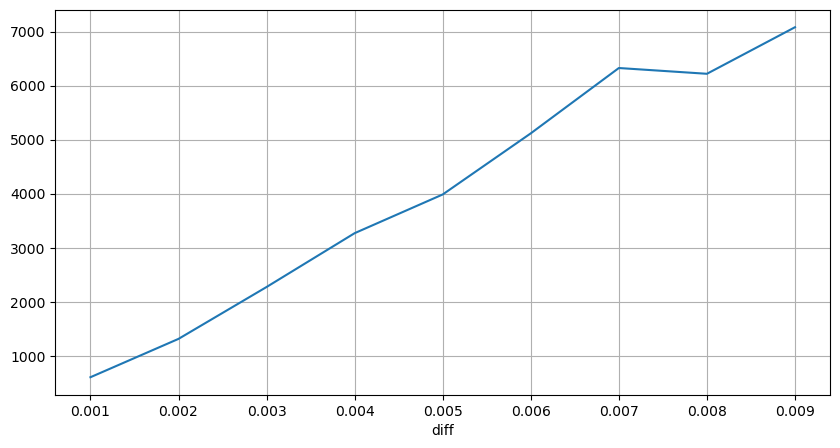
結果によると、影響なしの割合は77%と高く、1ティックの割合は16.5%、2ティックは3.7%、3ティックは1.2%、4ティック以上の割合は1%未満でした。 。これは基本的に指数関数の特性に準拠していますが、フィッティングは正確ではありません。
対応する価格差を生じさせた取引量をカウントし、影響が大きすぎることによる歪みを除去しました。基本的には線形関係に従い、約1,000取引量ごとに1ティックの価格変動が生じます。また、各価格付近の保留注文の平均数は約 1,000 件であることもわかります。
diff_df = trades[trades['is_buyer_maker']==False].groupby('transact_time')['price'].agg(lambda x: abs(round(x.iloc[-1] - x.iloc[0],3)) if len(x) > 1 else 0)
buy_trades['diff'] = buy_trades['transact_time'].map(diff_df)
diff_counts = buy_trades['diff'].value_counts()
diff_counts[diff_counts>10]/diff_counts.sum()
0.000 0.769965
0.001 0.165527
0.002 0.037826
0.003 0.012546
0.004 0.005986
0.005 0.003173
0.006 0.001964
0.007 0.001036
0.008 0.000795
0.009 0.000474
0.010 0.000227
0.011 0.000187
0.012 0.000087
0.013 0.000080
Name: diff, dtype: float64
diff_group = buy_trades.groupby('diff').agg({
'quantity': 'mean',
'diff': 'last',
})
diff_group['quantity'][diff_group['diff']>0][diff_group['diff']<0.01].plot(figsize=(10,5),grid=True);
定期的に起こる価格ショック
2 秒以内の価格の影響をカウントします。ここでの違いは、負の値があることです。もちろん、ここでは買い注文のみがカウントされるため、対称的なポジションは 1 ティック大きくなります。取引量と影響度の関係を引き続き観察し、0 より大きい結果のみをカウントします。結論は単一注文の場合と同様で、これも近似線形関係です。各ティックには約 2000 ボリュームが必要です。
df_resampled = buy_trades.resample('2S').agg({
'price': ['first', 'last', 'count'],
'quantity': 'sum'
})
df_resampled['price_diff'] = round(df_resampled[('price', 'last')] - df_resampled[('price', 'first')],3)
df_resampled['price_diff'] = df_resampled['price_diff'].fillna(0)
result_df_raw = pd.DataFrame({
'price_diff': df_resampled['price_diff'],
'quantity_sum': df_resampled[('quantity', 'sum')],
'data_count': df_resampled[('price', 'count')]
})
result_df = result_df_raw[result_df_raw['price_diff'] != 0]
result_df['price_diff'][abs(result_df['price_diff'])<0.016].value_counts().sort_index().plot.bar(figsize=(10,5));
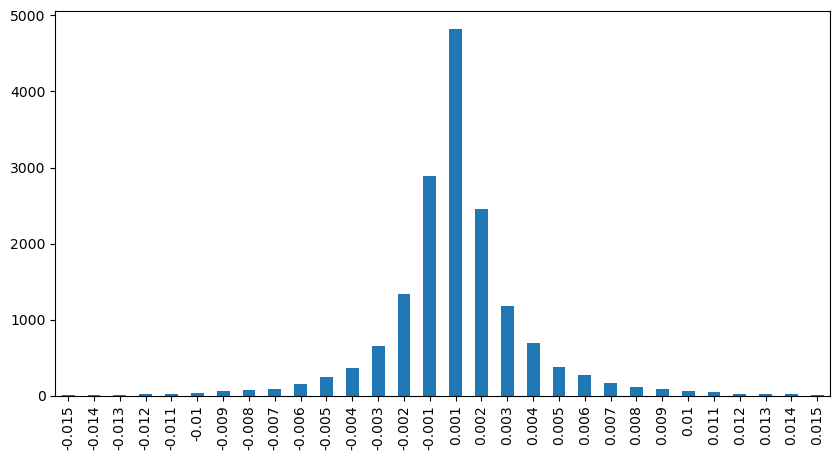
result_df['price_diff'].value_counts()[result_df['price_diff'].value_counts()>30]
0.001 7176
-0.001 3665
0.002 3069
-0.002 1536
0.003 1260
0.004 692
-0.003 608
0.005 391
-0.004 322
0.006 259
-0.005 192
0.007 146
-0.006 112
0.008 82
0.009 75
-0.007 75
-0.008 65
0.010 51
0.011 41
-0.010 31
Name: price_diff, dtype: int64
diff_group = result_df.groupby('price_diff').agg({ 'quantity_sum': 'mean'})
diff_group[(diff_group.index>0) & (diff_group.index<0.015)].plot(figsize=(10,5),grid=True);
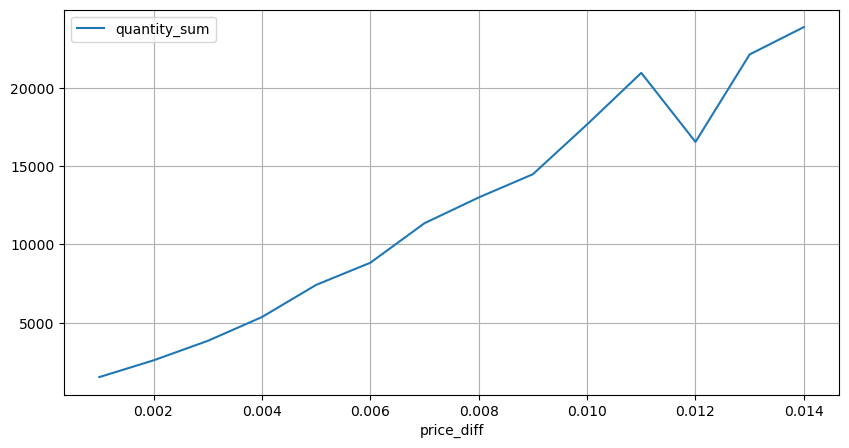
数量による価格への影響
ティック変更に必要なボリュームは以前に計算されましたが、影響がすでに発生しているという仮定に基づいているため、正確ではありません。それでは、取引量による価格への影響を見てみましょう。
ここでのデータは 1 秒ごとにサンプリングされ、100 数量を 1 ステップとして、この数量範囲内での価格の変化がカウントされます。いくつかの貴重な結論が導き出されました。
- 購入量が 500 を下回ると、価格に影響を与える売り注文もあるため、予想される価格変動は減少します。
- 取引量が少ない場合は、取引量が増えるほど価格の上昇も大きくなるという直線関係に従います。
- 買い注文量が大きいほど、価格変動が大きくなり、多くの場合、価格のブレイクスルーを表します。ブレイクスルー後、価格は戻る可能性があります。固定間隔でのサンプリングと相まって、データは不安定です。
- 散布図の上部、つまり、ボリュームが価格の上昇に対応する部分に注意を払う必要があります。
- この取引ペアについてのみ、取引量と価格変動の関係の大まかなバージョンが示されています。
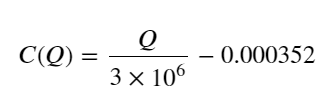
このうち、「C」は価格の変化を表し、「Q」は買い注文量を表します。
df_resampled = buy_trades.resample('1S').agg({
'price': ['first', 'last', 'count'],
'quantity': 'sum'
})
df_resampled['price_diff'] = round(df_resampled[('price', 'last')] - df_resampled[('price', 'first')],3)
df_resampled['price_diff'] = df_resampled['price_diff'].fillna(0)
result_df_raw = pd.DataFrame({
'price_diff': df_resampled['price_diff'],
'quantity_sum': df_resampled[('quantity', 'sum')],
'data_count': df_resampled[('price', 'count')]
})
result_df = result_df_raw[result_df_raw['price_diff'] != 0]
df = result_df.copy()
bins = np.arange(0, 30000, 100) #
labels = [f'{i}-{i+100-1}' for i in bins[:-1]]
df.loc[:, 'quantity_group'] = pd.cut(df['quantity_sum'], bins=bins, labels=labels)
grouped = df.groupby('quantity_group')['price_diff'].mean()
grouped_df = pd.DataFrame(grouped).reset_index()
grouped_df['quantity_group_center'] = grouped_df['quantity_group'].apply(lambda x: (float(x.split('-')[0]) + float(x.split('-')[1])) / 2)
plt.figure(figsize=(10,5))
plt.scatter(grouped_df['quantity_group_center'], grouped_df['price_diff'],s=10)
plt.plot(grouped_df['quantity_group_center'], np.array(grouped_df['quantity_group_center'].values)/2e6-0.000352,color='red')
plt.xlabel('quantity_group_center')
plt.ylabel('average price_diff')
plt.title('Scatter plot of average price_diff by quantity_group')
plt.grid(True)
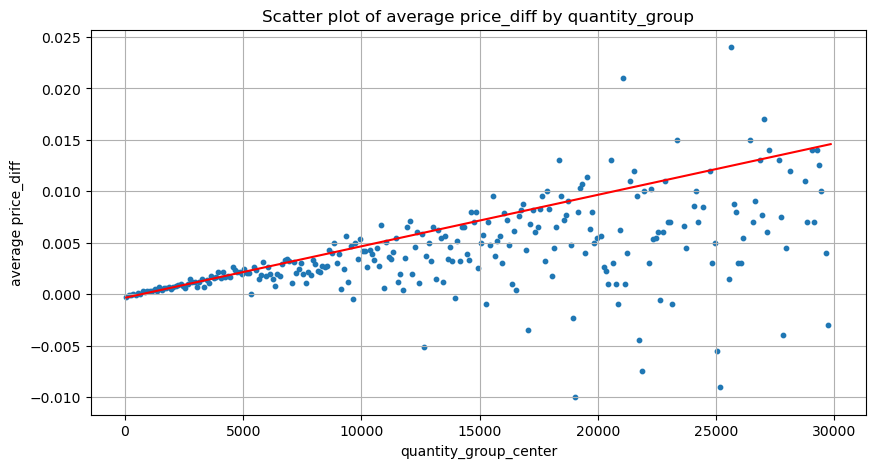
grouped_df.head(10)
| quantity_group | price_diff | quantity_group_center | |
|---|---|---|---|
| 0 | 0-199 | -0.000302 | 99.5 |
| 1 | 100-299 | -0.000124 | 199.5 |
| 2 | 200-399 | -0.000068 | 299.5 |
| 3 | 300-499 | -0.000017 | 399.5 |
| 4 | 400-599 | -0.000048 | 499.5 |
| 5 | 500-699 | 0.000098 | 599.5 |
| 6 | 600-799 | 0.000006 | 699.5 |
| 7 | 700-899 | 0.000261 | 799.5 |
| 8 | 800-999 | 0.000186 | 899.5 |
| 9 | 900-1099 | 0.000299 | 999.5 |
初期最適注文位置
取引量のモデリングと価格影響度に対応した取引量の大まかなモデルにより、最適な注文ポジションを計算できるようです。いくつかの仮定を立てて、無責任な最適価格の位置を示してみましょう。
- ショック後に価格が元の値に戻ると仮定します(もちろんこれはありそうにないので、ショック後の価格変動の再分析が必要です)
- この期間中の取引量と注文頻度の分布が、事前に設定された要件を満たしていると仮定します (推定には 1 日の値が使用され、取引には明らかなクラスタリングがあるため、これも不正確です)。
- シミュレーション時間中に売り注文が 1 つだけ発生し、その後ポジションがクローズされると仮定します。
- 注文が実行された後、特に取引量が非常に少ない場合に、価格を押し上げ続ける他の買い注文があると仮定します。この影響はここでは無視され、単に価格が戻ると想定されます。
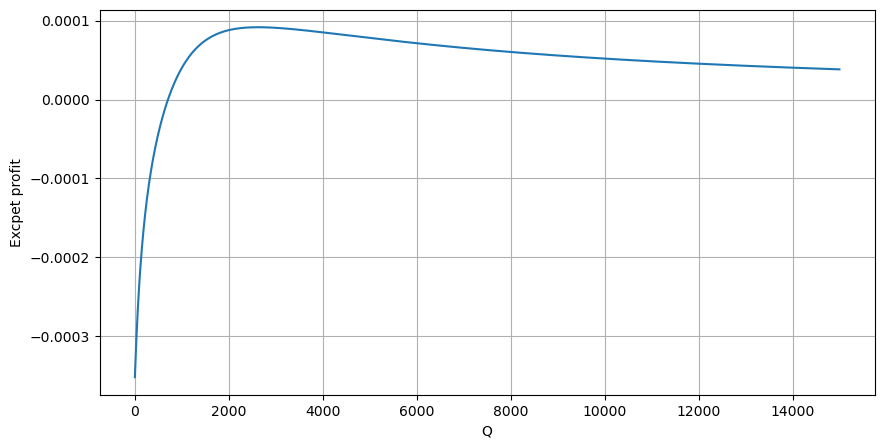
まず、単純な期待収益、つまり累積買い注文が 1 秒以内に Q を超える確率に期待収益率 (つまり、インパクト価格) を掛けたものを書き出します。
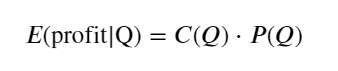
グラフによれば、期待収益は平均取引量の約2.5倍である2500付近で最大となります。つまり、売り注文は 2500 で出す必要があります。水平軸は 1 秒以内の取引量を表しており、単純に深度位置と同一視することはできないことを再度強調する必要があります。そして、これは非常に重要な詳細なデータがまだ不足している時期であり、取引に基づく推測のみに基づいています。
要約する
異なる時間間隔でのボリューム分布は、単一のトランザクションのボリューム分布の単純なスケーリングであることがわかります。また、価格ショックと取引確率に基づいた単純な期待収益モデルも作成しました。このモデルの結果は私たちの予想と一致しています。売り注文の数量が少ない場合は、価格が下落していることを示しています。利益率があり、取引量が多いほど利益率は高くなります。確率が大きいほど、利益率は低くなります。中間に最適なサイズがあり、それが戦略が求めている注文配置位置でもあります。もちろん、このモデルはまだ単純すぎます。次の記事では、さらに詳しく説明します。
#1s内的累计分布
df_resampled = buy_trades['quantity'].resample('1S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
depths = np.array(range(0, 15000, 10))
mean = df_resampled['quantity'].mean()
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([((1+20**(-depth/mean))*depth/mean+1)**(alpha) for depth in depths])
profit_s = np.array([depth/2e6-0.000352 for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities_s*profit_s)
plt.xlabel('Q')
plt.ylabel('Excpet profit')
plt.grid(True)