前回の記事では、注文到着間隔を調査し、パラメータを動的に調整する必要がある理由と、見積りの品質を評価する方法について説明しました。この記事では、詳細なデータに焦点を当て、中間価格（公正価格、マイクロ価格などとも呼ばれます）を調査します。

深度データ

Binanceは、best_bid_price: 最高入札価格、つまり最高入札価格、best_bid_qty: 最高入札価格の数、best_ask_price: 最高売り値、best_ask_qty: 最高売り値の数を含む、最高相場の履歴データのダウンロードを提供します。 、transaction_time: タイムスタンプ。このデータには、第 2 レベルおよびそれより深いレベルの保留中の注文は含まれません。ここで分析する市場状況は、8月7日のYGGです。当日の市場変動は非常に激しく、データ量は900万以上に達しました。

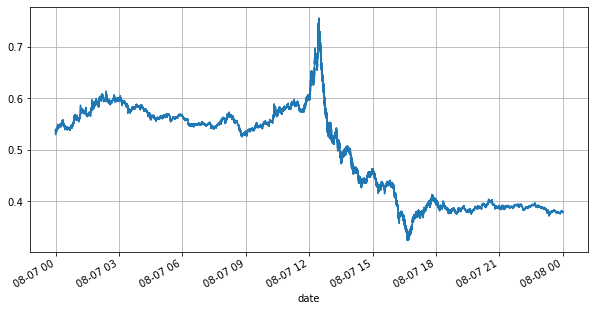
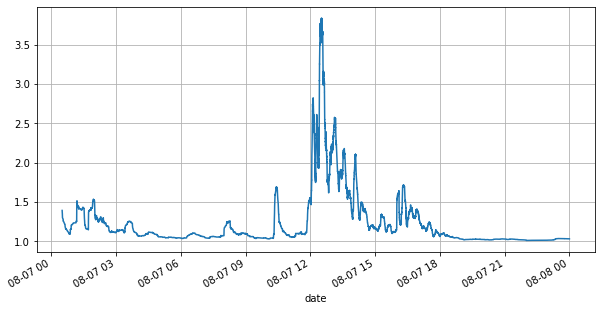
まず、当日の相場を見てみましょう。相場は大きく上下しています。また、当日の未決注文数も相場の変動とともに大きく変化しています。特に、スプレッド（売値と買値の差は市場の変動状況を大きく表しています。当日のYGG市場の統計によると、スプレッドが1ティックを超える時間の割合は20％でした。さまざまなロボットが市場で競争しているこの時代に、このような状況はまれです。

from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

books = pd.read_csv('YGGUSDT-bookTicker-2023-08-07.csv')

tick_size = 0.0001

books['date'] = pd.to_datetime(books['transaction_time'], unit='ms')
books.index = books['date']

books['spread'] = round(books['best_ask_price'] - books['best_bid_price'],4)

books['best_bid_price'][::10].plot(figsize=(10,5),grid=True);

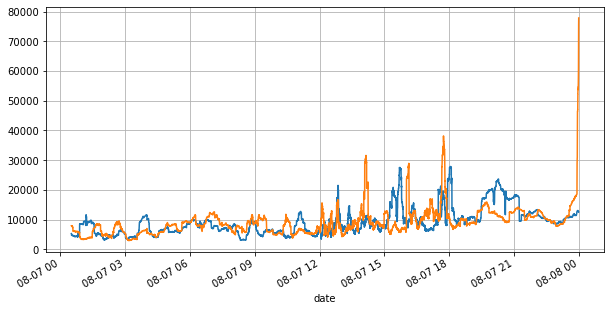
books['best_bid_qty'][::10].rolling(10000).mean().plot(figsize=(10,5),grid=True);
books['best_ask_qty'][::10].rolling(10000).mean().plot(figsize=(10,5),grid=True);

(books['spread'][::10]/tick_size).rolling(10000).mean().plot(figsize=(10,5),grid=True);

books['spread'].value_counts()[books['spread'].value_counts()>500]/books['spread'].value_counts().sum()

0.0001    0.799169
0.0002    0.102750
0.0003    0.042472
0.0004    0.022821
0.0005    0.012792
0.0006    0.007350
0.0007    0.004376
0.0008    0.002712
0.0009    0.001657
0.0010    0.001089
0.0011    0.000740
0.0012    0.000496
0.0013    0.000380
0.0014    0.000258
0.0015    0.000197
0.0016    0.000140
0.0017    0.000112
0.0018    0.000088
0.0019    0.000063
Name: spread, dtype: float64

不均衡な引用

上記から、買い注文と売り注文の量はほとんどの場合大きく異なることがわかります。この違いは、短期的な市場状況に強い予測効果をもたらします。その理由は、前回の記事で述べた、小口の買い注文が下落につながることが多いという理由と似ています。一方の保留注文がもう一方の保留注文よりも大幅に小さく、アクティブな買い注文と売り注文の量が近いと仮定すると、保留注文の少ない側が消化される可能性が高くなり、価格が上昇する。変更。非対称の引用符は I で表されます。 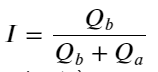ここで、Q_b は買い注文数量 (best_bid_qty) を表し、Q_a は売り注文数量 (best_ask_qty) を表します。

中間価格を定義する: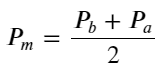

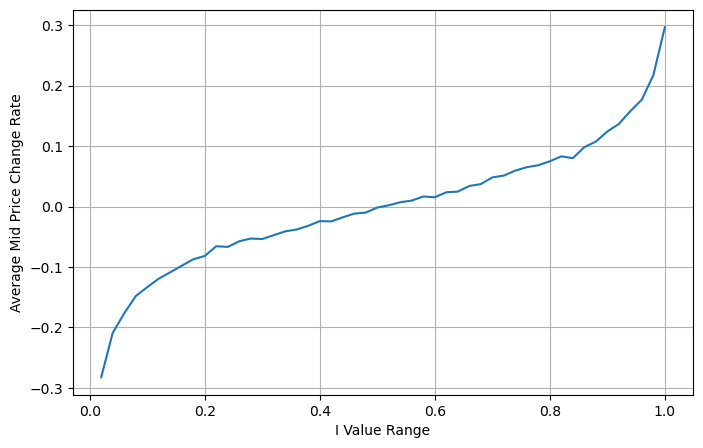
次の図は、次の区間の中間価格の変化率と不均衡Iの関係を示しています。予想どおり、Iが増加すると価格が上昇する可能性が高くなり、1に近づくほど、価格変動も加速しています。高頻度取引において、仲値を導入する目的は、将来の価格変動をより正確に予測することです。言い換えれば、将来の価格との差が小さいほど、仲値はより適切に定義されます。明らかに、保留中の注文の不均衡は戦略の予測に追加情報を提供します。これを考慮して、加重中間価格を定義します。

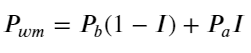
books['I'] = books['best_bid_qty'] / (books['best_bid_qty'] + books['best_ask_qty'])

books['mid_price'] = (books['best_ask_price'] + books['best_bid_price'])/2

bins = np.linspace(0, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['price_change'] = (books['mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['price_change'].mean()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Average Mid Price Change Rate');
plt.grid(True)

books['weighted_mid_price'] = books['mid_price'] + books['spread']*books['I']/2
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['weighted_price_change'] = (books['weighted_mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['weighted_price_change'].mean()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

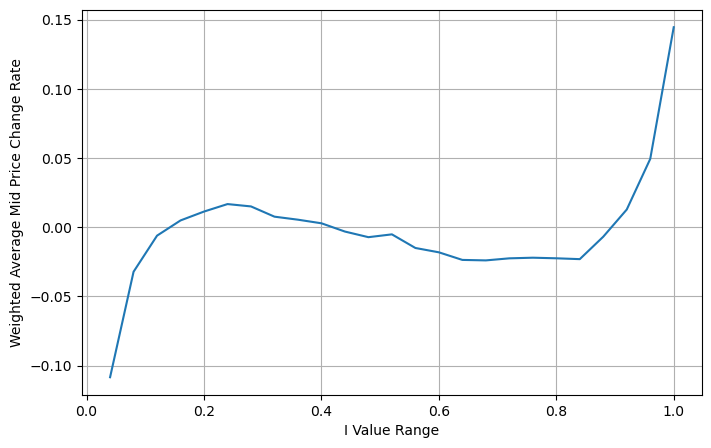
加重仲値調整

図から、加重中間価格の変化は異なる I の変化よりもはるかに少ないことがわかります。これは、加重中間価格の方が適合性が高いことを意味します。しかし、偏差が比較的大きい 0.2 や 0.8 付近など、いくつかの規則性はまだ残っています。これは、私がまだ追加情報を提供できることを示しています。加重平均価格は価格修正項がIと完全に線形であると仮定しているため、これは明らかに真実ではない。上の図からわかるように、Iが0と1に近い場合、偏差はより速く、線形関係。

より直感的にわかるように、I はここで再定義されます。

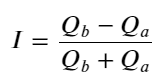
現時点では：

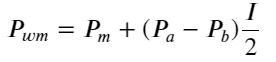
この形式を見ると、加重中間価格は平均中間価格の修正であることがわかります。修正項の係数はスプレッドであり、修正項はIの関数です。加重中間価格は、単純に次のことを前提としています。この関係はI/2です。このとき、I(-1,1)の調整分布の利点が反映されます。Iは原点を中心に対称であるため、関数のフィッティング関係を見つけるのに便利です。グラフを見ると、この関数はIの奇数乗の関係を満たしているはずであり、これは両辺の急速な増加と原点周りの対称性と一致する。さらに、原点付近の値は線形に近いことが分かる。 I が 0 の場合、関数の結果は 0 になり、I が 1 の場合、関数の結果は 0.5 になります。したがって、この関数は次のようになります。

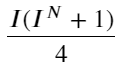
ここで、N は正の偶数です。実際のテストでは、N が 8 のほうが良いことがわかりました。これまでのところ、この記事では改訂された加重中間価格を提案しています。

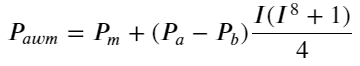
この時点では、予測される中間価格の変化は基本的に I とは何の関係もありません。この結果は単純な加重仲値よりも優れていますが、実際の取引には適用できません。これはここで提示された単なるアイデアです。 2017年のS・ストイコフの論文ではマルコフ連鎖法が紹介された。Micro-Price、関連コードも記載されているので、勉強することもできます。

books['I'] = (books['best_bid_qty'] - books['best_ask_qty']) / (books['best_bid_qty'] + books['best_ask_qty'])

books['weighted_mid_price'] = books['mid_price'] + books['spread']*books['I']/2
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['weighted_price_change'] = (books['weighted_mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['weighted_price_change'].sum()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

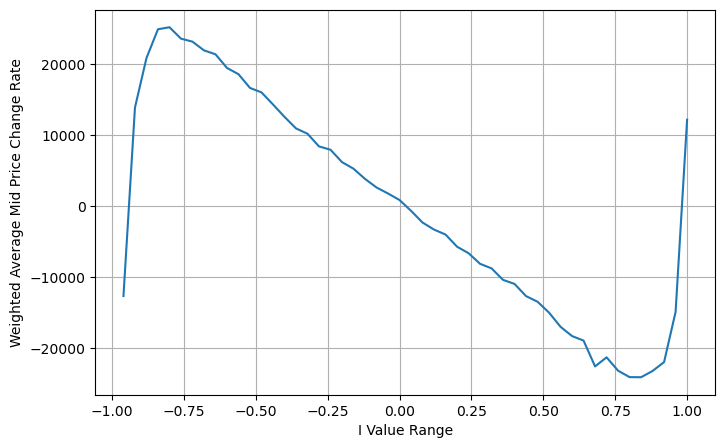
books['adjust_mid_price'] = books['mid_price'] + books['spread']*(books['I'])*(books['I']**8+1)/4
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['adjust_mid_price'] = (books['adjust_mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['adjust_mid_price'].sum()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

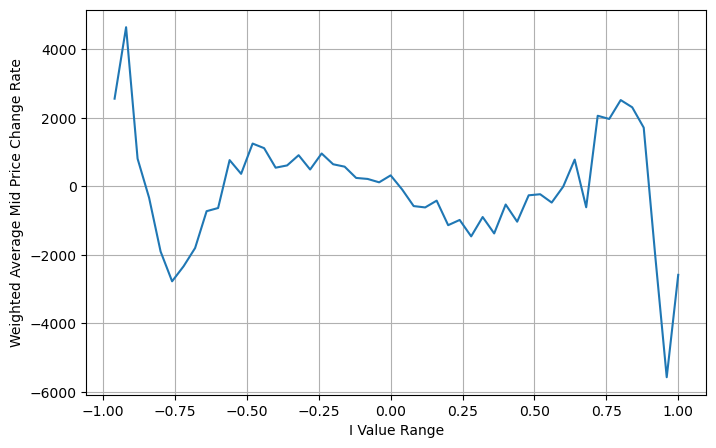
books['adjust_mid_price'] = books['mid_price'] + books['spread']*(books['I']**3)/2
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['adjust_mid_price'] = (books['adjust_mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['adjust_mid_price'].sum()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

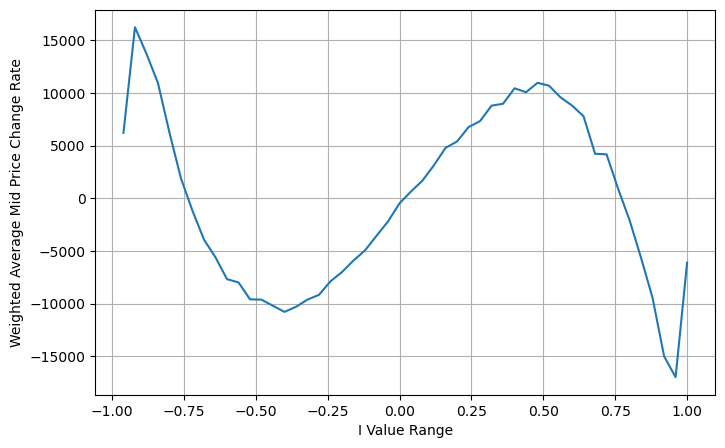
要約する

高頻度戦略では、中間価格が非常に重要です。中間価格は将来の短期価格の予測であるため、中間価格は可能な限り正確でなければなりません。分析では 1 つの市場価格のみが使用されるため、上記で紹介した中間価格はすべて市場データに基づいています。実際の取引では、特に実際の取引で取引交換がある場合、戦略は可能な限りすべてのデータを使用し、仲値の予測は実際の取引価格でテストする必要があります。ストイコフ氏が、実際の中間価格は、買い・売り取引の確率の加重平均であるべきだというツイートを投稿したように記憶しています。この問題は、前回の記事で検討したばかりです。スペースが限られているため、これらの問題については次の記事で詳しく説明します。