이전 기사에서는 주문 도착 간격을 조사하고 매개변수를 동적으로 조정해야 하는 이유와 추정의 품질을 평가하는 방법을 설명했습니다. 이 글에서는 심층적인 데이터에 초점을 맞추고 중간 가격(공정 가격, 미시 가격 등이라고도 함)을 연구합니다.

깊이 데이터

Binance는 best_bid_price: 최고 입찰 가격, 즉 최대 입찰 가격, best_bid_qty: 최고 입찰 가격의 수, best_ask_price: 최고 매도 가격, best_ask_qty: 최고 매도 가격의 수를 포함하여 최고 호가의 과거 데이터 다운로드를 제공합니다. , transaction_time: 타임스탬프. 이 데이터에는 2단계 및 더 깊은 보류 주문은 포함되지 않습니다. 여기서 분석한 시장 상황은 8월 7일 YGG입니다. 그날 시장 변동은 매우 극심했고 데이터 양은 900만 개가 넘었습니다.

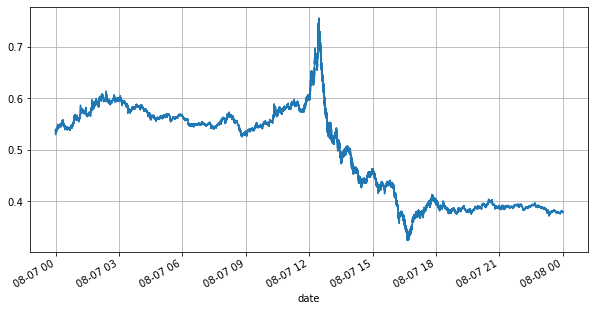
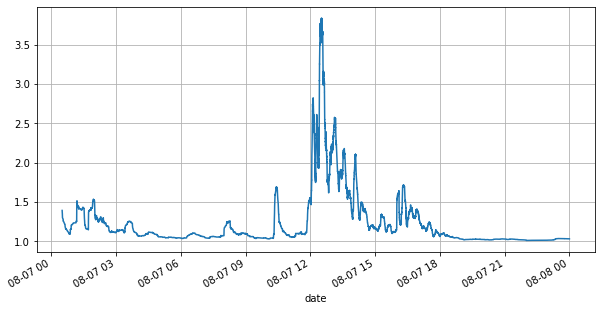
먼저 당일 시장을 살펴보겠습니다. 엄청난 기복이 있습니다. 게다가 당일 보류 주문 수도 시장의 변동에 따라 크게 변했습니다. 특히 스프레드( 판매 가격과 매수 가격)은 시장의 변동 상황을 뚜렷하게 보여줍니다. 그날 YGG의 시장 통계에 따르면, 스프레드가 1틱 이상인 경우가 20%였습니다. 다양한 로봇이 시장에서 경쟁하는 이 시대에 이런 상황은 드뭅니다.

from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

books = pd.read_csv('YGGUSDT-bookTicker-2023-08-07.csv')

tick_size = 0.0001

books['date'] = pd.to_datetime(books['transaction_time'], unit='ms')
books.index = books['date']

books['spread'] = round(books['best_ask_price'] - books['best_bid_price'],4)

books['best_bid_price'][::10].plot(figsize=(10,5),grid=True);

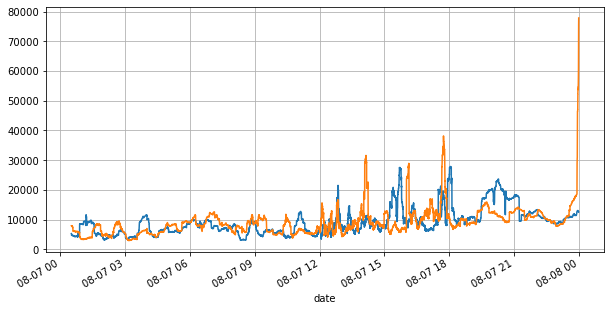
books['best_bid_qty'][::10].rolling(10000).mean().plot(figsize=(10,5),grid=True);
books['best_ask_qty'][::10].rolling(10000).mean().plot(figsize=(10,5),grid=True);

(books['spread'][::10]/tick_size).rolling(10000).mean().plot(figsize=(10,5),grid=True);

books['spread'].value_counts()[books['spread'].value_counts()>500]/books['spread'].value_counts().sum()

0.0001    0.799169
0.0002    0.102750
0.0003    0.042472
0.0004    0.022821
0.0005    0.012792
0.0006    0.007350
0.0007    0.004376
0.0008    0.002712
0.0009    0.001657
0.0010    0.001089
0.0011    0.000740
0.0012    0.000496
0.0013    0.000380
0.0014    0.000258
0.0015    0.000197
0.0016    0.000140
0.0017    0.000112
0.0018    0.000088
0.0019    0.000063
Name: spread, dtype: float64

불균형한 인용문

위에서 볼 수 있듯이, 매수 및 매도 주문의 양은 대부분 매우 다릅니다. 이 차이는 단기 시장 상황에 강력한 예측 효과를 미칩니다. 그 이유는 이전 기사에서 언급한 이유와 비슷한데, 소액 매수 주문이 종종 하락으로 이어지는 것입니다. 한 쪽의 보류 주문이 다른 쪽의 보류 주문보다 훨씬 적고 활성 매수 및 매도 주문의 볼륨이 가깝다고 가정하면 보류 주문이 작은 쪽이 잠식될 가능성이 더 높아 가격이 상승합니다. 변화. 불균형한 견적은 I로 표시됩니다. 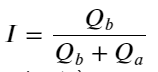여기서 Q_b는 매수 주문 수량(best_bid_qty)을 나타내고, Q_a는 매도 주문 수량(best_ask_qty)을 나타냅니다.

중간 가격 정의: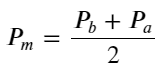

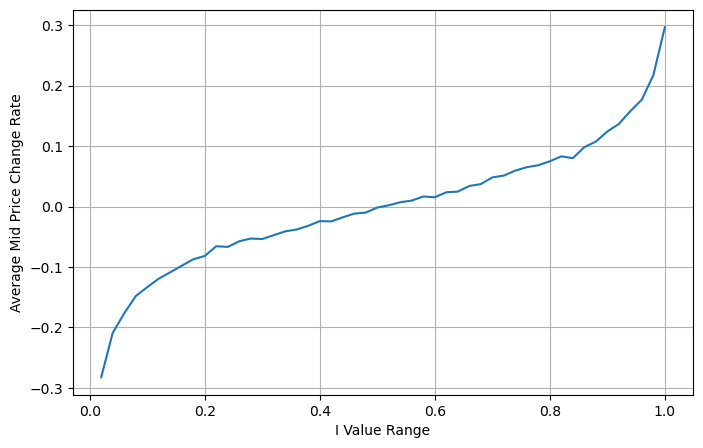
다음 그림은 다음 구간의 중간가격 변화율과 불균형 I의 관계를 보여준다. 예상대로 I가 증가할수록 가격이 상승할 가능성이 높아지고 1에 가까울수록 불균형의 크기가 커진다. 가격 변화도 가속화됩니다. 고빈도 거래에서 중간 가격을 도입하는 목적은 미래의 가격 변화를 더 잘 예측하는 것입니다. 즉, 미래 가격과의 차이가 작을수록 중간 가격이 더 잘 정의됩니다. 분명히 보류 중인 주문의 불균형은 전략 예측에 대한 추가 정보를 제공합니다. 이를 고려하여 가중 중간 가격을 정의합니다.

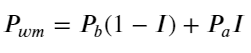
books['I'] = books['best_bid_qty'] / (books['best_bid_qty'] + books['best_ask_qty'])

books['mid_price'] = (books['best_ask_price'] + books['best_bid_price'])/2

bins = np.linspace(0, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['price_change'] = (books['mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['price_change'].mean()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Average Mid Price Change Rate');
plt.grid(True)

books['weighted_mid_price'] = books['mid_price'] + books['spread']*books['I']/2
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['weighted_price_change'] = (books['weighted_mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['weighted_price_change'].mean()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

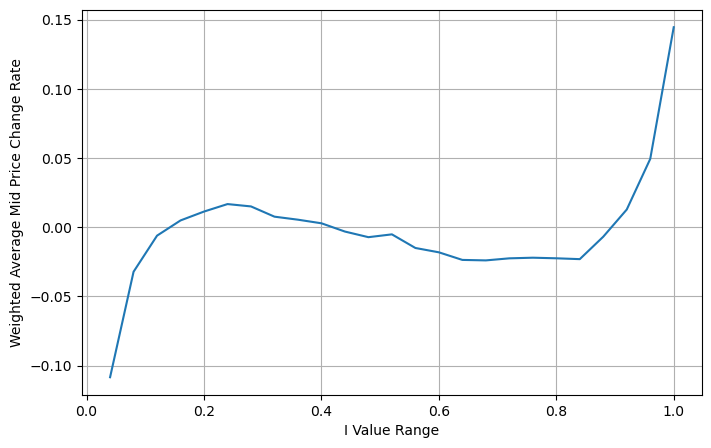
가중 중간 가격 조정

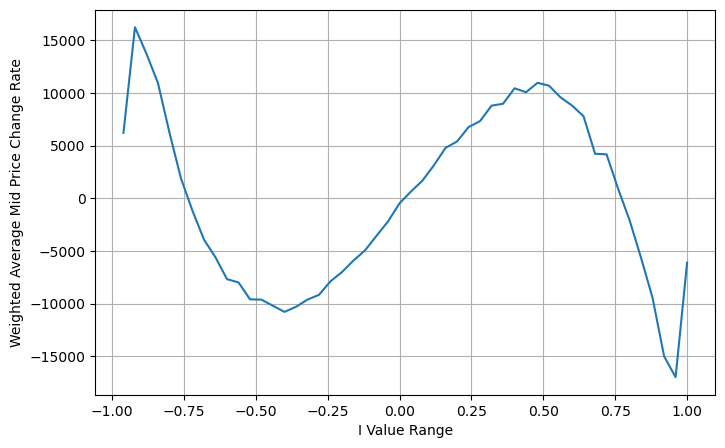
그림에서 볼 수 있듯이 가중 중간 가격은 다른 I보다 훨씬 적게 변합니다. 즉, 가중 중간 가격이 더 잘 맞는다는 것을 알 수 있습니다. 그러나 0.2와 0.8 정도의 편차가 비교적 큰 규칙적인 경우도 여전히 존재합니다. 이는 제가 여전히 추가 정보를 제공할 수 있음을 보여줍니다. 가중 중간 가격은 가격 수정 항이 I와 완전히 선형이라고 가정하기 때문에 이는 분명히 사실이 아닙니다. 위 그림에서 볼 수 있듯이 I가 0과 1에 가까울 때 편차가 더 빠르고 선형 관계

좀 더 직관적으로 보기 위해 I를 여기에 다시 정의했습니다.

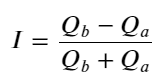
이 시간에는:

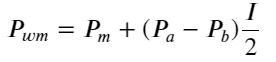
이 형태를 관찰하면 가중 중간 가격이 평균 중간 가격에 대한 수정이라는 것을 알 수 있습니다. 수정 항의 계수는 Spread이고 수정 항은 I의 함수입니다. 가중 중간 가격은 단순히 다음을 가정합니다. 이 관계는 I/2입니다. 이때, I(-1,1)의 조정된 분포의 이점이 반영됩니다. I는 원점에 대해 대칭이므로 함수의 적합 관계를 찾는 것이 편리합니다. 그래프를 관찰하면, 이 함수는 I의 홀수 거듭제곱 관계를 만족해야 하는데, 이는 양쪽의 빠른 성장과 원점에 대한 대칭성과 일치합니다. 또한, 원점 근처의 값이 선형에 가깝다는 것을 관찰할 수 있습니다. 그리고 I가 0일 때, 함수의 결과는 0이고, I가 1일 때, 함수의 결과는 0.5입니다. 그러므로 이 함수는 다음과 같습니다.

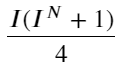
여기서 N은 양의 짝수입니다. 실제 테스트 후 N이 8일 때 더 좋습니다. 지금까지 이 기사에서는 개정된 가중 중간 가격을 제안합니다.

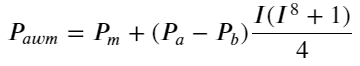
이 시점에서 예측된 중간 가격의 변화는 기본적으로 I와 아무런 관련이 없습니다. 이 결과는 단순 가중 중간 가격보다 나았지만 실제 거래에 적용할 수는 없습니다. 여기서는 단지 아이디어일 뿐입니다. 2017년 S Stoikov의 기사에서 마르코프 체인 방법이 소개되었습니다.Micro-Price, 관련 코드를 제공하므로, 이를 공부할 수도 있습니다.

books['I'] = (books['best_bid_qty'] - books['best_ask_qty']) / (books['best_bid_qty'] + books['best_ask_qty'])

books['weighted_mid_price'] = books['mid_price'] + books['spread']*books['I']/2
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['weighted_price_change'] = (books['weighted_mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['weighted_price_change'].sum()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

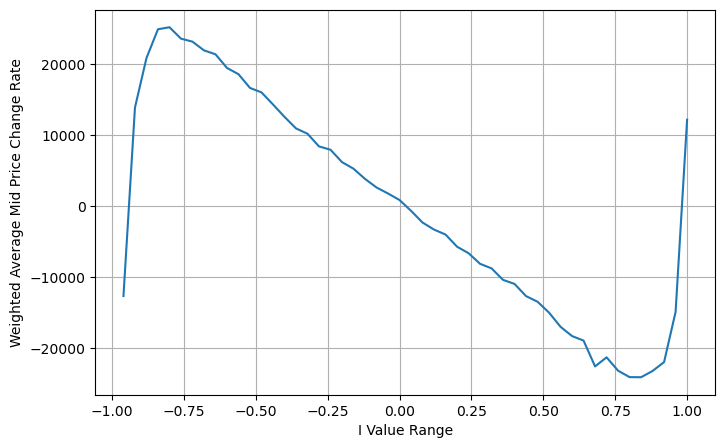
books['adjust_mid_price'] = books['mid_price'] + books['spread']*(books['I'])*(books['I']**8+1)/4
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['adjust_mid_price'] = (books['adjust_mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['adjust_mid_price'].sum()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

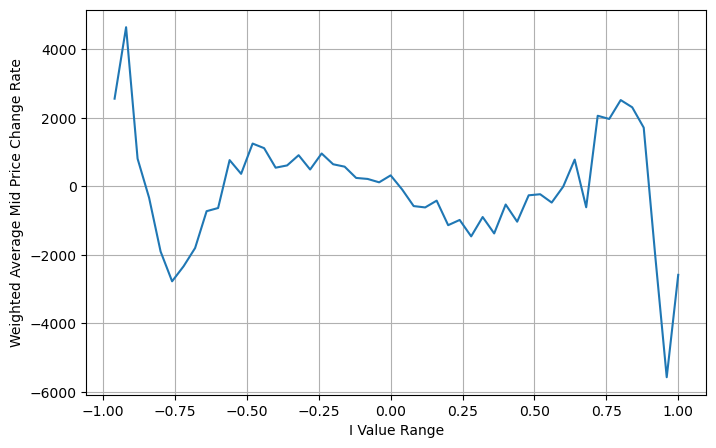
books['adjust_mid_price'] = books['mid_price'] + books['spread']*(books['I']**3)/2
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['adjust_mid_price'] = (books['adjust_mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['adjust_mid_price'].sum()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

요약하다

중간 가격은 고빈도 전략에 매우 중요합니다. 이는 미래의 단기 가격을 예측하는 것이므로 중간 가격은 가능한 한 정확해야 합니다. 위에서 소개한 중간 가격은 모두 시장 데이터를 기반으로 합니다. 분석에는 단 하나의 시장 가격만 사용되기 때문입니다. 실제 거래에서는 특히 실제 거래에서 거래소가 존재할 경우 모든 데이터를 최대한 활용하는 전략을 사용해야 하며, 중간 가격에 대한 예측은 실제 거래 가격으로 테스트해야 합니다. 저는 Stoikov가 실제 중간 가격은 매수-1매도 거래 확률의 가중 평균이어야 한다고 말하는 트윗을 게시한 것으로 기억합니다. 이 문제는 이전 기사에서 방금 연구되었습니다. 제한된 분량으로 인해 이러한 문제는 다음 기사에서 자세히 논의하겠습니다.