Pemikiran tentang strategi perdagangan frekuensi tinggi (1)
 3
3
 4856
4856

Artikel tersebut membincangkan strategi perdagangan frekuensi tinggi mata wang digital, termasuk sumber keuntungan (terutamanya daripada turun naik pasaran dan rebat yuran pertukaran), isu penempatan pesanan dan kawalan kedudukan, dan kaedah pemodelan volum dagangan menggunakan pengedaran Pareto . Di samping itu, transaksi dan data pesanan optimum yang disediakan oleh Binance telah digunakan untuk ujian balik, dan isu lain mengenai strategi perdagangan frekuensi tinggi dirancang untuk dibincangkan secara mendalam dalam artikel berikutnya.
Saya telah menulis dua artikel mengenai perdagangan frekuensi tinggi mata wang digital sebelum ini. Pengenalan terperinci kepada strategi mata wang digital frekuensi tinggi, Peroleh 80 kali dalam 5 hari, kuasa strategi frekuensi tinggi. Tetapi ia hanya boleh dianggap sebagai perkongsian pengalaman dan ceramah umum. Kali ini saya bercadang untuk menulis satu siri artikel untuk memperkenalkan idea-idea perdagangan frekuensi tinggi dari awal saya berharap untuk menjadi ringkas dan sejelas mungkin, bagaimanapun, kerana tahap saya yang terhad dan pemahaman yang mendalam tentang frekuensi tinggi perdagangan, artikel ini hanyalah titik permulaan saya harap pakar dapat membetulkan saya.
Sumber keuntungan frekuensi tinggi
Seperti yang dinyatakan dalam artikel sebelum ini, strategi frekuensi tinggi amat sesuai untuk pasaran dengan turun naik yang sangat tidak menentu. Periksa perubahan harga produk dagangan dalam tempoh masa yang singkat, yang terdiri daripada aliran keseluruhan dan turun naik. Jika kita boleh meramalkan dengan tepat perubahan dalam arah aliran, kita pasti boleh membuat wang, tetapi ini juga yang paling sukar Artikel ini terutamanya memperkenalkan strategi pembuat frekuensi tinggi dan tidak akan melibatkan isu ini. Dalam pasaran yang tidak menentu, jika strategi meletakkan pesanan ke atas dan ke bawah dilaksanakan dengan cukup kerap dan margin keuntungan cukup besar, ia boleh menampung kemungkinan kerugian yang disebabkan oleh trend, supaya anda boleh membuat keuntungan tanpa meramalkan pasaran. Pada masa ini, semua urus niaga pembuat di bursa menerima rebat pada yuran transaksi, yang juga merupakan komponen keuntungan Semakin sengit persaingan, semakin tinggi bahagian rebat yang sepatutnya.
Masalah yang perlu diselesaikan
Strategi menempatkan pesanan membeli dan menjual pesanan pada masa yang sama Soalan pertama ialah di mana untuk membuat pesanan. Semakin dekat pesanan dengan pasaran, semakin tinggi kebarangkalian urus niaga Walau bagaimanapun, dalam pasaran yang tidak menentu, harga urus niaga serta-merta mungkin jauh dari pasaran Jika pesanan diletakkan terlalu dekat, anda tidak akan dapat mendapat keuntungan yang mencukupi. Kebarangkalian pelaksanaan pesanan yang diletakkan terlalu jauh adalah rendah. Ini adalah masalah yang perlu dioptimumkan.
Kawal kedudukan anda. Untuk mengawal risiko, strategi tidak boleh mengumpul terlalu banyak kedudukan untuk masa yang lama. Ini boleh diselesaikan dengan mengawal jarak pesanan, kuantiti pesanan, jumlah had kedudukan, dsb.
Untuk mencapai matlamat di atas, adalah perlu untuk memodelkan dan menganggarkan kebarangkalian transaksi, keuntungan transaksi, anggaran pasaran dan aspek lain Terdapat banyak artikel dan kertas dalam bidang ini, yang boleh didapati dengan kata kunci seperti Perdagangan Frekuensi Tinggi. , Buku Pesanan, dsb. Terdapat banyak cadangan dalam talian, yang saya tidak akan ke sini. Di samping itu, adalah yang terbaik untuk mewujudkan sistem ujian belakang yang boleh dipercayai dan pantas Walaupun strategi frekuensi tinggi boleh disahkan dengan mudah melalui dagangan sebenar untuk mengesahkan keberkesanannya, ujian belakang masih boleh memberikan lebih banyak idea dan mengurangkan kos percubaan dan kesilapan.
Data yang diperlukan
Binance menyediakan data transaksi demi transaksi dan pesanan terbaikmuat turun,Data mendalam perlu dimuat turun menggunakan API dalam senarai putih, atau anda boleh mengumpulnya sendiri. Untuk tujuan ujian balik, anda hanya boleh menggunakan data transaksi yang dikumpul. Artikel ini mengambil data HOOKUSDT-aggTrades-2023-01-27 sebagai contoh.
from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
Lajur transaksi adalah seperti berikut:
- agg_trade_id: id pesanan transaksi agregat,
- Harga: harga transaksi
- Kuantiti: Bilangan transaksi
- first_trade_id: Mungkin terdapat beberapa transaksi dalam koleksi pada masa yang sama, hanya satu data dikira, ini adalah id transaksi pertama
- last_trade_id: id transaksi terakhir
- masa_urusniaga: masa transaksi
- is_buyer_maker: arah transaksi, True bermaksud pesanan beli didagangkan oleh pembuat, dan pesanan jual didagangkan oleh pengambil
Dapat dilihat terdapat 660,000 data transaksi pada hari tersebut, dan transaksi tersebut sangat aktif. Csv akan dilampirkan di bahagian komen.
trades = pd.read_csv('COMPUSDT-aggTrades-2023-07-02.csv')
trades
664475 rows × 7 columns
| agg_trade_id | price | quantity | first_trade_id | last_trade_id | transact_time | is_buyer_maker |
|---|---|---|---|---|---|---|
| 120719552 | 52.42 | 22.087 | 207862988 | 207862990 | 1688256004603 | False |
| 120719553 | 52.41 | 29.314 | 207862991 | 207863002 | 1688256004623 | True |
| 120719554 | 52.42 | 0.945 | 207863003 | 207863003 | 1688256004678 | False |
| 120719555 | 52.41 | 13.534 | 207863004 | 207863006 | 1688256004680 | True |
| … | … | … | … | … | … | … |
| 121384024 | 68.29 | 10.065 | 210364899 | 210364905 | 1688342399863 | False |
| 121384025 | 68.30 | 7.078 | 210364906 | 210364908 | 1688342399948 | False |
| 121384026 | 68.29 | 7.622 | 210364909 | 210364911 | 1688342399979 | True |
Pemodelan volum transaksi tunggal
Mula-mula, proses data dan bahagikan dagangan asal ke dalam kumpulan transaksi aktif pesanan beli dan kumpulan transaksi aktif pesanan jual. Selain itu, data transaksi teragregat asal ialah sekeping data pada masa yang sama, pada harga yang sama dan dalam arah yang sama Mungkin terdapat pesanan belian aktif dengan volum 100. Jika ia dibahagikan kepada berbilang transaksi dengan berbeza harga, seperti 60 dan 40, Dua keping data akan dijana, menjejaskan anggaran volum pesanan beli. Oleh itu, adalah perlu untuk mengagregatkan semula berdasarkan masa_transaksi. Selepas pengagregatan, jumlah data dikurangkan sebanyak 140,000 rekod.
trades['date'] = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index = trades['date']
buy_trades = trades[trades['is_buyer_maker']==False].copy()
sell_trades = trades[trades['is_buyer_maker']==True].copy()
buy_trades = buy_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
sell_trades = sell_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
buy_trades['interval']=buy_trades['transact_time'] - buy_trades['transact_time'].shift()
sell_trades['interval']=sell_trades['transact_time'] - sell_trades['transact_time'].shift()
print(trades.shape[0] - (buy_trades.shape[0]+sell_trades.shape[0]))
146181
Mengambil pesanan beli sebagai contoh, mula-mula lukis histogram Anda dapat melihat bahawa kesan ekor panjang adalah sangat jelas. .
buy_trades['quantity'].plot.hist(bins=200,figsize=(10, 5));
Untuk kemudahan pemerhatian, kami memotong ekor dan memerhati Kami dapat melihat bahawa semakin besar volum dagangan, semakin rendah kekerapan kejadian, dan semakin cepat trend penurunan.
buy_trades['quantity'][buy_trades['quantity']<200].plot.hist(bins=200,figsize=(10, 5));
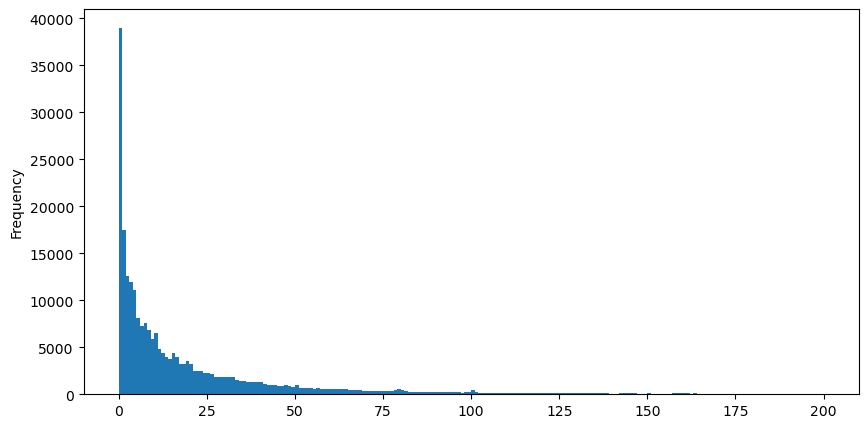
Terdapat banyak kajian mengenai taburan kepuasan volum. Pengagihan undang-undang kuasanya juga dipanggil pengedaran Pareto, yang merupakan bentuk umum pengedaran kebarangkalian dalam fizik statistik dan sains sosial. Dalam taburan undang-undang kuasa, kebarangkalian peristiwa saiz (atau kekerapan) tertentu adalah berkadar dengan beberapa eksponen negatif saiz peristiwa itu. Ciri utama bentuk pengedaran ini ialah peristiwa besar (iaitu, yang jauh dari min) berlaku lebih kerap daripada yang dijangkakan dalam banyak pengedaran lain. Ini adalah ciri pengagihan volum dagangan. Bentuk taburan Pareto ialah: P(x) = Cx^(-α). Berikut akan menunjukkan ini.
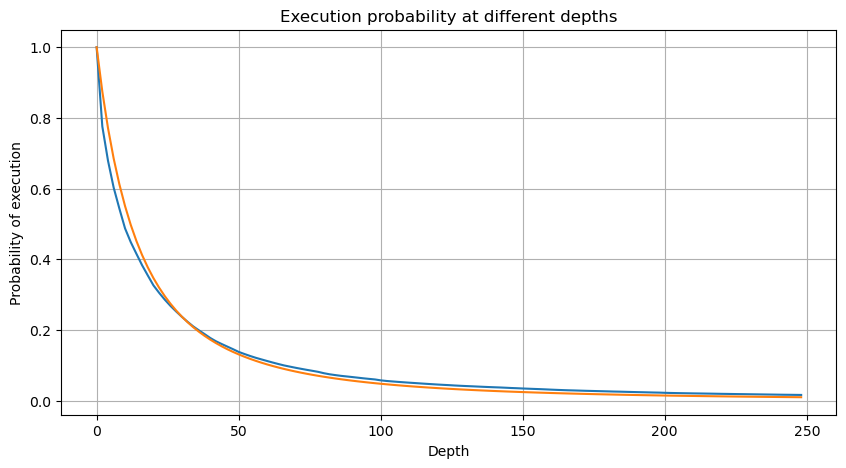
Rajah di bawah menunjukkan kebarangkalian bahawa volum dagangan lebih besar daripada nilai tertentu Garis biru ialah kebarangkalian sebenar, dan garis oren ialah kebarangkalian simulasi. Anda boleh melihat bahawa ia berlaku memenuhi pengagihan Pareto. Oleh kerana kebarangkalian bahawa volum pesanan lebih besar daripada 0 ialah 1, dan untuk memenuhi keperluan penyeragaman, persamaan taburan hendaklah seperti berikut:
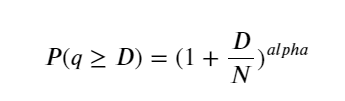
Di mana N ialah parameter piawai. Di sini kami memilih purata volum M dan alfa -2.06. Anggaran khusus alfa boleh dikira dengan mengira secara songsang nilai P apabila D=N. Khususnya: alpha = log(P(d>M))/log(2) . Memilih titik yang berbeza akan menghasilkan nilai alfa yang sedikit berbeza.
depths = range(0, 250, 2)
probabilities = np.array([np.mean(buy_trades['quantity'] > depth) for depth in depths])
alpha = np.log(np.mean(buy_trades['quantity'] > mean_quantity))/np.log(2)
mean_quantity = buy_trades['quantity'].mean()
probabilities_s = np.array([(1+depth/mean_quantity)**alpha for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)
plt.figure(figsize=(10, 5))
plt.grid(True)
plt.title('Diff')
plt.plot(depths, probabilities_s-probabilities);
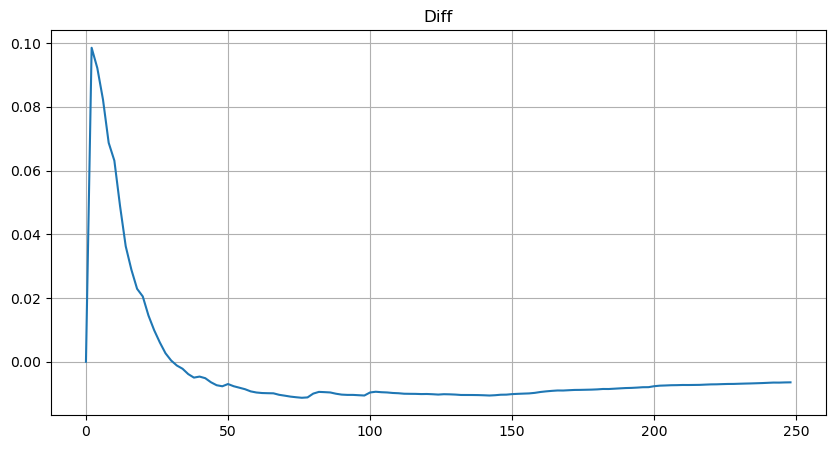
Tetapi anggaran ini hanya kelihatan seperti itu Dalam rajah di atas, kami memplot perbezaan antara nilai simulasi dan nilai sebenar. Apabila jumlah dagangan kecil, sisihan adalah besar, malah hampir 10%. Kebarangkalian titik boleh dibuat lebih tepat dengan memilih titik yang berbeza semasa anggaran parameter, tetapi ini tidak menyelesaikan masalah sisihan. Ini ditentukan oleh perbezaan antara pengagihan undang-undang kuasa dan pengagihan sebenar Untuk mendapatkan keputusan yang lebih tepat, persamaan pengagihan undang-undang kuasa perlu diperbetulkan. Saya tidak akan menerangkan secara terperinci tentang proses tertentu, tetapi saya mendapat inspirasi dan mendapati ia sepatutnya seperti berikut:
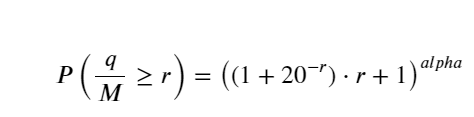
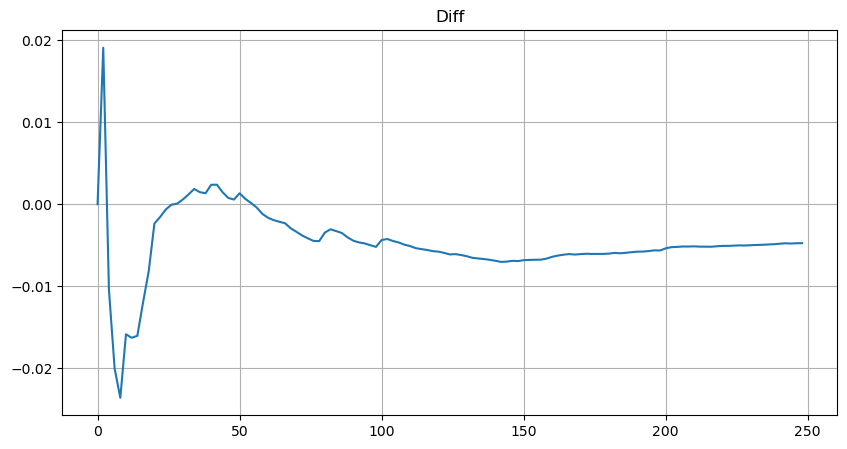
Untuk kesederhanaan, r = q/M digunakan di sini untuk mewakili volum dagangan piawai. Parameter boleh dianggarkan dengan cara yang sama seperti di atas. Rajah di bawah menunjukkan bahawa sisihan maksimum selepas pembetulan tidak melebihi 2%.
depths = range(0, 250, 2)
probabilities = np.array([np.mean(buy_trades['quantity'] > depth) for depth in depths])
mean = buy_trades['quantity'].mean()
alpha = np.log(np.mean(buy_trades['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([(((1+20**(-depth/mean))*depth+mean)/mean)**alpha for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)
plt.figure(figsize=(10, 5))
plt.grid(True)
plt.title('Diff')
plt.plot(depths, probabilities_s-probabilities);
Dengan persamaan anggaran untuk taburan isipadu, ambil perhatian bahawa kebarangkalian persamaan itu bukanlah kebarangkalian sebenar, tetapi kebarangkalian bersyarat. Pada ketika ini kita boleh menjawab soalan ini: jika tertib seterusnya berlaku, apakah kebarangkalian pesanan ini lebih besar daripada nilai tertentu? Dalam erti kata lain, apakah kebarangkalian pelaksanaan pesanan dengan kedalaman yang berbeza (keadaan ideal, tidak begitu ketat, secara teori buku pesanan mempunyai pesanan baru dan pembatalan, serta baris gilir pada kedalaman yang sama).
Artikel itu hampir selesai di sini, dan masih banyak soalan yang perlu dijawab.