Você pode ultrapassar gorilas apostando (negociando) com máquinas de vetores SVM?

Senhoras e senhores, façam as vossas apostas. Hoje, vamos fazer o nosso melhor para derrotar um orangotango, considerado um dos adversários mais terríveis do mundo financeiro. Vamos tentar prever o lucro de um dia para o outro de uma variedade de negociação monetária. Garanto-lhe que é muito difícil vencer um macaco que faz uma aposta aleatória e tem uma probabilidade de 50% de vencer. Vamos usar um algoritmo de aprendizagem de máquina já existente, que suporta classificadores vetoriais. A máquina vetorial SVM é uma maneira incrivelmente poderosa de resolver tarefas de regressão e classificação.

• SVM compatível com vectores

A máquina vetorial SVM é baseada na idéia de que podemos classificar o espaço de características p para o superplano. O algoritmo da máquina vetorial SVM usa um superplano e uma Margem de Identificação para criar a fronteira de decisão de classificação, como mostrado abaixo.

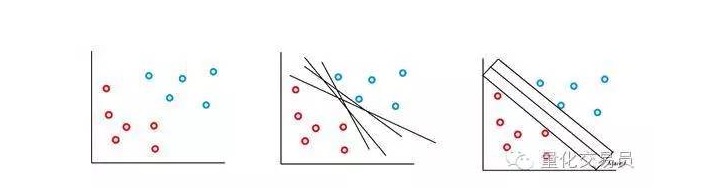
No caso mais simples, a classificação linear é possível. O algoritmo escolhe a fronteira de decisão, que pode maximizar a distância entre as classes.

Na maioria das sequências de tempo financeiras que você enfrenta, é pouco provável que você encontre conjuntos simples e linearmente separáveis, mas os indivisíveis são frequentes. A máquina vetorial SVM resolve esse problema através da implementação de um método conhecido como método de margem suave.

Neste caso, alguns casos de classificação errônea são permitidos, mas eles executam a função por si mesmos, de modo a reduzir o fator e a distância entre o erro e a borda de forma proporcional a C (errores de custo ou orçamento podem ser permitidos).

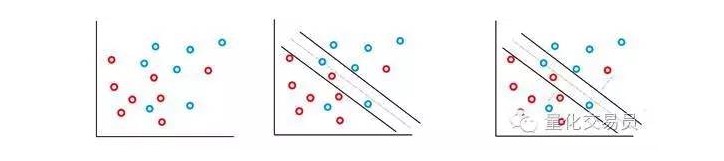
Basicamente, a máquina maximiza o intervalo entre as categorizações, enquanto minimiza os seus elementos de penalização ponderados por C.

O classificador SVM possui uma excelente característica de que a localização e o tamanho da fronteira de decisão de classificação são determinados apenas por parte dos dados, ou seja, os dados mais próximos da fronteira de decisão. Esta característica do algoritmo permite que ele possa combater a interferência de valores anormais de distância.

Bem, eu acho que a diversão está apenas começando.

Considere o seguinte ((separar pontos vermelhos de outras cores):

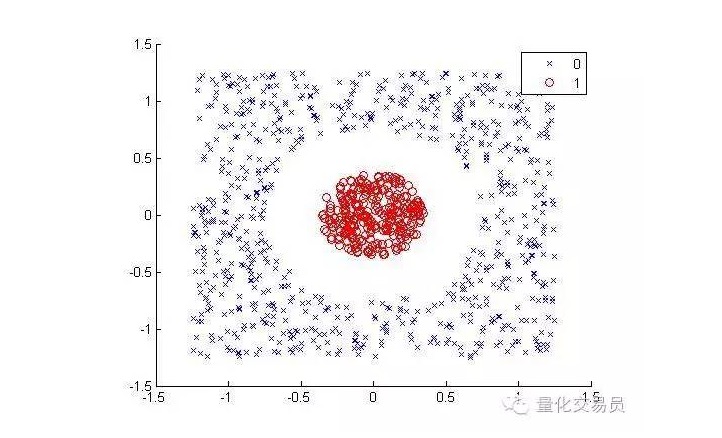
Para os seres humanos, a classificação é muito simples (uma linha ovalada pode ser) mas não é o mesmo para as máquinas. É óbvio que não pode ser feito em linha reta (uma linha reta não pode separar os pontos vermelhos). Aqui podemos tentar o truque do núcleo de silicone (o truque do kernel).

A técnica do núcleo interno é uma técnica matemática muito inteligente que nos permite resolver classificações lineares em espaços de alta dimensão. Agora vamos ver como isso é feito.

Vamos transformar o espaço de características bidimensionais em tridimensionais por meio de mapeamento por elevação, voltando para a segunda dimensão depois de concluída a classificação.

A seguir, imagens de mapeamento em escala e classificação:

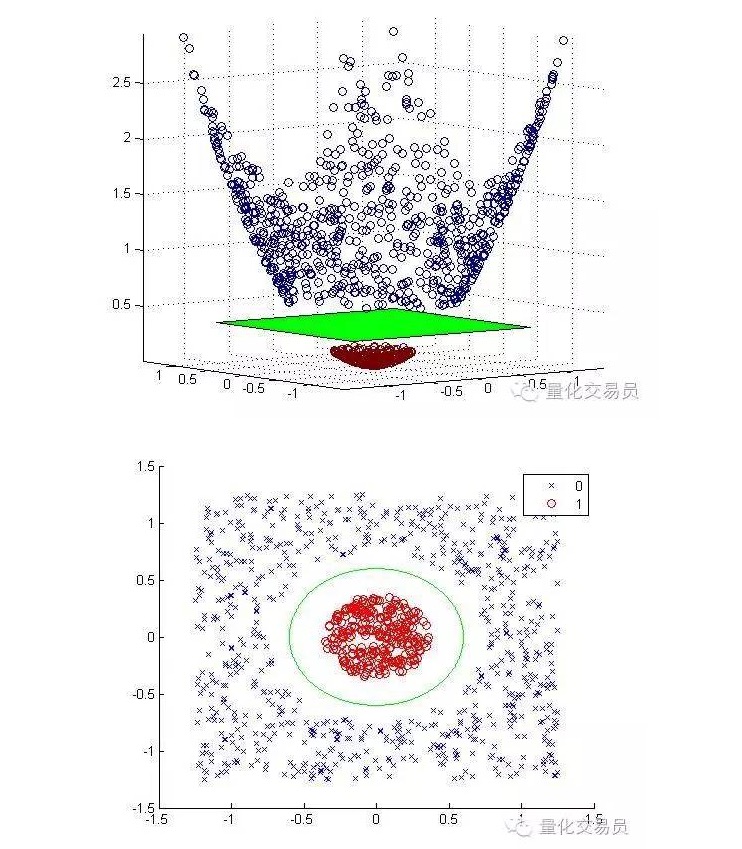
Em geral, se houver d entradas, você pode usar um mapeamento do espaço de entrada d-dimensional para o espaço de característica p-dimensional. Execute a solução que o algoritmo de minimização acima produzirá e mapeie de volta ao seu espaço de entrada original para o superplano p-dimensional.

A premissa importante para a solução matemática acima, depende de como gerar um bom conjunto de amostras de pontos no espaço de características.

Você só precisa de um conjunto de amostras de pontos para executar a optimização de fronteiras, o mapeamento não precisa ser definido, e os pontos do espaço de entrada em um espaço de características de alta dimensão podem ser calculados com segurança por meio da função nuclear ((e um pouco da ajuda do teorema de Mercer)).

Por exemplo, se você quiser resolver seu problema de classificação em um espaço de características gigantesco, suponha que seja de 100000 dimensões. Você pode imaginar a capacidade de computação que você precisaria? Eu duvido muito que você consiga fazer isso.

• Desafios e gorilas

Agora estamos nos preparando para enfrentar o desafio de derrotar a capacidade de previsão de Jeff.

Jeff é um especialista em mercados monetários, e ele conseguiu uma precisão de 50% de previsão através de uma aposta aleatória, que é um sinal de previsão da taxa de retorno do dia seguinte.

Vamos usar diferentes sequências de tempo básicas, incluindo a sequência de preços em tempo real, cada sequência de tempo com ganhos de até 10 lags, para um total de 55 características.

A máquina vetorial SVM que estamos construindo usa o núcleo de 3 graus. Como você pode imaginar, escolher um núcleo adequado é outra tarefa muito difícil. Para calibrar os parâmetros C e Γ, a verificação de cruzamento triplo é executada em uma grelha de possíveis combinações de parâmetros, e o melhor conjunto será selecionado.

Os resultados não são muito animadores:

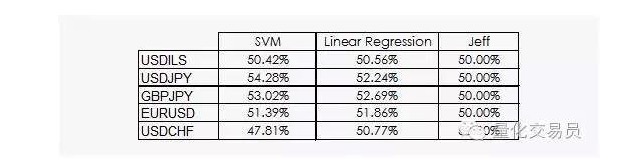
Podemos ver que tanto a regressão linear quanto a máquina vetorial SVM são capazes de derrotar o Jeff. Embora os resultados não sejam otimistas, também podemos extrair alguma informação dos dados, o que já é uma boa notícia, porque na disciplina de dados, o ganho diário da sequência de tempo financeira não é o mais útil.

Após a verificação cruzada, o conjunto de dados será treinado e testado, e nós registramos a capacidade de previsão do SVM treinado, repetindo a divisão aleatória de cada moeda 1000 vezes para ter um desempenho estável.

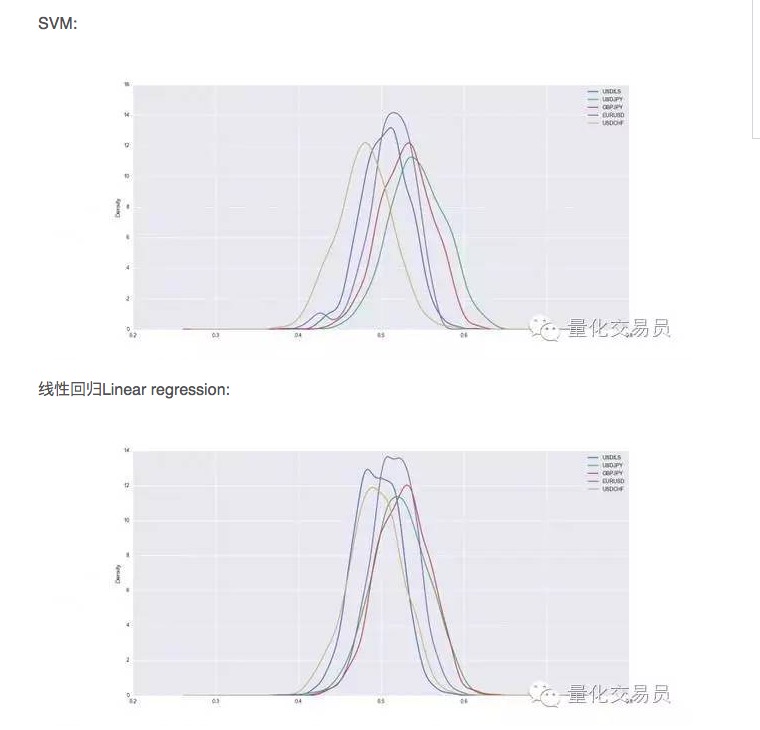
Assim, em alguns casos, o SVM é melhor do que a simples regressão linear, mas o desempenho também é um pouco maior. No caso do dólar versus o iene, por exemplo, o sinal que podemos prever em média é 54% do total. É um resultado bastante bom, mas vamos ver mais de perto!

Ted é o primo de Jeff, que também é um gorila, mas é mais inteligente do que ele. Ted olha para o conjunto de amostras de treinamento, não para apostas aleatórias.

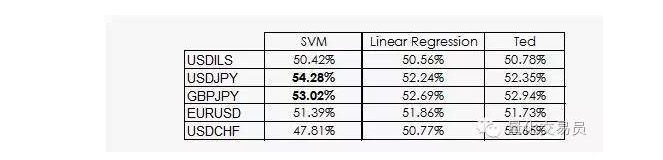
Como vimos, o desempenho da maioria dos SVMs vem apenas de um fato: a aprendizagem da máquina mostra que a classificação é improvável de ser igual à antecedência. Na verdade, a regressão linear não pode obter qualquer informação do espaço de características, mas a interseção (intercept) na regressão faz sentido, e a interseção e a coluna de uma classificação são mais eficientes.

Uma notícia um pouco melhor é que a máquina vetorial SVM consegue obter algumas informações não-lineares adicionais a partir dos dados, o que nos permite sugerir uma precisão de 2% nas previsões.

Infelizmente, ainda não sabemos que tipo de informação pode ser, assim como a máquina vetorial SVM tem suas próprias principais desvantagens, que não podemos explicar claramente.

Autor: P. López, publicado em quantdare Transcrição feita pelo WeChat Public