Reflexões sobre estratégias de negociação de alta frequência (2)
 1
1
 3416
3416
O artigo discute principalmente estratégias de negociação de alta frequência, com foco em modelagem de volume cumulativo e choques de preços. Este artigo propõe um modelo preliminar de colocação ótima de ordens analisando o impacto de transações únicas, choques de preços em intervalos fixos e volume de transações nos preços. Este modelo tenta encontrar a posição de negociação ideal com base na compreensão dos choques de volume e preço. As premissas do modelo são discutidas em profundidade, e uma avaliação preliminar da colocação ideal da ordem é feita comparando os retornos esperados reais e previstos pelo modelo.
Modelagem de Volume Cumulativo
O artigo anterior derivou a expressão de probabilidade para um único volume de transação ser maior que um determinado valor:
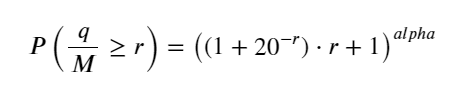
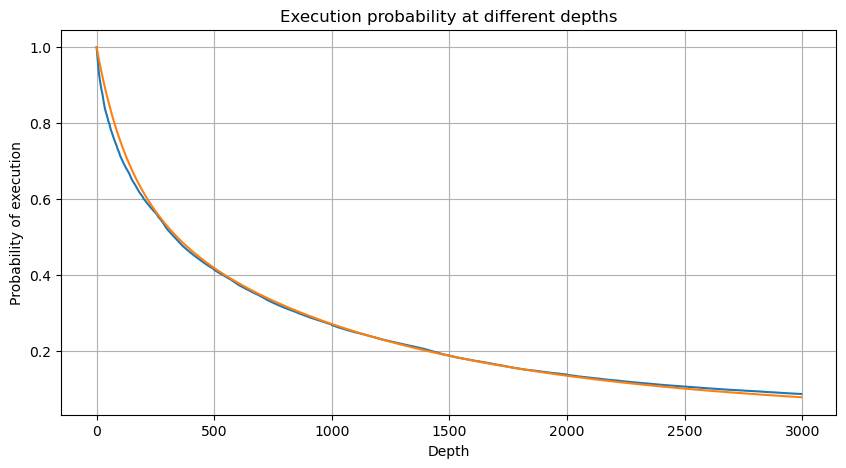
Também estamos preocupados com a distribuição do volume de negociação ao longo de um período de tempo, que intuitivamente deve estar relacionado ao volume de cada transação e à frequência das ordens. Em seguida, os dados são processados em intervalos fixos. Trace sua distribuição como acima.
from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
trades = pd.read_csv('HOOKUSDT-aggTrades-2023-01-27.csv')
trades['date'] = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index = trades['date']
buy_trades = trades[trades['is_buyer_maker']==False].copy()
buy_trades = buy_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
buy_trades['interval']=buy_trades['transact_time'] - buy_trades['transact_time'].shift()
buy_trades.index = buy_trades['date']
Mescle o volume de transações a cada 1s, remova a parte onde nenhuma transação ocorreu e use a distribuição de transação única acima para ajustar. Pode-se ver que o resultado é melhor. Se todas as transações dentro de 1s forem consideradas transações únicas, esse problema se torna Tornou-se um problema resolvido. Entretanto, quando o ciclo é prolongado (em relação à frequência da transação), o erro aumenta, e pesquisas descobriram que esse erro é causado pelo termo de correção anterior da distribuição de Pareto. Isso significa que, à medida que o ciclo se alonga e inclui mais transações individuais, a combinação de múltiplas transações se aproxima da distribuição de Pareto. Nesse caso, o termo de correção deve ser removido.
df_resampled = buy_trades['quantity'].resample('1S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
buy_trades
| agg_trade_id | price | quantity | first_trade_id | last_trade_id | is_buyer_maker | date | transact_time | interval | diff | |
|---|---|---|---|---|---|---|---|---|---|---|
| 2023-01-27 00:00:00.161 | 1138369 | 2.901 | 54.3 | 3806199 | 3806201 | False | 2023-01-27 00:00:00.161 | 1674777600161 | NaN | 0.001 |
| 2023-01-27 00:00:04.140 | 1138370 | 2.901 | 291.3 | 3806202 | 3806203 | False | 2023-01-27 00:00:04.140 | 1674777604140 | 3979.0 | 0.000 |
| 2023-01-27 00:00:04.339 | 1138373 | 2.902 | 55.1 | 3806205 | 3806207 | False | 2023-01-27 00:00:04.339 | 1674777604339 | 199.0 | 0.001 |
| 2023-01-27 00:00:04.772 | 1138374 | 2.902 | 1032.7 | 3806208 | 3806223 | False | 2023-01-27 00:00:04.772 | 1674777604772 | 433.0 | 0.000 |
| 2023-01-27 00:00:05.562 | 1138375 | 2.901 | 3.5 | 3806224 | 3806224 | False | 2023-01-27 00:00:05.562 | 1674777605562 | 790.0 | 0.000 |
| … | … | … | … | … | … | … | … | … | … | … |
| 2023-01-27 23:59:57.739 | 1544370 | 3.572 | 394.8 | 5074645 | 5074651 | False | 2023-01-27 23:59:57.739 | 1674863997739 | 1224.0 | 0.002 |
| 2023-01-27 23:59:57.902 | 1544372 | 3.573 | 177.6 | 5074652 | 5074655 | False | 2023-01-27 23:59:57.902 | 1674863997902 | 163.0 | 0.001 |
| 2023-01-27 23:59:58.107 | 1544373 | 3.573 | 139.8 | 5074656 | 5074656 | False | 2023-01-27 23:59:58.107 | 1674863998107 | 205.0 | 0.000 |
| 2023-01-27 23:59:58.302 | 1544374 | 3.573 | 60.5 | 5074657 | 5074657 | False | 2023-01-27 23:59:58.302 | 1674863998302 | 195.0 | 0.000 |
| 2023-01-27 23:59:59.894 | 1544376 | 3.571 | 12.1 | 5074662 | 5074664 | False | 2023-01-27 23:59:59.894 | 1674863999894 | 1592.0 | 0.000 |
#1s内的累计分布
depths = np.array(range(0, 3000, 5))
probabilities = np.array([np.mean(df_resampled['quantity'] > depth) for depth in depths])
mean = df_resampled['quantity'].mean()
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([((1+20**(-depth/mean))*depth/mean+1)**(alpha) for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)
df_resampled = buy_trades['quantity'].resample('30S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
depths = np.array(range(0, 12000, 20))
probabilities = np.array([np.mean(df_resampled['quantity'] > depth) for depth in depths])
mean = df_resampled['quantity'].mean()
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([((1+20**(-depth/mean))*depth/mean+1)**(alpha) for depth in depths])
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2)
probabilities_s_2 = np.array([(depth/mean+1)**alpha for depth in depths]) # 无修正
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities,label='Probabilities (True)')
plt.plot(depths, probabilities_s, label='Probabilities (Simulation 1)')
plt.plot(depths, probabilities_s_2, label='Probabilities (Simulation 2)')
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.legend()
plt.grid(True)
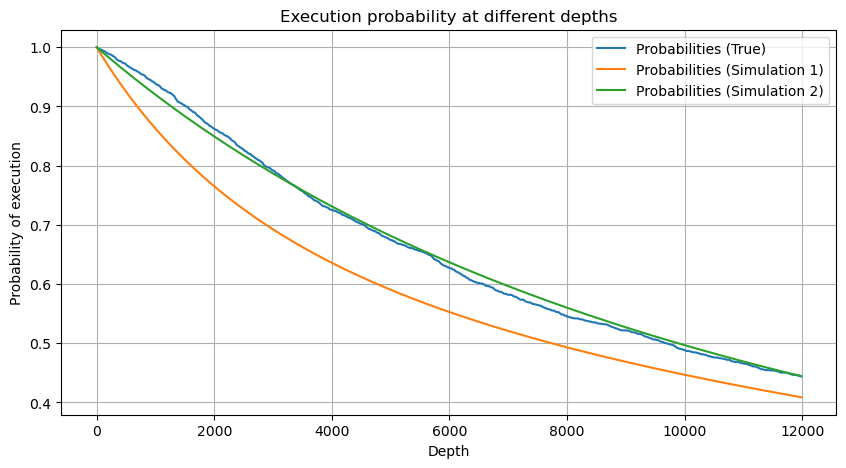
Agora, resumimos uma fórmula geral para a distribuição do volume de negociação acumulado em diferentes momentos e usamos a distribuição de transações individuais para ajustá-la, sem precisar contá-las separadamente a cada vez. Aqui omitimos o processo e damos a fórmula diretamente:
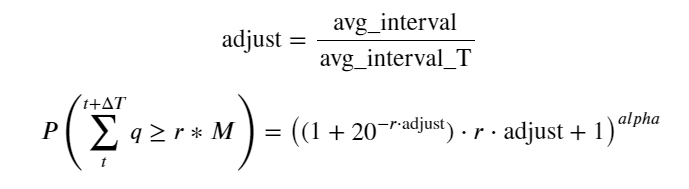
Entre eles, avg_interval representa o intervalo médio entre transações únicas, e avg_interval_T representa o intervalo médio dos intervalos que precisam ser estimados. É um pouco confuso. Se quisermos estimar o tempo de transação de 1 segundo, precisamos calcular o intervalo médio entre eventos que contêm transações dentro de 1 segundo. Se a probabilidade de um pedido chegar estiver de acordo com a distribuição de Poisson, deve ser possível estimá-la diretamente aqui, mas o desvio real é grande, então não o explicarei aqui.
Note que a probabilidade do volume ser maior que um determinado valor dentro de um determinado intervalo deve ser bem diferente da probabilidade real da transação naquela posição na profundidade, pois quanto maior o tempo de espera, maior a possibilidade do livro de ordens mudando, e a transação também leva a As mudanças de profundidade, então a probabilidade de transação na mesma posição de profundidade muda em tempo real conforme os dados são atualizados.
df_resampled = buy_trades['quantity'].resample('2S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
depths = np.array(range(0, 6500, 10))
probabilities = np.array([np.mean(df_resampled['quantity'] > depth) for depth in depths])
mean = buy_trades['quantity'].mean()
adjust = buy_trades['interval'].mean() / 2620
alpha = np.log(np.mean(buy_trades['quantity'] > mean))/0.7178397931503168
probabilities_s = np.array([((1+20**(-depth*adjust/mean))*depth*adjust/mean+1)**(alpha) for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)
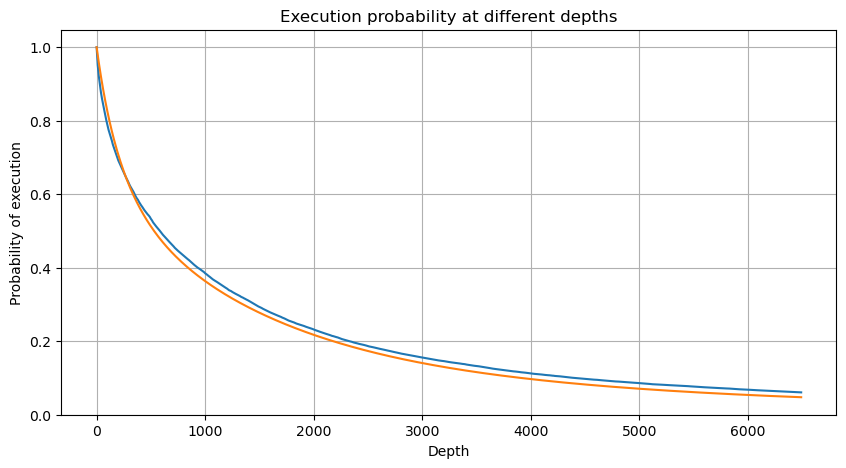
Impacto no preço de uma única transação
Dados de transações são um tesouro, e ainda há muitos dados a serem explorados. Devemos prestar muita atenção ao impacto das ordens nos preços, o que afeta a colocação de ordens pendentes na estratégia. Similarmente, com base nos dados agregados transact_time, calcule a diferença entre o último preço e o primeiro preço. Se houver apenas um pedido, a diferença é 0. O estranho é que ainda há um pequeno número de resultados de dados com resultados negativos. Isso deve ser um problema com a ordem de arranjo dos dados, então não vou entrar nisso aqui.
Os resultados mostram que a proporção de nenhum impacto é tão alta quanto 77%, a proporção de 1 carrapato é de 16,5%, 2 carrapatos é de 3,7%, 3 carrapatos é de 1,2% e a proporção de mais de 4 carrapatos é inferior a 1%. . Isso basicamente está de acordo com as características da função exponencial, mas o ajuste não é preciso.
O volume de transação que causou a diferença de preço correspondente foi contado, e a distorção causada por um impacto muito grande foi removida. Ele basicamente se conforma com a relação linear, e cerca de cada 1.000 volumes causa uma flutuação de preço de 1 tick. Também pode ser entendido que o número médio de ordens pendentes perto de cada preço é de cerca de 1.000.
diff_df = trades[trades['is_buyer_maker']==False].groupby('transact_time')['price'].agg(lambda x: abs(round(x.iloc[-1] - x.iloc[0],3)) if len(x) > 1 else 0)
buy_trades['diff'] = buy_trades['transact_time'].map(diff_df)
diff_counts = buy_trades['diff'].value_counts()
diff_counts[diff_counts>10]/diff_counts.sum()
0.000 0.769965
0.001 0.165527
0.002 0.037826
0.003 0.012546
0.004 0.005986
0.005 0.003173
0.006 0.001964
0.007 0.001036
0.008 0.000795
0.009 0.000474
0.010 0.000227
0.011 0.000187
0.012 0.000087
0.013 0.000080
Name: diff, dtype: float64
diff_group = buy_trades.groupby('diff').agg({
'quantity': 'mean',
'diff': 'last',
})
diff_group['quantity'][diff_group['diff']>0][diff_group['diff']<0.01].plot(figsize=(10,5),grid=True);
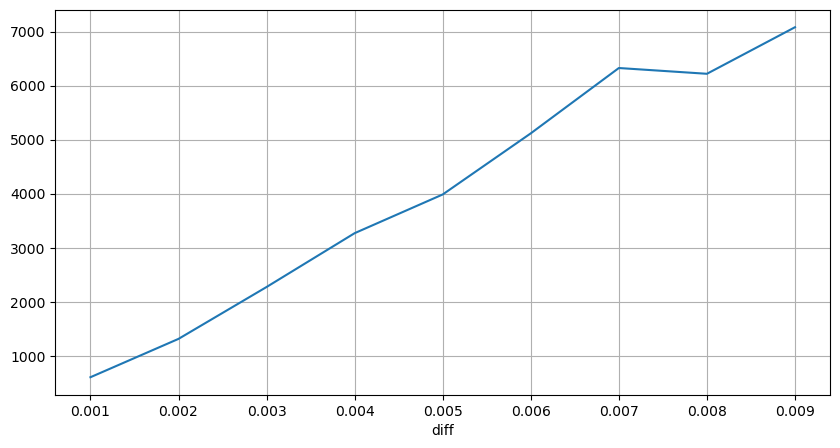
Choques de preços em intervalos regulares
Conte o impacto do preço em 2 segundos. A diferença aqui é que haverá valores negativos. Claro, como apenas ordens de compra são contadas aqui, a posição simétrica será um tick maior. Continue observando a relação entre volume de negociação e impacto, e conte apenas os resultados maiores que 0. A conclusão é semelhante à de uma única ordem, que também é uma relação linear aproximada. Cada tick requer aproximadamente 2000 volumes.
df_resampled = buy_trades.resample('2S').agg({
'price': ['first', 'last', 'count'],
'quantity': 'sum'
})
df_resampled['price_diff'] = round(df_resampled[('price', 'last')] - df_resampled[('price', 'first')],3)
df_resampled['price_diff'] = df_resampled['price_diff'].fillna(0)
result_df_raw = pd.DataFrame({
'price_diff': df_resampled['price_diff'],
'quantity_sum': df_resampled[('quantity', 'sum')],
'data_count': df_resampled[('price', 'count')]
})
result_df = result_df_raw[result_df_raw['price_diff'] != 0]
result_df['price_diff'][abs(result_df['price_diff'])<0.016].value_counts().sort_index().plot.bar(figsize=(10,5));
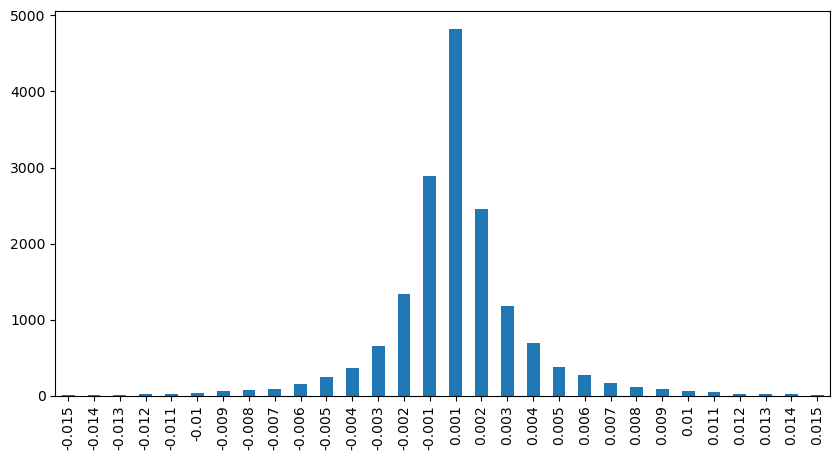
result_df['price_diff'].value_counts()[result_df['price_diff'].value_counts()>30]
0.001 7176
-0.001 3665
0.002 3069
-0.002 1536
0.003 1260
0.004 692
-0.003 608
0.005 391
-0.004 322
0.006 259
-0.005 192
0.007 146
-0.006 112
0.008 82
0.009 75
-0.007 75
-0.008 65
0.010 51
0.011 41
-0.010 31
Name: price_diff, dtype: int64
diff_group = result_df.groupby('price_diff').agg({ 'quantity_sum': 'mean'})
diff_group[(diff_group.index>0) & (diff_group.index<0.015)].plot(figsize=(10,5),grid=True);
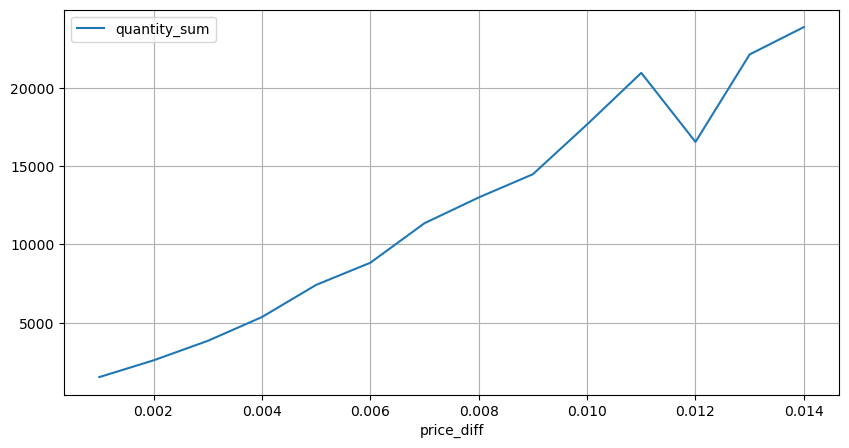
Impacto do volume no preço
O volume necessário para uma mudança de tick foi calculado anteriormente, mas não é preciso porque se baseia na suposição de que o impacto já ocorreu. Agora vamos analisar o impacto do preço causado pelo volume de negociação.
Os dados aqui são amostrados em 1 segundo, com 100 quantidades em 1 etapa, e as alterações de preço dentro desse intervalo de quantidade são contadas. Algumas conclusões valiosas foram tiradas:
- Quando o volume de compra está abaixo de 500, a mudança de preço esperada é para baixo, o que é esperado, pois também há ordens de venda afetando o preço.
- Quando o volume de negociação é baixo, ele segue uma relação linear, ou seja, quanto maior o volume de negociação, maior o aumento de preço.
- Quanto maior o volume da ordem de compra, maior a mudança de preço, o que frequentemente representa um rompimento de preço. Após o rompimento, o preço pode retornar. Juntamente com a amostragem em intervalos fixos, os dados são instáveis.
- Deve-se prestar atenção à parte superior do gráfico de dispersão, ou seja, a parte onde o volume corresponde ao aumento do preço.
- Somente para este par de negociação, é fornecida uma versão aproximada da relação entre volume e mudança de preço:
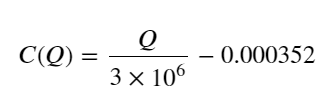
Entre eles, “C” representa a mudança no preço e “Q” representa o volume da ordem de compra.
df_resampled = buy_trades.resample('1S').agg({
'price': ['first', 'last', 'count'],
'quantity': 'sum'
})
df_resampled['price_diff'] = round(df_resampled[('price', 'last')] - df_resampled[('price', 'first')],3)
df_resampled['price_diff'] = df_resampled['price_diff'].fillna(0)
result_df_raw = pd.DataFrame({
'price_diff': df_resampled['price_diff'],
'quantity_sum': df_resampled[('quantity', 'sum')],
'data_count': df_resampled[('price', 'count')]
})
result_df = result_df_raw[result_df_raw['price_diff'] != 0]
df = result_df.copy()
bins = np.arange(0, 30000, 100) #
labels = [f'{i}-{i+100-1}' for i in bins[:-1]]
df.loc[:, 'quantity_group'] = pd.cut(df['quantity_sum'], bins=bins, labels=labels)
grouped = df.groupby('quantity_group')['price_diff'].mean()
grouped_df = pd.DataFrame(grouped).reset_index()
grouped_df['quantity_group_center'] = grouped_df['quantity_group'].apply(lambda x: (float(x.split('-')[0]) + float(x.split('-')[1])) / 2)
plt.figure(figsize=(10,5))
plt.scatter(grouped_df['quantity_group_center'], grouped_df['price_diff'],s=10)
plt.plot(grouped_df['quantity_group_center'], np.array(grouped_df['quantity_group_center'].values)/2e6-0.000352,color='red')
plt.xlabel('quantity_group_center')
plt.ylabel('average price_diff')
plt.title('Scatter plot of average price_diff by quantity_group')
plt.grid(True)
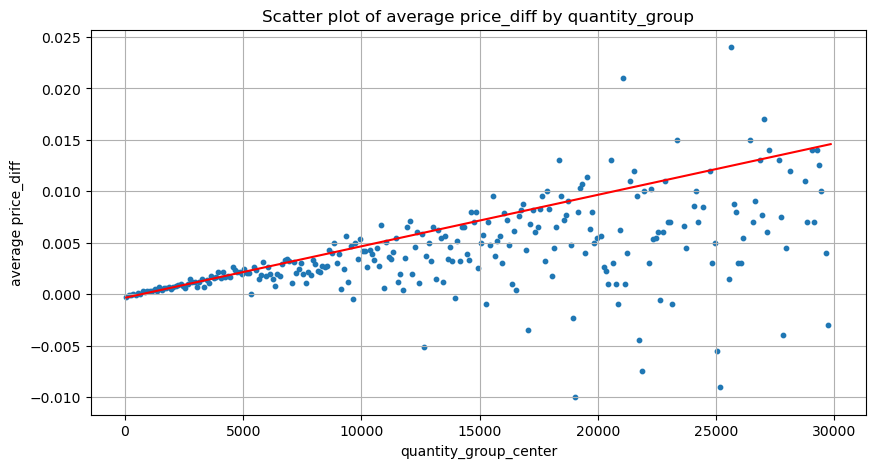
grouped_df.head(10)
| quantity_group | price_diff | quantity_group_center | |
|---|---|---|---|
| 0 | 0-199 | -0.000302 | 99.5 |
| 1 | 100-299 | -0.000124 | 199.5 |
| 2 | 200-399 | -0.000068 | 299.5 |
| 3 | 300-499 | -0.000017 | 399.5 |
| 4 | 400-599 | -0.000048 | 499.5 |
| 5 | 500-699 | 0.000098 | 599.5 |
| 6 | 600-799 | 0.000006 | 699.5 |
| 7 | 700-899 | 0.000261 | 799.5 |
| 8 | 800-999 | 0.000186 | 899.5 |
| 9 | 900-1099 | 0.000299 | 999.5 |
Posição inicial ótima da ordem
Com a modelagem do volume de negociação e um modelo aproximado do volume de negociação correspondente ao impacto do preço, parece que a posição ideal da ordem pode ser calculada. Vamos fazer algumas suposições e dar uma posição de preço ótima irresponsável.
- Suponha que o preço retorne ao seu valor original após o choque (isso é obviamente improvável e requer uma reanálise das mudanças de preço após o choque)
- Suponha que a distribuição do volume de negociação e da frequência de ordens durante esse período atenda aos requisitos predefinidos (isso também é impreciso, pois o valor de um dia é usado para estimativa, e as transações têm agrupamento óbvio).
- Suponha que apenas uma ordem de venda ocorra durante o tempo de simulação e então a posição seja fechada.
- Supondo que após a ordem ser executada, existam outras ordens de compra para continuar a empurrar o preço para cima, especialmente quando o volume está muito baixo. Este efeito é ignorado aqui e é simplesmente assumido que ele retornará.
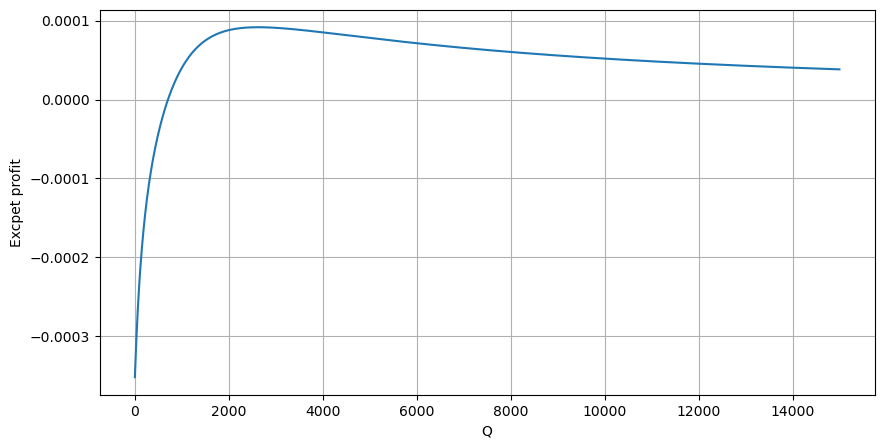
Primeiro, escreva um retorno esperado simples, ou seja, a probabilidade de que a ordem de compra cumulativa seja maior que Q em 1 segundo, multiplicada pela taxa de retorno esperada (ou seja, o preço de impacto):
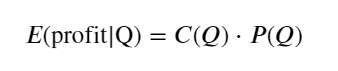
De acordo com o gráfico, o retorno esperado é máximo em torno de 2.500, o que é cerca de 2,5 vezes o volume médio de negociação. Ou seja, a ordem de venda deve ser colocada em 2500. É preciso enfatizar novamente que o eixo horizontal representa o volume de negociação em 1 segundo e não pode ser simplesmente equiparado à posição de profundidade. E isso acontece em um momento em que ainda faltam dados muito importantes e aprofundados, e eles são baseados apenas em especulações baseadas em negociações.
Resumir
Verifica-se que a distribuição de volume em diferentes intervalos de tempo é uma escala simples da distribuição de volume de uma única transação. Também fizemos um modelo simples de retorno esperado com base em choques de preço e probabilidade de transação. Os resultados deste modelo estão em linha com nossas expectativas. Se o volume da ordem de venda for pequeno, isso indica uma queda de preço. Uma certa quantidade de volume é necessária para têm margens de lucro, e quanto maior o volume de transações, maior a margem de lucro. Quanto maior a probabilidade, menor ela é. Há um tamanho ótimo no meio, que também é a posição de colocação de ordem que a estratégia está buscando. Claro, esse modelo ainda é muito simples. No próximo artigo, continuarei a discuti-lo em profundidade.
#1s内的累计分布
df_resampled = buy_trades['quantity'].resample('1S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
depths = np.array(range(0, 15000, 10))
mean = df_resampled['quantity'].mean()
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([((1+20**(-depth/mean))*depth/mean+1)**(alpha) for depth in depths])
profit_s = np.array([depth/2e6-0.000352 for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities_s*profit_s)
plt.xlabel('Q')
plt.ylabel('Excpet profit')
plt.grid(True)