Можно ли обогнать горилл, делая ставки (торгуя) с помощью векторных машин SVM?

Дамы и господа, поставьте ваши ставки. Сегодня мы сделаем все возможное, чтобы победить оранжевого обезьяну, который считается одним из самых страшных противников в финансовом мире. Мы попробуем предсказать следующий день прибыли в валютных биржах. Уверяю вас, даже если вы хотите победить случайную ставку с 50% вероятностью выигрыша, это будет очень сложно. Мы будем использовать готовый алгоритм машинного обучения, который поддерживает векторный классификатор.

• SVM поддерживает векторные машины

SVM-векторная машина основана на идее, что мы можем использовать суперпланы для классификации p-образных пространств. Алгоритм SVM-векторной машины использует суперпланы и идентификационную маржу для создания границ классификационных решений, как показано ниже.

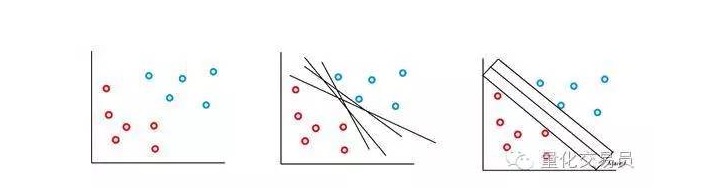
В простейшем случае возможна линейная классификация. Алгоритм выбирает границу решения, которая позволяет максимизировать расстояние между классами.

В большинстве финансовых временных рядов, с которыми вы столкнетесь, вы вряд ли столкнетесь с простой, линейно разделяемой совокупностью, а неразделимые случаи встречаются довольно часто. Векторная машина SVM решает эту проблему, применяя метод, известный как метод мягкой маржи.

В данном случае допускаются некоторые ошибочные классификации, но они сами выполняют функцию, чтобы свести к минимуму коэффициент и расстояние от ошибки до границы, пропорциональные C (считается, что ошибка в стоимости или бюджете может быть допущена).

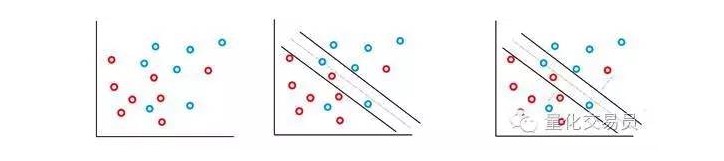
По сути, машина будет максимально увеличивать промежутки между классификациями, но при этом будет максимально уменьшать штрафные пункты, на которые накладывает вес C.

У классификатора SVM есть замечательная особенность - расположение и размер границы классификационного решения определяются только частью данных, то есть той частью данных, которая ближе к границе решения. Эта особенность алгоритма позволяет ему противостоять помехам от экстраординарных значений, которые находятся далеко друг от друга. Например, синяя точка в правом верхнем углу имеет небольшое влияние на границу решения.

Я не думаю, что это слишком сложно, но я думаю, что это только начало.

Рассмотрите следующие обстоятельства ((отделите красную точку от точек других цветов):

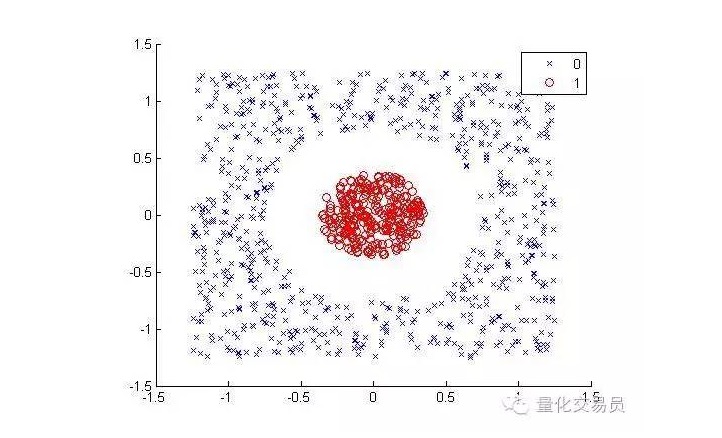
Для человека это классификация очень проста (оболочка, конечно). Но для машины это не так. Очевидно, что она не может быть сделана прямой (прямая линия не может отделить красную точку).

Внутриядерная техника - это очень умная математическая техника, которая позволяет нам решать линейные классификационные задачи в высокомерном пространстве. Давайте посмотрим, как это делается.

Мы будем переводить двумерное пространство характеристик в трехмерное с помощью масштабирования, а после классификации вернемся обратно в два измерения.

Ниже приведены картинки, выполненные с помощью масштабирования и классификации:

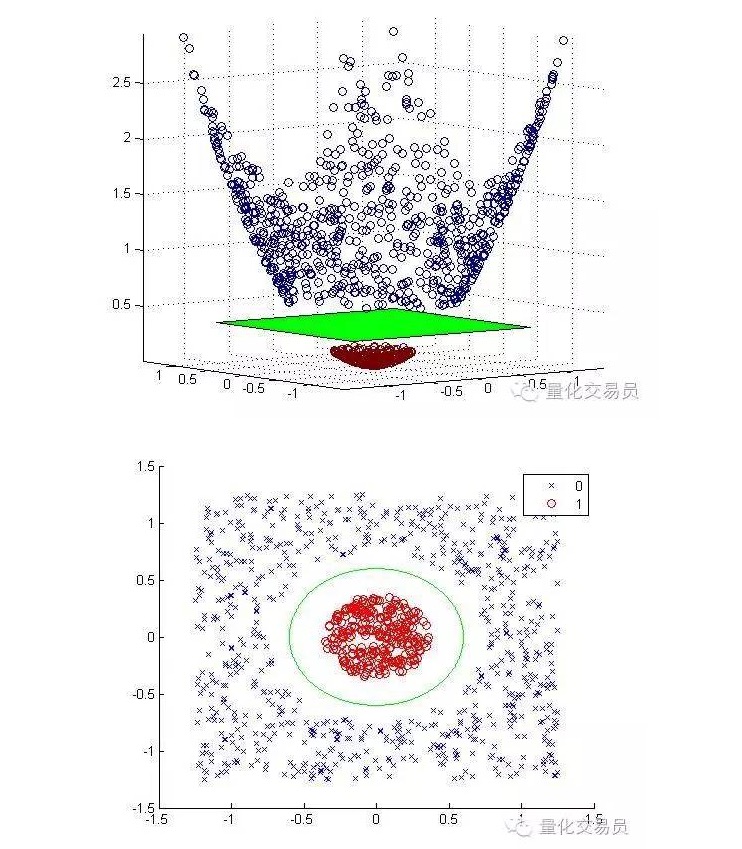
В общем случае, если есть d ввода, вы можете использовать мапировку из d-мерного ввода в p-мерное пространство характеристик. Запустите решение, которое будет получено вышеупомянутым алгоритмом минимизации, и затем отобразите его обратно на p-мерную поверхность вашего первоначального ввода.

Важным условием вышеупомянутого математического решения является то, что оно зависит от того, как создать хороший набор точечных образцов в пространстве признаков.

Вам понадобятся только эти наборы образцов точек для выполнения оптимизации границ, отображение не требует четкости, точки входной пространства в высокомерном пространстве признаков могут быть безопасно рассчитаны с помощью ядерной функции ((и немного теоремы Мерсера)).

Например, вы хотите решить свою классификационную задачу в огромном пространстве характеристик, предположим, 100000 измерений. Можете ли вы представить себе вычислительную мощность, которая вам понадобится? Я очень сомневаюсь, что вы сможете это сделать.

• Вызовы и гориллы

Теперь мы готовимся к тому, чтобы победить Джеффа в его способности предвидеть.

Джефф - эксперт в денежных рынках, он может получить 50%-ную точность прогноза с помощью случайных ставок, которая является сигналом для прогнозирования доходности на следующий торговый день.

Мы будем использовать различные основные временные последовательности, включая временные последовательности цены на месте, прибыль от каждой временной последовательности до 10 лагов, в общей сложности 55 функций.

Мы собираемся построить векторную машину SVM, использующую 3-градусные ядра. Вы можете представить, что выбор подходящего ядра - это еще одна очень сложная задача, чтобы сколифицировать параметры C и Γ, трехкратная перекрестная проверка будет выполняться на сетке из возможных комбинаций параметров, и лучшая группа будет выбрана.

Результаты не очень обнадеживают:

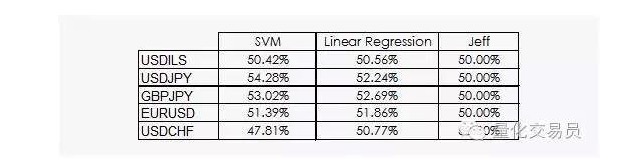
Мы можем видеть, что линейная регрессия и векторные машины SVM могут победить Джеффа. Хотя результаты не являются оптимистичными, мы можем извлечь некоторую информацию из данных, что уже является хорошей новостью, поскольку в области данных финансовые временные последовательности не являются наиболее полезными.

После перекрестной верификации набор данных будет обучен и протестирован, мы запишем прогнозную способность обученного SVM, и для того, чтобы иметь стабильную производительность, мы повторяем случайные деления каждой валюты 1000 раз.

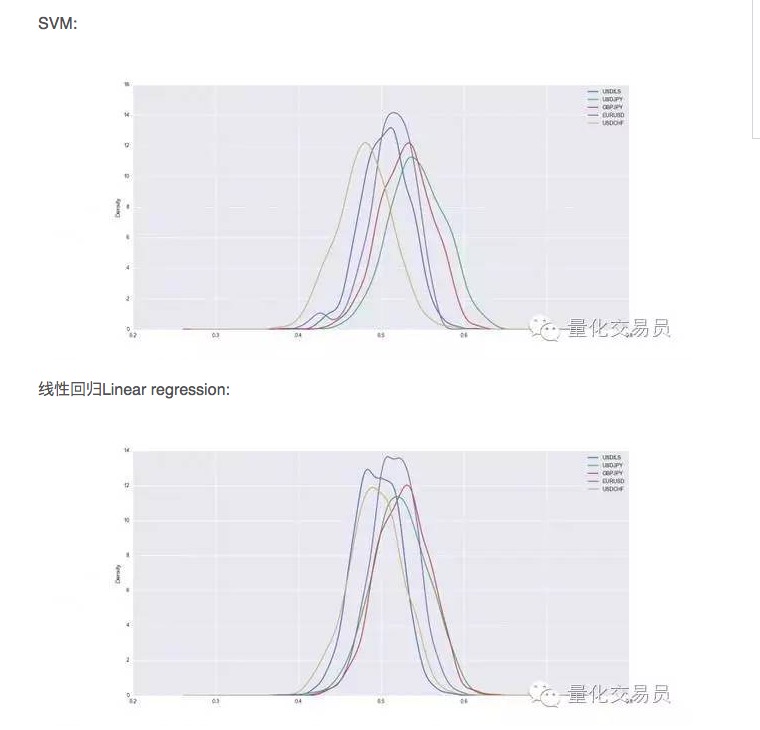
Таким образом, в некоторых случаях SVM превосходит просто линейную регрессию, но и в производительности немного выше. Например, в случае доллара против иена, средний прогнозируемый сигнал составляет 54% от общего числа. Это довольно хороший результат, но давайте посмотрим поближе!

Тед - кузен Джеффа, который, конечно, тоже горилла, но он умнее Джеффа. Тед обращает внимание на тренированный образец, а не на случайные ставки.

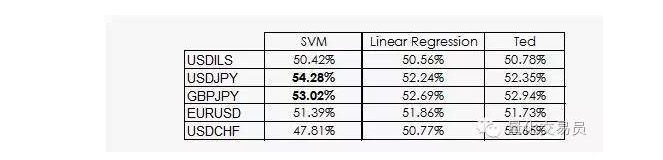
Как мы увидим, большинство SVM-производительности обусловлены лишь тем фактом, что машинное обучение классификации вряд ли будет равняться предыстории. Фактически, линейная регрессия не может получить никакой информации из пространства признаков, но интерфейс (intercept) имеет смысл в регрессии, и это связано с тем, что интерфейс и пересечение более эффективны в определённой классификации.

В лучшем случае, векторальная машина SVM сможет получить дополнительную нелинейную информацию из данных, что позволит нам сделать прогноз с точностью в 2%.

К сожалению, мы пока не знаем, что это за информация, как и то, что у SVM есть свои основные недостатки, которые мы не можем объяснить.

Автор: P. López, опубликовано в Quantdare Копировалось из WeChat Public