В статье в основном рассматриваются стратегии высокочастотной торговли с упором на моделирование совокупного объема и ценовые шоки. В данной статье предлагается предварительная оптимальная модель размещения заказов путем анализа влияния отдельных транзакций, ценовых шоков с фиксированным интервалом и объема транзакций на цены. Эта модель пытается найти оптимальную торговую позицию на основе понимания объемных и ценовых шоков. Подробно обсуждаются предположения модели, а также проводится предварительная оценка оптимального размещения заказа путем сравнения фактической и прогнозируемой моделью ожидаемой доходности.

Моделирование кумулятивного объема

В предыдущей статье было выведено выражение вероятности того, что объем одной транзакции будет больше определенного значения:

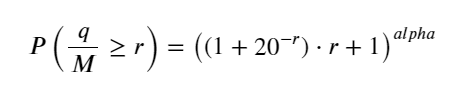
Нас также беспокоит распределение объема торгов за определенный период времени, которое интуитивно должно быть связано с объемом каждой транзакции и частотой ордеров. Далее данные обрабатываются через фиксированные интервалы времени. Постройте график его распределения, как указано выше.

from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

trades = pd.read_csv('HOOKUSDT-aggTrades-2023-01-27.csv')
trades['date'] = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index = trades['date']
buy_trades = trades[trades['is_buyer_maker']==False].copy()
buy_trades = buy_trades.groupby('transact_time').agg({
    'agg_trade_id': 'last',
    'price': 'last',
    'quantity': 'sum',
    'first_trade_id': 'first',
    'last_trade_id': 'last',
    'is_buyer_maker': 'last',
    'date': 'last',
    'transact_time':'last'
})
buy_trades['interval']=buy_trades['transact_time'] - buy_trades['transact_time'].shift()
buy_trades.index = buy_trades['date']

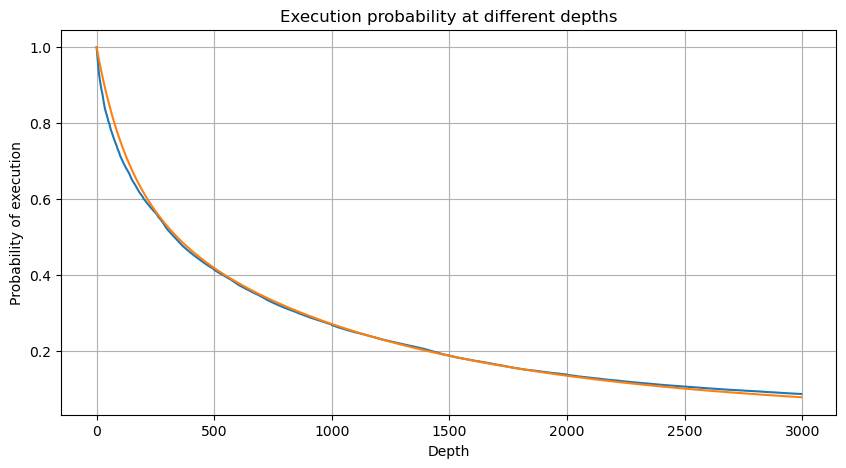
Объедините объем транзакций каждые 1s, удалите часть, где транзакция не произошла, и используйте распределение одной транзакции выше, чтобы подогнать. Видно, что результат лучше. Если все транзакции в течение 1s рассматривать как отдельные транзакции, эта проблема становится Это стало решенной проблемой. Однако при увеличении продолжительности цикла (по сравнению с частотой транзакций) ошибка увеличивается, и исследования показали, что эта ошибка вызвана предыдущим корректирующим членом распределения Парето. Это означает, что по мере удлинения цикла и включения большего количества отдельных транзакций, совокупность множественных транзакций приближается к распределению Парето. В этом случае поправочный член следует удалить.

df_resampled = buy_trades['quantity'].resample('1S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]

buy_trades

	agg_trade_id	price	quantity	first_trade_id	last_trade_id	is_buyer_maker	date	transact_time	interval	diff
2023-01-27 00:00:00.161	1138369	2.901	54.3	3806199	3806201	False	2023-01-27 00:00:00.161	1674777600161	NaN	0.001
2023-01-27 00:00:04.140	1138370	2.901	291.3	3806202	3806203	False	2023-01-27 00:00:04.140	1674777604140	3979.0	0.000
2023-01-27 00:00:04.339	1138373	2.902	55.1	3806205	3806207	False	2023-01-27 00:00:04.339	1674777604339	199.0	0.001
2023-01-27 00:00:04.772	1138374	2.902	1032.7	3806208	3806223	False	2023-01-27 00:00:04.772	1674777604772	433.0	0.000
2023-01-27 00:00:05.562	1138375	2.901	3.5	3806224	3806224	False	2023-01-27 00:00:05.562	1674777605562	790.0	0.000
…	…	…	…	…	…	…	…	…	…	…
2023-01-27 23:59:57.739	1544370	3.572	394.8	5074645	5074651	False	2023-01-27 23:59:57.739	1674863997739	1224.0	0.002
2023-01-27 23:59:57.902	1544372	3.573	177.6	5074652	5074655	False	2023-01-27 23:59:57.902	1674863997902	163.0	0.001
2023-01-27 23:59:58.107	1544373	3.573	139.8	5074656	5074656	False	2023-01-27 23:59:58.107	1674863998107	205.0	0.000
2023-01-27 23:59:58.302	1544374	3.573	60.5	5074657	5074657	False	2023-01-27 23:59:58.302	1674863998302	195.0	0.000
2023-01-27 23:59:59.894	1544376	3.571	12.1	5074662	5074664	False	2023-01-27 23:59:59.894	1674863999894	1592.0	0.000

#1s内的累计分布
depths = np.array(range(0, 3000, 5))
probabilities = np.array([np.mean(df_resampled['quantity'] > depth) for depth in depths])
mean = df_resampled['quantity'].mean()
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([((1+20**(-depth/mean))*depth/mean+1)**(alpha) for depth in depths])

plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)

df_resampled = buy_trades['quantity'].resample('30S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
depths = np.array(range(0, 12000, 20))
probabilities = np.array([np.mean(df_resampled['quantity'] > depth) for depth in depths])
mean = df_resampled['quantity'].mean()
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([((1+20**(-depth/mean))*depth/mean+1)**(alpha) for depth in depths])
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2)
probabilities_s_2 = np.array([(depth/mean+1)**alpha for depth in depths]) # 无修正

plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities,label='Probabilities (True)')
plt.plot(depths, probabilities_s, label='Probabilities (Simulation 1)')
plt.plot(depths, probabilities_s_2, label='Probabilities (Simulation 2)')
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.legend() 
plt.grid(True)

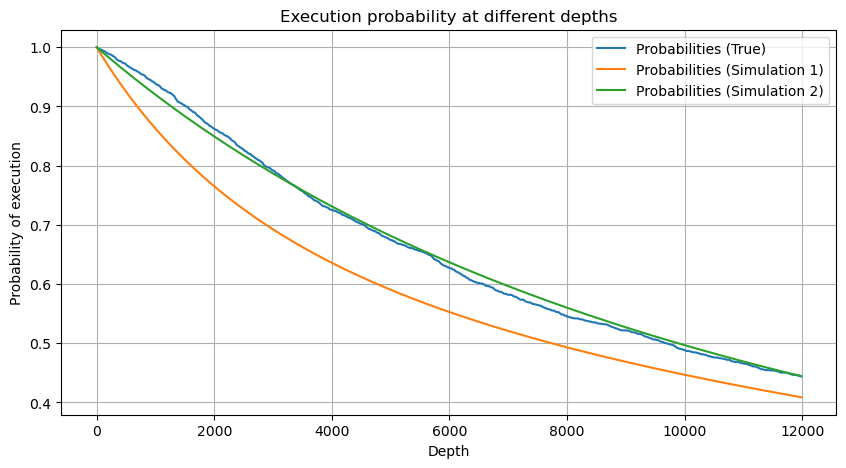
Теперь мы вывели общую формулу распределения накопленного объема торгов в разное время и использовали распределение отдельных транзакций для ее подгонки, без необходимости подсчитывать их каждый раз по отдельности. Здесь мы опускаем процесс и приводим формулу напрямую:

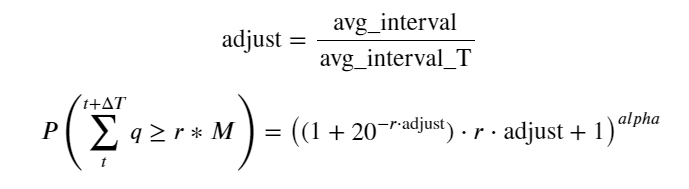
Среди них avg_interval представляет собой средний интервал между отдельными транзакциями, а avg_interval_T представляет собой средний интервал интервалов, которые необходимо оценить. Это немного сбивает с толку. Если мы хотим оценить время транзакции в 1 секунду, нам необходимо рассчитать средний интервал между событиями, содержащими транзакции в течение 1 секунды. Если вероятность поступления заказа соответствует распределению Пуассона, то ее можно оценить непосредственно здесь, но фактическое отклонение велико, поэтому я не буду его здесь объяснять.

Обратите внимание, что вероятность того, что объем будет больше определенного значения в пределах определенного интервала, должна существенно отличаться от фактической вероятности транзакции в этой позиции в глубине, поскольку чем дольше время ожидания, тем больше вероятность того, что книга ордеров меняется, и транзакция также приводит к изменению глубины, поэтому вероятность транзакции на одной и той же глубинной позиции изменяется в реальном времени по мере обновления данных.

df_resampled = buy_trades['quantity'].resample('2S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
depths = np.array(range(0, 6500, 10))
probabilities = np.array([np.mean(df_resampled['quantity'] > depth) for depth in depths])
mean = buy_trades['quantity'].mean()
adjust = buy_trades['interval'].mean() / 2620
alpha = np.log(np.mean(buy_trades['quantity'] > mean))/0.7178397931503168
probabilities_s = np.array([((1+20**(-depth*adjust/mean))*depth*adjust/mean+1)**(alpha) for depth in depths])

plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)

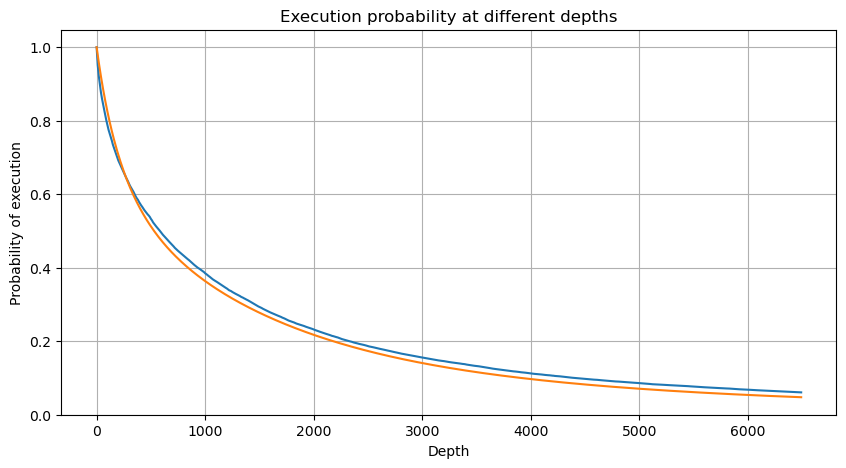
Влияние цены на единичную транзакцию

Данные о транзакциях — это сокровище, и их еще очень много предстоит извлечь. Следует обратить пристальное внимание на влияние ордеров на цены, что влияет на размещение отложенных ордеров в стратегии. Аналогично, на основе данных агрегата transact_time, вычислите разницу между последней ценой и первой ценой. Если есть только один заказ, разница равна 0. Странно, что все еще есть небольшое количество результатов данных с отрицательными результатами. Это должно быть проблемой порядка расположения данных, поэтому я не буду вдаваться в подробности.

Результаты показывают, что доля отсутствия воздействия достигает 77%, доля 1 тика составляет 16,5%, 2 тика — 3,7%, 3 тика — 1,2%, а доля более 4 тика составляет менее 1%. . Это в основном соответствует характеристикам экспоненциальной функции, но подгонка не точна.

Объем транзакций, вызвавший соответствующую разницу в цене, был подсчитан, а искажение, вызванное слишком большим воздействием, было удалено. В основном это соответствует линейной зависимости, и примерно каждые 1000 объемов вызывают колебание цены на 1 тик. Также можно предположить, что среднее количество отложенных ордеров около каждой цены составляет около 1000.

diff_df = trades[trades['is_buyer_maker']==False].groupby('transact_time')['price'].agg(lambda x: abs(round(x.iloc[-1] - x.iloc[0],3)) if len(x) > 1 else 0)
buy_trades['diff'] = buy_trades['transact_time'].map(diff_df)

diff_counts = buy_trades['diff'].value_counts()
diff_counts[diff_counts>10]/diff_counts.sum()

0.000    0.769965
0.001    0.165527
0.002    0.037826
0.003    0.012546
0.004    0.005986
0.005    0.003173
0.006    0.001964
0.007    0.001036
0.008    0.000795
0.009    0.000474
0.010    0.000227
0.011    0.000187
0.012    0.000087
0.013    0.000080
Name: diff, dtype: float64

diff_group = buy_trades.groupby('diff').agg({
    'quantity': 'mean',
    'diff': 'last',
})

diff_group['quantity'][diff_group['diff']>0][diff_group['diff']<0.01].plot(figsize=(10,5),grid=True);

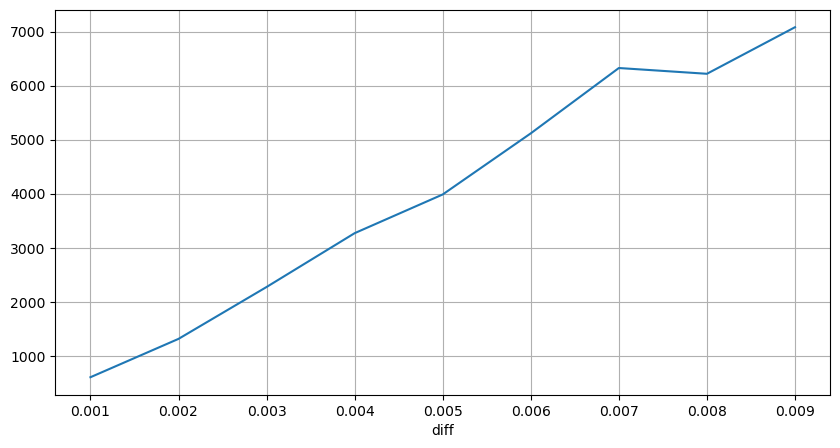
Ценовые шоки через регулярные промежутки времени

Посчитайте влияние цены в течение 2 секунд. Разница здесь в том, что будут отрицательные значения. Конечно, поскольку здесь учитываются только ордера на покупку, симметричная позиция будет на один тик больше. Продолжайте наблюдать за связью между объемом торговли и влиянием и учитывайте только результаты больше 0. Вывод аналогичен выводу для одного ордера, который также является приблизительно линейной зависимостью. Каждый тик требует примерно 2000 объема.

df_resampled = buy_trades.resample('2S').agg({ 
    'price': ['first', 'last', 'count'],
    'quantity': 'sum'
})
df_resampled['price_diff'] = round(df_resampled[('price', 'last')] - df_resampled[('price', 'first')],3)
df_resampled['price_diff'] = df_resampled['price_diff'].fillna(0)
result_df_raw = pd.DataFrame({
    'price_diff': df_resampled['price_diff'],
    'quantity_sum': df_resampled[('quantity', 'sum')],
    'data_count': df_resampled[('price', 'count')]
})
result_df = result_df_raw[result_df_raw['price_diff'] != 0]

result_df['price_diff'][abs(result_df['price_diff'])<0.016].value_counts().sort_index().plot.bar(figsize=(10,5));

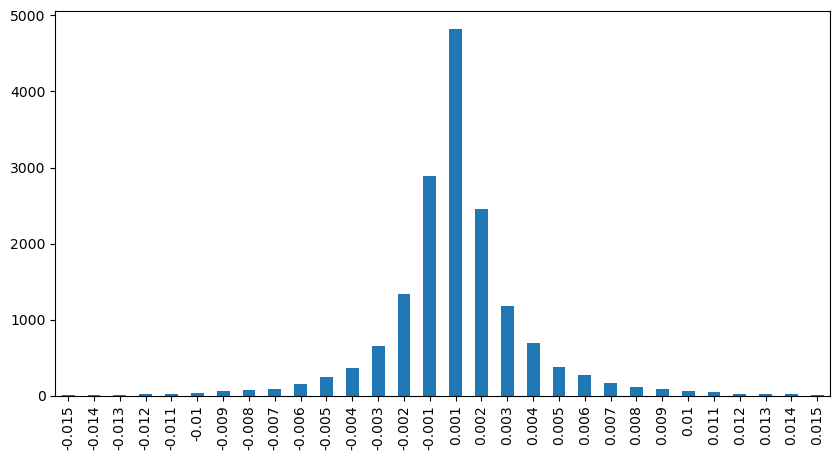
result_df['price_diff'].value_counts()[result_df['price_diff'].value_counts()>30]

 0.001    7176
-0.001    3665
 0.002    3069
-0.002    1536
 0.003    1260
 0.004     692
-0.003     608
 0.005     391
-0.004     322
 0.006     259
-0.005     192
 0.007     146
-0.006     112
 0.008      82
 0.009      75
-0.007      75
-0.008      65
 0.010      51
 0.011      41
-0.010      31
Name: price_diff, dtype: int64

diff_group = result_df.groupby('price_diff').agg({ 'quantity_sum': 'mean'})

diff_group[(diff_group.index>0) & (diff_group.index<0.015)].plot(figsize=(10,5),grid=True);

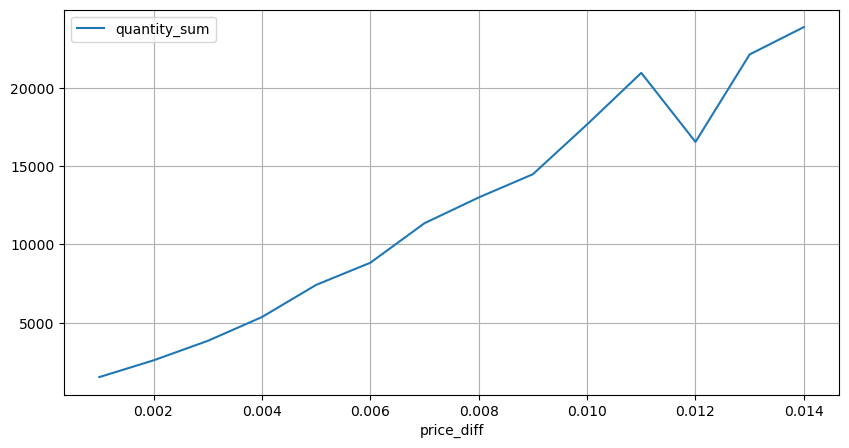
Ценовое влияние объема

Объем, необходимый для изменения тика, был рассчитан ранее, но он неточен, поскольку основан на предположении, что воздействие уже произошло. Теперь давайте рассмотрим влияние объема торгов на цену.

Данные здесь выбираются с интервалом в 1 секунду, при этом 100 величин являются одним шагом, и подсчитываются изменения цен в пределах этого диапазона величин. Были сделаны некоторые ценные выводы:

1. Когда объем покупки ниже 500, ожидаемое изменение цены снижается, что ожидаемо, поскольку на цену также влияют ордера на продажу.
2. При низком объеме торгов наблюдается линейная зависимость: чем больше объем торгов, тем больше рост цен.
3. Чем больше объем ордера на покупку, тем больше изменение цены, что часто представляет собой прорыв цены. После прорыва цена может вернуться. В сочетании с выборкой через фиксированные интервалы данные нестабильны.
4. Следует обратить внимание на верхнюю часть диаграммы рассеяния, то есть на ту часть, где объем соответствует росту цены.
5. Только для этой торговой пары приводится приблизительная версия взаимосвязи между объемом и изменением цены:

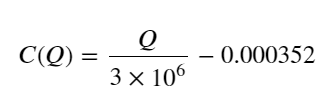
Среди них «C» представляет собой изменение цены, а «Q» — объем ордера на покупку.

df_resampled = buy_trades.resample('1S').agg({ 
    'price': ['first', 'last', 'count'],
    'quantity': 'sum'
})
df_resampled['price_diff'] = round(df_resampled[('price', 'last')] - df_resampled[('price', 'first')],3)
df_resampled['price_diff'] = df_resampled['price_diff'].fillna(0)
result_df_raw = pd.DataFrame({
    'price_diff': df_resampled['price_diff'],
    'quantity_sum': df_resampled[('quantity', 'sum')],
    'data_count': df_resampled[('price', 'count')]
})
result_df = result_df_raw[result_df_raw['price_diff'] != 0]

df = result_df.copy()
bins = np.arange(0, 30000, 100)  # 
labels = [f'{i}-{i+100-1}' for i in bins[:-1]]  
df.loc[:, 'quantity_group'] = pd.cut(df['quantity_sum'], bins=bins, labels=labels)
grouped = df.groupby('quantity_group')['price_diff'].mean()

grouped_df = pd.DataFrame(grouped).reset_index()
grouped_df['quantity_group_center'] = grouped_df['quantity_group'].apply(lambda x: (float(x.split('-')[0]) + float(x.split('-')[1])) / 2)

plt.figure(figsize=(10,5))
plt.scatter(grouped_df['quantity_group_center'], grouped_df['price_diff'],s=10)
plt.plot(grouped_df['quantity_group_center'], np.array(grouped_df['quantity_group_center'].values)/2e6-0.000352,color='red')
plt.xlabel('quantity_group_center')
plt.ylabel('average price_diff')
plt.title('Scatter plot of average price_diff by quantity_group')
plt.grid(True)

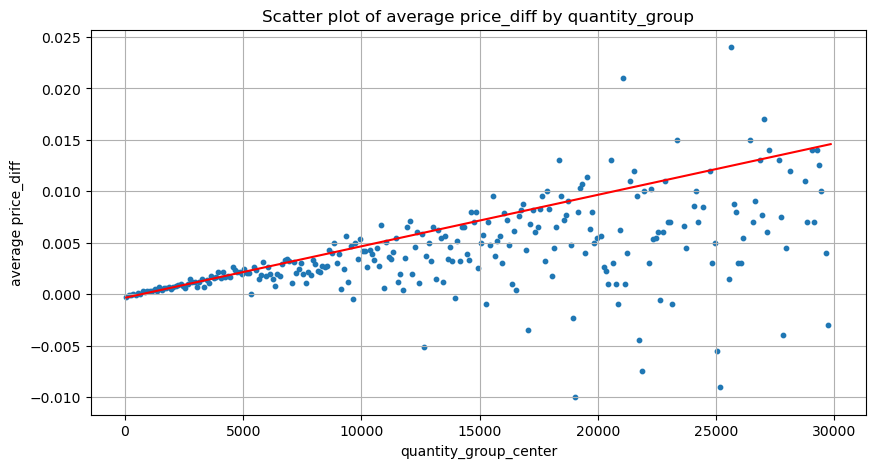
grouped_df.head(10)

	quantity_group	price_diff	quantity_group_center
0	0-199	-0.000302	99.5
1	100-299	-0.000124	199.5
2	200-399	-0.000068	299.5
3	300-499	-0.000017	399.5
4	400-599	-0.000048	499.5
5	500-699	0.000098	599.5
6	600-799	0.000006	699.5
7	700-899	0.000261	799.5
8	800-999	0.000186	899.5
9	900-1099	0.000299	999.5

Начальная оптимальная позиция заказа

С помощью моделирования объема торгов и приблизительной модели объема торгов, соответствующей влиянию цены, можно рассчитать оптимальную позицию ордера. Давайте сделаем несколько предположений и дадим безответственную оптимальную ценовую позицию.

1. Предположим, что цена возвращается к своему первоначальному значению после шока (это, конечно, маловероятно и требует повторного анализа изменения цены после шока).
2. Предположим, что распределение объема торгов и частоты ордеров в течение этого периода соответствует заданным требованиям (это также неточно, поскольку для оценки используется значение одного дня, а транзакции имеют очевидную кластеризацию).
3. Предположим, что за время моделирования поступает только один ордер на продажу, после чего позиция закрывается.
4. Предполагая, что после исполнения ордера, есть другие ордера на покупку, которые продолжат толкать цену вверх, особенно когда объем очень низок. Этот эффект здесь игнорируется, и просто предполагается, что он вернется.

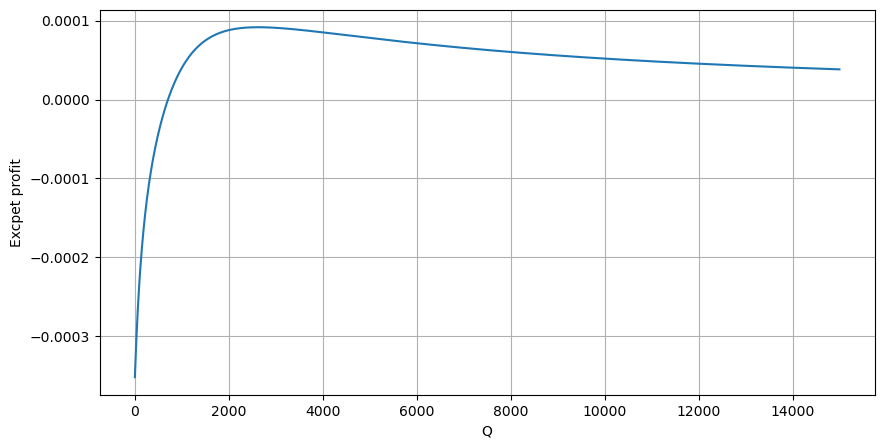
Сначала запишите простую ожидаемую доходность, то есть вероятность того, что совокупный ордер на покупку превысит Q в течение 1 секунды, умноженную на ожидаемую норму доходности (то есть на цену влияния):

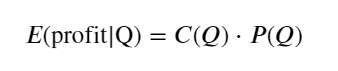
Согласно графику, ожидаемая доходность максимальна на уровне около 2500, что примерно в 2,5 раза превышает средний объем торгов. То есть ордер на продажу следует разместить на уровне 2500. Необходимо еще раз подчеркнуть, что горизонтальная ось отображает объем торговли за 1 секунду и не может быть просто приравнена к глубине позиции. И это в то время, когда по-прежнему не хватает очень важных подробных данных, и они основаны только на предположениях, основанных на сделках.

Подвести итог

Установлено, что распределение объема на разных временных интервалах представляет собой простое масштабирование распределения объема одной транзакции. Мы также создали простую модель ожидаемой доходности на основе ценовых шоков и вероятности транзакции. Результаты этой модели соответствуют нашим ожиданиям. Если объем ордера на продажу небольшой, это указывает на падение цены. Определенный объем требуется для имеют маржу прибыли, и чем больше объем транзакции, тем выше маржа прибыли. Чем больше вероятность, тем она ниже. В середине есть оптимальный размер, который также является позицией размещения ордера, которую ищет стратегия. Конечно, эта модель пока слишком проста. В следующей статье я продолжу ее подробное обсуждение.

#1s内的累计分布
df_resampled = buy_trades['quantity'].resample('1S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]

depths = np.array(range(0, 15000, 10))
mean = df_resampled['quantity'].mean()
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([((1+20**(-depth/mean))*depth/mean+1)**(alpha) for depth in depths])
profit_s = np.array([depth/2e6-0.000352 for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities_s*profit_s)
plt.xlabel('Q')
plt.ylabel('Excpet profit')
plt.grid(True)