اعلی تعدد تجارتی حکمت عملی کے بارے میں خیالات (1)
 3
3
 4856
4856

مضمون میں ڈیجیٹل کرنسیوں کی اعلی تعدد والی تجارتی حکمت عملیوں پر تبادلہ خیال کیا گیا ہے، بشمول منافع کے ذرائع (بنیادی طور پر مارکیٹ کے اتار چڑھاؤ اور ایکسچینج فیس میں چھوٹ)، آرڈر پلیسمنٹ اور پوزیشن کنٹرول کے مسائل، اور پیریٹو ڈسٹری بیوشن کا استعمال کرتے ہوئے تجارتی حجم کی ماڈلنگ کا طریقہ۔ اس کے علاوہ، Binance کی طرف سے فراہم کردہ لین دین اور بہترین آرڈر کے اعداد و شمار کو بیک ٹیسٹنگ کے لیے استعمال کیا گیا، اور اعلی تعدد والی تجارتی حکمت عملیوں کے دیگر مسائل کو بعد کے مضامین میں گہرائی میں زیر بحث لانے کا منصوبہ بنایا گیا ہے۔
میں نے اس سے پہلے ڈیجیٹل کرنسیوں کی ہائی فریکوئنسی ٹریڈنگ کے بارے میں دو مضامین لکھے ہیں۔ ڈیجیٹل کرنسیوں کے لیے اعلی تعدد کی حکمت عملیوں کا تفصیلی تعارف, 5 دنوں میں 80 بار کمائیں، اعلی تعدد حکمت عملی کی طاقت. لیکن اسے صرف تجربے اور عمومی باتوں کا اشتراک قرار دیا جا سکتا ہے۔ اس بار میں شروع سے ہی اعلی تعدد ٹریڈنگ کے خیالات کو متعارف کرانے کے لیے مضامین لکھنے کا ارادہ رکھتا ہوں، تاہم، میری محدود سطح اور اعلی تعدد کی گہرائی کی وجہ سے ٹریڈنگ، یہ مضمون صرف ایک نقطہ آغاز ہے مجھے امید ہے کہ ماہرین مجھے درست کر سکتے ہیں۔
اعلی تعدد منافع کے ذرائع
جیسا کہ پچھلے مضامین میں ذکر کیا گیا ہے، اعلی تعدد کی حکمت عملی انتہائی اتار چڑھاؤ والی مارکیٹوں کے لیے خاص طور پر موزوں ہے۔ مختصر مدت میں تجارتی مصنوعات کی قیمتوں میں تبدیلیوں کا جائزہ لیں، جو مجموعی رجحانات اور اتار چڑھاو پر مشتمل ہوتا ہے۔ اگر ہم رجحانات میں ہونے والی تبدیلیوں کا درست اندازہ لگا سکتے ہیں، تو ہم یقینی طور پر پیسہ کما سکتے ہیں، لیکن یہ سب سے مشکل بھی ہے، یہ مضمون بنیادی طور پر ہائی فریکوئنسی بنانے والی حکمت عملیوں کو متعارف کرایا گیا ہے اور اس میں یہ مسئلہ شامل نہیں ہوگا۔ اتار چڑھاؤ والی مارکیٹ میں، اگر آرڈرز اوپر اور نیچے کرنے کی حکمت عملی کو کثرت سے انجام دیا جاتا ہے اور منافع کا مارجن کافی زیادہ ہے، تو یہ رجحان کی وجہ سے ہونے والے ممکنہ نقصانات کو پورا کر سکتا ہے، تاکہ آپ مارکیٹ کی پیش گوئی کیے بغیر منافع کما سکیں۔ فی الحال، ایکسچینجز پر تمام میکر ٹرانزیکشنز کو لین دین کی فیس پر چھوٹ ملتی ہے، جو کہ منافع کا ایک جزو ہے، مقابلہ جتنا زیادہ ہوگا، چھوٹ کا تناسب اتنا ہی زیادہ ہونا چاہیے۔
مسئلہ حل ہونا ہے۔
حکمت عملی ایک ہی وقت میں آرڈرز خریدتی ہے اور آرڈر بیچتی ہے، پہلا سوال یہ ہے کہ آرڈر کہاں پر دئیے جائیں۔ آرڈر جتنا قریب ہو گا، لین دین کا امکان اتنا ہی زیادہ ہو گا، تاہم، ایک غیر مستحکم مارکیٹ میں، فوری طور پر لین دین کی قیمت مارکیٹ سے بہت دور ہو سکتی ہے، آپ اس قابل نہیں ہوں گے۔ کافی منافع حاصل کریں. بہت دور رکھے گئے احکامات پر عمل درآمد کا امکان کم ہے۔ یہ ایک ایسا مسئلہ ہے جس کی اصلاح کی ضرورت ہے۔
اپنی پوزیشن کو کنٹرول کریں۔ خطرات کو کنٹرول کرنے کے لیے، حکمت عملی طویل عرصے تک بہت زیادہ پوزیشنیں جمع نہیں کر سکتی۔ اسے آرڈر کی دوری، آرڈر کی مقدار، کل پوزیشن کی حد، وغیرہ کو کنٹرول کرکے حل کیا جاسکتا ہے۔
مندرجہ بالا اہداف کو حاصل کرنے کے لیے، لین دین کے امکان، لین دین کے منافع، مارکیٹ کا تخمینہ اور دیگر پہلوؤں کا نمونہ اور اندازہ لگانا ضروری ہے، اس شعبے میں بہت سے مضامین اور کاغذات ہیں، جو کہ ہائی فریکونسی ٹریڈنگ جیسے مطلوبہ الفاظ کے ساتھ مل سکتے ہیں۔ ، آرڈر بک، وغیرہ بہت ساری سفارشات آن لائن ہیں، جن میں میں یہاں نہیں جاؤں گا۔ اس کے علاوہ، ایک قابل بھروسہ اور تیز رفتار بیک ٹیسٹنگ سسٹم قائم کرنا بہتر ہے اگرچہ حقیقی ٹریڈنگ کے ذریعے ان کی تاثیر کی تصدیق کی جا سکتی ہے، بیک ٹیسٹنگ اب بھی مزید آئیڈیاز فراہم کر سکتی ہے اور آزمائش اور غلطی کی لاگت کو کم کر سکتی ہے۔
مطلوبہ ڈیٹا
بائننس لین دین بہ لین دین اور بہترین آرڈر ڈیٹا فراہم کرتا ہے۔ڈاؤن لوڈ کریں,وائٹ لسٹ میں API کا استعمال کرتے ہوئے گہرے ڈیٹا کو ڈاؤن لوڈ کرنے کی ضرورت ہے، یا آپ اسے خود جمع کر سکتے ہیں۔ بیک ٹیسٹنگ کے مقاصد کے لیے، آپ صرف جمع کردہ لین دین کا ڈیٹا استعمال کر سکتے ہیں۔ یہ مضمون مثال کے طور پر HOOKUSDT-aggTrades-2023-01-27 کا ڈیٹا لیتا ہے۔
from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
لین دین کے کالم درج ذیل ہیں:
- agg_trade_id: مجموعی ٹرانزیکشن آرڈر کی id،
- قیمت: لین دین کی قیمت
- مقدار: لین دین کی تعداد
- first_trade_id: جمع میں ایک ہی وقت میں کئی ٹرانزیکشنز ہو سکتے ہیں، صرف ایک ڈیٹا شمار کیا جاتا ہے، یہ پہلی ٹرانزیکشن کی آئی ڈی ہے
- last_trade_id: آخری لین دین کی شناخت
- transact_time: لین دین کا وقت
- is_buyer_maker: لین دین کی سمت، صحیح کا مطلب ہے کہ خرید آرڈر بنانے والے کی طرف سے تجارت کی جاتی ہے، اور فروخت کے آرڈر کی تجارت لینے والے کے ذریعے کی جاتی ہے
یہ دیکھا جا سکتا ہے کہ اس دن 660,000 ٹرانزیکشن ڈیٹا تھے، اور لین دین بہت فعال تھے۔ csv تبصرے کے سیکشن میں منسلک کیا جائے گا۔
trades = pd.read_csv('COMPUSDT-aggTrades-2023-07-02.csv')
trades
664475 rows × 7 columns
| agg_trade_id | price | quantity | first_trade_id | last_trade_id | transact_time | is_buyer_maker |
|---|---|---|---|---|---|---|
| 120719552 | 52.42 | 22.087 | 207862988 | 207862990 | 1688256004603 | False |
| 120719553 | 52.41 | 29.314 | 207862991 | 207863002 | 1688256004623 | True |
| 120719554 | 52.42 | 0.945 | 207863003 | 207863003 | 1688256004678 | False |
| 120719555 | 52.41 | 13.534 | 207863004 | 207863006 | 1688256004680 | True |
| … | … | … | … | … | … | … |
| 121384024 | 68.29 | 10.065 | 210364899 | 210364905 | 1688342399863 | False |
| 121384025 | 68.30 | 7.078 | 210364906 | 210364908 | 1688342399948 | False |
| 121384026 | 68.29 | 7.622 | 210364909 | 210364911 | 1688342399979 | True |
سنگل ٹرانزیکشن والیوم ماڈلنگ
سب سے پہلے، ڈیٹا پر کارروائی کریں اور اصل تجارت کو خرید آرڈر ایکٹیو ٹرانزیکشن گروپ اور سیل آرڈر ایکٹیو ٹرانزیکشن گروپ میں تقسیم کریں۔ اس کے علاوہ، اصل مجموعی لین دین کا ڈیٹا ایک ہی وقت میں، ایک ہی قیمت پر اور ایک ہی سمت میں 100 کا ایک فعال خرید آرڈر ہو سکتا ہے۔ اگر اسے مختلف قیمتوں کے ساتھ متعدد لین دین میں تقسیم کیا گیا ہو، جیسے۔ 60 اور 40 کے طور پر، ڈیٹا کے دو ٹکڑے تیار کیے جائیں گے، جو خرید آرڈر کے حجم کے تخمینے کو متاثر کرے گا۔ لہذا، transact_time کی بنیاد پر دوبارہ جمع کرنا ضروری ہے۔ جمع کرنے کے بعد، ڈیٹا کی مقدار میں 140,000 ریکارڈ کی کمی ہوئی۔
trades['date'] = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index = trades['date']
buy_trades = trades[trades['is_buyer_maker']==False].copy()
sell_trades = trades[trades['is_buyer_maker']==True].copy()
buy_trades = buy_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
sell_trades = sell_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
buy_trades['interval']=buy_trades['transact_time'] - buy_trades['transact_time'].shift()
sell_trades['interval']=sell_trades['transact_time'] - sell_trades['transact_time'].shift()
print(trades.shape[0] - (buy_trades.shape[0]+sell_trades.shape[0]))
146181
خرید آرڈرز کو مثال کے طور پر لے کر، آپ دیکھ سکتے ہیں کہ لمبی دم کا اثر بہت واضح ہے، لیکن ٹیل پر بہت کم لین دین تقسیم کیے گئے ہیں۔ .
buy_trades['quantity'].plot.hist(bins=200,figsize=(10, 5));
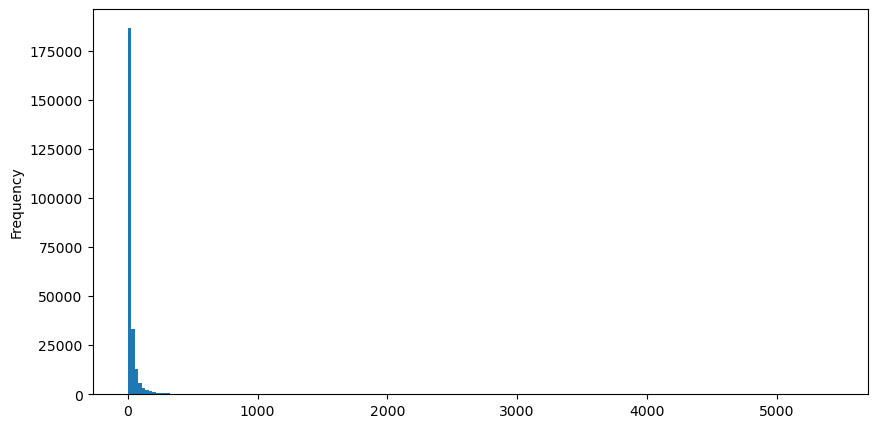
مشاہدے کی سہولت کے لیے، ہم دم کو کاٹتے ہیں اور مشاہدہ کرتے ہیں کہ تجارتی حجم جتنا زیادہ ہوگا، وقوع پذیر ہونے کی تعدد اتنی ہی کم ہوگی، اور تیزی سے کمی کا رجحان ہوگا۔
buy_trades['quantity'][buy_trades['quantity']<200].plot.hist(bins=200,figsize=(10, 5));
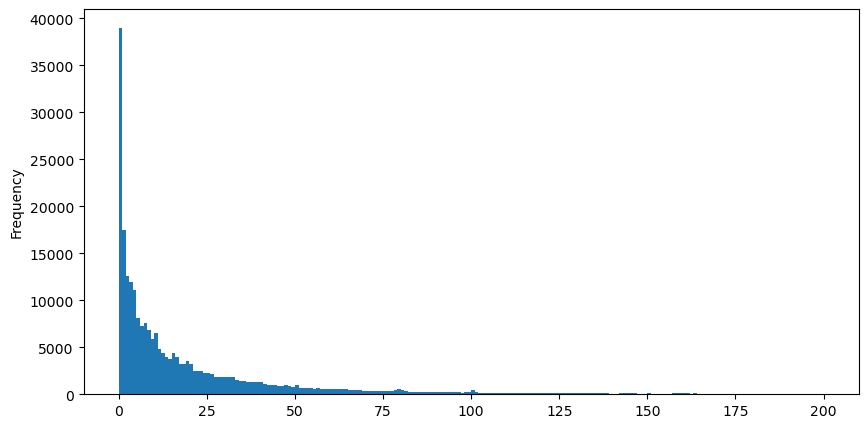
حجم اطمینان کی تقسیم پر بہت سے مطالعہ ہیں. اس کی طاقت کے قانون کی تقسیم کو Pareto تقسیم بھی کہا جاتا ہے، جو شماریاتی طبیعیات اور سماجی علوم میں امکانی تقسیم کی ایک عام شکل ہے۔ پاور لا ڈسٹری بیوشن میں، کسی خاص سائز (یا فریکوئنسی) کے ایونٹ کا امکان اس ایونٹ کے سائز کے کچھ منفی ایکسپونٹ کے متناسب ہوتا ہے۔ اس تقسیم کے فارم کی اہم خصوصیت یہ ہے کہ بڑے واقعات (یعنی وہ جو کہ وسط سے دور ہیں) اس سے کہیں زیادہ کثرت سے رونما ہوتے ہیں جس کی توقع بہت سی دوسری تقسیموں میں کی جاتی ہے۔ یہ تجارتی حجم کی تقسیم کی خصوصیت ہے۔ Pareto کی تقسیم کی شکل ہے: P(x) = Cx^(-α)۔ یہ ذیل میں دکھایا جائے گا.
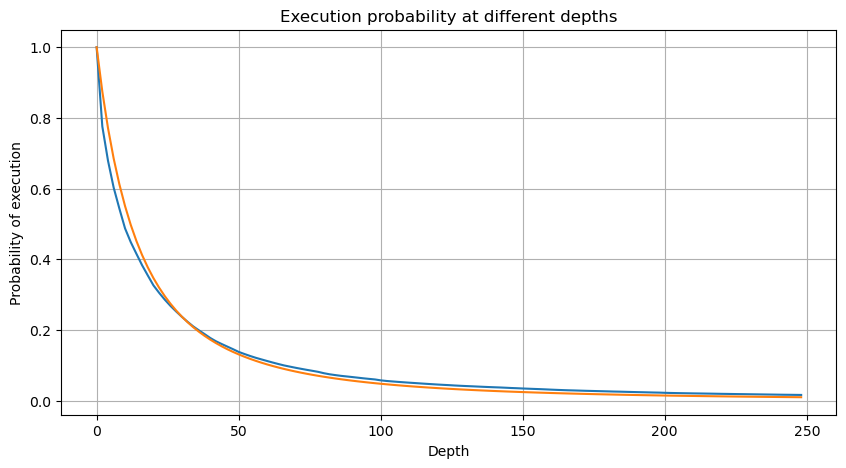
نیچے دی گئی تصویر اس امکان کو ظاہر کرتی ہے کہ تجارتی حجم ایک خاص قدر سے زیادہ ہے، اور اورنج لائن اس بات کا امکان ہے کہ مخصوص پیرامیٹرز کے بارے میں فکر نہ کریں۔ Pareto کی تقسیم کو پورا کریں۔ چونکہ آرڈر کا حجم 0 سے زیادہ ہونے کا امکان 1 ہے، اور معیاری کاری کے تقاضوں کو پورا کرنے کے لیے، تقسیم کی مساوات درج ذیل ہونی چاہیے:
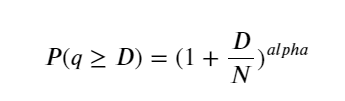
جہاں N معیاری پیرامیٹر ہے۔ یہاں ہم اوسط حجم M اور الفا -2.06 کو منتخب کرتے ہیں۔ الفا کا مخصوص تخمینہ الٹا حساب لگا کر لگایا جا سکتا ہے P قدر جب D=N۔ خاص طور پر: alpha = log(P(d>M))/log(2) ۔ مختلف پوائنٹس کا انتخاب کرنے سے الفا قدریں قدرے مختلف ہوں گی۔
depths = range(0, 250, 2)
probabilities = np.array([np.mean(buy_trades['quantity'] > depth) for depth in depths])
alpha = np.log(np.mean(buy_trades['quantity'] > mean_quantity))/np.log(2)
mean_quantity = buy_trades['quantity'].mean()
probabilities_s = np.array([(1+depth/mean_quantity)**alpha for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)
plt.figure(figsize=(10, 5))
plt.grid(True)
plt.title('Diff')
plt.plot(depths, probabilities_s-probabilities);
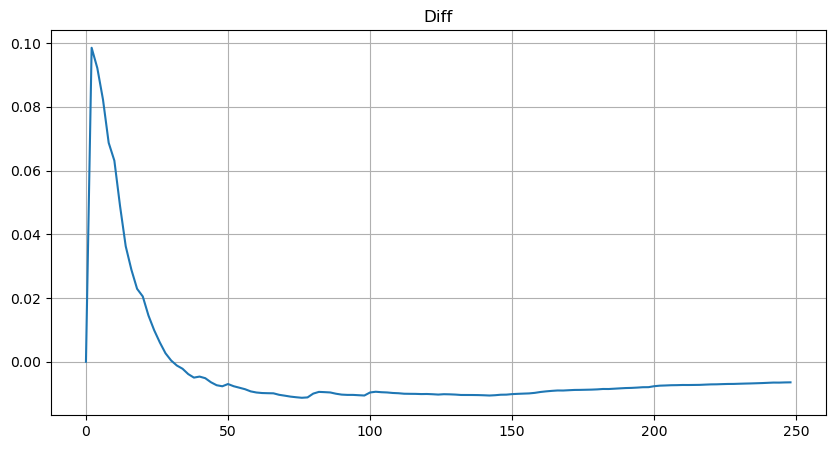
لیکن یہ تخمینہ صرف ایسا لگتا ہے جیسا کہ اوپر دی گئی تصویر میں، ہم نقلی قدر اور اصل قدر کے درمیان فرق کو پلاٹ کرتے ہیں۔ جب تجارتی حجم چھوٹا ہوتا ہے تو انحراف بڑا ہوتا ہے، یہاں تک کہ 10% کے قریب۔ پیرامیٹر کے تخمینے کے دوران مختلف پوائنٹس کو منتخب کرکے نقطہ کے امکان کو زیادہ درست بنایا جاسکتا ہے، لیکن اس سے انحراف کا مسئلہ حل نہیں ہوتا ہے۔ یہ طاقت کے قانون کی تقسیم اور حقیقی تقسیم کے درمیان فرق سے طے ہوتا ہے، زیادہ درست نتائج حاصل کرنے کے لیے، طاقت کے قانون کی تقسیم کی مساوات کو درست کرنے کی ضرورت ہے۔ میں مخصوص عمل کے بارے میں تفصیل میں نہیں جاؤں گا، لیکن مجھے ایک الہام ہوا اور مجھے معلوم ہوا کہ یہ درحقیقت مندرجہ ذیل ہونا چاہیے:
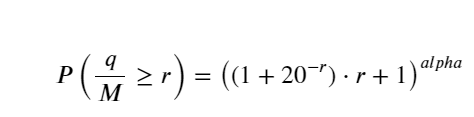
سادگی کے لیے، معیاری تجارتی حجم کی نمائندگی کرنے کے لیے یہاں r = q/M استعمال کیا جاتا ہے۔ پیرامیٹرز کا اندازہ اوپر کی طرح ہی لگایا جا سکتا ہے۔ مندرجہ ذیل اعداد و شمار سے پتہ چلتا ہے کہ تصحیح کے بعد زیادہ سے زیادہ انحراف 2% سے زیادہ نہیں ہے، اصلاح جاری رکھی جا سکتی ہے، لیکن یہ درستگی کافی ہے۔
depths = range(0, 250, 2)
probabilities = np.array([np.mean(buy_trades['quantity'] > depth) for depth in depths])
mean = buy_trades['quantity'].mean()
alpha = np.log(np.mean(buy_trades['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([(((1+20**(-depth/mean))*depth+mean)/mean)**alpha for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)
plt.figure(figsize=(10, 5))
plt.grid(True)
plt.title('Diff')
plt.plot(depths, probabilities_s-probabilities);
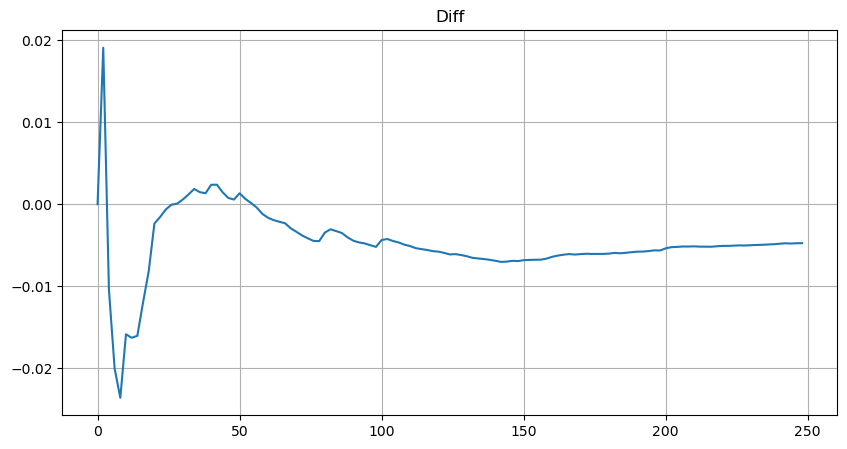
حجم کی تقسیم کے لیے تخمینی مساوات کے ساتھ، نوٹ کریں کہ مساوات کا امکان حقیقی امکان نہیں ہے، بلکہ ایک مشروط امکان ہے۔ اس مقام پر ہم اس سوال کا جواب دے سکتے ہیں: اگر اگلا حکم آتا ہے، تو اس بات کا کیا امکان ہے کہ یہ ترتیب ایک خاص قدر سے زیادہ ہے؟ دوسرے لفظوں میں، مختلف گہرائیوں کے احکامات پر عمل درآمد کا کیا امکان ہے (مثالی صورت حال، اتنی سخت نہیں، تھیوری میں آرڈر بک میں نئے آرڈرز اور کینسلیشنز کے ساتھ ساتھ ایک ہی گہرائی میں قطاریں ہیں)۔
مضمون یہاں تقریباً ختم ہو چکا ہے، اور ابھی بھی بہت سے سوالات ہیں جن کے جوابات دینے کی ضرورت ہے۔