اعلی تعدد تجارتی حکمت عملی کے بارے میں خیالات (2)
 1
1
 3416
3416
مضمون بنیادی طور پر اعلی تعدد تجارتی حکمت عملیوں پر بحث کرتا ہے، مجموعی حجم کی ماڈلنگ اور قیمت کے جھٹکے پر توجہ مرکوز کرتا ہے۔ یہ مقالہ سنگل لین دین، مقررہ وقفہ قیمت کے جھٹکے، اور قیمتوں پر لین دین کے حجم کے اثرات کا تجزیہ کرتے ہوئے ایک ابتدائی بہترین آرڈر پلیسمنٹ ماڈل تجویز کرتا ہے۔ یہ ماڈل حجم اور قیمت کے جھٹکے کی سمجھ کی بنیاد پر بہترین تجارتی پوزیشن تلاش کرنے کی کوشش کرتا ہے۔ ماڈل کے مفروضوں پر گہرائی سے تبادلہ خیال کیا گیا ہے، اور اصل اور ماڈل کی پیشن گوئی متوقع واپسیوں کا موازنہ کرکے بہترین آرڈر کی جگہ کا ابتدائی جائزہ لیا جاتا ہے۔
مجموعی والیوم ماڈلنگ
پچھلے مضمون نے ایک لین دین کے حجم کے ایک خاص قدر سے زیادہ ہونے کے امکانی اظہار کو اخذ کیا تھا:
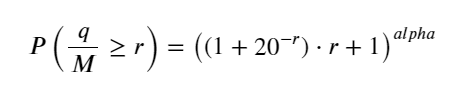
ہم وقت کی ایک مدت میں تجارتی حجم کی تقسیم کے بارے میں بھی فکر مند ہیں، جو کہ ہر لین دین کے حجم اور آرڈر کی فریکوئنسی سے متعلق ہونا چاہیے۔ اگلا، ڈیٹا کو مقررہ وقفوں پر پروسیس کیا جاتا ہے۔ اوپر کی طرح اس کی تقسیم کا منصوبہ بنائیں۔
from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
trades = pd.read_csv('HOOKUSDT-aggTrades-2023-01-27.csv')
trades['date'] = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index = trades['date']
buy_trades = trades[trades['is_buyer_maker']==False].copy()
buy_trades = buy_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
buy_trades['interval']=buy_trades['transact_time'] - buy_trades['transact_time'].shift()
buy_trades.index = buy_trades['date']
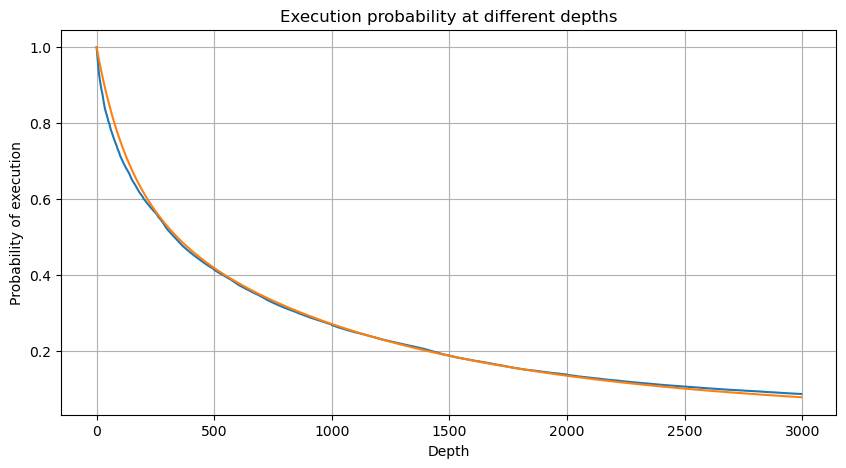
ہر 1s میں لین دین کے حجم کو جوڑ کر، ان حصوں کو ہٹا کر جہاں کوئی لین دین نہیں ہوا، اور اوپر دیے گئے واحد لین دین کی تقسیم کے ساتھ فٹ کر کے، یہ دیکھا جا سکتا ہے کہ اگر 1s کے اندر تمام لین دین کو واحد لین دین کے طور پر شمار کیا جائے تو یہ مسئلہ بہتر ہے۔ یہ ایک حل شدہ مسئلہ بن گیا ہے۔ تاہم، جب سائیکل کو لمبا کیا جاتا ہے (ٹرانزیکشن فریکوئنسی کے نسبت)، خرابی میں اضافہ ہوتا پایا جاتا ہے، اور تحقیق سے پتا چلا ہے کہ یہ غلطی پچھلی Pareto تقسیم کی اصلاح کی اصطلاح کی وجہ سے ہوئی ہے۔ اس کا مطلب یہ ہے کہ جیسے جیسے سائیکل لمبا ہوتا ہے اور اس میں مزید انفرادی لین دین شامل ہوتا ہے، متعدد لین دین کا مجموعہ پیریٹو کی تقسیم تک پہنچ جاتا ہے، اس صورت میں، اصلاح کی اصطلاح کو ہٹا دیا جانا چاہیے۔
df_resampled = buy_trades['quantity'].resample('1S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
buy_trades
| agg_trade_id | price | quantity | first_trade_id | last_trade_id | is_buyer_maker | date | transact_time | interval | diff | |
|---|---|---|---|---|---|---|---|---|---|---|
| 2023-01-27 00:00:00.161 | 1138369 | 2.901 | 54.3 | 3806199 | 3806201 | False | 2023-01-27 00:00:00.161 | 1674777600161 | NaN | 0.001 |
| 2023-01-27 00:00:04.140 | 1138370 | 2.901 | 291.3 | 3806202 | 3806203 | False | 2023-01-27 00:00:04.140 | 1674777604140 | 3979.0 | 0.000 |
| 2023-01-27 00:00:04.339 | 1138373 | 2.902 | 55.1 | 3806205 | 3806207 | False | 2023-01-27 00:00:04.339 | 1674777604339 | 199.0 | 0.001 |
| 2023-01-27 00:00:04.772 | 1138374 | 2.902 | 1032.7 | 3806208 | 3806223 | False | 2023-01-27 00:00:04.772 | 1674777604772 | 433.0 | 0.000 |
| 2023-01-27 00:00:05.562 | 1138375 | 2.901 | 3.5 | 3806224 | 3806224 | False | 2023-01-27 00:00:05.562 | 1674777605562 | 790.0 | 0.000 |
| … | … | … | … | … | … | … | … | … | … | … |
| 2023-01-27 23:59:57.739 | 1544370 | 3.572 | 394.8 | 5074645 | 5074651 | False | 2023-01-27 23:59:57.739 | 1674863997739 | 1224.0 | 0.002 |
| 2023-01-27 23:59:57.902 | 1544372 | 3.573 | 177.6 | 5074652 | 5074655 | False | 2023-01-27 23:59:57.902 | 1674863997902 | 163.0 | 0.001 |
| 2023-01-27 23:59:58.107 | 1544373 | 3.573 | 139.8 | 5074656 | 5074656 | False | 2023-01-27 23:59:58.107 | 1674863998107 | 205.0 | 0.000 |
| 2023-01-27 23:59:58.302 | 1544374 | 3.573 | 60.5 | 5074657 | 5074657 | False | 2023-01-27 23:59:58.302 | 1674863998302 | 195.0 | 0.000 |
| 2023-01-27 23:59:59.894 | 1544376 | 3.571 | 12.1 | 5074662 | 5074664 | False | 2023-01-27 23:59:59.894 | 1674863999894 | 1592.0 | 0.000 |
#1s内的累计分布
depths = np.array(range(0, 3000, 5))
probabilities = np.array([np.mean(df_resampled['quantity'] > depth) for depth in depths])
mean = df_resampled['quantity'].mean()
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([((1+20**(-depth/mean))*depth/mean+1)**(alpha) for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)
df_resampled = buy_trades['quantity'].resample('30S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
depths = np.array(range(0, 12000, 20))
probabilities = np.array([np.mean(df_resampled['quantity'] > depth) for depth in depths])
mean = df_resampled['quantity'].mean()
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([((1+20**(-depth/mean))*depth/mean+1)**(alpha) for depth in depths])
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2)
probabilities_s_2 = np.array([(depth/mean+1)**alpha for depth in depths]) # 无修正
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities,label='Probabilities (True)')
plt.plot(depths, probabilities_s, label='Probabilities (Simulation 1)')
plt.plot(depths, probabilities_s_2, label='Probabilities (Simulation 2)')
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.legend()
plt.grid(True)
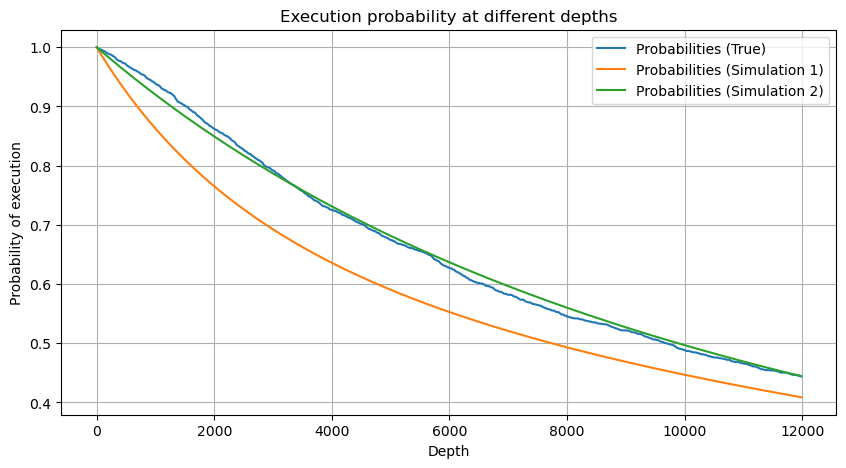
اب ہم نے مختلف اوقات میں جمع شدہ تجارتی حجم کی تقسیم کے لیے ایک عمومی فارمولہ کا خلاصہ کیا ہے، اور ہر بار الگ الگ شمار کیے بغیر، اس میں فٹ ہونے کے لیے واحد لین دین کی تقسیم کا استعمال کیا ہے۔ یہاں ہم عمل کو چھوڑ دیتے ہیں اور براہ راست فارمولا دیتے ہیں:
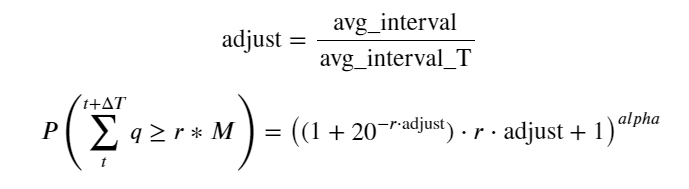
ان میں، avg_interval ایک لین دین کے درمیان اوسط وقفہ کی نمائندگی کرتا ہے، اور avg_interval_T ان وقفوں کے اوسط وقفہ کی نمائندگی کرتا ہے جس کا اندازہ لگانے کی ضرورت ہے۔ اگر ہم 1 سیکنڈ کے لین دین کے وقت کا اندازہ لگانا چاہتے ہیں، تو ہمیں ان واقعات کے درمیان اوسط وقفہ کا حساب لگانا ہوگا جن میں 1 سیکنڈ کے اندر لین دین ہوتا ہے۔ اگر کسی آرڈر کی آمد کا امکان پوسن کی تقسیم سے مطابقت رکھتا ہے، تو یہاں اس کا براہ راست اندازہ لگانا ممکن ہے، لیکن اصل انحراف بڑا ہے، اس لیے میں یہاں اس کی وضاحت نہیں کروں گا۔
نوٹ کریں کہ ایک خاص وقفہ کے اندر حجم کے ایک خاص قدر سے زیادہ ہونے کا امکان گہرائی میں اس پوزیشن پر لین دین کے حقیقی امکان سے بالکل مختلف ہونا چاہیے، کیونکہ انتظار کا وقت جتنا زیادہ ہوگا، آرڈر بک کا امکان اتنا ہی زیادہ ہوگا۔ تبدیل ہوتا ہے، اور لین دین بھی گہرائی میں تبدیلی کی طرف لے جاتا ہے، لہذا اسی گہرائی کی پوزیشن پر لین دین کا امکان حقیقی وقت میں تبدیل ہوتا ہے جیسا کہ ڈیٹا اپ ڈیٹ ہوتا ہے۔
df_resampled = buy_trades['quantity'].resample('2S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
depths = np.array(range(0, 6500, 10))
probabilities = np.array([np.mean(df_resampled['quantity'] > depth) for depth in depths])
mean = buy_trades['quantity'].mean()
adjust = buy_trades['interval'].mean() / 2620
alpha = np.log(np.mean(buy_trades['quantity'] > mean))/0.7178397931503168
probabilities_s = np.array([((1+20**(-depth*adjust/mean))*depth*adjust/mean+1)**(alpha) for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)
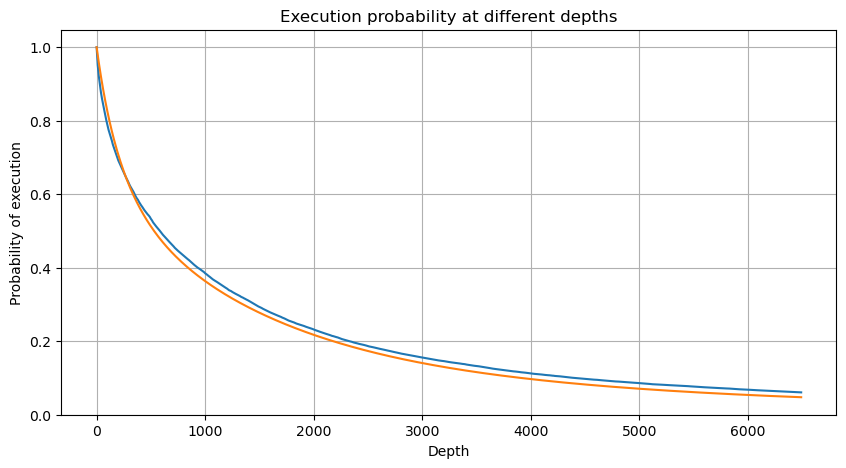
سنگل لین دین کی قیمت کا اثر
لین دین کا ڈیٹا ایک خزانہ ہے، اور ابھی بھی بہت سارے ڈیٹا کو نکالنا باقی ہے۔ ہمیں قیمتوں پر آرڈرز کے اثرات پر پوری توجہ دینی چاہیے، جو حکمت عملی میں زیر التواء آرڈرز کی جگہ کو متاثر کرتی ہے۔ اسی طرح، transact_time کے مجموعی ڈیٹا کی بنیاد پر، آخری قیمت اور پہلی قیمت کے درمیان فرق کا حساب لگائیں اگر صرف ایک آرڈر ہے تو فرق 0 ہے۔ عجیب بات یہ ہے کہ منفی نتائج کے ساتھ اب بھی بہت کم اعداد و شمار موجود ہیں، یہ اعداد و شمار کی ترتیب کے ساتھ ایک مسئلہ ہونا چاہئے، لہذا میں یہاں اس میں نہیں جاؤں گا۔
نتائج سے پتہ چلتا ہے کہ کوئی اثر نہ ہونے کا تناسب 77% تک زیادہ ہے، 1 ٹک کا تناسب 16.5%، 2 ٹک 3.7%، 3 ٹک 1.2%، اور 4 سے زیادہ ٹک کا تناسب 1% سے کم ہے۔ . یہ بنیادی طور پر ایکسپونینشنل فنکشن کی خصوصیات کے مطابق ہے، لیکن فٹنگ درست نہیں ہے۔
لین دین کا حجم جس کی وجہ سے متعلقہ قیمت کا فرق ہوتا ہے کو شمار کیا گیا تھا، اور بہت زیادہ اثر کی وجہ سے ہونے والی تحریف کو ہٹا دیا گیا تھا، یہ بنیادی طور پر لکیری تعلق کے مطابق ہے، اور تقریباً ہر 1,000 والیوم قیمت میں 1 ٹک کے اتار چڑھاؤ کا سبب بنتا ہے۔ یہ بھی سمجھا جا سکتا ہے کہ ہر قیمت کے قریب زیر التواء آرڈرز کی اوسط تعداد تقریباً 1,000 ہے۔
diff_df = trades[trades['is_buyer_maker']==False].groupby('transact_time')['price'].agg(lambda x: abs(round(x.iloc[-1] - x.iloc[0],3)) if len(x) > 1 else 0)
buy_trades['diff'] = buy_trades['transact_time'].map(diff_df)
diff_counts = buy_trades['diff'].value_counts()
diff_counts[diff_counts>10]/diff_counts.sum()
0.000 0.769965
0.001 0.165527
0.002 0.037826
0.003 0.012546
0.004 0.005986
0.005 0.003173
0.006 0.001964
0.007 0.001036
0.008 0.000795
0.009 0.000474
0.010 0.000227
0.011 0.000187
0.012 0.000087
0.013 0.000080
Name: diff, dtype: float64
diff_group = buy_trades.groupby('diff').agg({
'quantity': 'mean',
'diff': 'last',
})
diff_group['quantity'][diff_group['diff']>0][diff_group['diff']<0.01].plot(figsize=(10,5),grid=True);
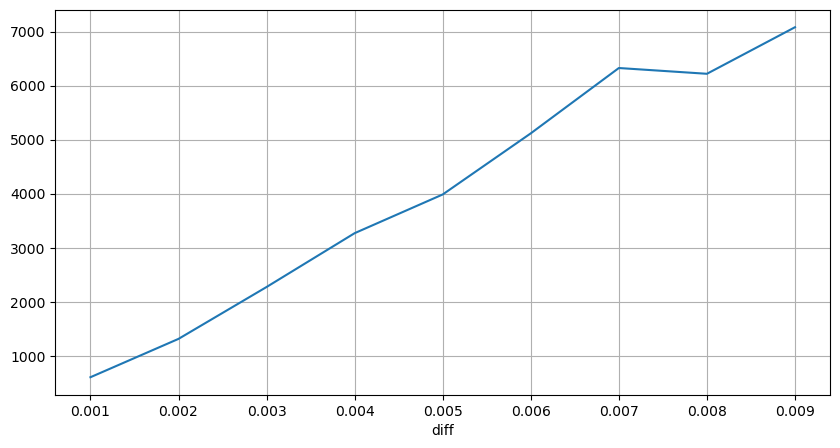
قیمتوں کے جھٹکے باقاعدہ وقفوں سے
2 سیکنڈ کے اندر قیمت کے اثرات کو شمار کریں یہاں پر منفی قدریں ہوں گی، چونکہ یہاں صرف خرید کے آرڈرز شمار کیے جاتے ہیں، اس لیے ہم آہنگ پوزیشن ایک ٹک بڑی ہوگی۔ تجارتی حجم اور اثر کے درمیان تعلق کا مشاہدہ کرنا جاری رکھیں، اور صرف 0 سے زیادہ کے نتائج کو شمار کریں۔ نتیجہ ایک ہی آرڈر سے ملتا جلتا ہے، جو کہ ہر ٹک کے لیے تقریباً 2000 والیوم کی ضرورت ہوتی ہے۔
df_resampled = buy_trades.resample('2S').agg({
'price': ['first', 'last', 'count'],
'quantity': 'sum'
})
df_resampled['price_diff'] = round(df_resampled[('price', 'last')] - df_resampled[('price', 'first')],3)
df_resampled['price_diff'] = df_resampled['price_diff'].fillna(0)
result_df_raw = pd.DataFrame({
'price_diff': df_resampled['price_diff'],
'quantity_sum': df_resampled[('quantity', 'sum')],
'data_count': df_resampled[('price', 'count')]
})
result_df = result_df_raw[result_df_raw['price_diff'] != 0]
result_df['price_diff'][abs(result_df['price_diff'])<0.016].value_counts().sort_index().plot.bar(figsize=(10,5));
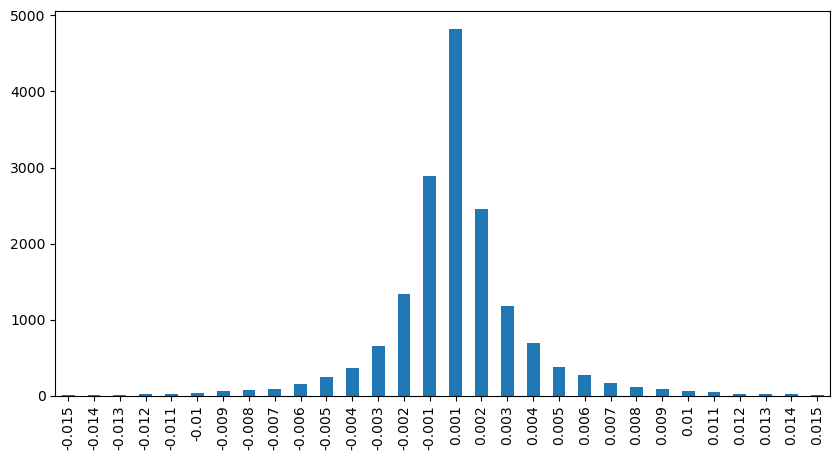
result_df['price_diff'].value_counts()[result_df['price_diff'].value_counts()>30]
0.001 7176
-0.001 3665
0.002 3069
-0.002 1536
0.003 1260
0.004 692
-0.003 608
0.005 391
-0.004 322
0.006 259
-0.005 192
0.007 146
-0.006 112
0.008 82
0.009 75
-0.007 75
-0.008 65
0.010 51
0.011 41
-0.010 31
Name: price_diff, dtype: int64
diff_group = result_df.groupby('price_diff').agg({ 'quantity_sum': 'mean'})
diff_group[(diff_group.index>0) & (diff_group.index<0.015)].plot(figsize=(10,5),grid=True);
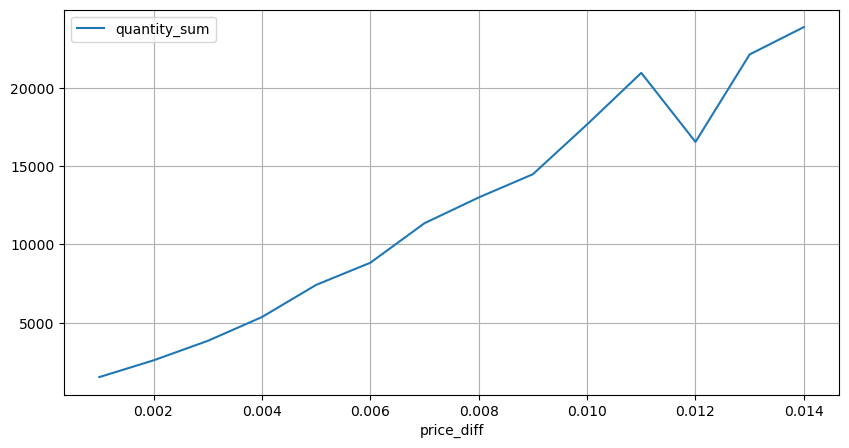
حجم کا قیمت کا اثر
ٹک کی تبدیلی کے لیے مطلوبہ حجم کا حساب پہلے لگایا گیا تھا، لیکن یہ درست نہیں ہے کیونکہ یہ اس مفروضے پر مبنی ہے کہ اثر پہلے ہی واقع ہو چکا ہے۔ اب آئیے تجارتی حجم کی وجہ سے قیمت کے اثرات کو دیکھتے ہیں۔
یہاں ڈیٹا کو 1 سیکنڈ میں نمونہ دیا گیا ہے، جس میں 100 مقداریں ایک قدم کی لمبائی کے طور پر ہیں، اور اس مقدار کی حد کے اندر قیمت کی تبدیلیوں کو شمار کیا جاتا ہے۔ کچھ قیمتی نتائج اخذ کیے گئے:
- جب خرید کا حجم 500 سے نیچے ہوتا ہے تو، متوقع قیمت میں تبدیلی کم ہوتی ہے، جس کی توقع کی جاتی ہے کیونکہ قیمت کو متاثر کرنے والے سیل آرڈرز بھی ہوتے ہیں۔
- جب تجارتی حجم کم ہوتا ہے، تو یہ ایک لکیری تعلق کی پیروی کرتا ہے، یعنی تجارتی حجم جتنا زیادہ ہوگا، قیمت میں اتنا ہی زیادہ اضافہ ہوگا۔
- خرید آرڈر کا حجم جتنا بڑا ہوگا، قیمت میں تبدیلی اتنی ہی زیادہ ہوگی، جو کہ بریک تھرو کے بعد، مقررہ وقفوں پر نمونے لینے کے ساتھ واپس آ سکتی ہے، ڈیٹا غیر مستحکم ہے۔
- سکیٹر پلاٹ کے اوپری حصے پر توجہ دی جانی چاہیے، یعنی وہ حصہ جہاں والیوم قیمت میں اضافے سے مطابقت رکھتا ہے۔
- صرف اس تجارتی جوڑے کے لیے، حجم اور قیمت میں تبدیلی کے درمیان تعلق کا ایک موٹا ورژن دیا گیا ہے:
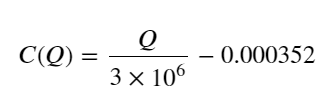
ان میں، “C” قیمت میں تبدیلی کی نمائندگی کرتا ہے اور “Q” خرید آرڈر والیوم کی نمائندگی کرتا ہے۔
df_resampled = buy_trades.resample('1S').agg({
'price': ['first', 'last', 'count'],
'quantity': 'sum'
})
df_resampled['price_diff'] = round(df_resampled[('price', 'last')] - df_resampled[('price', 'first')],3)
df_resampled['price_diff'] = df_resampled['price_diff'].fillna(0)
result_df_raw = pd.DataFrame({
'price_diff': df_resampled['price_diff'],
'quantity_sum': df_resampled[('quantity', 'sum')],
'data_count': df_resampled[('price', 'count')]
})
result_df = result_df_raw[result_df_raw['price_diff'] != 0]
df = result_df.copy()
bins = np.arange(0, 30000, 100) #
labels = [f'{i}-{i+100-1}' for i in bins[:-1]]
df.loc[:, 'quantity_group'] = pd.cut(df['quantity_sum'], bins=bins, labels=labels)
grouped = df.groupby('quantity_group')['price_diff'].mean()
grouped_df = pd.DataFrame(grouped).reset_index()
grouped_df['quantity_group_center'] = grouped_df['quantity_group'].apply(lambda x: (float(x.split('-')[0]) + float(x.split('-')[1])) / 2)
plt.figure(figsize=(10,5))
plt.scatter(grouped_df['quantity_group_center'], grouped_df['price_diff'],s=10)
plt.plot(grouped_df['quantity_group_center'], np.array(grouped_df['quantity_group_center'].values)/2e6-0.000352,color='red')
plt.xlabel('quantity_group_center')
plt.ylabel('average price_diff')
plt.title('Scatter plot of average price_diff by quantity_group')
plt.grid(True)
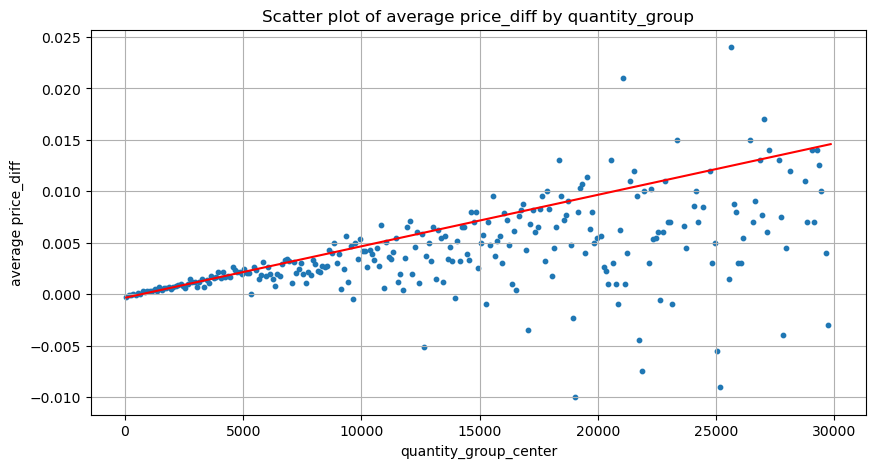
grouped_df.head(10)
| quantity_group | price_diff | quantity_group_center | |
|---|---|---|---|
| 0 | 0-199 | -0.000302 | 99.5 |
| 1 | 100-299 | -0.000124 | 199.5 |
| 2 | 200-399 | -0.000068 | 299.5 |
| 3 | 300-499 | -0.000017 | 399.5 |
| 4 | 400-599 | -0.000048 | 499.5 |
| 5 | 500-699 | 0.000098 | 599.5 |
| 6 | 600-799 | 0.000006 | 699.5 |
| 7 | 700-899 | 0.000261 | 799.5 |
| 8 | 800-999 | 0.000186 | 899.5 |
| 9 | 900-1099 | 0.000299 | 999.5 |
ابتدائی بہترین آرڈر کی پوزیشن
تجارتی حجم کی ماڈلنگ اور قیمت کے اثرات سے مطابقت رکھنے والے تجارتی حجم کے ایک کھردرے ماڈل کے ساتھ، ایسا لگتا ہے کہ آرڈر کی بہترین پوزیشن کا حساب لگایا جا سکتا ہے۔ آئیے کچھ مفروضے بناتے ہیں اور ایک غیر ذمہ دارانہ بہترین قیمت کی پوزیشن دیتے ہیں۔
- فرض کریں کہ جھٹکے کے بعد قیمت اپنی اصل قیمت پر واپس آجاتی ہے (یقیناً اس کا امکان نہیں ہے اور جھٹکے کے بعد قیمت میں تبدیلی کے دوبارہ تجزیہ کی ضرورت ہے)
- فرض کریں کہ اس مدت کے دوران تجارتی حجم اور آرڈر کی فریکوئنسی کی تقسیم پہلے سے طے شدہ تقاضوں کو پورا کرتی ہے (یہ بھی غلط ہے، کیونکہ ایک دن کی قدر تخمینہ کے لیے استعمال ہوتی ہے، اور لین دین میں واضح کلسٹرنگ ہوتی ہے)۔
- فرض کریں کہ نقلی وقت کے دوران صرف ایک سیل آرڈر ہوتا ہے اور پھر پوزیشن بند ہوجاتی ہے۔
- یہ فرض کرتے ہوئے کہ آرڈر پر عمل درآمد کے بعد، قیمت کو بڑھانے کے لیے دیگر خرید آرڈرز ہوتے ہیں، خاص طور پر جب اس کا حجم بہت کم ہوتا ہے اور یہ صرف یہ سمجھا جاتا ہے کہ یہ واپس آجائے گا۔
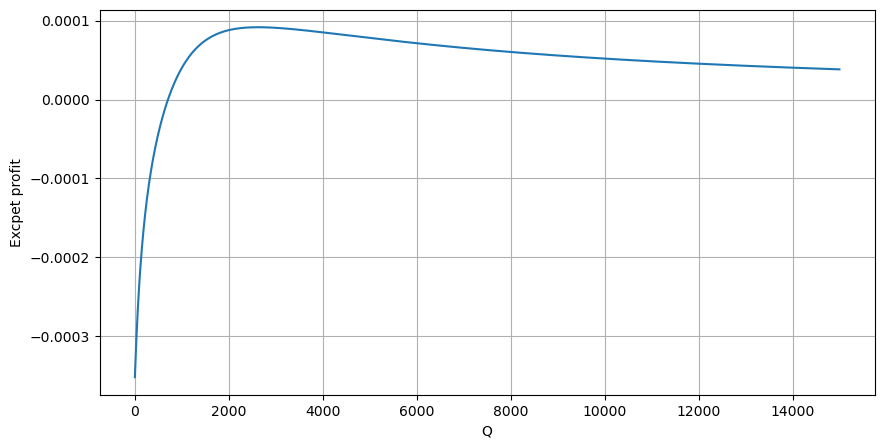
سب سے پہلے، ایک سادہ متوقع واپسی لکھیں، یعنی یہ امکان کہ مجموعی خرید آرڈر 1 سیکنڈ کے اندر Q سے زیادہ ہے، واپسی کی متوقع شرح (یعنی اثر کی قیمت) سے ضرب:
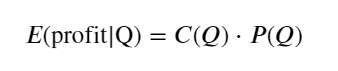
گراف کے مطابق، متوقع واپسی زیادہ سے زیادہ 2500 کے قریب ہے، جو کہ اوسط تجارتی حجم کا تقریباً 2.5 گنا ہے۔ یعنی فروخت کا آرڈر 2500 پر دیا جائے۔ اس پر دوبارہ زور دینے کی ضرورت ہے کہ افقی محور 1 سیکنڈ کے اندر تجارتی حجم کی نمائندگی کرتا ہے اور اسے محض گہرائی کی پوزیشن سے ہم آہنگ نہیں کیا جا سکتا۔ اور یہ ایک ایسے وقت میں ہے جب ابھی بھی بہت اہم گہرائی والے ڈیٹا کی کمی ہے، اور یہ صرف قیاس آرائیوں پر مبنی تجارت پر مبنی ہے۔
خلاصہ کریں۔
یہ پایا گیا ہے کہ مختلف وقت کے وقفوں پر حجم کی تقسیم کسی ایک لین دین کے حجم کی تقسیم کا ایک سادہ پیمانہ ہے۔ ہم نے قیمتوں کے جھٹکے اور لین دین کے امکانات کی بنیاد پر ایک سادہ متوقع ریٹرن ماڈل بنایا ہے اگر فروخت آرڈر کا حجم کم ہے تو اس سے قیمت میں کمی کی ضرورت ہے۔ منافع کا مارجن ہے، اور لین دین کا حجم جتنا زیادہ ہوگا، اس کا امکان اتنا ہی کم ہوگا، جو کہ آرڈر پلیسمنٹ کی پوزیشن ہے جس کی حکمت عملی تلاش کر رہی ہے۔ بلاشبہ، یہ ماڈل اب بھی بہت آسان ہے، میں اس پر گہرائی سے بات کرتا رہوں گا۔
#1s内的累计分布
df_resampled = buy_trades['quantity'].resample('1S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
depths = np.array(range(0, 15000, 10))
mean = df_resampled['quantity'].mean()
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([((1+20**(-depth/mean))*depth/mean+1)**(alpha) for depth in depths])
profit_s = np.array([depth/2e6-0.000352 for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities_s*profit_s)
plt.xlabel('Q')
plt.ylabel('Excpet profit')
plt.grid(True)