基于机器学习的订单簿高频交易策略

基于机器学习的订单簿高频交易策略

• ### 一、绪论 证券市场的交易机制可以分为报价驱动市场和订单驱动市场两类，前者依赖做市商提供流动性，后者是通过限价单提供流动性，交易通过投资者的买进委托和卖出委托竞价所形成。中国的证券市场属于订单驱动市场，包括股票市场和期货市场。

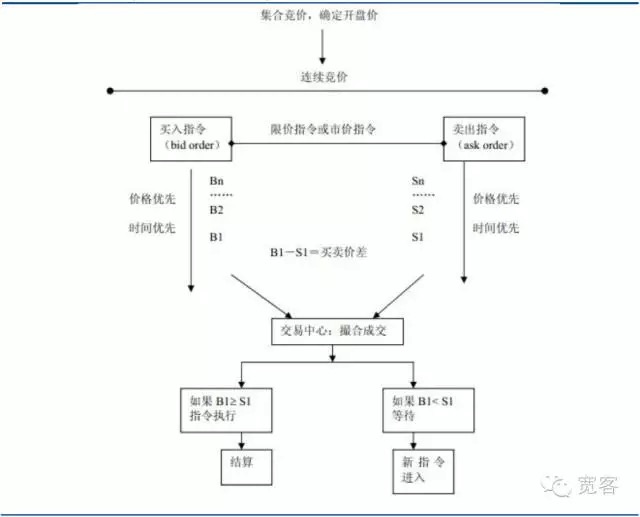图1 订单驱动市场示意图

• （一）限价单订单簿简介

  订单簿的研究属于市场微观结构研究范畴，市场微观结构理论以微观经济学中的价格理论和厂商理论作为其思想渊源，而在对其核心问题——金融资产交易及其价格形成过程和原因的分析中，则用到了一般均衡、局部均衡、边际收益、边际成本、市场连续性、存货理论、博弈论、信息经济学等多种理论与方法。

  从国外的研究进展来看，市场微观结构领域以O’Hara为代表，大部分理论都是基于做市商市场（也就是报价驱动市场），例如存货模型和信息模型等。今年来，实际的交易市场中，订单驱动已经逐步占据上方，但专门针对订单驱动市场的研究还比较少。

  国内证券市场和期货市场都属于订单驱动市场，下图是股指期货合约IF1312的Level_1行情订单簿截图。从上面直接获得的信息并不多，基础信息就包括买一价、卖一价、买一量和卖一量。在国外的某些学术论文中，和订单簿对应的还有信息簿，包括最明细的订单撮合数据，包括每个订单的下单量、成交价、订单类型等信息，由于国内市场不公开信息簿的信息，因此超高频交易我们只能依赖订单簿。

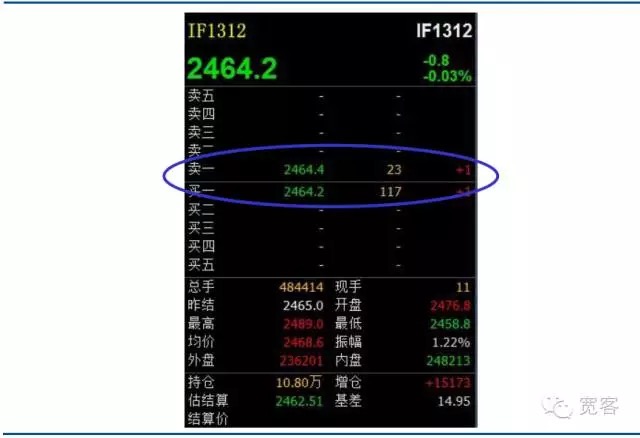  图2 股指期货主力合约Level-1订单簿

• （二）订单簿高频交易研究进展

  订单簿的动态建模，主要有两种方法，一种是经典计量经济学方法，另一种是机器学习方法。 计量经济学方法是一种经典的主流研究方法，例如研究价差分析的MRR分解、Huang和Stoll分解等， 研究订单持续期的ACD模型，研究价格预测的Logistic模型。

  机器学习在金融领域的学术研究也非常活跃，比如2012年的《Forecasting trends of high_frequency KOSPI200 index data using learning classifiers》是一种常见研究思路，利用技术分析常见的指标（MA、EMA、RSI等），引入机器学习的分类方法进行市场预测。但这种做法对订单簿动态信息挖掘不足，也就是说，利用订单簿动态信息进行高抛交易的研究在国内外都还比较少，这是很值得深入研究的领域。

• 二、机器学习在订单簿高频交易中的应用

  • #### (一)系统架构图 下图是典型的机器学习交易策略的系统架构图，包括订单簿数据、特征发现、模型构建与验证和交易机会几个主要模块，值得注意的是，交易过程是由行情事件触发的，tick行情的到达是其中一个事件。

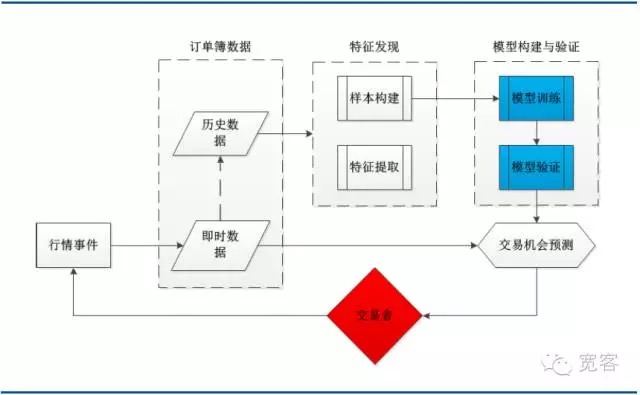  图3 基于机器学习的订单簿建模的系统架构图

  • #### (二)支持向量机简介 20世纪70年代，Vapnik等人开始建立起一套比较完善的理论体系——统计学习理论(SLT, Statistical Learning Theory)，它用于研究有限样本情形下统计规律和学习方法性质，为有限样本的机器学习问题建立了一个良好的理论框架，较好地解决了小样本、非线性、高维数和局部极小点等实际问题。1995年，Vapnik等人明确提出一种新的通用学习方法——支持向量机(SVM, Support Vector Machine)后，该理论受到广泛的重视并应用到不同的领域，它已初步表现出很多优于己有方法的性能。

  SVM 是从线性可分情况下的最优分类超平面发展而来的。对两类分类问题,设训练样本集为(xi,yi),i=1,2…l，l为训练样本的个数,xi为训练样本, yi属于{-1,+1}是输入样本xi的类标记(期望输出) 。SVM 算法的出发点是寻找最优分类超平面。

  最优分类超平面不但能将所有样本正确分开(训练错分率为0) ,而且能够使两类间的边际(margin)最大,边际定义为训练数据集到该分类超平面的最小距离之和。最优分类超平面意味着对测试数据平均分类误差最小。

  如果存在d维矢量空间中的一个超平面：

  F(x)=w*x+b=0

  能够将上述两类数据分开，则称该超平面为分界面。这里w*x为d维矢量空间中两个矢量w和x的内积。

  如果分界面：

  w*x+b=0

  能使到该分界面最近的两类样本之间的距离(Margin)最大，就称该分界面为最优分界面。

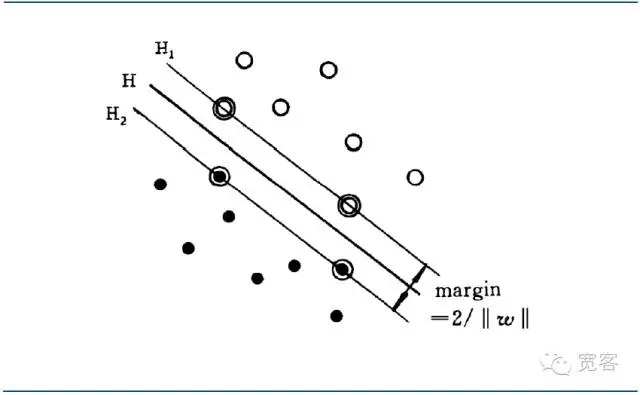  图4 SVM二分类最优分界面示意图

  对最优分界面方程进行归一化，可以使得两类样本之间的距离

  

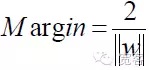
  于是对于任意一个样本，都有

  

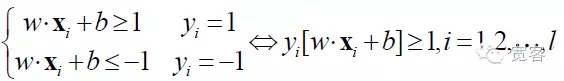
  要得到最优分界面，除了满足上面的式外，还要最小化。

  从而SVM问题的数学模型为：

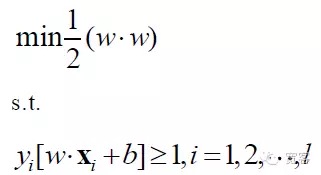
  SVM最终变成一个最优化的规划问题，学术界的研究热点主要集中快速求解、推广到多分类、实际问题应用等。

  SVM最初是针对二分类问题提出的，根据目前的实际应用要求，将其推广到多分类问题。已有的多分类算法包括一对多、一对一、纠错编码、DAG-SVM 和Mult i-class SVM分类器等。

  • #### (三)订单簿指标提取 以股指期货Level-1行情为例，订单簿主要包括买一价、卖一价、买一量、卖一量等基础指标，并可以衍生出深度、斜率、相对价差等指标，其他指标包括持仓量、成交量、基差等 ，共计17个指标，如下表所示。 还可以引入常见的技术分析指标如RSI、KDJ、MA、EMA等。

  表1 基于Level行情订单簿的指标库

  

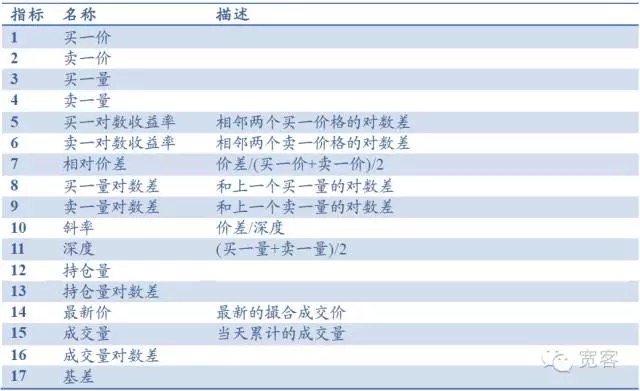
  • #### (四)订单簿的动量特征刻画和交易机会 在市场微观角度，有两种衡量短时间内价格动量的方法，一种是中间价动量，另一种是价差交叉。本文选择更加简单直观的中间价动量。中间价的定义：

  

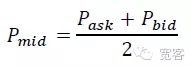
  根据订单簿在Δt内的中间价ΔP变化大小分为“涨”“跌平”三个类别。

  下图是主力合约IF1311在10月29日的中间价动量分布，每天有32400个tick行情数据。

  在Δt=1tick的情况下，中间价变化绝对值0.2大约有6000次，变化绝对值为0.4大约有 1500次，变化绝对值为0.6大约有150次，变化绝对值为0.8大于有50次，变化绝对值大于等于1大约有10次。

  在Δt=2tick的情况下，中间价变化绝对值0.2大约有7000次，变化绝对值为0.4大约有3000次，变化绝对值为0.6大约有550次，变化绝对值为0.8大约有205次，变化绝对值大于等于1大约有10次。

  我们认为，变化绝对值大于等于0.4的情况下，是潜在交易机会。在Δt=1tick情况下，每天大约有1700次机会；Δt=2tick情况下，每天大约有4000次机会。

  

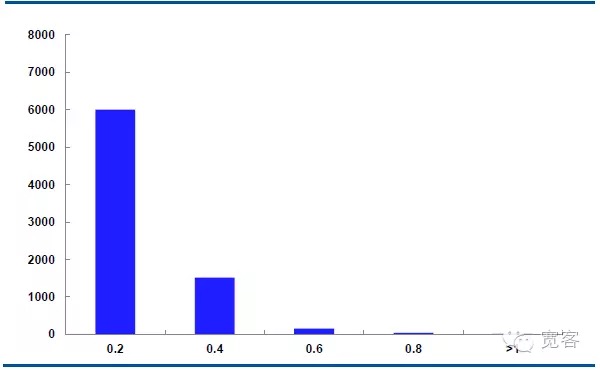
  图5 IF1311在10月29日中间价变化分布图(Δt=1tick)

  

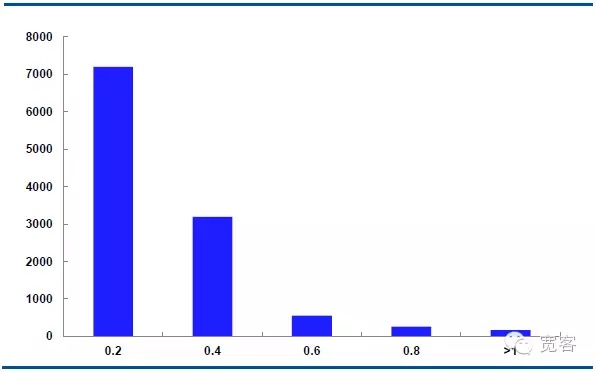
  图6 IF1311在10月29日中间价变化分布图(Δt=2tick)

• 三、策略实证

  由于SVM模型在大样本情况下的训练复杂度比较高，训练时间较长，我们选择的历史行情数据跨期相对比较短，以IF1311合约在10月的Level_1行情数据为例，验证模型的有效性。

  • #### (一)模型效果检验 数据周期：IF1311合约在10月份的行情数据；

  Δt取值：Δt越小，对交易细节要求越高，当Δt=1tick时，实际交易中很难获得收益，为了对比模型的效果，这里分别取值1tick、2tick、3tick；

  模型评价指标：样本准确率、检验准确率、预测时间。 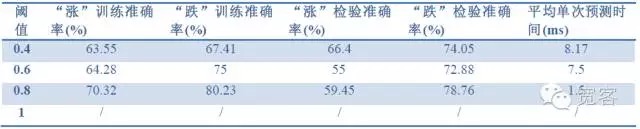表2 以1tick数据预测1tick的效果

  表3 以1tick数据预测tick2的效果

  表4 以2tick数据预测2tick的效果

  从上面三个表格的数据，我们可以得到下一些结论： 最高准确率大概达到70%，在准确率达到60%，可以转化为交易策略。

  • #### (二)策略模拟收益 以10月31日为例，我们进行模拟交易，机构的股指期货交易手续费一般是机构的股指期货交易手续费一般是0.²⁶⁄₁₀₀₀₀, 我们假设交易次数不收所限制，假设每次交易单边滑价为0.2点，每次下单手数为1手。

  表5 模拟策略在10月31日的交易情况

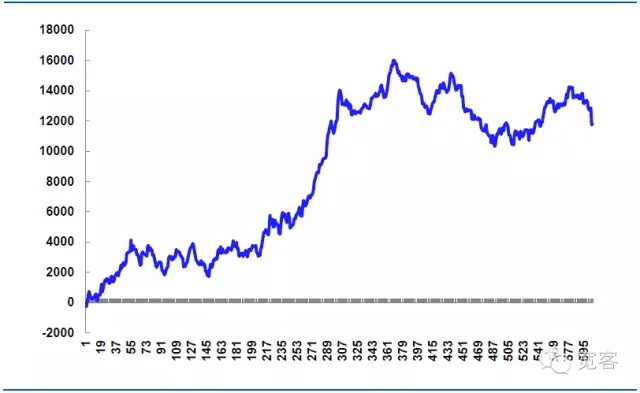
  全天交易次数605次，包含手续情况下，盈利次数339次，胜率56%，净利润11814.99元。

  理论上的滑价是14520元，这部分是策略实战的关键，如果下单细节控制得更加精细，那么可以减少滑价，提高净利润，如果下单细节控制不当，或者市场波动异常，滑价会更大，而净利润会减少，因此高频交易的成败往往取决于细节的执行。

  图7 模拟策略在10月31日的收益

原创声明：本文系宽客公众号作者原创，转载请注明出处。