Modellierung und Analyse der Volatilität von Bitcoin auf Basis des ARMA-EGARCH-Modells

Vor kurzem habe ich einige Analysen über die Volatilität von Bitcoin gemacht, die wortreich und spontan ist. Also teile ich einfach einige meiner Verständnisse und Code wie folgt. Meine Fähigkeit ist begrenzt, und der Code ist nicht sehr perfekt. Wenn es irgendeinen Fehler gibt, bitte weisen Sie darauf hin und korrigieren Sie ihn direkt.

1. Eine kurze Beschreibung der Zeitreihen der Finanzmärkte

Die Zeitreihe der Finanzen ist ein Satz von Stochastischen Prozessreihe-Modellen, die auf einer Variablen basieren, die in der Zeitdimension beobachtet wird. Die Variable ist in der Regel die Rendite von Vermögenswerten. Da die Rendite unabhängig von der Investitionsskala ist und eine statistische Natur hat, ist es wertvoller, die Investitionsmöglichkeiten der zugrunde liegenden finanziellen Vermögenswerte zu analysieren.

Hier wird kühn davon ausgegangen, dass die Rendite von Bitcoin den Renditenmerkmalen allgemeiner Finanzanlagen entspricht, d. h. es handelt sich um eine schwach glatte Reihe, die durch Konsistenzprüfung mehrerer Proben nachgewiesen werden kann.

1-1. Vorbereitungen, Importbibliotheken, Verkapselungsfunktionen

Die Konfiguration der Forschungsumgebung ist abgeschlossen. Die für nachfolgende Berechnungen erforderliche Bibliothek wird hier importiert. Da sie intermittierend geschrieben wird, kann sie überflüssig sein. Bitte bereinigen Sie sie selbst.

In [1]:

'''
start: 2020-02-01 00:00:00
end: 2020-03-01 00:00:00
period: 1h
exchanges: [{"eid":"Huobi","currency":"BTC_USDT","stocks":0}]
'''
from __future__ import absolute_import, division, print_function
from fmz import * # Import all FMZ functions
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.lines as mlines
import seaborn as sns
import statsmodels.api as sm
import statsmodels.formula.api as smf
import statsmodels.tsa.api as smt
from statsmodels.graphics.api import qqplot
from statsmodels.stats.diagnostic import acorr_ljungbox as lb_test
from scipy import stats
from arch import arch_model
from datetime import timedelta
from itertools import product
from math import sqrt
from sklearn.metrics import r2_score, mean_absolute_error, mean_squared_error

task = VCtx(__doc__) # Initialization, verification of FMZ reading of historical data
print(exchange.GetAccount())

Ausgeschaltet[1]: {Bilanz: 10000.0, FrozenBalance: 0.0, Beständen: 0.0, FrozenBeständen: 0.0}

    #### Encapsulate some of the functions, which will be used later. If there is a source, see the note

In [17]:

# Plot functions
def tsplot(y, y_2, lags=None, title='', figsize=(18, 8)):  # source code: https://tomaugspurger.github.io/modern-7-timeseries.html
    fig = plt.figure(figsize=figsize)
    layout = (2, 2)
    ts_ax   = plt.subplot2grid(layout, (0, 0))
    ts2_ax = plt.subplot2grid(layout, (0, 1))
    acf_ax  = plt.subplot2grid(layout, (1, 0))
    pacf_ax = plt.subplot2grid(layout, (1, 1))
    y.plot(ax=ts_ax)
    ts_ax.set_title(title)
    y_2.plot(ax=ts2_ax)
    smt.graphics.plot_acf(y, lags=lags, ax=acf_ax)
    smt.graphics.plot_pacf(y, lags=lags, ax=pacf_ax)
    [ax.set_xlim(0) for ax in [acf_ax, pacf_ax]]
    sns.despine()
    plt.tight_layout()
    return ts_ax, ts2_ax, acf_ax, pacf_ax

# Performance evaluation
def get_rmse(y, y_hat):
    mse = np.mean((y - y_hat)**2)
    return np.sqrt(mse)

def get_mape(y, y_hat):
    perc_err = (100*(y - y_hat))/y
    return np.mean(abs(perc_err))

def get_mase(y, y_hat):
    abs_err = abs(y - y_hat)
    dsum=sum(abs(y[1:] - y_hat[1:]))
    t = len(y)
    denom = (1/(t - 1))* dsum
    return np.mean(abs_err/denom)

def mae(observation, forecast):    
    error = mean_absolute_error(observation, forecast)
    print('Mean Absolute Error (MAE): {:.3g}'.format(error))
    return error

def mape(observation, forecast): 
    observation, forecast = np.array(observation), np.array(forecast)
    # Might encounter division by zero error when observation is zero
    error = np.mean(np.abs((observation - forecast) / observation)) * 100
    print('Mean Absolute Percentage Error (MAPE): {:.3g}'.format(error))
    return error

def rmse(observation, forecast):
    error = sqrt(mean_squared_error(observation, forecast))
    print('Root Mean Square Error (RMSE): {:.3g}'.format(error))
    return error

def evaluate(pd_dataframe, observation, forecast):
    first_valid_date = pd_dataframe[forecast].first_valid_index()
    mae_error = mae(pd_dataframe[observation].loc[first_valid_date:, ], pd_dataframe[forecast].loc[first_valid_date:, ])
    mape_error = mape(pd_dataframe[observation].loc[first_valid_date:, ], pd_dataframe[forecast].loc[first_valid_date:, ])
    rmse_error = rmse(pd_dataframe[observation].loc[first_valid_date:, ], pd_dataframe[forecast].loc[first_valid_date:, ]) 

    ax = pd_dataframe.loc[:, [observation, forecast]].plot(figsize=(18,5))
    ax.xaxis.label.set_visible(False)
    return

Lassen Sie uns mit einem kurzen Verständnis der historischen Daten von Bitcoin beginnen

Aus statistischer Sicht können wir uns einige Datenmerkmale von Bitcoin ansehen. Unter Berücksichtigung der Datenbeschreibung des vergangenen Jahres als Beispiel wird die Rendite auf einfache Weise berechnet, dh der Schlusskurs wird logarithmisch subtrahiert. Die Formel lautet wie folgt: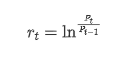

In [3]:

df = get_bars('huobi.btc_usdt', '1d', count=10000, start='2019-01-01')
btc_year = pd.DataFrame(df['close'],dtype=np.float)
btc_year.index.name = 'date'
btc_year.index = pd.to_datetime(btc_year.index)
btc_year['log_price'] = np.log(btc_year['close'])
btc_year['log_return'] = btc_year['log_price'] - btc_year['log_price'].shift(1)
btc_year['log_return_100x'] = np.multiply(btc_year['log_return'], 100)

btc_year_test = pd.DataFrame(btc_year['log_return'].dropna(), dtype=np.float)
btc_year_test.index.name = 'date'
mean = btc_year_test.mean()
std = btc_year_test.std()
normal_result = pd.DataFrame(index=['Mean Value', 'Std Value', 'Skewness Value','Kurtosis Value'], columns=['model value'])
normal_result['model value']['Mean Value'] = ('%.4f'% mean[0])
normal_result['model value']['Std Value'] = ('%.4f'% std[0])
normal_result['model value']['Skewness Value'] = ('%.4f'% btc_year_test.skew())
normal_result['model value']['Kurtosis Value'] = ('%.4f'% btc_year_test.kurt())
normal_result

Ausgeschaltet[3]: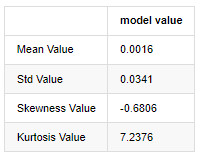

Das Merkmal von dicken Fettschwänzen ist, dass je kürzer die Zeitskala ist, desto signifikanter das Merkmal ist. Die Kurtose wird mit der Zunahme der Datenfrequenz zunehmen, und das Merkmal wird in Hochfrequenzdaten sehr offensichtlich sein.

Nehmen wir die täglichen Schlusskursdaten vom 1. Januar 2019 bis heute als Beispiel, machen wir eine beschreibende Analyse seiner logarithmischen Rendite, und es kann gesehen werden, dass die einfache Rendite-Serie von Bitcoin nicht der normalen Verteilung entspricht und die offensichtliche Eigenschaft von dicken Fettschwänzen aufweist.

Der Durchschnittswert der Sequenz beträgt 0,0016, die Standardabweichung 0,0341, die Verzerrung -0,6819 und die Kurtosis 7,2243, was viel höher ist als die normale Verteilung und die Eigenschaft dicker Fettschwänze aufweist.

In [4]:

fig = plt.figure(figsize=(4,4))
ax = fig.add_subplot(111)
fig = qqplot(btc_year_test['log_return'], line='q', ax=ax, fit=True)

Ausgeschaltet[4]:

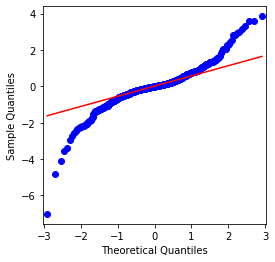
Es kann gesehen werden, dass das QQ-Chart perfekt ist, und die logarithmische Rückkehrreihe für Bitcoin entspricht nicht einer normalen Verteilung aus den Ergebnissen, und es hat offensichtliche Eigenschaft von dicken Fettschwänzen.

Als nächstes betrachten wir den Aggregationseffekt der Volatilität, d. h. Finanzzeitreihen sind oftmals von einer höheren Volatilität nach einer höheren Volatilität begleitet, während nach einer geringeren Volatilität in der Regel eine geringere Volatilität folgt.

Volatilitätsclustering spiegelt die positiven und negativen Rückkopplungseffekte der Volatilität wider und korreliert stark mit den Eigenschaften von Fat Tails. Ökonometrisch bedeutet dies, dass die Zeitreihen der Volatilität autocorrelierbar sind, d.h. die Volatilität der aktuellen Periode kann eine gewisse Beziehung zur vorherigen Periode, zur zweiten vorherigen Periode oder sogar zur dritten vorherigen Periode haben.

In [5]:

df = get_bars('huobi.btc_usdt', '1d', count=50000, start='2006-01-01')
btc_year = pd.DataFrame(df['close'],dtype=np.float)
btc_year.index.name = 'date'
btc_year.index = pd.to_datetime(btc_year.index)
btc_year['log_price'] = np.log(btc_year['close'])
btc_year['log_return'] = btc_year['log_price'] - btc_year['log_price'].shift(1)
btc_year['log_return_100x'] = np.multiply(btc_year['log_return'], 100)

btc_year_test = pd.DataFrame(btc_year['log_return'].dropna(), dtype=np.float)
btc_year_test.index.name = 'date'
sns.mpl.rcParams['figure.figsize'] = (18, 4)  # Volatility
ax1 = btc_year_test['log_return'].plot()
ax1.xaxis.label.set_visible(False)

Ausgeschaltet[5]:

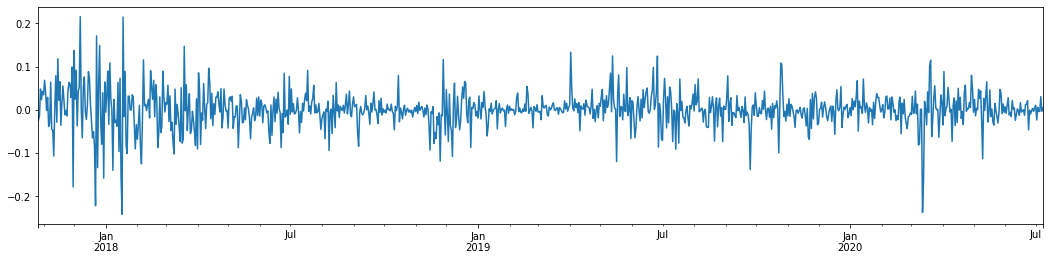
Wenn wir die tägliche logarithmische Rendite von Bitcoin in den letzten 3 Jahren nehmen und sie zeichnen, kann das Phänomen der Volatilitätsclustering deutlich gesehen werden. Nach dem Bullenmarkt in Bitcoin im Jahr 2018 war er die meiste Zeit in einer stabilen Position. Wie wir am rechten Ende sehen können, gab es im März 2020, als die globalen Finanzmärkte stürzten, auch einen Lauf auf die Liquidität von Bitcoin, wobei die Renditen an einem Tag um fast 40% sanken, mit scharfen negativen Schwankungen.

Kurz gesagt, aus der intuitiven Beobachtung können wir sehen, dass eine große Schwankung von einer dichten Schwankung mit großer Wahrscheinlichkeit gefolgt wird, die auch der Aggregateffekt der Volatilität ist. Wenn diese Volatilitätsspanne vorhersehbar ist, ist sie für BTCs kurzfristige Transaktionen wertvoll, was auch der Zweck der Diskussion über Volatilität ist.

1-3. Datenvorbereitung

Um den Trainingsmustersatz vorzubereiten, erstellen wir zunächst eine Benchmark-Stichprobe, in der die logarithmische Rendite die gleichwertige beobachtete Volatilität ist. Da die Volatilität des Tages nicht direkt beobachtet werden kann, werden stündliche Daten für die Neubauung verwendet, um die realisierte Volatilität des Tages abzuleiten und als abhängige Variable der Volatilität zu nehmen.

Die Methode der erneuten Probenahme basiert auf den stündlichen Daten und zeigt folgende Formel: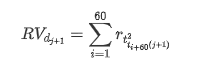

In [4]:

count_num = 100000
start_date = '2020-03-01'

df = get_bars('huobi.btc_usdt', '1m', count=50000, start='2020-02-13')  # Take the minute data
kline_1m = pd.DataFrame(df['close'], dtype=np.float)
kline_1m.index.name = 'date'
kline_1m['log_price'] = np.log(kline_1m['close'])
kline_1m['return'] = kline_1m['close'].pct_change().dropna()
kline_1m['log_return'] = kline_1m['log_price'] - kline_1m['log_price'].shift(1)

kline_1m['squared_log_return'] = np.power(kline_1m['log_return'], 2)

kline_1m['return_100x'] = np.multiply(kline_1m['return'], 100)
kline_1m['log_return_100x'] = np.multiply(kline_1m['log_return'], 100)  # Enlarge 100 times

df = get_bars('huobi.btc_usdt', '1h', count=860, start='2020-02-13')  # Take the hour data
kline_all = pd.DataFrame(df['close'], dtype=np.float)
kline_all.index.name = 'date'
kline_all['log_price'] = np.log(kline_all['close'])  # Calculate daily logarithmic rate of return
kline_all['return'] = kline_all['log_price'].pct_change().dropna()
kline_all['log_return'] = kline_all['log_price'] - kline_all['log_price'].shift(1)  # Calculate logarithmic rate of return
kline_all['squared_log_return'] = np.power(kline_all['log_return'], 2)  # The exponential square of logarithmic daily rate of return

kline_all['return_100x'] = np.multiply(kline_all['return'], 100)
kline_all['log_return_100x'] = np.multiply(kline_all['log_return'], 100)  # Enlarge 100 times

kline_all['realized_variance_1_hour'] = kline_1m.loc[:, 'squared_log_return'].resample('h', closed='left', label='left').sum().copy()  # Resampling to days
kline_all['realized_volatility_1_hour'] = np.sqrt(kline_all['realized_variance_1_hour'])  # Volatility of variance derivation

kline_all = kline_all[4:-29] # Remove the last line because it is missing
kline_all.head(3)

Ausgeschaltet[4]: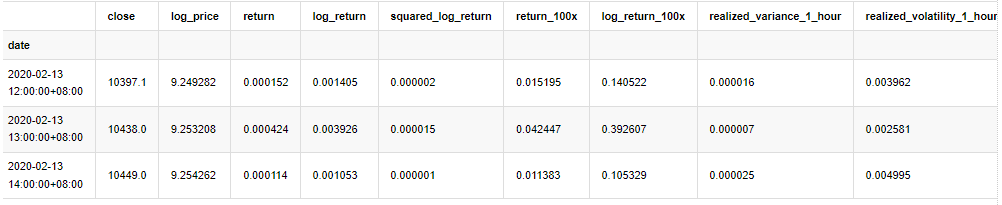

Die Daten außerhalb der Stichprobe werden auf die gleiche Weise vorbereitet

In [5]:

# Prepare the data outside the sample with realized daily volatility
df = get_bars('huobi.btc_usdt', '1m', count=50000, start='2020-02-13')  # Take the minute data
kline_1m = pd.DataFrame(df['close'], dtype=np.float)
kline_1m.index.name = 'date'
kline_1m['log_price'] = np.log(kline_1m['close'])
kline_1m['log_return'] = kline_1m['log_price'] - kline_1m['log_price'].shift(1)
kline_1m['log_return_100x'] = np.multiply(kline_1m['log_return'], 100)  # Enlarge 100 times
kline_1m['squared_log_return'] = np.power(kline_1m['log_return_100x'], 2)
kline_1m#.tail()
df = get_bars('huobi.btc_usdt', '1h', count=860, start='2020-02-13')  # Take the hour data
kline_test = pd.DataFrame(df['close'], dtype=np.float)
kline_test.index.name = 'date'
kline_test['log_price'] = np.log(kline_test['close'])  # Calculate daily logarithmic rate of return
kline_test['log_return'] = kline_test['log_price'] - kline_test['log_price'].shift(1)  # Calculate logarithmic rate of return
kline_test['log_return_100x'] = np.multiply(kline_test['log_return'], 100)  # Enlarge 100 times
kline_test['squared_log_return'] = np.power(kline_test['log_return_100x'], 2)  # The exponential square of logarithmic daily rate of return
kline_test['realized_variance_1_hour'] = kline_1m.loc[:, 'squared_log_return'].resample('h', closed='left', label='left').sum()  # Resampling to days
kline_test['realized_volatility_1_hour'] = np.sqrt(kline_test['realized_variance_1_hour'])  # Volatility of variance derivation
kline_test = kline_test[4:-2]

Um die Grunddaten der Stichprobe zu verstehen, wird eine einfache beschreibende Analyse wie folgt durchgeführt:

In [9]:

line_test = pd.DataFrame(kline_train['log_return'].dropna(), dtype=np.float)
line_test.index.name = 'date'

mean = line_test.mean()  # Calculate mean value and standard deviation
std = line_test.std()

line_test.sort_values(by = 'log_return', inplace = True)  # Resort
s_r = line_test.reset_index(drop = False)  # After resorting, update index
s_r['p'] = (s_r.index - 0.5) / len(s_r)  # Calculate the percentile p(i)
s_r['q'] = (s_r['log_return'] - mean) / std  # Calculate the value of q

st = line_test.describe()
x1 ,y1 = 0.25, st['log_return']['25%']
x2 ,y2 = 0.75, st['log_return']['75%']

fig = plt.figure(figsize = (18,8))
layout = (2, 2)
ax1 = plt.subplot2grid(layout, (0, 0), colspan=2)# Plot the data distribution
ax2 = plt.subplot2grid(layout, (1, 0))# Plot histogram
ax3 = plt.subplot2grid(layout, (1, 1))# Draw the QQ chart, the straight line is the connection of the quarter digit, three-quarters digit, which is basically conforms to the normal distribution

ax1.scatter(line_test.index, line_test.values)
line_test.hist(bins=30,alpha = 0.5,ax = ax2)
line_test.plot(kind = 'kde', secondary_y=True,ax = ax2)
ax3.plot(s_r['p'],s_r['log_return'],'k.',alpha = 0.1)
ax3.plot([x1,x2],[y1,y2],'-r')
sns.despine()
plt.tight_layout()

Ausgeschaltet[9]:

Folglich gibt es eine offensichtliche Aggregation der Volatilität und einen Hebelwirkungseffekt im Zeitreihendiagramm der logarithmischen Renditen.

Die Verzerrung im Verteilungsdiagramm der logarithmischen Renditen ist kleiner als 0, was darauf hindeutet, dass die Renditen in der Stichprobe leicht negativ und nach rechts verzerrt sind.

Die Verzerrung der Datenverteilung beträgt weniger als 1, was darauf hindeutet, dass die Ergebnisse innerhalb der Stichprobe leicht positiv und leicht rechts verzerrt sind.

Nun, da wir diesen Punkt erreicht haben, machen wir einen weiteren statistischen Test. In [7]:

line_test = pd.DataFrame(kline_all['log_return'].dropna(), dtype=np.float)
line_test.index.name = 'date'
mean = line_test.mean()
std = line_test.std()
normal_result = pd.DataFrame(index=['Mean Value', 'Std Value', 'Skewness Value','Kurtosis Value',
                                    'Ks Test Value','Ks Test P-value',
                                    'Jarque Bera Test','Jarque Bera Test P-value'],
                    columns=['model value'])
normal_result['model value']['Mean Value'] = ('%.4f'% mean[0])
normal_result['model value']['Std Value'] = ('%.4f'% std[0])
normal_result['model value']['Skewness Value'] = ('%.4f'% line_test.skew())
normal_result['model value']['Kurtosis Value'] = ('%.4f'% line_test.kurt())
normal_result['model value']['Ks Test Value'] = stats.kstest(line_test, 'norm', (mean, std))[0]
normal_result['model value']['Ks Test P-value'] = stats.kstest(line_test, 'norm', (mean, std))[1]
normal_result['model value']['Jarque Bera Test'] = stats.jarque_bera(line_test)[0]
normal_result['model value']['Jarque Bera Test P-value'] = stats.jarque_bera(line_test)[1]
normal_result

Aus[7]:

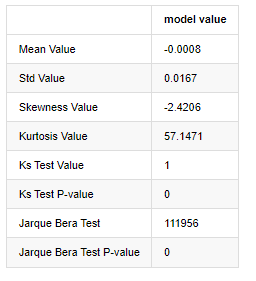
Die ursprüngliche Hypothese ist durch signifikante Differenz und normale Verteilung gekennzeichnet. Ist der P-Wert kleiner als der kritische Wert von 0,05% Konfidenzniveau, wird die ursprüngliche Hypothese abgelehnt.

Es kann gesehen werden, dass der Kurtosiswert größer als 3 ist, was die Eigenschaften von dicken Fettschwanzen zeigt. Die P-Werte von KS und JB sind kleiner als der Konfidenzintervall. Die Annahme einer normalen Verteilung wird zurückgewiesen, was beweist, dass die Rendite von BTC nicht die Eigenschaften einer normalen Verteilung hat, und die empirische Studie die Eigenschaften von dicken Fettschwanzen hat.

Vergleich der realisierten und der beobachteten Volatilität

Wir kombinieren quadratisch_log_return (logarithmische Ausbeute quadratisch) und realisiert_variance (realisierte Varianz) für Beobachtungen.

In [11]:

fig, ax = plt.subplots(figsize=(18, 6))
start = '2020-03-08 00:00:00+08:00'
end = '2020-03-20 00:00:00+08:00'

np.abs(kline_all['squared_log_return']).loc[start:end].plot(ax=ax,label='squared log return')
kline_all['realized_variance_1_hour'].loc[start:end].plot(ax=ax,label='realized variance')
plt.legend(loc='best')

Ausgeschaltet[11]:

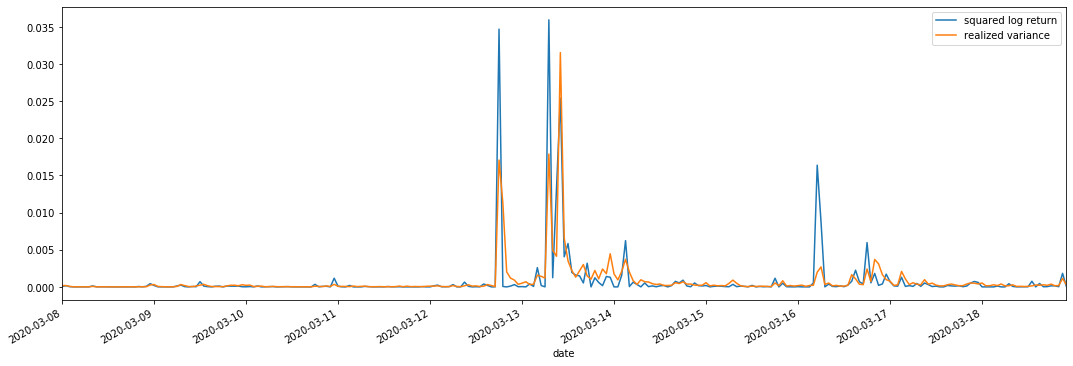
Es kann gesehen werden, dass, wenn der realisierte Varianzbereich größer ist, die Volatilität des Rendite-Bereichs auch größer ist und die realisierte Rendite glatter ist.

Aus rein theoretischer Sicht ist RV näher an der realen Volatilität, während die kurzfristige Volatilität ausgeglichen wird, da die Intraday-Volatilität zu den Übernachtdaten gehört, so dass aus beobachtender Sicht die Intraday-Volatilität für eine niedrigere Volatilitätsfrequenz am Aktienmarkt geeigneter ist.

2. Glättlichkeit der Zeitreihen

Wenn es sich um eine nicht stationäre Reihe handelt, muss sie annähernd an eine stationäre Reihe angepasst werden. Der übliche Weg ist die Differenzverarbeitung. Theoretisch kann die nicht stationäre Reihe nach vielen Malen der Differenz einer stationären Reihe annähernd entsprechen. Wenn die Kovarianz der Stichprobenreihe stabil ist, ändern sich die Erwartung, Varianz und Kovarianz ihrer Beobachtungen nicht mit der Zeit, was darauf hindeutet, dass die Stichprobenreihe für die Schlussfolgerung in der statistischen Analyse bequemer ist.

Der Einheitswurzeltest, nämlich der ADF-Test, wird hier verwendet. Der ADF-Test verwendet den t-Test, um die Signifikanz zu beobachten. Grundsätzlich werden, wenn die Reihe keinen offensichtlichen Trend zeigt, nur konstante Elemente beibehalten. Wenn die Reihe einen Trend hat, sollte die Regressionsgleichung sowohl konstante Elemente als auch Zeittrend-Elemente umfassen. Darüber hinaus können AIC- und BIC-Kriterien für die Bewertung auf der Grundlage von Informationskriterien verwendet werden. Wenn die Formel erforderlich ist, ist es wie folgt: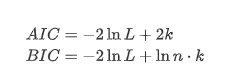

In [8]:

stable_test = kline_all['log_return']
adftest = sm.tsa.stattools.adfuller(np.array(stable_test), autolag='AIC')
adftest2 = sm.tsa.stattools.adfuller(np.array(stable_test), autolag='BIC')
output=pd.DataFrame(index=['ADF Statistic Test Value', "ADF P-value", "Lags", "Number of Observations",
                           "Critical Value(1%)","Critical Value(5%)","Critical Value(10%)"],
                    columns=['AIC','BIC'])
output['AIC']['ADF Statistic Test Value'] = adftest[0]
output['AIC']['ADF P-value'] = adftest[1]
output['AIC']['Lags'] = adftest[2]
output['AIC']['Number of Observations'] = adftest[3]
output['AIC']['Critical Value(1%)'] = adftest[4]['1%']
output['AIC']['Critical Value(5%)'] = adftest[4]['5%']
output['AIC']['Critical Value(10%)'] = adftest[4]['10%']
output['BIC']['ADF Statistic Test Value'] = adftest2[0]
output['BIC']['ADF P-value'] = adftest2[1]
output['BIC']['Lags'] = adftest2[2]
output['BIC']['Number of Observations'] = adftest2[3]
output['BIC']['Critical Value(1%)'] = adftest2[4]['1%']
output['BIC']['Critical Value(5%)'] = adftest2[4]['5%']
output['BIC']['Critical Value(10%)'] = adftest2[4]['10%']
output

Außen[8]: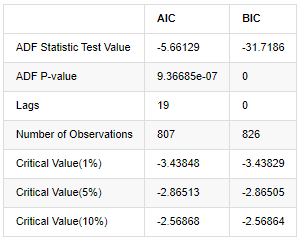

Die ursprüngliche Annahme ist, dass es keine Einheitswurzel in der Reihe gibt, d.h. die alternative Annahme ist, dass die Reihe stationär ist.

3. Modellidentifizierung und Bestellbestimmung

Um die Mittelwertgleichung zu ermitteln, ist es notwendig, einen Autocorrelationstest auf der Sequenz durchzuführen, um sicherzustellen, dass der Fehlerbegriff keine Autocorrelation hat.

In [19]:

tsplot(kline_all['log_return'], kline_all['log_return'], title='Log Return', lags=100)

Ausgeschaltet[1]:

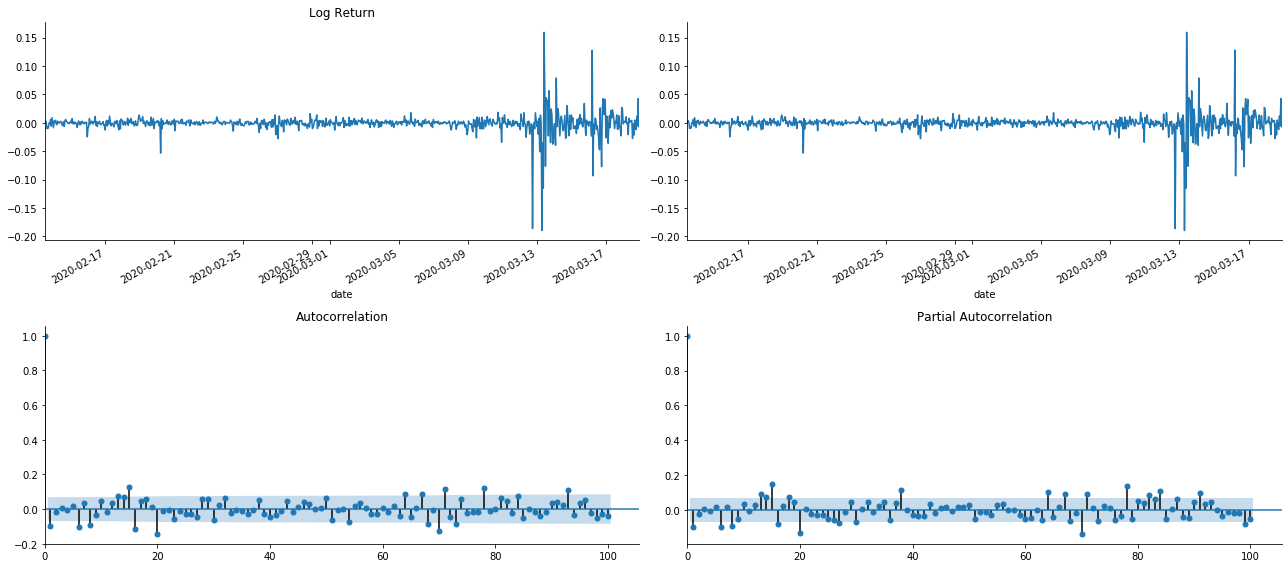
Es kann gesehen werden, dass der Effekt der Verkürzung perfekt ist. In diesem Moment gab mir dieses Bild eine Inspiration. Ist der Markt wirklich ungültig? Um zu überprüfen, werden wir Auto-Korrelationsanalyse an der Rückkehrreihe machen und die Lag-Reihenfolge des Modells bestimmen.

Der häufig verwendete Korrelationskoeffizient ist die Korrelation zwischen ihm und sich selbst zu messen, d. h. die Korrelation zwischen r(t) und r (t-l) zu einem bestimmten Zeitpunkt in der Vergangenheit: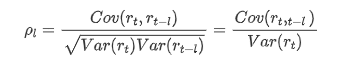

Dann machen wir einen quantitativen Test. Die ursprüngliche Annahme ist, dass alle Autocorrelationskoeffizienten 0 sind, dh es keine Autocorrelation in der Reihe gibt. Die Teststatistikformel wird wie folgt geschrieben: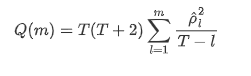

Für die Analyse wurden folgende zehn Autocorrelationskoeffizienten verwendet:

In [9]:

acf,q,p = sm.tsa.acf(kline_all['log_return'], nlags=15,unbiased=True,qstat = True, fft=False)  # Test 10 autocorrelation coefficients
output = pd.DataFrame(np.c_[range(1,16), acf[1:], q, p], columns=['lag', 'ACF', 'Q', 'P-value'])
output = output.set_index('lag')
output

Ausgeschaltet[9]: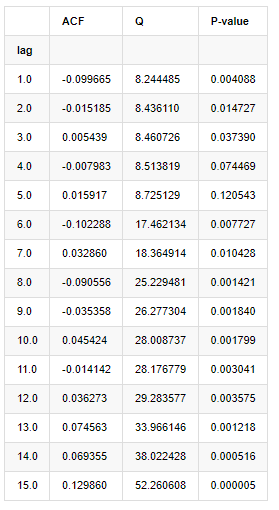

Gemäß der Teststatistik Q und P-Wert können wir sehen, dass die Autocorrelationsfunktion ACF nach der Ordnung 0 allmählich 0 wird. Die P-Werte der Q-Teststatistik sind klein genug, um die ursprüngliche Annahme zurückzuweisen, so dass es eine Autocorrelation in der Reihe gibt.

4. ARMA-Modellierung

Die AR- und MA-Modelle sind recht einfach. Einfach ausgedrückt ist Markdown zu müde, um Formeln zu schreiben. Wenn Sie interessiert sind, überprüfen Sie sie bitte selbst. Das AR-Modell (Autoregression) wird hauptsächlich zur Modellierung von Zeitreihen verwendet. Wenn die Reihe den ACF-Test bestanden hat, d.h. der Autocorrelationskoeffizient mit einem Intervall von 1 signifikant ist, d.h. die Daten zur Zeit können für die Vorhersage von Zeit t nützlich sein.

Das Modell MA (Moving Average) verwendet die zufällige Interferenz- oder Fehlervorhersage der vergangenen q-Perioden, um den aktuellen Vorhersagewert linear auszudrücken.

Um die dynamische Struktur der Daten vollständig zu beschreiben, ist es notwendig, die Reihenfolge der AR- oder MA-Modelle zu erhöhen, aber solche Parameter werden die Berechnung komplexer machen.

Da Preiszeitreihen im Allgemeinen nicht stationär sind und der Optimierungseffekt der Differenzmethode auf die Stationarität zuvor diskutiert wurde, fügt das ARIMA (p, d, q) (Summe autoregressive gleitende Durchschnitt) Modell d-Ordnungsdifferenzverarbeitung auf der Grundlage der Anwendung bestehender Modelle auf Reihen hinzu.

Kurz gesagt, der einzige Unterschied zwischen dem ARIMA-Modell und dem ARMA-Modellbauprozess besteht darin, dass das Modell, wenn die instabilen Ergebnisse nach der Analyse der Stationarität erzielt werden, eine quadratische Differenz zur Reihe unmittelbar macht und dann den Stationärtest durchführt und dann die Reihenfolge p und q bestimmt, bis die Reihe stabil ist. Nach dem Bau des Modells und der Bewertung wird die anschließende Vorhersage gemacht, wodurch der Schritt, zurückzukehren, um den Unterschied zu machen, beseitigt wird. Allerdings ist der zweite Preisunterschied bedeutungslos, so dass ARMA die beste Wahl ist.

4-1. Auswahl der Bestellung

Als nächstes können wir die Reihenfolge direkt nach dem Informationskriterium auswählen, hier versuchen wir es mit den thermodynamischen Diagrammen von AIC und BIC.

In [10]:

def select_best_params():
    ps = range(0, 4)
    ds= range(1, 2)
    qs = range(0, 4)
    parameters = product(ps, ds, qs)
    parameters_list = list(parameters)

    p_min = 0
    d_min = 0
    q_min = 0
    p_max = 3
    d_max = 3
    q_max = 3

    results_aic = pd.DataFrame(index=['AR{}'.format(i) for i in range(p_min,p_max+1)],
                               columns=['MA{}'.format(i) for i in range(q_min,q_max+1)])
    results_bic = pd.DataFrame(index=['AR{}'.format(i) for i in range(p_min,p_max+1)],
                               columns=['MA{}'.format(i) for i in range(q_min,q_max+1)])
    
    best_params = []
    aic_results = []
    bic_results = []
    hqic_results = []
    best_aic = float("inf")
    best_bic = float("inf")
    best_hqic = float("inf")
    warnings.filterwarnings('ignore')
    for param in parameters_list:
        try:
            model = sm.tsa.SARIMAX(kline_all['log_price'], order=(param[0], param[1], param[2])).fit(disp=-1)
            results_aic.loc['AR{}'.format(param[0]), 'MA{}'.format(param[2])] = model.aic
            results_bic.loc['AR{}'.format(param[0]), 'MA{}'.format(param[2])] = model.bic
        except ValueError:
            continue    
           
        aic_results.append([param, model.aic])
        bic_results.append([param, model.bic])
        hqic_results.append([param, model.hqic])
    
    results_aic = results_aic[results_aic.columns].astype(float)
    results_bic = results_bic[results_bic.columns].astype(float)
    
    # Draw thermodynamic diagrams of AIC and BIC to find the best
    fig = plt.figure(figsize=(18, 9))
    layout = (2, 2)
    aic_ax = plt.subplot2grid(layout, (0, 0))
    bic_ax = plt.subplot2grid(layout, (0, 1))

    aic_ax = sns.heatmap(results_aic,mask=results_aic.isnull(),ax=aic_ax,cmap='OrRd',annot=True,fmt='.2f',);
    aic_ax.set_title('AIC');
    bic_ax = sns.heatmap(results_bic,mask=results_bic.isnull(),ax=bic_ax,cmap='OrRd',annot=True,fmt='.2f',);
    bic_ax.set_title('BIC');
    
    aic_df = pd.DataFrame(aic_results)
    aic_df.columns = ['params', 'aic']   
    best_params.append(aic_df.params[aic_df.aic.idxmin()])
    print('AIC best param: {}'.format(aic_df.params[aic_df.aic.idxmin()]))
    
    bic_df = pd.DataFrame(bic_results)
    bic_df.columns = ['params', 'bic']
    best_params.append(bic_df.params[bic_df.bic.idxmin()])
    print('BIC best param: {}'.format(bic_df.params[bic_df.bic.idxmin()]))
    
    hqic_df = pd.DataFrame(hqic_results)
    hqic_df.columns = ['params', 'hqic']
    best_params.append(hqic_df.params[hqic_df.hqic.idxmin()])
    print('HQIC best param: {}'.format(hqic_df.params[hqic_df.hqic.idxmin()]))

    for best_param in best_params:
        if best_params.count(best_param)>=2:
            print('Best Param Selected: {}'.format(best_param))
            return best_param 

best_param = select_best_params()

Ausgeschaltet[10]: Bestparam AIC: (0, 1, 1) BIC beste Param: (0, 1, 1) HQIC beste Param: (0, 1, 1) Beste Param ausgewählt: (0, 1, 1)

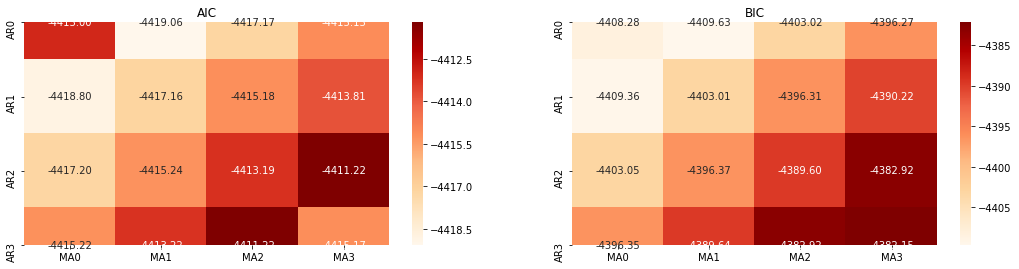
Es ist offensichtlich, dass die optimale Parameterkombination erster Ordnung für den logarithmischen Preis (0,1,1) ist, was einfach und unkompliziert ist. Die log_return (logarithmische Rendite) führt die gleiche Operation aus. Der optimale AIC-Wert ist (4,3), und der optimale BIC-Wert ist (0,1). Die optimale Kombination von Parametern für log_return (logarithmische Rendite) ist also (0,1).

4-2 Modellierung und Abgleich von ARMA

Vierteljährliche Koeffizienten sind nicht erforderlich, aber SARIMAX ist reicher an Eigenschaften, daher wurde beschlossen, dieses Modell für die Modellierung zu wählen und nebenbei eine beschreibende Analyse wie folgt zu erstellen:

In [11]:

params = (0, 0, 1)
training_model = smt.SARIMAX(endog=kline_all['log_return'], trend='c', order=params, seasonal_order=(0, 0, 0, 0))
model_results = training_model.fit(disp=False)
model_results.summary()

Ausgeschaltet[11]: Ergebnisse des Statespace-Modells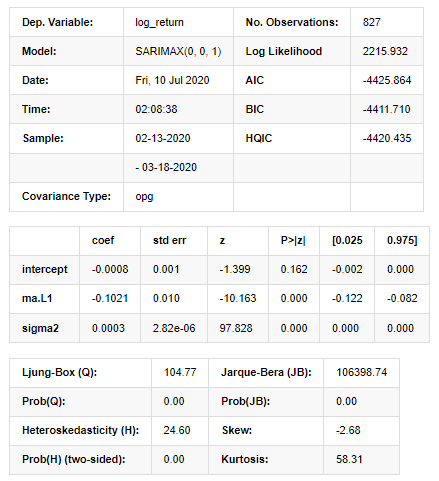

Warnungen: [1] Mitvarianzmatrix berechnet anhand des äußeren Produkts der Gradienten (komplexe Stufe). In [27]:

model_results.plot_diagnostics(figsize=(18, 10));

Ausgeschaltet[1]:

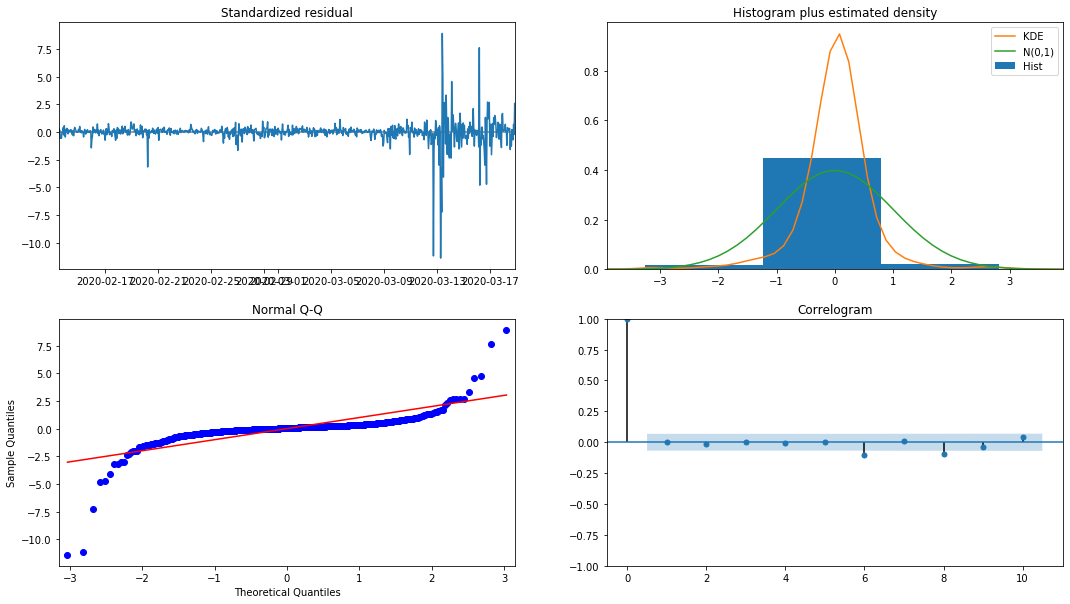
Die Wahrscheinlichkeitsdichte KDE im Histogramm ist weit von der Normalverteilung N (0,1) entfernt, was darauf hindeutet, dass der Restwert keine Normalverteilung ist.

Dann muss jedoch noch geprüft werden, ob das Modell verwendet werden kann.

4-3. Modellprüfung

Der Matching-Effekt des Restwerts ist nicht ideal, daher führten wir den Durbin-Watson-Test durch. Die ursprüngliche Hypothese des Tests ist, dass die Sequenz keine Autocorrelation hat und die alternative Hypothese-Sequenz stationär ist. Außerdem wird die ursprüngliche Hypothese abgelehnt, wenn die P-Werte der LB-, JB- und H-Tests kleiner als der kritische Wert von 0,05% Konfidenzniveau sind.

In [12]:

het_method='breakvar'
norm_method='jarquebera'
sercor_method='ljungbox'

(het_stat, het_p) = model_results.test_heteroskedasticity(het_method)[0]
norm_stat, norm_p, skew, kurtosis = model_results.test_normality(norm_method)[0]

sercor_stat, sercor_p = model_results.test_serial_correlation(method=sercor_method)[0]
sercor_stat = sercor_stat[-1] # The last value of the maximum period
sercor_p = sercor_p[-1]

dw = sm.stats.stattools.durbin_watson(model_results.filter_results.standardized_forecasts_error[0, model_results.loglikelihood_burn:])

arroots_outside_unit_circle = np.all(np.abs(model_results.arroots) > 1)
maroots_outside_unit_circle = np.all(np.abs(model_results.maroots) > 1)

print('Test heteroskedasticity of residuals ({}): stat={:.3f}, p={:.3f}'.format(het_method, het_stat, het_p));
print('\nTest normality of residuals ({}): stat={:.3f}, p={:.3f}'.format(norm_method, norm_stat, norm_p));
print('\nTest serial correlation of residuals ({}): stat={:.3f}, p={:.3f}'.format(sercor_method, sercor_stat, sercor_p));
print('\nDurbin-Watson test on residuals: d={:.2f}\n\t(NB: 2 means no serial correlation, 0=pos, 4=neg)'.format(dw))
print('\nTest for all AR roots outside unit circle (>1): {}'.format(arroots_outside_unit_circle))
print('\nTest for all MA roots outside unit circle (>1): {}'.format(maroots_outside_unit_circle))

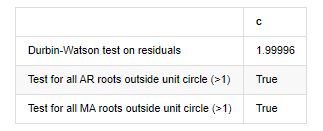
root_test=pd.DataFrame(index=['Durbin-Watson test on residuals','Test for all AR roots outside unit circle (>1)','Test for all MA roots outside unit circle (>1)'],columns=['c'])
root_test['c']['Durbin-Watson test on residuals']=dw
root_test['c']['Test for all AR roots outside unit circle (>1)']=arroots_outside_unit_circle
root_test['c']['Test for all MA roots outside unit circle (>1)']=maroots_outside_unit_circle
root_test

Ausgeschaltet: Versuchsheteroskedasticität der Rückstände (Breakvar): stat=24,598, p=0.000

Testnormalität der Rückstände (Jarquebera): stat=106398.739, p=0.000

Testreihe Korrelation der Rückstände (Ljungbox): stat=104.767, p=0.000

Durbin-Watson-Test für Rückstände: d=2,00 (Hinweis: 2 bedeutet keine serielle Korrelation, 0=pos, 4=negativ)

Prüfung für alle AR-Wurzeln außerhalb des Einheitskreises (>1): Richtig

Prüfung für alle MA-Wurzeln außerhalb des Einheitskreises (>1): Richtig

In [13]:

kline_all['log_price_dif1'] = kline_all['log_price'].diff(1)
kline_all = kline_all[1:]
kline_train = kline_all

training_label = 'log_return'
training_ts = pd.DataFrame(kline_train[training_label], dtype=np.float)

delta = model_results.fittedvalues - training_ts[training_label]
adjR = 1 - delta.var()/training_ts[training_label].var()
adjR_test=pd.DataFrame(index=['adjR2'],columns=['Value'])
adjR_test['Value']['adjR2']=adjR**2
adjR_test

Aus dem Spiel[13]:

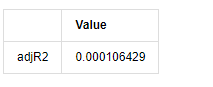
Wenn die Durbin-Watson-Teststatistik gleich 2 ist, bestätigt dies, dass die Reihe keine Korrelation hat und ihr statistischer Wert zwischen (0,4) verteilt ist. Nahe bei 0 bedeutet, dass die positive Korrelation hoch ist, während nahe bei 4 bedeutet, dass die negative Korrelation hoch ist. Hier ist es ungefähr gleich 2. Der P-Wert anderer Tests ist klein genug, die Einheitsmerkmalwurzel befindet sich außerhalb des Einheitskreises, und je größer der Wert des modifizierten adjR2 ist, desto besser wird er sein. Das Gesamtergebnis der Messung scheint nicht zufriedenstellend zu sein.

In [14]:

model_results.params

Ausgeschaltet[1]: Abfangen -0.000817 Ma.L1 -0.102102 Sigma2 0,000275 dTyp: Schwimmer 64

Zusammenfassend lässt sich sagen, dass dieser Bestellparameter grundsätzlich die Anforderungen der Modellierung von Zeitreihen und der anschließenden Volatilitätsmodellierung erfüllen kann, aber der Matching-Effekt ist so-so.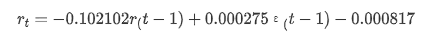

Modellvorhersage

Als nächstes wird das trainierte Modell nach vorne abgestimmt. statsmodels bietet statische und dynamische Optionen für das Abgleichen und Vorhersagen. Der Unterschied liegt darin, ob der Beobachtungswert im nächsten Schritt der Vorhersage verwendet wird oder der im vorherigen Schritt generierte Vorhersagewert iterativ verwendet wird. Die Vorhersageeffekte von log_return (logarithmische Rendite) sind wie folgt:

In [37]:

start_date = '2020-02-28 12:00:00+08:00'
end_date = start_date 

pred_dy = model_results.get_prediction(start=start_date, dynamic=False)
pred_dy_ci = pred_dy.conf_int()

fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(18, 6))
ax.plot(kline_all['log_return'].loc[start_date:], label='Log Return', linestyle='-')
ax.plot(pred_dy.predicted_mean.loc[start_date:], label='Forecast Log Return', linestyle='--')
ax.fill_between(pred_dy_ci.index,pred_dy_ci.iloc[:, 0],pred_dy_ci.iloc[:, 1], color='g', alpha=.25)

plt.ylabel("BTC Log Return")
plt.legend(loc='best')
plt.tight_layout()
sns.despine()

Außen [1]:

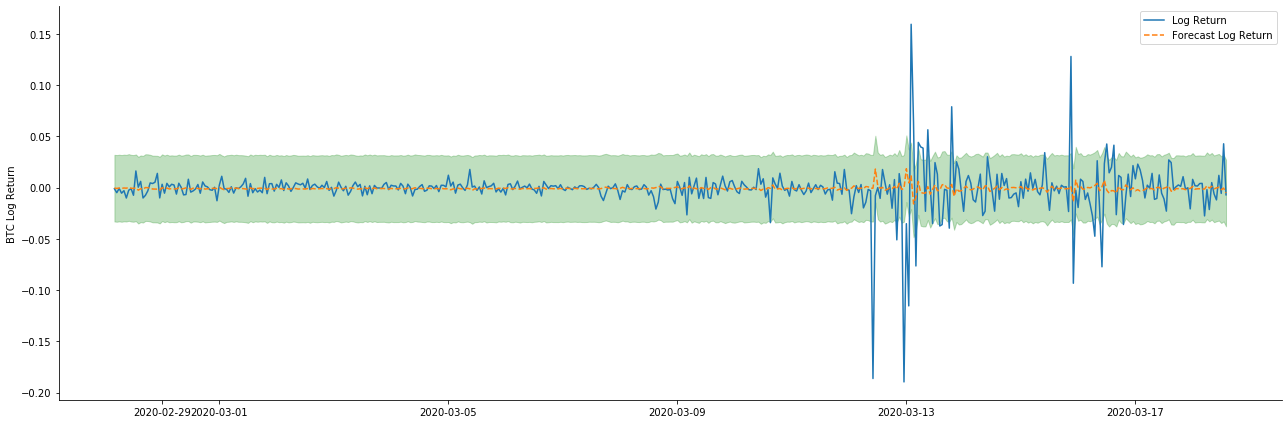
Es kann festgestellt werden, daß die Anpassung des statischen Modus auf die Probe hervorragend ist, die Probendaten mit einem Konfidenzintervall von nahezu 95% abgedeckt werden können und der dynamische Modus etwas außer Kontrolle gerät.

Schauen wir uns also den Effekt der Datenvergleichung im dynamischen Modus an:

In [38]:

start_date = '2020-02-28 12:00:00+08:00'
end_date = start_date 

pred_dy = model_results.get_prediction(start=start_date, dynamic=True)
pred_dy_ci = pred_dy.conf_int()

fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(18, 6))
ax.plot(kline_all['log_return'].loc[start_date:], label='Log Return', linestyle='-')
ax.plot(pred_dy.predicted_mean.loc[start_date:], label='Forecast Log Return', linestyle='--')
ax.fill_between(pred_dy_ci.index,pred_dy_ci.iloc[:, 0],pred_dy_ci.iloc[:, 1], color='g', alpha=.25)

plt.ylabel("BTC Log Return")
plt.legend(loc='best')
plt.tight_layout()
sns.despine()

Außen [1]:

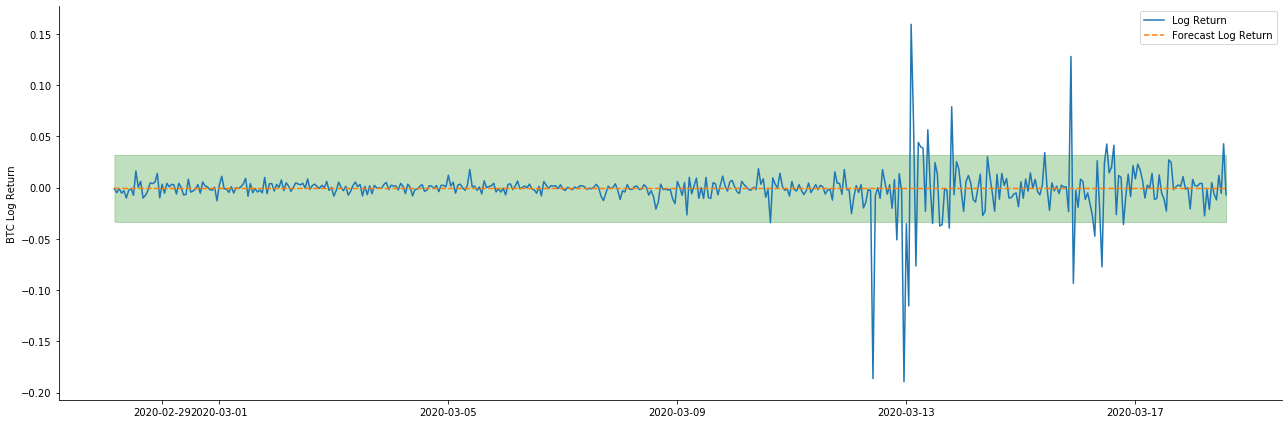
Es wird festgestellt, daß der Passwirkung der beiden Modelle auf die Stichprobe eine ausgezeichnete Bedeutung zukommt und daß der Mittelwert fast durch das 95%-Konfidenzintervall abgedeckt werden kann, aber das statische Modell ist offensichtlich besser geeignet.

In [41]:

# Out-of-sample predicted data predict()
start_date = '2020-03-01 12:00:00+08:00'
end_date = '2020-03-20 23:00:00+08:00'
model = False

predict_step = 50
predicts_ARIMA_normal = model_results.get_prediction(start=start_date, dynamic=model, full_reports=True)
ci_normal = predicts_ARIMA_normal.conf_int().loc[start_date:]

predicts_ARIMA_normal_out = model_results.get_forecast(steps=predict_step, dynamic=model)
ci_normal_out = predicts_ARIMA_normal_out.conf_int().loc[start_date:end_date]

fig, ax = plt.subplots(figsize=(18,8))
kline_test.loc[start_date:end_date, 'log_return'].plot(ax=ax, label='Benchmark Log Return')

predicts_ARIMA_normal.predicted_mean.plot(ax=ax, style='g', label='In Sample Forecast')
ax.fill_between(ci_normal.index, ci_normal.iloc[:,0], ci_normal.iloc[:,1], color='g', alpha=0.1)

predicts_ARIMA_normal_out.predicted_mean.loc[:end_date].plot(ax=ax, style='r--', label='Out of Sample Forecast')
ax.fill_between(ci_normal_out.index, ci_normal_out.iloc[:,0], ci_normal_out.iloc[:,1], color='r', alpha=0.1)

plt.tight_layout()
plt.legend(loc='best')
sns.despine()

Aus dem Spiel:

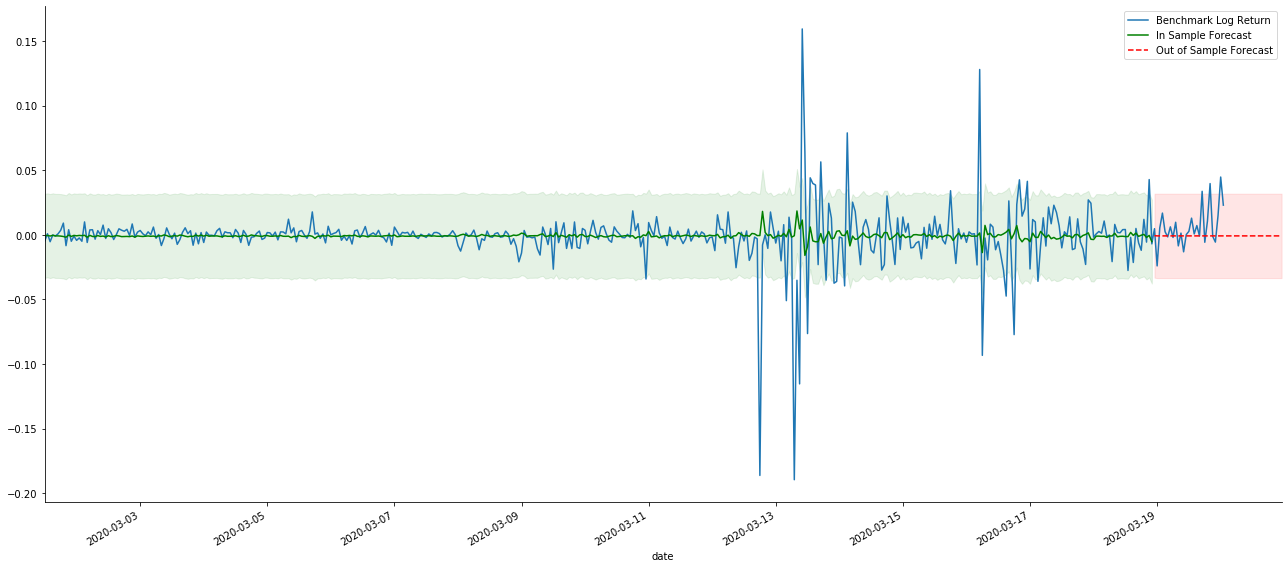
Da die Übereinstimmung von Daten in der Stichprobe eine rollende Vorhersage ist, ist das statische Modell anfällig für Übermatching, während das dynamische Modell keine zuverlässigen abhängigen Variablen hat und der Effekt nach der Iteration immer schlimmer wird.

Wenn wir die erwartete Rendite auf log_price (logarithmischer Preis) umkehren, wird die Übereinstimmung in der folgenden Abbildung dargestellt:

In [42]:

params = (0, 1, 1)
mod = smt.SARIMAX(endog=kline_all['log_price'], trend='c', order=params, seasonal_order=(0, 0, 0, 0))
res = mod.fit(disp=False)

start_date = '2020-03-01 12:00:00+08:00'
end_date = '2020-03-15 23:00:00+08:00'

predicts_ARIMA_normal = res.get_prediction(start=start_date, dynamic=False, full_results=False)
predicts_ARIMA_dynamic = res.get_prediction(start=start_date, dynamic=True, full_results=False)

fig, ax = plt.subplots(figsize=(18,6))
kline_test.loc[start_date:end_date, 'log_price'].plot(ax=ax, label='Log Price')

predicts_ARIMA_normal.predicted_mean.loc[start_date:end_date].plot(ax=ax, style='r--', label='Normal Prediction')
ci_normal = predicts_ARIMA_normal.conf_int().loc[start_date:end_date]
ax.fill_between(ci_normal.index, ci_normal.iloc[:,0], ci_normal.iloc[:,1], color='r', alpha=0.1)

predicts_ARIMA_dynamic.predicted_mean.loc[start_date:end_date].plot(ax=ax, style='g', label='Dynamic Prediction')
ci_dynamic = predicts_ARIMA_dynamic.conf_int().loc[start_date:end_date]
ax.fill_between(ci_dynamic.index, ci_dynamic.iloc[:,0], ci_dynamic.iloc[:,1], color='g', alpha=0.1)

plt.tight_layout()
plt.legend(loc='best')
sns.despine()

Aus dem Spiel:

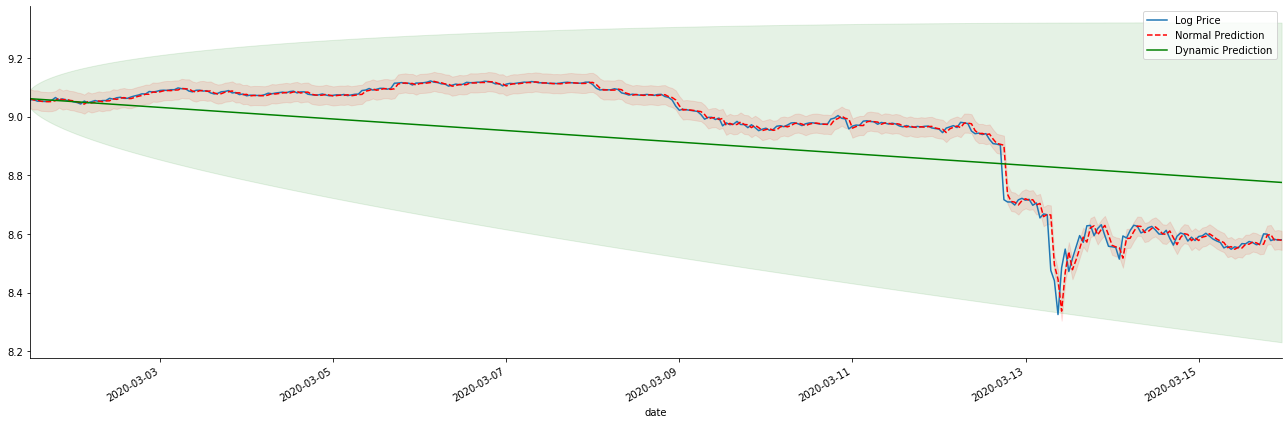
Es ist leicht zu sehen, die passenden Vorteile des statischen Modells und den extremen Unterschied zwischen dem dynamischen Modell und dem statischen Modell in der langfristigen Vorhersage. Die rote gestrichelte Linie und der rosa Bereich... Sie können nicht sagen, dass die Vorhersage dieses Modells falsch ist. Schließlich deckt es den Trend des gleitenden Durchschnitts vollständig ab, aber... ist es sinnvoll?

In der Tat ist das ARMA-Modell selbst nicht falsch, denn das Problem ist nicht das Modell selbst, sondern die objektive Logik der Dinge selbst. Das Zeitreihenmodell kann nur auf der Grundlage der Korrelation zwischen vorherigen und nachfolgenden Beobachtungen hergestellt werden. Daher ist es unmöglich, die White-Noise-Serie zu modellieren. Daher basiert alle vorherige Arbeit auf einer kühnen Annahme, dass die Rendite-Rate-Serie von BTC nicht unabhängig und identisch verteilt sein kann.

Im Allgemeinen sind die Renditenreihen Martingale-Differenzreihen, was bedeutet, dass die Rendite unvorhersehbar ist und die schwache Effizienzannahme des entsprechenden Marktes gilt. Wir haben angenommen, dass die Renditen in einzelnen Proben einen gewissen Grad an Auto-Korrelation haben, und die gleiche Verteilungsannahme ist auch, das Matching-Modell für das Trainings-Set anwendbar zu machen, so dass ein einfaches ARMA-Modell abgestimmt werden kann, das eine schlechte Vorhersagewirkung haben wird.

Die Martingale-Differenzsequenz ist möglicherweise nicht unabhängig und identisch verteilt, aber die bedingte Varianz kann vom vergangenen Wert abhängen, so dass die Autocorrelation erster Ordnung verschwunden ist, aber es gibt immer noch eine Autocorrelation höherer Ordnung, die auch eine wichtige Voraussetzung für die Modellierung und Beobachtung der Volatilität ist.

Wenn eine solche Logik zutrifft, dann gilt auch die Prämisse des Aufbaus verschiedener Volatilitätsmodelle. Also für eine Rendite-Rate-Serie, wenn ein schwach effizienter Markt zufrieden ist, dann muss der mittlere Wert schwer vorherzusagen sein, aber die Varianz ist vorhersehbar. Und die abgestimmte ARMA bietet einen fairen Qualitäts-Zeitreihe-Benchmark, dann bestimmt die Qualität auch die Qualität der Volatilitätsvorhersage.

Schließlich lassen Sie uns die Wirkung der Vorhersage einfach bewerten: Bei Fehler als Bewertungsanalyse sind die Indikatoren innerhalb und außerhalb der Stichprobe wie folgt:

In [15]:

start = '2020-02-14 00:00:00+08:00'
predicts_ARIMA_normal = model_results.get_prediction(dynamic=False)
predicts_ARIMA_dynamic = model_results.get_prediction(dynamic=True)
training_label = 'log_return'

compare_ARCH_X = pd.DataFrame()
compare_ARCH_X['Model'] = ['NORMAL','DYNAMIC']
compare_ARCH_X['RMSE'] = [rmse(predicts_ARIMA_normal.predicted_mean[1:], kline_test[training_label][:826]),
                          rmse(predicts_ARIMA_dynamic.predicted_mean[1:], kline_test[training_label][:826])]
compare_ARCH_X['MAPE'] = [mape(predicts_ARIMA_normal.predicted_mean[:50], kline_test[training_label][:50]),
                          mape(predicts_ARIMA_dynamic.predicted_mean[:50], kline_test[training_label][:50])]
compare_ARCH_X

Ausgeschaltet[1]: Wurzeldurchschnittlicher Quadratfehler (RMSE): 0,0184 Wurzeldurchschnittlicher Quadratfehler (RMSE): 0,0167 Durchschnittlicher absoluter Fehleranteil (MAPE): 2,25e+03 Durchschnittlicher absoluter Fehleranteil (MAPE): 395

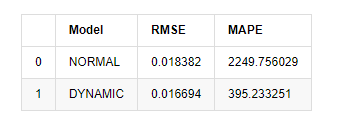
Es kann gesehen werden, dass das statische Modell in Bezug auf den Fehlerzusammenfall zwischen dem vorhergesagten Wert und dem realen Wert etwas besser ist als das dynamische Modell. Es entspricht der logarithmischen Rendite von Bitcoin gut, was im Wesentlichen den Erwartungen entspricht. Der dynamischen Vorhersage fehlt eine genauere Variableninformation, und der Fehler wird auch durch Iteration vergrößert, so dass der Vorhersageffekt schlecht ist. MAPE ist größer als 100%, so dass die tatsächliche Übereinstimmungsqualität beider Modelle nicht ideal ist.

In [18]:

predict_step = 50
predicts_ARIMA_normal_out = model_results.get_forecast(steps=predict_step, dynamic=False)
predicts_ARIMA_dynamic_out = model_results.get_forecast(steps=predict_step, dynamic=True)
testing_ts = kline_test
training_label = 'log_return'

compare_ARCH_X = pd.DataFrame()
compare_ARCH_X['Model'] = ['NORMAL','DYNAMIC']
compare_ARCH_X['RMSE'] = [get_rmse(predicts_ARIMA_normal_out.predicted_mean, testing_ts[training_label]),
                          get_rmse(predicts_ARIMA_dynamic_out.predicted_mean, testing_ts[training_label])]
compare_ARCH_X['MAPE'] = [get_mape(predicts_ARIMA_normal_out.predicted_mean, testing_ts[training_label]),
                          get_mape(predicts_ARIMA_dynamic_out.predicted_mean, testing_ts[training_label])]
compare_ARCH_X

Ausgeschaltet[1]:

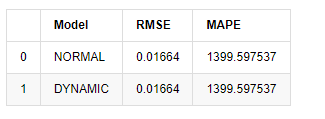
Da die nächste Vorhersage außerhalb der Stichprobe von den Ergebnissen des vorherigen Schrittes abhängt, ist nur das dynamische Modell wirksam. Der langfristige Fehlerfehler des dynamischen Modells führt jedoch zu einer unzureichenden Vorhersagekraft des Gesamtmodells, so dass der nächste Schritt höchstens vorhergesagt wird.

Zusammenfassend ist das statische Modell des ARMA-Modells geeignet, um die Intra-Sample-Rendite von Bitcoin abzugleichen. Die kurzfristige Vorhersage der Rendite kann den Konfidenzintervall effektiv abdecken, aber die langfristige Vorhersage ist sehr schwierig, was der schwachen Effektivität des Marktes entspricht.

5. ARCH-Effekt

Der ARCH-Modell-Effekt ist die Reihe Korrelation der bedingten Heteroscedasticity-Sequenz. Der Mischungs-Test Ljung Box wird verwendet, um die Korrelation der Restquadratreihe zu testen, um festzustellen, ob es einen ARCH-Effekt gibt. Wenn der ARCH-Effekt-Test bestanden wird, d.h. die Reihe hat Heteroscedasticity, kann der nächste Schritt der GARCH-Modellierung durchgeführt werden, um die mittlere Gleichung und die Volatilitätsgleichung gemeinsam zu schätzen. Andernfalls muss das Modell optimiert und neu eingestellt werden, wie zum Beispiel Differentialverarbeitung oder wechselseitige Reihen.

Wir bereiten hier einige Datensätze und globale Variablen vor:

In [33]:

count_num = 100000
start_date = '2020-03-01'

df = get_bars('huobi.btc_usdt', '1m', count=count_num, start=start_date)  # Take the minute data
kline_1m = pd.DataFrame(df['close'], dtype=np.float)
kline_1m.index.name = 'date'
kline_1m['log_price'] = np.log(kline_1m['close'])
kline_1m['return'] = kline_1m['close'].pct_change().dropna()
kline_1m['log_return'] = kline_1m['log_price'] - kline_1m['log_price'].shift(1)

kline_1m['squared_log_return'] = np.power(kline_1m['log_return'], 2)

kline_1m['return_100x'] = np.multiply(kline_1m['return'], 100)
kline_1m['log_return_100x'] = np.multiply(kline_1m['log_return'], 100)  # Enlarge 100 times

df = get_bars('huobi.btc_usdt', '1h', count=count_num, start=start_date)  # Take the hour data
kline_test = pd.DataFrame(df['close'], dtype=np.float)
kline_test.index.name = 'date'
kline_test['log_price'] = np.log(kline_test['close'])  # Calculate the daily logarithmic rate of return
kline_test['return'] = kline_test['log_price'].pct_change().dropna()
kline_test['log_return'] = kline_test['log_price'] - kline_test['log_price'].shift(1)  # Calculate the logarithmic rate of return
kline_test['squared_log_return'] = np.power(kline_test['log_return'], 2)  # Exponential square of log daily return rate

kline_test['return_100x'] = np.multiply(kline_test['return'], 100)
kline_test['log_return_100x'] = np.multiply(kline_test['log_return'], 100)  # Enlarge 100 times

kline_test['realized_variance_1_hour'] = kline_1m.loc[:, 'squared_log_return'].resample('h', closed='left', label='left').sum().copy() # Resampling to days 
kline_test['realized_volatility_1_hour'] = np.sqrt(kline_test['realized_variance_1_hour'])  # Volatility of variance derivation

kline_test = kline_test[4:-2500]
kline_test.head(3)

Außen [1]:

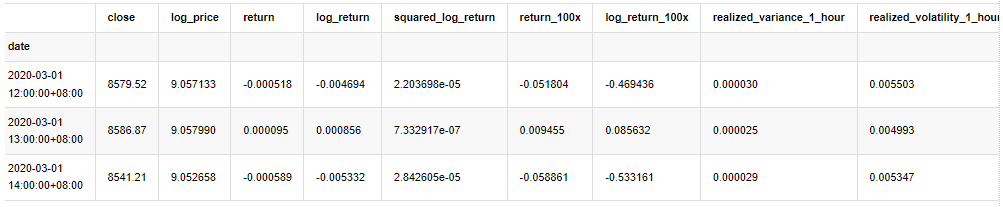
In [22]:

cc = 3
model_p = 1
predict_lag = 30
label = 'log_return'

training_label = label
training_ts = pd.DataFrame(kline_test[training_label], dtype=np.float)

training_arch_label = label
training_arch = pd.DataFrame(kline_test[training_arch_label], dtype=np.float)

training_garch_label = label
training_garch = pd.DataFrame(kline_test[training_garch_label], dtype=np.float)

training_egarch_label = label
training_egarch = pd.DataFrame(kline_test[training_egarch_label], dtype=np.float)

training_arch.plot(figsize = (18,4))

Außen [1]: Das ist ein sehr schwieriger Fall.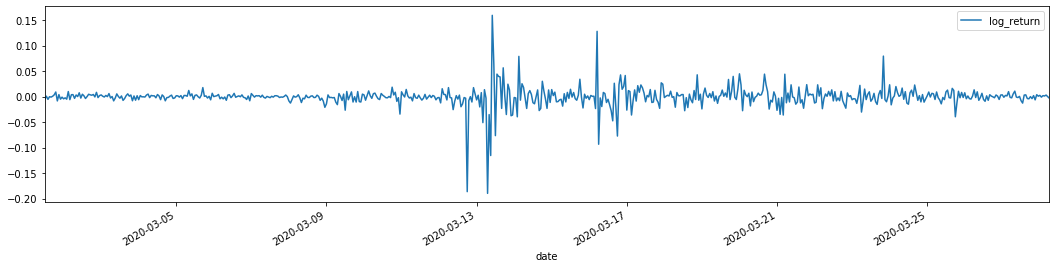

Die logarithmischen Rücklaufraten sind oben dargestellt. Als nächstes müssen wir den ARCH-Effekt der Probe testen. Wir ermitteln die Restreihe innerhalb der Probe auf Basis von ARMA.

In [20]:

training_arma_model = smt.SARIMAX(endog=training_ts, trend='c', order=(0, 0, 1), seasonal_order=(0, 0, 0, 0))
arma_model_results = training_arma_model.fit(disp=False)
arma_model_results.summary()
training_arma_fitvalue = pd.DataFrame(arma_model_results.fittedvalues,dtype=np.float)
at = pd.merge(training_ts, training_arma_fitvalue, on='date')
at.columns = ['log_return', 'model_fit']
at['res'] = at['log_return'] - at['model_fit']
at['res2'] = np.square(at['res'])
at.head()

Ausgeschaltet[1]:

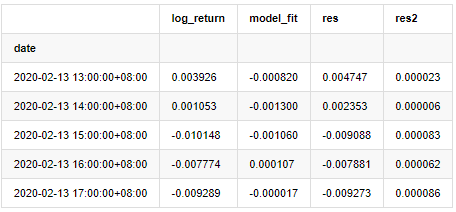
Anschließend wird die Restreihe der Stichprobe dargestellt.

In [69]:

fig, ax = plt.subplots(figsize=(18, 6))
ax1 = fig.add_subplot(2,1,1)
at['res'][1:].plot(ax=ax1,label='resid')
plt.legend(loc='best')

ax2 = fig.add_subplot(2,1,2)
at['res2'][1:].plot(ax=ax2,label='resid2')

plt.legend(loc='best')
plt.tight_layout()
sns.despine()

Außen [1]:

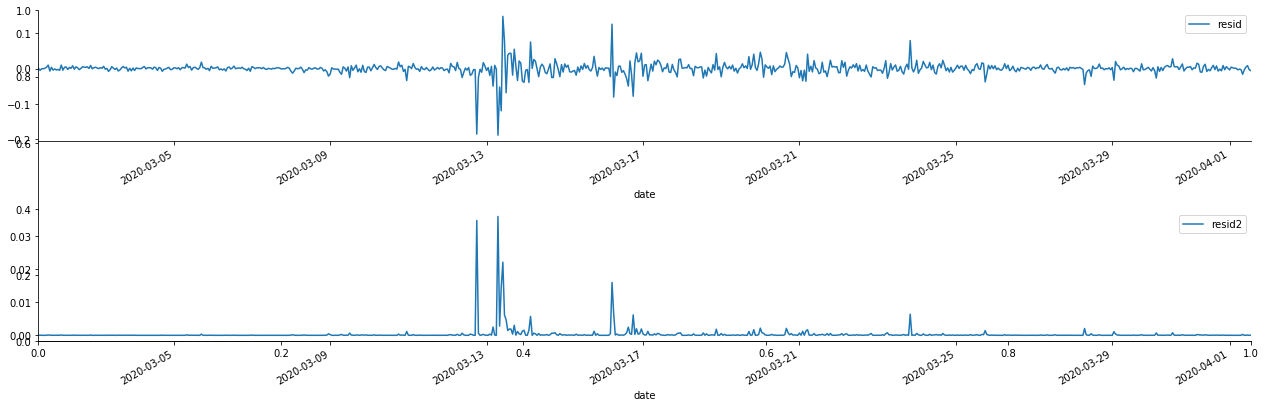
Es kann gesehen werden, dass die Restreihe offensichtliche Aggregationseigenschaften aufweist, und man kann zunächst beurteilen, dass die Reihe einen ARCH-Effekt hat.

In [70]:

figure = plt.figure(figsize=(18,4))
ax1 = figure.add_subplot(111)
fig = sm.graphics.tsa.plot_acf(at['res2'],lags = 40, ax=ax1)

Ausgeschaltet[70]:

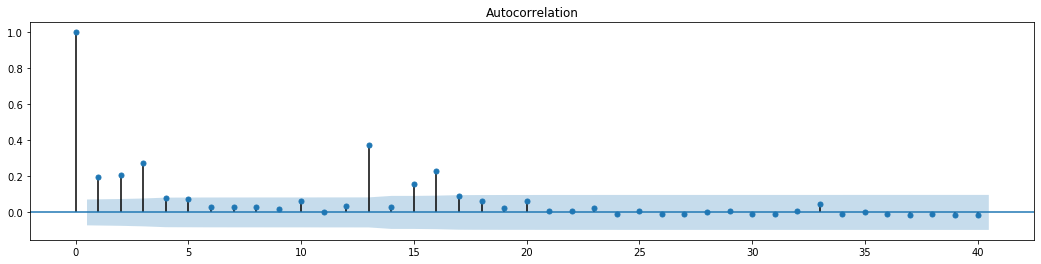
Die ursprüngliche Annahme für den Serie-Blending-Test ist, dass die Reihe keine Korrelation hat. Es kann gesehen werden, dass die entsprechenden P-Werte der ersten 20 Datenordnungen kleiner sind als der kritische Wert des Konfidenzniveaus von 0,05%. Daher wird die ursprüngliche Annahme abgelehnt, dh der Rest der Reihe hat den ARCH-Effekt. Das Varianzmodell kann über das ARCH-Typmodell erstellt werden, um die Heteroscedastik der Restreihe anzupassen und die Volatilität weiter vorherzusagen.

6. GARCH-Modellierung

Bevor wir die GARCH-Modellierung durchführen, müssen wir uns mit dem Fettschwanzteil der Reihe befassen. Weil der Fehlerbegriff der Reihe in der Hypothese der Normalverteilung oder der t-Verteilung entspricht, und wir haben zuvor überprüft, dass die Ertragsreihe eine Fettschwanzverteilung hat, müssen wir diesen Teil beschreiben und ergänzen.

In der GARCH-Modellierung liefert der Fehlerpunkt die Optionen der Normalverteilung, der t-Verteilung, der GED (Generalized Error Distribution) und der Skewed Students t-Verteilung.

Verwandt

Mehr