Compréhension intuitive de la cointégration

Le but de cet article est de vous présenter le concept de l’intégration de manière intuitive, de vous aider à comprendre sa signification fondamentale, les motivations qu’il soulève et les scénarios d’application simples.

• Résumé de l’intégration

J’aimerais simplement souligner que la définition intuitive de l’intégrité n’implique pas la définition d’un symbole mathématique strict et la déduction d’une formule stricte.

Si vous êtes intéressé, vous pouvez vous référer à: Wikipedia Cointegration.

Pourquoi l’uniformité ?

Il y a une certaine stabilité à l’intégration.

En termes simples, la stationarité est la propriété d’une séquence qui reste stable dans le temps. C’est une propriété que nous apprécions beaucoup lorsque nous faisons des prévisions analytiques sur des données. Si un ensemble de données de séquence temporelle est stable, cela signifie que ses moyennes et différences restent inchangées, ce qui nous permet d’utiliser facilement certaines techniques statistiques sur la séquence.

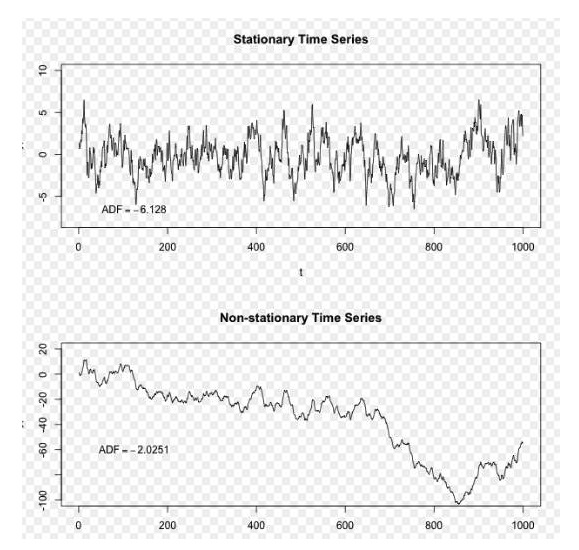
Une image de la photo de l’auteur de ce billet.

Dans la figure ci-dessus, la séquence en haut est une séquence stable, et nous pouvons voir qu’elle est toujours en mouvement autour d’une moyenne à long terme, la séquence en bas est une séquence non stable, et nous pouvons voir que sa moyenne à long terme est variable.

Par exemple, si la séquence de prix d’un actif (ou la différence entre deux séquences) est stable, on peut s’attendre à ce que le prix revienne à cette valeur à un moment donné dans l’avenir, après s’être écarté de sa valeur moyenne. On peut utiliser cette propriété pour investir et ainsi tirer un profit. Supposons qu’une action a une valeur moyenne à long terme de 9 dollars et une valeur actuelle de 8 dollars.

Voici une séquence de prix d’actions de nature régulière:

Si les deux ensembles de séquences ne sont pas stables, mais que leur combinaison linéaire donne une séquence stable, alors nous disons que les deux ensembles de données de séquences temporelles ont la même propriété de cohésion, et nous pouvons également appliquer la même propriété statistique à la séquence de cette combinaison. Mais il faut souligner que la cohésion n’est pas une relation de corrélation.

Par exemple, si l’écart entre deux séries de données de séries chronologiques est stable, nous pouvons investir et nous rentabiliser en fonction de cette stabilité: lorsque le prix des deux actions est trop différent, nous nous attendons à ce que l’écart de prix se rapproche en fonction de la stabilité. Nous achetons donc des actions à bas prix, vendons des actions à bas prix et attendons que le prix revienne.

C’est de là que vient le commerce des paires.

• Stabilité et méthodes de test

Strictement parlant, la stabilité peut être divisée en deux catégories: la stabilité stricte (strictly stationary) et la stabilité faible (c’est-à-dire la stabilité de coïncidence, la stabilité de covariance, etc.). La stabilité stricte désigne une séquence qui a toujours une fonction de distribution inchangée, tandis que la stabilité faible désigne une statistique descriptive de la constante de la séquence.

Un exemple d’application

Tout d’abord, il est important de souligner que la corrélation n’est pas une corrélation. Nous avons artificiellement construit deux ensembles de données, ce qui nous a permis de visualiser la corrélation. import numpy as np import pandas as pd import seaborn import statsmodels import matplotlib.pyplot as plt from statsmodels.tsa.stattools import coint

Données structurées

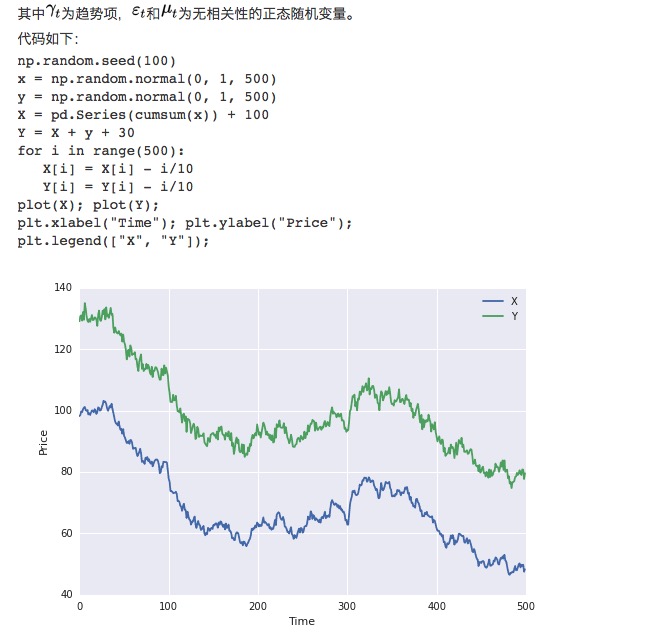
Tout d’abord, nous construisons deux ensembles de données de 100 de longueur chacun. Le premier groupe de données est 100 plus un élément de tendance à la baisse et une distribution normale. Le second groupe de données est construit sur la base du premier groupe de données, plus 30 et une distribution normale supplémentaire.

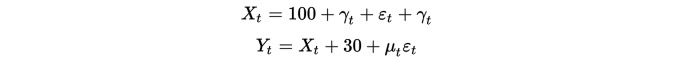
De toute évidence, les deux ensembles de données sont non-stables, car la moyenne change avec le temps. Mais les deux ensembles de données sont cohérents, car leur séquence de différence est stable:

plot(Y-X); plt.axhline((Y-X).mean(),color=“red”, linestyle=“–”); plt.xlabel(“Time”); plt.ylabel(“Price”); plt.legend([“Y-X”, “Mean”]);

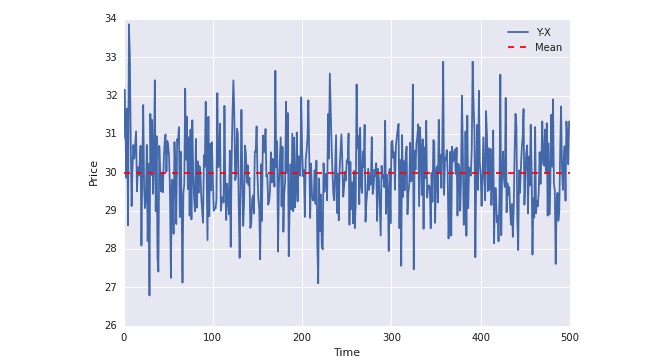
Dans le graphique ci-dessus, on peut voir que la ligne bleue fluctue constamment autour de la moyenne. La moyenne ne change pas avec le temps (en fait, la moyenne ne change pas avec le temps).

• Résumé

Si l’intégration est expliquée de manière purement mathématique, elle sera plus compliquée, et des cours de quantification ultérieurs seront impliqués. Nous faisons simplement une introduction simple au niveau de la compréhension du niveau 0, dans le but de mieux associer l’intégration aux applications réelles.

Pour partager, passez à la classe de quantification