Classificateur bayésien basé sur l'algorithme KNN
 0
0
 1951
1951
Classificateur bayésien basé sur l’algorithme KNN
Les bases théoriques de la conception des classificateurs pour la prise de décision de classification La théorie de décision de Bayes:
P{\displaystyle \omega _{i}}} est la probabilité de classement d’une donnée comme étant de classe i, en fonction de la formule de Bayes. On peut la représenter comme:
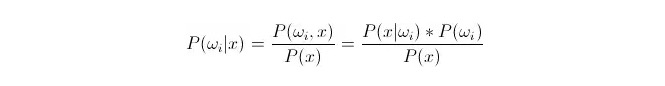
Parmi elles, P (x) {\displaystyle \mathrm {P} (x) }i) est appelée probabilité d’apparence ou probabilité conditionnelle; P (ω) {\displaystyle \mathrm {P} (ω) }i) est appelée probabilité antérieure, car elle n’est pas liée à l’expérience et peut être connue avant l’expérience.
Lors de la classification, on choisit la catégorie dans laquelle la probabilité de retrospective est la plus élevée (P). On compare chaque catégorie sous P. Lorsque P est petite, ωi est variable et x est fixe; on peut donc supprimer P sans y penser.
Donc cela se résume à calculer P (x) =*P ((ωi) est une question. La probabilité d’avance P ((ωi) est souhaitable, tant que la formation statistique se concentre sur la proportion de données qui apparaissent sous chaque classification.
Il est impossible de calculer directement la probabilité P (x < i) en fonction de l’ensemble d’entraînement. Il faut alors trouver la loi de distribution des données de l’ensemble d’entraînement pour obtenir P (x < i).
Voici une présentation de l’algorithme de voisinage k, en anglais KNN.
Nous allons adapter la distribution de ces données sous la catégorie ωi en fonction des données x1, x2…xn (dont chacune est de dimension m) de l’ensemble d’entraînement. Si x est un point quelconque dans l’espace de dimension m, comment calculer P (x) de ωi ?
On sait que, lorsque la quantité de données est suffisamment grande, on peut utiliser une approximation proportionnelle de la probabilité. On utilise ce principe pour trouver, autour du point x, les k points de l’échantillon les plus proches de la distance du point x, parmi lesquels certains sont de catégorie i. On calcule le volume V de la plus petite supersphère entourant ces k points de l’échantillon; on trouve également le nombre de Ni qui appartiennent à la catégorie ωi dans toutes les données de l’échantillon:
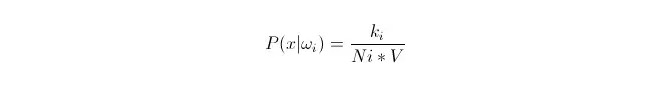
On peut voir que ce que nous avons calculé est en fait la densité de probabilité de classe conditionnelle au point x.
P (ωi) est égal à ? D’après la méthode ci-dessus, P ((ωi) = Ni/N 。 où N est le nombre total d’échantillons。 En plus, P (x) = k/N.*V), où k est le nombre de points d’échantillonnage entourant cette supersphère; N est le nombre total d’échantillons. Donc P (ωi 11:3x) peut être calculé: en introduisant cette formule, il est facile de trouver:
P(ωi|x)=ki/k
Dans une supersphère de la taille de V, nous avons entouré k échantillons, dont certains appartiennent à la classe i. Ainsi, nous déterminons le plus grand nombre d’échantillons entourés, et nous déterminons à quelle classe x devrait appartenir. C’est le classificateur conçu avec l’algorithme de proximité k.