Modélisation et analyse de la volatilité du Bitcoin basée sur le modèle ARMA-EGARCH

Récemment, j'ai fait une analyse sur la volatilité du Bitcoin, qui est verbale et spontanée. Je partage donc simplement une partie de ma compréhension et du code comme suit. Ma capacité est limitée et le code n'est pas très parfait. S'il y a une erreur, veuillez l'indiquer et la corriger directement.

1. Une brève description des séries chronologiques de la finance

La série temporelle de la finance est un ensemble de modèles de séries de processus stochastiques basés sur une variable observée dans la dimension temporelle. La variable est généralement le taux de rendement des actifs.

Ici, on suppose audacieusement que le taux de rendement du Bitcoin est conforme aux caractéristiques du taux de rendement des actifs financiers généraux, c'est-à-dire qu'il s'agit d'une série faiblement lisse, qui peut être démontrée par des tests de cohérence de plusieurs échantillons.

Préparations, bibliothèques d'importation, fonctions d'encapsulation

La configuration de l'environnement de recherche est terminée. La bibliothèque requise pour les calculs ultérieurs est importée ici. Comme elle est écrite de façon intermittente, elle peut être redondante. Veuillez la nettoyer vous-même.

Dans [1]:

'''
start: 2020-02-01 00:00:00
end: 2020-03-01 00:00:00
period: 1h
exchanges: [{"eid":"Huobi","currency":"BTC_USDT","stocks":0}]
'''
from __future__ import absolute_import, division, print_function
from fmz import * # Import all FMZ functions
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.lines as mlines
import seaborn as sns
import statsmodels.api as sm
import statsmodels.formula.api as smf
import statsmodels.tsa.api as smt
from statsmodels.graphics.api import qqplot
from statsmodels.stats.diagnostic import acorr_ljungbox as lb_test
from scipy import stats
from arch import arch_model
from datetime import timedelta
from itertools import product
from math import sqrt
from sklearn.metrics import r2_score, mean_absolute_error, mean_squared_error

task = VCtx(__doc__) # Initialization, verification of FMZ reading of historical data
print(exchange.GetAccount())

Extrait [1]: Le taux de change de la valeur de l'actif de l'entreprise est le taux de change de l'actif de l'entreprise.

    #### Encapsulate some of the functions, which will be used later. If there is a source, see the note

Dans [17]:

# Plot functions
def tsplot(y, y_2, lags=None, title='', figsize=(18, 8)):  # source code: https://tomaugspurger.github.io/modern-7-timeseries.html
    fig = plt.figure(figsize=figsize)
    layout = (2, 2)
    ts_ax   = plt.subplot2grid(layout, (0, 0))
    ts2_ax = plt.subplot2grid(layout, (0, 1))
    acf_ax  = plt.subplot2grid(layout, (1, 0))
    pacf_ax = plt.subplot2grid(layout, (1, 1))
    y.plot(ax=ts_ax)
    ts_ax.set_title(title)
    y_2.plot(ax=ts2_ax)
    smt.graphics.plot_acf(y, lags=lags, ax=acf_ax)
    smt.graphics.plot_pacf(y, lags=lags, ax=pacf_ax)
    [ax.set_xlim(0) for ax in [acf_ax, pacf_ax]]
    sns.despine()
    plt.tight_layout()
    return ts_ax, ts2_ax, acf_ax, pacf_ax

# Performance evaluation
def get_rmse(y, y_hat):
    mse = np.mean((y - y_hat)**2)
    return np.sqrt(mse)

def get_mape(y, y_hat):
    perc_err = (100*(y - y_hat))/y
    return np.mean(abs(perc_err))

def get_mase(y, y_hat):
    abs_err = abs(y - y_hat)
    dsum=sum(abs(y[1:] - y_hat[1:]))
    t = len(y)
    denom = (1/(t - 1))* dsum
    return np.mean(abs_err/denom)

def mae(observation, forecast):    
    error = mean_absolute_error(observation, forecast)
    print('Mean Absolute Error (MAE): {:.3g}'.format(error))
    return error

def mape(observation, forecast): 
    observation, forecast = np.array(observation), np.array(forecast)
    # Might encounter division by zero error when observation is zero
    error = np.mean(np.abs((observation - forecast) / observation)) * 100
    print('Mean Absolute Percentage Error (MAPE): {:.3g}'.format(error))
    return error

def rmse(observation, forecast):
    error = sqrt(mean_squared_error(observation, forecast))
    print('Root Mean Square Error (RMSE): {:.3g}'.format(error))
    return error

def evaluate(pd_dataframe, observation, forecast):
    first_valid_date = pd_dataframe[forecast].first_valid_index()
    mae_error = mae(pd_dataframe[observation].loc[first_valid_date:, ], pd_dataframe[forecast].loc[first_valid_date:, ])
    mape_error = mape(pd_dataframe[observation].loc[first_valid_date:, ], pd_dataframe[forecast].loc[first_valid_date:, ])
    rmse_error = rmse(pd_dataframe[observation].loc[first_valid_date:, ], pd_dataframe[forecast].loc[first_valid_date:, ]) 

    ax = pd_dataframe.loc[:, [observation, forecast]].plot(figsize=(18,5))
    ax.xaxis.label.set_visible(False)
    return

1-2. Commençons par une brève compréhension des données historiques de Bitcoin

D'un point de vue statistique, nous pouvons jeter un coup d'œil à certaines caractéristiques des données de Bitcoin. En prenant comme exemple la description des données de l'année écoulée, le taux de rendement est calculé de manière simple, c'est-à-dire que le prix de clôture est soustrait logarithmiquement. La formule est la suivante: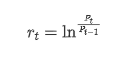

Dans [3]:

df = get_bars('huobi.btc_usdt', '1d', count=10000, start='2019-01-01')
btc_year = pd.DataFrame(df['close'],dtype=np.float)
btc_year.index.name = 'date'
btc_year.index = pd.to_datetime(btc_year.index)
btc_year['log_price'] = np.log(btc_year['close'])
btc_year['log_return'] = btc_year['log_price'] - btc_year['log_price'].shift(1)
btc_year['log_return_100x'] = np.multiply(btc_year['log_return'], 100)

btc_year_test = pd.DataFrame(btc_year['log_return'].dropna(), dtype=np.float)
btc_year_test.index.name = 'date'
mean = btc_year_test.mean()
std = btc_year_test.std()
normal_result = pd.DataFrame(index=['Mean Value', 'Std Value', 'Skewness Value','Kurtosis Value'], columns=['model value'])
normal_result['model value']['Mean Value'] = ('%.4f'% mean[0])
normal_result['model value']['Std Value'] = ('%.4f'% std[0])
normal_result['model value']['Skewness Value'] = ('%.4f'% btc_year_test.skew())
normal_result['model value']['Kurtosis Value'] = ('%.4f'% btc_year_test.kurt())
normal_result

Extrait [3]: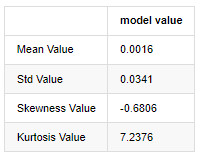

La caractéristique des queues de graisse épaisse est que plus l'échelle de temps est courte, plus la caractéristique est significative.

En prenant comme exemple les données quotidiennes du prix de clôture du 1er janvier 2019 à nos jours, nous faisons une analyse descriptive de son taux de rendement logarithmique, et on peut voir que la série de taux de rendement simple de Bitcoin ne se conforme pas à la distribution normale, et qu'elle a la caractéristique évidente de queues de graisse épaisse.

La valeur moyenne de la séquence est de 0,0016, l'écart-type est de 0,0341, l'asymétrie est de -0,6819 et la kurtosis est de 7,2243, ce qui est beaucoup plus élevé que la distribution normale et présente la caractéristique de queues de graisse épaisse.

Dans [4]:

fig = plt.figure(figsize=(4,4))
ax = fig.add_subplot(111)
fig = qqplot(btc_year_test['log_return'], line='q', ax=ax, fit=True)

Extrait [4]:

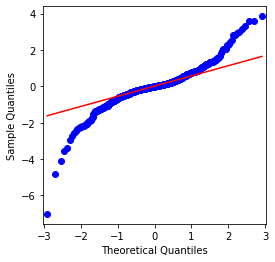
On peut voir que le graphique QQ est parfait, et la série de retour logarithmique pour Bitcoin ne se conforme pas à une distribution normale des résultats, et il a une caractéristique évidente de queues de graisse épaisse.

Ensuite, examinons l'effet d'agrégation de la volatilité, c'est-à-dire que les séries chronologiques financières sont souvent accompagnées d'une plus grande volatilité après une plus grande volatilité, tandis qu'une volatilité plus faible est généralement suivie d'une volatilité plus faible.

Le regroupement de la volatilité reflète les effets de rétroaction positifs et négatifs de la volatilité et est fortement corrélé avec les caractéristiques de la queue grasse.

Dans [5]:

df = get_bars('huobi.btc_usdt', '1d', count=50000, start='2006-01-01')
btc_year = pd.DataFrame(df['close'],dtype=np.float)
btc_year.index.name = 'date'
btc_year.index = pd.to_datetime(btc_year.index)
btc_year['log_price'] = np.log(btc_year['close'])
btc_year['log_return'] = btc_year['log_price'] - btc_year['log_price'].shift(1)
btc_year['log_return_100x'] = np.multiply(btc_year['log_return'], 100)

btc_year_test = pd.DataFrame(btc_year['log_return'].dropna(), dtype=np.float)
btc_year_test.index.name = 'date'
sns.mpl.rcParams['figure.figsize'] = (18, 4)  # Volatility
ax1 = btc_year_test['log_return'].plot()
ax1.xaxis.label.set_visible(False)

Extrait [5]:

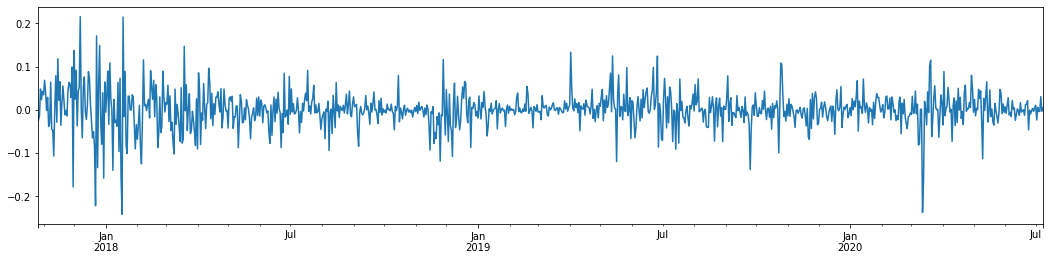
En prenant le taux logarithmique quotidien de rendement du Bitcoin au cours des 3 dernières années et en le traçant, le phénomène de regroupement de la volatilité peut être clairement vu. Après le marché haussier du Bitcoin en 2018, il était en position stable pendant la majeure partie du temps. Comme nous pouvons le voir à l'extrême droite, en mars 2020, alors que les marchés financiers mondiaux tombaient, il y avait aussi une course à la liquidité du Bitcoin, avec des rendements en chute rapide de près de 40% en une journée, avec de fortes oscillations négatives.

En un mot, d'après l'observation intuitive, nous pouvons voir qu'une grande fluctuation sera suivie d'une fluctuation dense avec une grande probabilité, qui est également l'effet d'agrégation de la volatilité.

1-3. Préparation des données

Pour préparer l'ensemble d'échantillons d'entraînement, nous établissons d'abord un échantillon de référence, dans lequel le taux de rendement logarithmique est l'équivalent de la volatilité observée.

La méthode de rééchantillonnage est basée sur des données horaires, la formule étant la suivante: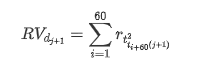

Dans [4]:

count_num = 100000
start_date = '2020-03-01'

df = get_bars('huobi.btc_usdt', '1m', count=50000, start='2020-02-13')  # Take the minute data
kline_1m = pd.DataFrame(df['close'], dtype=np.float)
kline_1m.index.name = 'date'
kline_1m['log_price'] = np.log(kline_1m['close'])
kline_1m['return'] = kline_1m['close'].pct_change().dropna()
kline_1m['log_return'] = kline_1m['log_price'] - kline_1m['log_price'].shift(1)

kline_1m['squared_log_return'] = np.power(kline_1m['log_return'], 2)

kline_1m['return_100x'] = np.multiply(kline_1m['return'], 100)
kline_1m['log_return_100x'] = np.multiply(kline_1m['log_return'], 100)  # Enlarge 100 times

df = get_bars('huobi.btc_usdt', '1h', count=860, start='2020-02-13')  # Take the hour data
kline_all = pd.DataFrame(df['close'], dtype=np.float)
kline_all.index.name = 'date'
kline_all['log_price'] = np.log(kline_all['close'])  # Calculate daily logarithmic rate of return
kline_all['return'] = kline_all['log_price'].pct_change().dropna()
kline_all['log_return'] = kline_all['log_price'] - kline_all['log_price'].shift(1)  # Calculate logarithmic rate of return
kline_all['squared_log_return'] = np.power(kline_all['log_return'], 2)  # The exponential square of logarithmic daily rate of return

kline_all['return_100x'] = np.multiply(kline_all['return'], 100)
kline_all['log_return_100x'] = np.multiply(kline_all['log_return'], 100)  # Enlarge 100 times

kline_all['realized_variance_1_hour'] = kline_1m.loc[:, 'squared_log_return'].resample('h', closed='left', label='left').sum().copy()  # Resampling to days
kline_all['realized_volatility_1_hour'] = np.sqrt(kline_all['realized_variance_1_hour'])  # Volatility of variance derivation

kline_all = kline_all[4:-29] # Remove the last line because it is missing
kline_all.head(3)

Extrait [4]: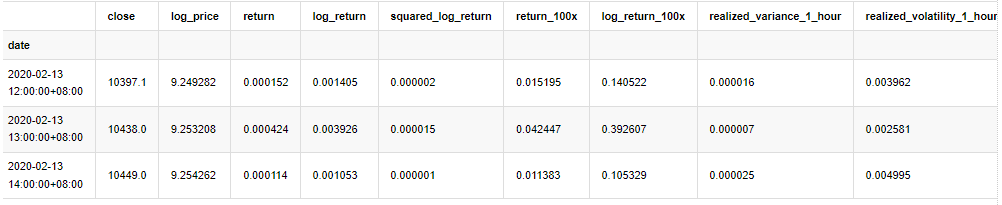

Préparer les données en dehors de l'échantillon de la même manière

Dans [5]:

# Prepare the data outside the sample with realized daily volatility
df = get_bars('huobi.btc_usdt', '1m', count=50000, start='2020-02-13')  # Take the minute data
kline_1m = pd.DataFrame(df['close'], dtype=np.float)
kline_1m.index.name = 'date'
kline_1m['log_price'] = np.log(kline_1m['close'])
kline_1m['log_return'] = kline_1m['log_price'] - kline_1m['log_price'].shift(1)
kline_1m['log_return_100x'] = np.multiply(kline_1m['log_return'], 100)  # Enlarge 100 times
kline_1m['squared_log_return'] = np.power(kline_1m['log_return_100x'], 2)
kline_1m#.tail()
df = get_bars('huobi.btc_usdt', '1h', count=860, start='2020-02-13')  # Take the hour data
kline_test = pd.DataFrame(df['close'], dtype=np.float)
kline_test.index.name = 'date'
kline_test['log_price'] = np.log(kline_test['close'])  # Calculate daily logarithmic rate of return
kline_test['log_return'] = kline_test['log_price'] - kline_test['log_price'].shift(1)  # Calculate logarithmic rate of return
kline_test['log_return_100x'] = np.multiply(kline_test['log_return'], 100)  # Enlarge 100 times
kline_test['squared_log_return'] = np.power(kline_test['log_return_100x'], 2)  # The exponential square of logarithmic daily rate of return
kline_test['realized_variance_1_hour'] = kline_1m.loc[:, 'squared_log_return'].resample('h', closed='left', label='left').sum()  # Resampling to days
kline_test['realized_volatility_1_hour'] = np.sqrt(kline_test['realized_variance_1_hour'])  # Volatility of variance derivation
kline_test = kline_test[4:-2]

Afin de comprendre les données de base de l'échantillon, une analyse descriptive simple est effectuée comme suit:

Dans [9]:

line_test = pd.DataFrame(kline_train['log_return'].dropna(), dtype=np.float)
line_test.index.name = 'date'

mean = line_test.mean()  # Calculate mean value and standard deviation
std = line_test.std()

line_test.sort_values(by = 'log_return', inplace = True)  # Resort
s_r = line_test.reset_index(drop = False)  # After resorting, update index
s_r['p'] = (s_r.index - 0.5) / len(s_r)  # Calculate the percentile p(i)
s_r['q'] = (s_r['log_return'] - mean) / std  # Calculate the value of q

st = line_test.describe()
x1 ,y1 = 0.25, st['log_return']['25%']
x2 ,y2 = 0.75, st['log_return']['75%']

fig = plt.figure(figsize = (18,8))
layout = (2, 2)
ax1 = plt.subplot2grid(layout, (0, 0), colspan=2)# Plot the data distribution
ax2 = plt.subplot2grid(layout, (1, 0))# Plot histogram
ax3 = plt.subplot2grid(layout, (1, 1))# Draw the QQ chart, the straight line is the connection of the quarter digit, three-quarters digit, which is basically conforms to the normal distribution

ax1.scatter(line_test.index, line_test.values)
line_test.hist(bins=30,alpha = 0.5,ax = ax2)
line_test.plot(kind = 'kde', secondary_y=True,ax = ax2)
ax3.plot(s_r['p'],s_r['log_return'],'k.',alpha = 0.1)
ax3.plot([x1,x2],[y1,y2],'-r')
sns.despine()
plt.tight_layout()

À l'extérieur[9]:

En conséquence, il existe une aggregation évidente de la volatilité et un effet de levier dans le graphique des séries chronologiques des rendements logarithmiques.

L'écart dans le tableau de distribution des rendements logarithmiques est inférieur à 0, ce qui indique que les rendements dans l'échantillon sont légèrement négatifs et biaisés vers la droite.

L'écartement de la distribution des données est inférieur à 1, ce qui indique que les rendements dans l'échantillon sont légèrement positifs et légèrement biaisés vers la droite.

Maintenant que nous sommes arrivés à ce point, faisons un autre test statistique. Dans [7]:

line_test = pd.DataFrame(kline_all['log_return'].dropna(), dtype=np.float)
line_test.index.name = 'date'
mean = line_test.mean()
std = line_test.std()
normal_result = pd.DataFrame(index=['Mean Value', 'Std Value', 'Skewness Value','Kurtosis Value',
                                    'Ks Test Value','Ks Test P-value',
                                    'Jarque Bera Test','Jarque Bera Test P-value'],
                    columns=['model value'])
normal_result['model value']['Mean Value'] = ('%.4f'% mean[0])
normal_result['model value']['Std Value'] = ('%.4f'% std[0])
normal_result['model value']['Skewness Value'] = ('%.4f'% line_test.skew())
normal_result['model value']['Kurtosis Value'] = ('%.4f'% line_test.kurt())
normal_result['model value']['Ks Test Value'] = stats.kstest(line_test, 'norm', (mean, std))[0]
normal_result['model value']['Ks Test P-value'] = stats.kstest(line_test, 'norm', (mean, std))[1]
normal_result['model value']['Jarque Bera Test'] = stats.jarque_bera(line_test)[0]
normal_result['model value']['Jarque Bera Test P-value'] = stats.jarque_bera(line_test)[1]
normal_result

À l'extérieur[7]:

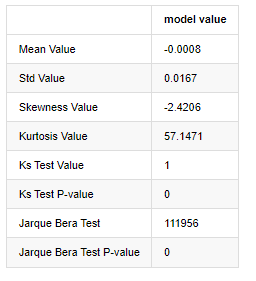
L'hypothèse initiale est caractérisée par une différence significative et une distribution normale. Si la valeur P est inférieure à la valeur critique du niveau de confiance de 0,05%, l'hypothèse initiale est rejetée.

On peut voir que la valeur de kurtosis est supérieure à 3, ce qui montre les caractéristiques des queues de graisse épaisse. Les valeurs P de KS et JB sont inférieures à l'intervalle de confiance. L'hypothèse de distribution normale est rejetée, ce qui prouve que le taux de rendement de BTC n'a pas les caractéristiques de la distribution normale, et l'étude empirique a les caractéristiques des queues de graisse épaisse.

1-4. Comparaison de la volatilité réalisée et de la volatilité observée

Nous combinons log_retour au carré (rendement logarithmique au carré) et variance réalisée (variance réalisée) pour les observations.

Dans [11]:

fig, ax = plt.subplots(figsize=(18, 6))
start = '2020-03-08 00:00:00+08:00'
end = '2020-03-20 00:00:00+08:00'

np.abs(kline_all['squared_log_return']).loc[start:end].plot(ax=ax,label='squared log return')
kline_all['realized_variance_1_hour'].loc[start:end].plot(ax=ax,label='realized variance')
plt.legend(loc='best')

À l'extérieur [11]:

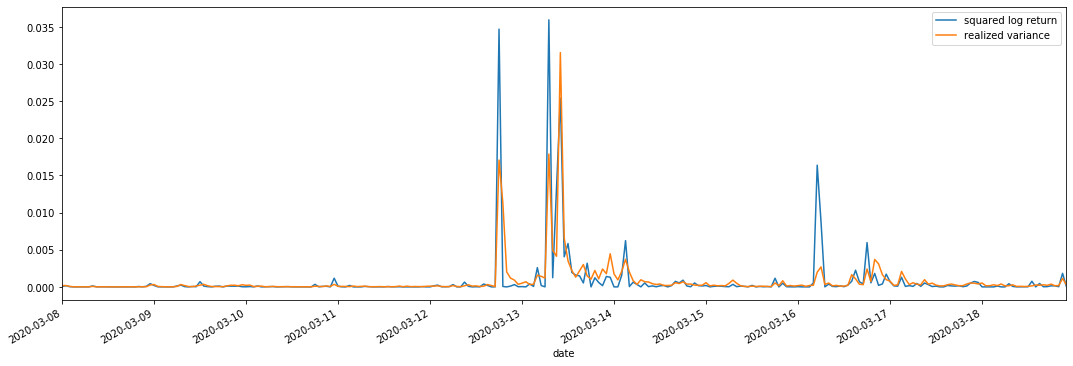
On peut voir que lorsque la plage de variance réalisée est plus grande, la volatilité de la plage de taux de rendement est également plus grande, et le taux de rendement réalisé est plus lisse.

D'un point de vue purement théorique, la RV est plus proche de la volatilité réelle, tandis que la volatilité à court terme est lissée en raison de la volatilité intraday appartient aux données du jour au lendemain, donc d'un point de vue d'observation, la volatilité intraday est plus appropriée pour une fréquence inférieure de volatilité du marché boursier.

2. Légèreté des séries chronologiques

Si c'est une série non stationnaire, elle doit être ajustée approximativement à une série stationnaire. La façon la plus courante est de faire le traitement des différences. Théoriquement, après plusieurs fois de différence, la série non stationnaire peut être approximée à une série stationnaire. Si la covariance de la série d'échantillons est stable, l'attente, la variance et la covariance de ses observations ne changeront pas avec le temps, ce qui indique que la série d'échantillons est plus pratique pour l'inférence dans l'analyse statistique.

Le test de la racine unitaire, à savoir le test ADF, est utilisé ici. Le test ADF utilise le test t pour observer la signification. En principe, si la série ne montre pas de tendance évidente, seuls les éléments constants sont conservés. Si la série a une tendance, l'équation de régression doit inclure à la fois les éléments constants et les éléments de tendance temporelle. En outre, les critères AIC et BIC peuvent être utilisés pour l'évaluation basée sur des critères d'information. Si la formule est requise, elle est la suivante: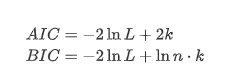

Dans [8]:

stable_test = kline_all['log_return']
adftest = sm.tsa.stattools.adfuller(np.array(stable_test), autolag='AIC')
adftest2 = sm.tsa.stattools.adfuller(np.array(stable_test), autolag='BIC')
output=pd.DataFrame(index=['ADF Statistic Test Value', "ADF P-value", "Lags", "Number of Observations",
                           "Critical Value(1%)","Critical Value(5%)","Critical Value(10%)"],
                    columns=['AIC','BIC'])
output['AIC']['ADF Statistic Test Value'] = adftest[0]
output['AIC']['ADF P-value'] = adftest[1]
output['AIC']['Lags'] = adftest[2]
output['AIC']['Number of Observations'] = adftest[3]
output['AIC']['Critical Value(1%)'] = adftest[4]['1%']
output['AIC']['Critical Value(5%)'] = adftest[4]['5%']
output['AIC']['Critical Value(10%)'] = adftest[4]['10%']
output['BIC']['ADF Statistic Test Value'] = adftest2[0]
output['BIC']['ADF P-value'] = adftest2[1]
output['BIC']['Lags'] = adftest2[2]
output['BIC']['Number of Observations'] = adftest2[3]
output['BIC']['Critical Value(1%)'] = adftest2[4]['1%']
output['BIC']['Critical Value(5%)'] = adftest2[4]['5%']
output['BIC']['Critical Value(10%)'] = adftest2[4]['10%']
output

À l'extérieur[8]: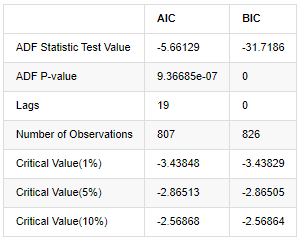

L'hypothèse initiale est qu'il n'y a pas de racine unitaire dans la série, c'est-à-dire que l'hypothèse alternative est que la série est stationnaire.

3. Identification du modèle et détermination de la commande

Pour établir l'équation de valeur moyenne, il est nécessaire de faire un test d'autocorrélation sur la séquence pour s'assurer que le terme d'erreur n'a pas d'autocorrélation.

Dans [19]:

tsplot(kline_all['log_return'], kline_all['log_return'], title='Log Return', lags=100)

Extrait [1]:

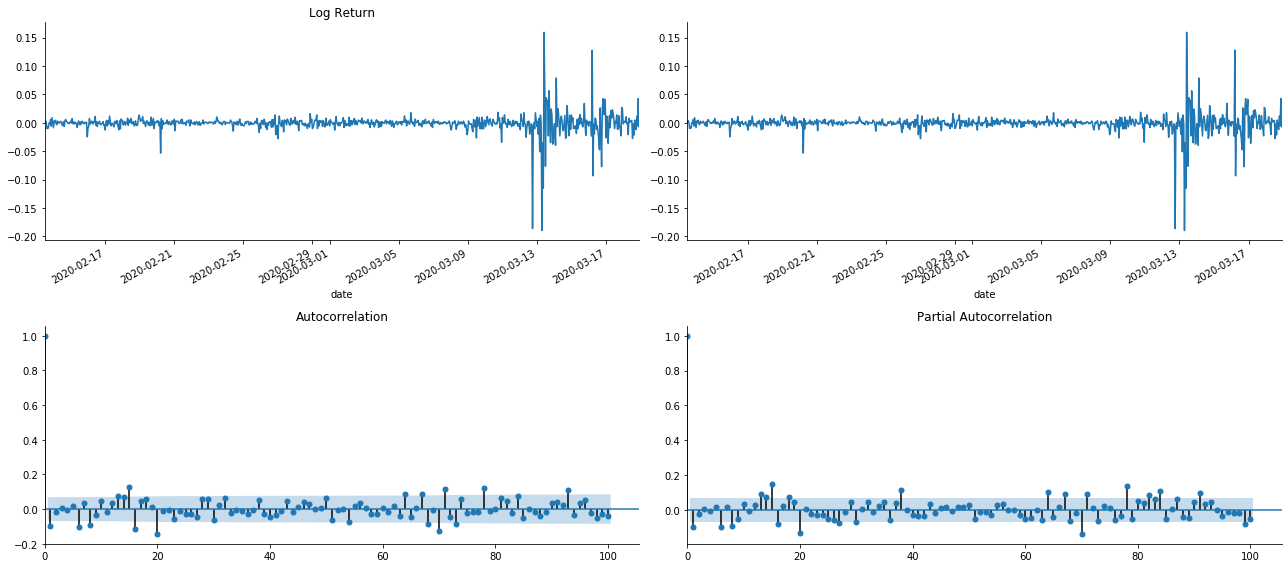
On peut voir que l'effet de troncation est parfait. À ce moment-là, cette image m'a donné une inspiration. Le marché est-il vraiment invalide? Afin de vérifier, nous allons faire une analyse d'autocorrélation sur la série de retour et déterminer l'ordre de retard du modèle.

Le coefficient de corrélation couramment utilisé est de mesurer la corrélation entre elle et elle-même, c'est-à-dire la corrélation entre r(t) et r (t-l) à un certain moment dans le passé: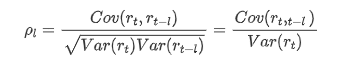

Ensuite, faisons un test quantitatif. L'hypothèse initiale est que tous les coefficients d'autocorrélation sont 0, c'est-à-dire qu'il n'y a pas d'autocorrélation dans la série.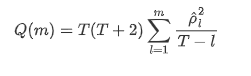

Dix coefficients d'autocorrélation ont été prélevés pour l'analyse, comme suit:

Dans [9]:

acf,q,p = sm.tsa.acf(kline_all['log_return'], nlags=15,unbiased=True,qstat = True, fft=False)  # Test 10 autocorrelation coefficients
output = pd.DataFrame(np.c_[range(1,16), acf[1:], q, p], columns=['lag', 'ACF', 'Q', 'P-value'])
output = output.set_index('lag')
output

À l'extérieur[9]: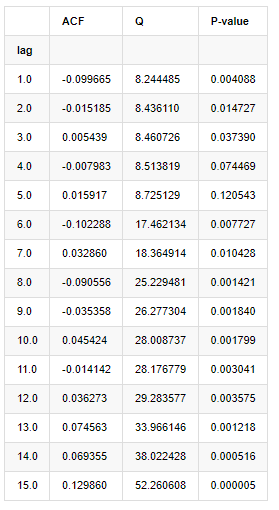

Selon la statistique de test Q et la valeur P, nous pouvons voir que la fonction d'autocorrélation ACF devient progressivement 0 après l'ordre 0. Les valeurs P des statistiques de test Q sont suffisamment petites pour rejeter l'hypothèse originale, donc il y a une autocorrélation dans la série.

4. modélisation ARMA

Les modèles AR et MA sont assez simples. Pour le dire simplement, Markdown est trop fatigué pour écrire des formules. Si vous êtes intéressé, veuillez les vérifier vous-même. Le modèle AR (Autorégression) est principalement utilisé pour modéliser les séries temporelles. Si la série a passé le test ACF, c'est-à-dire que le coefficient d'autocorrélation avec un intervalle de 1 est significatif, c'est-à-dire que les données à l'époque peuvent être utiles pour prédire le temps t.

Le modèle MA (mobilité moyenne) utilise l'interférence aléatoire ou la prédiction d'erreur des périodes q passées pour exprimer la valeur de prédiction actuelle de manière linéaire.

Pour décrire pleinement la structure dynamique des données, il est nécessaire d'augmenter l'ordre des modèles AR ou MA, mais ces paramètres rendront le calcul plus complexe.

Puisque les séries temporelles de prix sont généralement non stationnaires, et que l'effet d'optimisation de la méthode de différence sur la stationnalité a été discuté précédemment, le modèle ARIMA (p, d, q) (moyenne mobile autorégressive de somme) ajoute un traitement de différence d'ordre sur la base de l'application des modèles existants à la série.

En un mot, la seule différence entre le modèle ARIMA et le processus de construction du modèle ARMA est que si les résultats instables sont obtenus après l'analyse de la stationnalité, le modèle effectuera une différence quadratique à la série directement et effectuera ensuite le test de stationnalité, puis déterminera l'ordre p et q jusqu'à ce que la série soit stable.

Sélection de l'ordre

Ensuite, nous pouvons sélectionner l'ordre directement par le critère de l'information, ici nous essayons avec les diagrammes thermodynamiques de AIC et BIC.

Dans [10]:

def select_best_params():
    ps = range(0, 4)
    ds= range(1, 2)
    qs = range(0, 4)
    parameters = product(ps, ds, qs)
    parameters_list = list(parameters)

    p_min = 0
    d_min = 0
    q_min = 0
    p_max = 3
    d_max = 3
    q_max = 3

    results_aic = pd.DataFrame(index=['AR{}'.format(i) for i in range(p_min,p_max+1)],
                               columns=['MA{}'.format(i) for i in range(q_min,q_max+1)])
    results_bic = pd.DataFrame(index=['AR{}'.format(i) for i in range(p_min,p_max+1)],
                               columns=['MA{}'.format(i) for i in range(q_min,q_max+1)])
    
    best_params = []
    aic_results = []
    bic_results = []
    hqic_results = []
    best_aic = float("inf")
    best_bic = float("inf")
    best_hqic = float("inf")
    warnings.filterwarnings('ignore')
    for param in parameters_list:
        try:
            model = sm.tsa.SARIMAX(kline_all['log_price'], order=(param[0], param[1], param[2])).fit(disp=-1)
            results_aic.loc['AR{}'.format(param[0]), 'MA{}'.format(param[2])] = model.aic
            results_bic.loc['AR{}'.format(param[0]), 'MA{}'.format(param[2])] = model.bic
        except ValueError:
            continue    
           
        aic_results.append([param, model.aic])
        bic_results.append([param, model.bic])
        hqic_results.append([param, model.hqic])
    
    results_aic = results_aic[results_aic.columns].astype(float)
    results_bic = results_bic[results_bic.columns].astype(float)
    
    # Draw thermodynamic diagrams of AIC and BIC to find the best
    fig = plt.figure(figsize=(18, 9))
    layout = (2, 2)
    aic_ax = plt.subplot2grid(layout, (0, 0))
    bic_ax = plt.subplot2grid(layout, (0, 1))

    aic_ax = sns.heatmap(results_aic,mask=results_aic.isnull(),ax=aic_ax,cmap='OrRd',annot=True,fmt='.2f',);
    aic_ax.set_title('AIC');
    bic_ax = sns.heatmap(results_bic,mask=results_bic.isnull(),ax=bic_ax,cmap='OrRd',annot=True,fmt='.2f',);
    bic_ax.set_title('BIC');
    
    aic_df = pd.DataFrame(aic_results)
    aic_df.columns = ['params', 'aic']   
    best_params.append(aic_df.params[aic_df.aic.idxmin()])
    print('AIC best param: {}'.format(aic_df.params[aic_df.aic.idxmin()]))
    
    bic_df = pd.DataFrame(bic_results)
    bic_df.columns = ['params', 'bic']
    best_params.append(bic_df.params[bic_df.bic.idxmin()])
    print('BIC best param: {}'.format(bic_df.params[bic_df.bic.idxmin()]))
    
    hqic_df = pd.DataFrame(hqic_results)
    hqic_df.columns = ['params', 'hqic']
    best_params.append(hqic_df.params[hqic_df.hqic.idxmin()])
    print('HQIC best param: {}'.format(hqic_df.params[hqic_df.hqic.idxmin()]))

    for best_param in best_params:
        if best_params.count(best_param)>=2:
            print('Best Param Selected: {}'.format(best_param))
            return best_param 

best_param = select_best_params()

À l'extérieur [10]: Paramètre optimal de l'AIC: (0, 1, 1) Paramètre BIC le plus approprié: (0, 1, 1) Paramètres optimaux pour le HQIC: (0, 1, 1) Meilleur param sélectionné: (0, 1, 1)

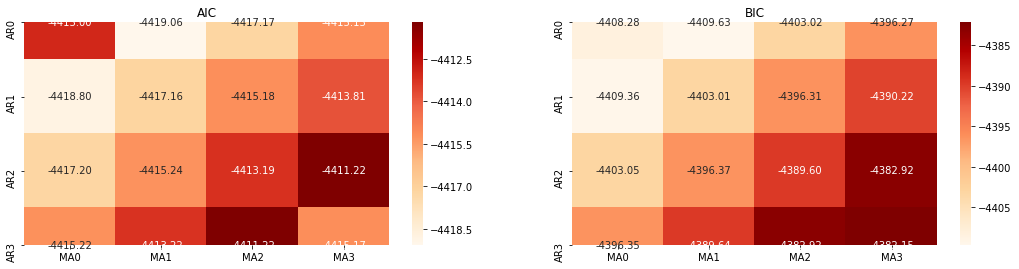
Il est évident que la combinaison optimale de paramètres de premier ordre pour le prix logarithmique est (0,1,1), ce qui est simple et direct. Le log_return (taux logarithmique de rendement) effectue la même opération. La valeur optimale AIC est (4,3), et la valeur optimale BIC est (0,1). La combinaison optimale de paramètres pour log_return (taux logarithmique de rendement) est donc (0,1).

4-2 Modélisation et correspondance ARMA

Les coefficients trimestriels ne sont pas requis, mais SARIMAX est plus riche en attributs, il a donc été décidé de choisir ce modèle pour la modélisation et de tracer par ailleurs une analyse descriptive comme suit:

Dans [11]:

params = (0, 0, 1)
training_model = smt.SARIMAX(endog=kline_all['log_return'], trend='c', order=params, seasonal_order=(0, 0, 0, 0))
model_results = training_model.fit(disp=False)
model_results.summary()

À l'extérieur [11]: Résultats du modèle d'espace d'État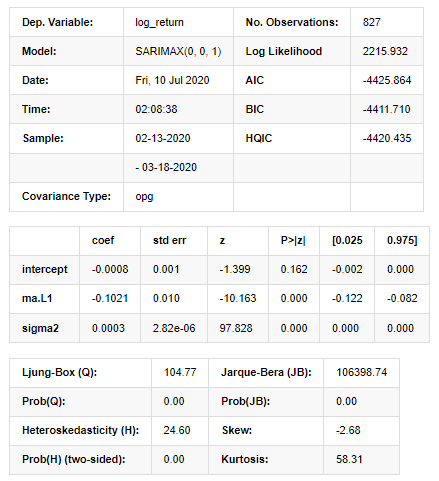

Avertissements: [1] Matrice de covariance calculée en utilisant le produit externe des gradients (étape complexe). Dans [27]:

model_results.plot_diagnostics(figsize=(18, 10));

Extrait[27]:

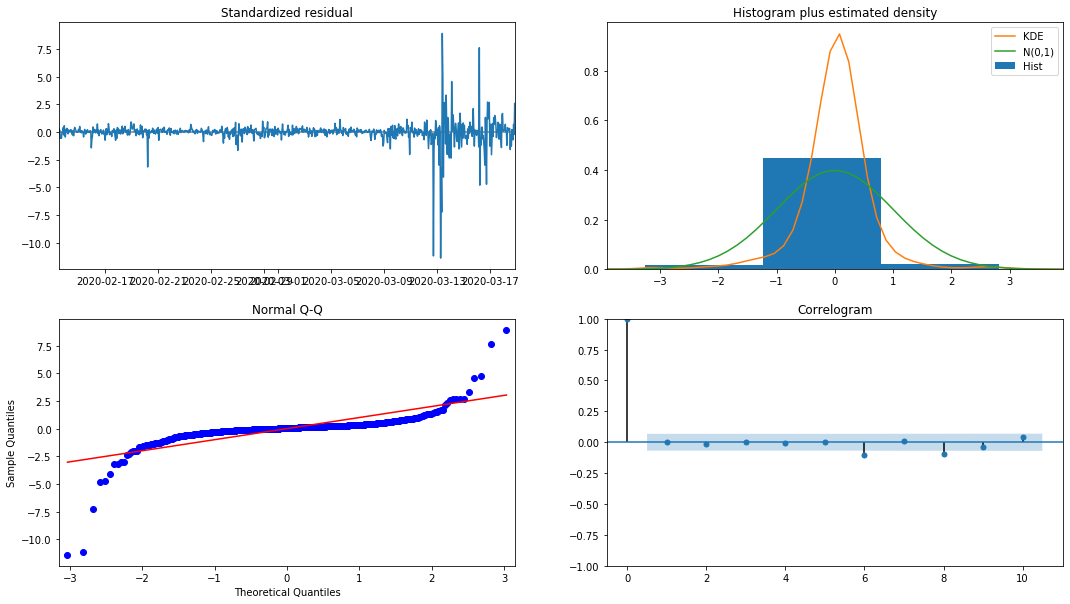
La densité de probabilité KDE dans l'histogramme est loin de la distribution normale N (0,1), ce qui indique que le résidu n'est pas une distribution normale.

Ensuite, après avoir dit cela, il faut encore tester si le modèle peut être utilisé.

4-3. Essai du modèle

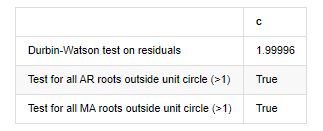
L'effet de correspondance du résiduel n'est pas idéal, nous avons donc effectué le test de Durbin Watson sur celui-ci. L'hypothèse initiale du test est que la séquence n'a pas d'autocorrélation et que la séquence d'hypothèse alternative est stationnaire. En outre, si les valeurs P des tests LB, JB et H sont inférieures à la valeur critique du niveau de confiance de 0,05%, l'hypothèse initiale sera rejetée.

Dans [12]:

het_method='breakvar'
norm_method='jarquebera'
sercor_method='ljungbox'

(het_stat, het_p) = model_results.test_heteroskedasticity(het_method)[0]
norm_stat, norm_p, skew, kurtosis = model_results.test_normality(norm_method)[0]

sercor_stat, sercor_p = model_results.test_serial_correlation(method=sercor_method)[0]
sercor_stat = sercor_stat[-1] # The last value of the maximum period
sercor_p = sercor_p[-1]

dw = sm.stats.stattools.durbin_watson(model_results.filter_results.standardized_forecasts_error[0, model_results.loglikelihood_burn:])

arroots_outside_unit_circle = np.all(np.abs(model_results.arroots) > 1)
maroots_outside_unit_circle = np.all(np.abs(model_results.maroots) > 1)

print('Test heteroskedasticity of residuals ({}): stat={:.3f}, p={:.3f}'.format(het_method, het_stat, het_p));
print('\nTest normality of residuals ({}): stat={:.3f}, p={:.3f}'.format(norm_method, norm_stat, norm_p));
print('\nTest serial correlation of residuals ({}): stat={:.3f}, p={:.3f}'.format(sercor_method, sercor_stat, sercor_p));
print('\nDurbin-Watson test on residuals: d={:.2f}\n\t(NB: 2 means no serial correlation, 0=pos, 4=neg)'.format(dw))
print('\nTest for all AR roots outside unit circle (>1): {}'.format(arroots_outside_unit_circle))
print('\nTest for all MA roots outside unit circle (>1): {}'.format(maroots_outside_unit_circle))

root_test=pd.DataFrame(index=['Durbin-Watson test on residuals','Test for all AR roots outside unit circle (>1)','Test for all MA roots outside unit circle (>1)'],columns=['c'])
root_test['c']['Durbin-Watson test on residuals']=dw
root_test['c']['Test for all AR roots outside unit circle (>1)']=arroots_outside_unit_circle
root_test['c']['Test for all MA roots outside unit circle (>1)']=maroots_outside_unit_circle
root_test

À l'extérieur [12]: Test d'hétéroskedasticité des résidus (breakvar): stat=24,598, p=0.000

Normalité de l'essai des résidus (jarquebera): stat=106398.739, p=0.000

Corrélation sérielle des résidus d'essai (caisse de test): stat=104,767, p=0.000

Test Durbin-Watson sur les résidus: d=2,00 (NB: 2 signifie aucune corrélation sérielle, 0=pos, 4=négatif)

Test pour toutes les racines AR situées en dehors du cercle unitaire (>1): Vrai

Test pour toutes les racines MA situées en dehors du cercle unitaire (>1): Vrai

Dans [13]:

kline_all['log_price_dif1'] = kline_all['log_price'].diff(1)
kline_all = kline_all[1:]
kline_train = kline_all

training_label = 'log_return'
training_ts = pd.DataFrame(kline_train[training_label], dtype=np.float)

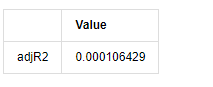
delta = model_results.fittedvalues - training_ts[training_label]
adjR = 1 - delta.var()/training_ts[training_label].var()
adjR_test=pd.DataFrame(index=['adjR2'],columns=['Value'])
adjR_test['Value']['adjR2']=adjR**2
adjR_test

À l'extérieur[13]:

Si la statistique du test de Durbin Watson est égale à 2, confirme que la série n'a pas de corrélation, et sa valeur statistique est répartie entre (0,4). Près de 0 signifie que la corrélation positive est élevée, tandis que près de 4 signifie que la corrélation négative est élevée. Ici, elle est approximativement égale à 2.

Dans [14]:

model_results.params

Extrait [1]: interception -0.000817 Le montant de l'aide est calculé en fonction de l'expérience acquise. sigma2 0,000275 dtype: flottant64

En résumé, ce paramètre de réglage d'ordre peut essentiellement répondre aux exigences de modélisation des séries temporelles et de modélisation de volatilité subséquente, mais l'effet de correspondance est tel quel.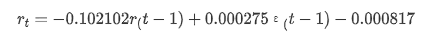

4-4. Prédiction du modèle

Ensuite, le modèle entraîné est assorti vers l'avant. statsmodels fournit des options statiques et dynamiques pour l'appariement et la prévision. La différence réside dans le fait que la valeur d'observation est utilisée dans la prochaine étape de la prévision, ou la valeur de prédiction générée dans l'étape précédente est utilisée de manière itérative.

Dans [37]:

start_date = '2020-02-28 12:00:00+08:00'
end_date = start_date 

pred_dy = model_results.get_prediction(start=start_date, dynamic=False)
pred_dy_ci = pred_dy.conf_int()

fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(18, 6))
ax.plot(kline_all['log_return'].loc[start_date:], label='Log Return', linestyle='-')
ax.plot(pred_dy.predicted_mean.loc[start_date:], label='Forecast Log Return', linestyle='--')
ax.fill_between(pred_dy_ci.index,pred_dy_ci.iloc[:, 0],pred_dy_ci.iloc[:, 1], color='g', alpha=.25)

plt.ylabel("BTC Log Return")
plt.legend(loc='best')
plt.tight_layout()
sns.despine()

Extrait [37]:

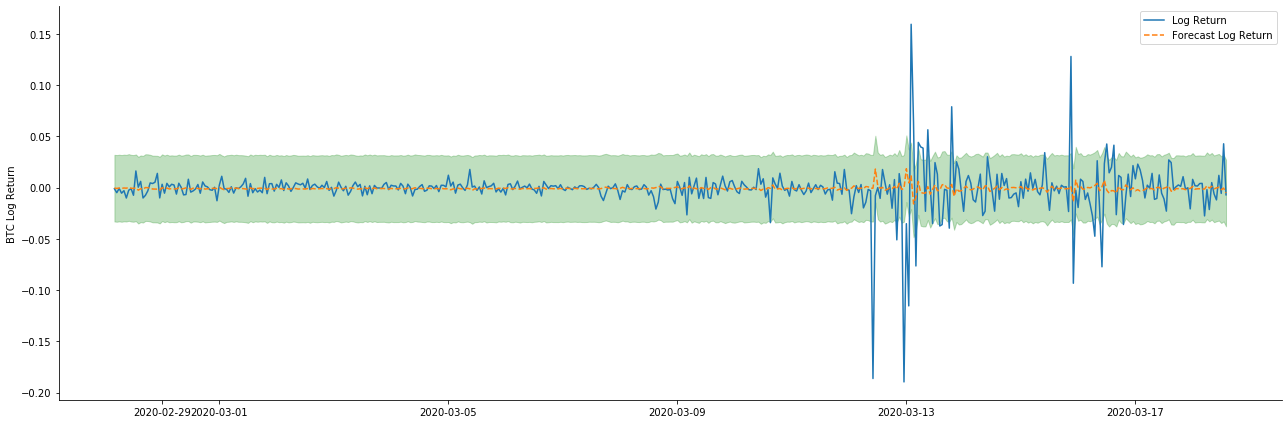
On constate que l'effet d'adaptation du mode statique sur l'échantillon est excellent, que les données d'échantillonnage peuvent être presque couvertes par un intervalle de confiance de 95% et que le mode dynamique est un peu hors de contrôle.

Voyons donc l'effet de correspondance des données en mode dynamique:

Dans [38]:

start_date = '2020-02-28 12:00:00+08:00'
end_date = start_date 

pred_dy = model_results.get_prediction(start=start_date, dynamic=True)
pred_dy_ci = pred_dy.conf_int()

fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(18, 6))
ax.plot(kline_all['log_return'].loc[start_date:], label='Log Return', linestyle='-')
ax.plot(pred_dy.predicted_mean.loc[start_date:], label='Forecast Log Return', linestyle='--')
ax.fill_between(pred_dy_ci.index,pred_dy_ci.iloc[:, 0],pred_dy_ci.iloc[:, 1], color='g', alpha=.25)

plt.ylabel("BTC Log Return")
plt.legend(loc='best')
plt.tight_layout()
sns.despine()

À l'extérieur[38]:

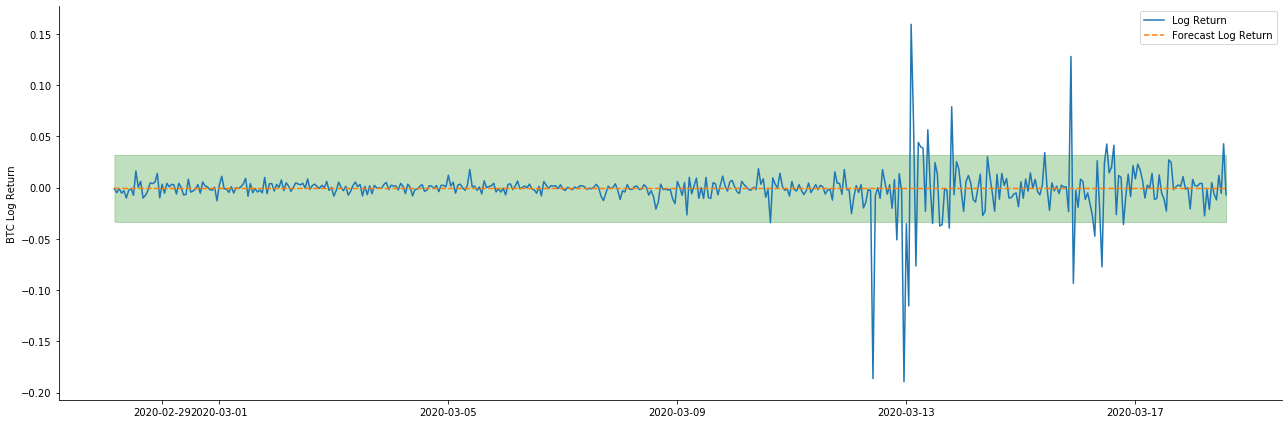
On constate que l'effet d'ajustement des deux modèles sur l'échantillon est excellent et que la valeur moyenne peut être presque couverte par l'intervalle de confiance de 95%, mais le modèle statique est évidemment plus approprié.

Dans [41]:

# Out-of-sample predicted data predict()
start_date = '2020-03-01 12:00:00+08:00'
end_date = '2020-03-20 23:00:00+08:00'
model = False

predict_step = 50
predicts_ARIMA_normal = model_results.get_prediction(start=start_date, dynamic=model, full_reports=True)
ci_normal = predicts_ARIMA_normal.conf_int().loc[start_date:]

predicts_ARIMA_normal_out = model_results.get_forecast(steps=predict_step, dynamic=model)
ci_normal_out = predicts_ARIMA_normal_out.conf_int().loc[start_date:end_date]

fig, ax = plt.subplots(figsize=(18,8))
kline_test.loc[start_date:end_date, 'log_return'].plot(ax=ax, label='Benchmark Log Return')

predicts_ARIMA_normal.predicted_mean.plot(ax=ax, style='g', label='In Sample Forecast')
ax.fill_between(ci_normal.index, ci_normal.iloc[:,0], ci_normal.iloc[:,1], color='g', alpha=0.1)

predicts_ARIMA_normal_out.predicted_mean.loc[:end_date].plot(ax=ax, style='r--', label='Out of Sample Forecast')
ax.fill_between(ci_normal_out.index, ci_normal_out.iloc[:,0], ci_normal_out.iloc[:,1], color='r', alpha=0.1)

plt.tight_layout()
plt.legend(loc='best')
sns.despine()

À l'extérieur[41]:

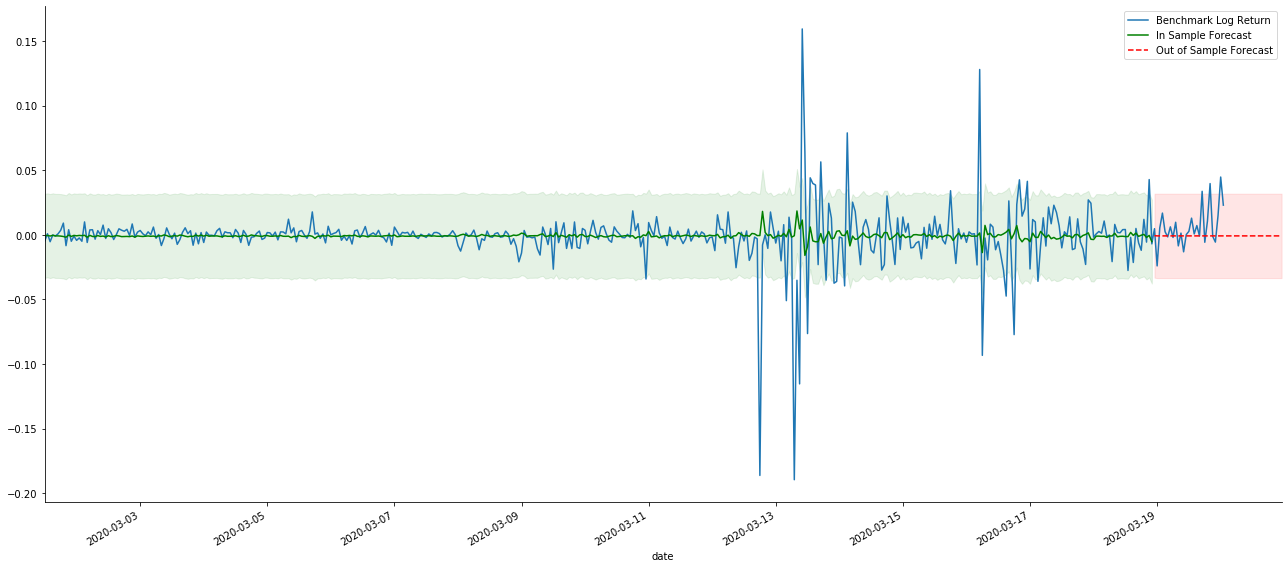
Parce que l'appariement des données dans l'échantillon est une prédiction progressive, lorsque la quantité d'informations dans l'échantillon est suffisante, le modèle statique est sujet au surappariement, tandis que le modèle dynamique manque de variables dépendantes fiables, et l'effet devient de plus en plus mauvais après l'itération.

Si nous inversons la prévision du taux de rendement à log_price (prix logarithmique), la correspondance est indiquée sur la figure ci-dessous:

Dans [42]:

params = (0, 1, 1)
mod = smt.SARIMAX(endog=kline_all['log_price'], trend='c', order=params, seasonal_order=(0, 0, 0, 0))
res = mod.fit(disp=False)

start_date = '2020-03-01 12:00:00+08:00'
end_date = '2020-03-15 23:00:00+08:00'

predicts_ARIMA_normal = res.get_prediction(start=start_date, dynamic=False, full_results=False)
predicts_ARIMA_dynamic = res.get_prediction(start=start_date, dynamic=True, full_results=False)

fig, ax = plt.subplots(figsize=(18,6))
kline_test.loc[start_date:end_date, 'log_price'].plot(ax=ax, label='Log Price')

predicts_ARIMA_normal.predicted_mean.loc[start_date:end_date].plot(ax=ax, style='r--', label='Normal Prediction')
ci_normal = predicts_ARIMA_normal.conf_int().loc[start_date:end_date]
ax.fill_between(ci_normal.index, ci_normal.iloc[:,0], ci_normal.iloc[:,1], color='r', alpha=0.1)

predicts_ARIMA_dynamic.predicted_mean.loc[start_date:end_date].plot(ax=ax, style='g', label='Dynamic Prediction')
ci_dynamic = predicts_ARIMA_dynamic.conf_int().loc[start_date:end_date]
ax.fill_between(ci_dynamic.index, ci_dynamic.iloc[:,0], ci_dynamic.iloc[:,1], color='g', alpha=0.1)

plt.tight_layout()
plt.legend(loc='best')
sns.despine()

À l'extérieur[42]:

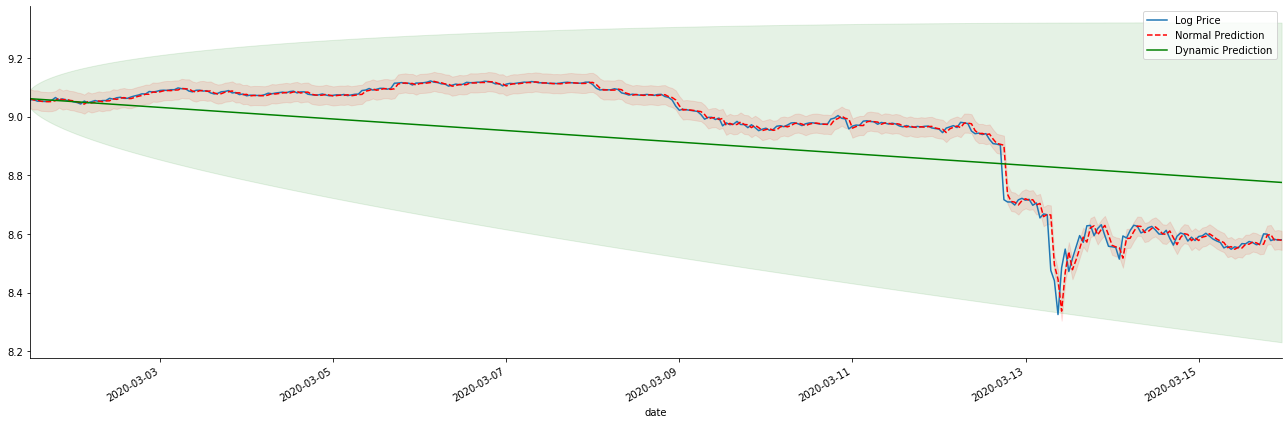
Il est facile de voir les avantages correspondants du modèle statique et la différence extrême entre le modèle dynamique et le modèle statique dans la prédiction à long terme. La ligne pointillée rouge et la plage rose... Vous ne pouvez pas dire que la prédiction de ce modèle est fausse. Après tout, il couvre complètement la tendance de la moyenne mobile, mais... est-ce significatif?

En fait, le modèle ARMA lui-même n'est pas faux, car le problème n'est pas le modèle lui-même, mais la logique objective des choses elles-mêmes. Le modèle de série temporelle ne peut être établi qu'en se basant sur la corrélation entre les observations précédentes et ultérieures. Par conséquent, il est impossible de modéliser la série de bruit blanc. Par conséquent, tout le travail précédent est basé sur une hypothèse audacieuse selon laquelle la série de taux de rendement de BTC ne peut pas être indépendante et identiquement distribuée.

En général, les séries de taux de rendement sont des séries de différence de martingale, ce qui signifie que le taux de rendement est imprévisible et que l'hypothèse de faible efficacité du marché correspondant est valable.

Cependant, la séquence résiduelle assortie est également une séquence de différence de martingale. La séquence de différence de martingale peut ne pas être indépendante et identiquement distribuée, mais la variance conditionnelle peut dépendre de la valeur passée, de sorte que l'autocorrélation de premier ordre a disparu, mais il y a encore une autocorrélation d'ordre supérieur, qui est également une condition préalable importante pour que la volatilité soit modélisée et observée.

Si une telle logique est vraie, alors la prémisse de la construction de divers modèles de volatilité est également vraie. Donc pour une série de taux de rendement, si un marché faiblement efficace est satisfait, alors la valeur moyenne doit être difficile à prédire, mais la variance est prévisible. Et l'ARMA apparié fournit une référence de série temporelle de qualité juste, alors la qualité détermine également la qualité de la prédiction de volatilité.

Enfin, évaluons simplement l'effet de la prédiction: avec l'erreur comme référence d'évaluation, les indicateurs à l'intérieur et à l'extérieur de l'échantillon sont:

Dans [15]:

start = '2020-02-14 00:00:00+08:00'
predicts_ARIMA_normal = model_results.get_prediction(dynamic=False)
predicts_ARIMA_dynamic = model_results.get_prediction(dynamic=True)
training_label = 'log_return'

compare_ARCH_X = pd.DataFrame()
compare_ARCH_X['Model'] = ['NORMAL','DYNAMIC']
compare_ARCH_X['RMSE'] = [rmse(predicts_ARIMA_normal.predicted_mean[1:], kline_test[training_label][:826]),
                          rmse(predicts_ARIMA_dynamic.predicted_mean[1:], kline_test[training_label][:826])]
compare_ARCH_X['MAPE'] = [mape(predicts_ARIMA_normal.predicted_mean[:50], kline_test[training_label][:50]),
                          mape(predicts_ARIMA_dynamic.predicted_mean[:50], kline_test[training_label][:50])]
compare_ARCH_X

Extrait [1]: L'erreur de la racine carrée moyenne (RMSE): 0,0184 Erreur de la racine moyenne carrée (RMSE): 0,0167 Faille moyenne en pourcentage absolu (MAPE): 2,25e+03 Faille moyenne en pourcentage absolu (MAPE): 395

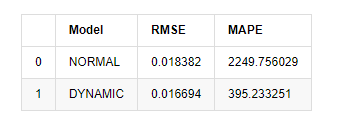
On peut voir que le modèle statique est légèrement meilleur que le modèle dynamique en termes de coïncidence d'erreur entre la valeur prédite et la valeur réelle. Il correspond bien au taux de rendement logarithmique du Bitcoin, ce qui est fondamentalement conforme aux attentes. La prédiction dynamique manque d'informations variables plus précises, et l'erreur est également amplifiée par l'itération, de sorte que l'effet de prédiction est faible.

Dans [18]:

predict_step = 50
predicts_ARIMA_normal_out = model_results.get_forecast(steps=predict_step, dynamic=False)
predicts_ARIMA_dynamic_out = model_results.get_forecast(steps=predict_step, dynamic=True)
testing_ts = kline_test
training_label = 'log_return'

compare_ARCH_X = pd.DataFrame()
compare_ARCH_X['Model'] = ['NORMAL','DYNAMIC']
compare_ARCH_X['RMSE'] = [get_rmse(predicts_ARIMA_normal_out.predicted_mean, testing_ts[training_label]),
                          get_rmse(predicts_ARIMA_dynamic_out.predicted_mean, testing_ts[training_label])]
compare_ARCH_X['MAPE'] = [get_mape(predicts_ARIMA_normal_out.predicted_mean, testing_ts[training_label]),
                          get_mape(predicts_ARIMA_dynamic_out.predicted_mean, testing_ts[training_label])]
compare_ARCH_X

À l'extérieur [1]:

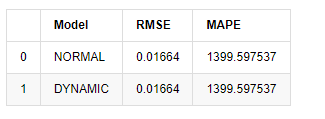
Étant donné que la prochaine prédiction en dehors de l'échantillon dépend des résultats de l'étape précédente, seul le modèle dynamique est efficace. Cependant, le défaut d'erreur à long terme du modèle dynamique entraîne une capacité de prédiction insuffisante du modèle global, de sorte que l'étape suivante est prévue au maximum.

En résumé, le modèle statique du modèle ARMA est adapté pour faire correspondre le taux de rendement intra-échantillon de Bitcoin. La prédiction à court terme du taux de rendement peut couvrir l'intervalle de confiance efficacement, mais la prédiction à long terme est très difficile, ce qui répond à la faible efficacité du marché.

5. effet ARCH

L'effet de modèle ARCH est la corrélation en série de la séquence d'hétéroscedasticité conditionnelle. Le test de mélange Ljung Box est utilisé pour tester la corrélation de la série carrée résiduelle pour déterminer s'il existe un effet ARCH. Si le test d'effet ARCH est passé, c'est-à-dire que la série a une hétéroscedasticité, l'étape suivante de la modélisation GARCH peut être effectuée pour estimer conjointement l'équation moyenne et l'équation de volatilité. Sinon, le modèle doit être optimisé et réajusté, comme le traitement différentiel ou la série réciproque.

Nous préparons quelques ensembles de données et variables globales ici:

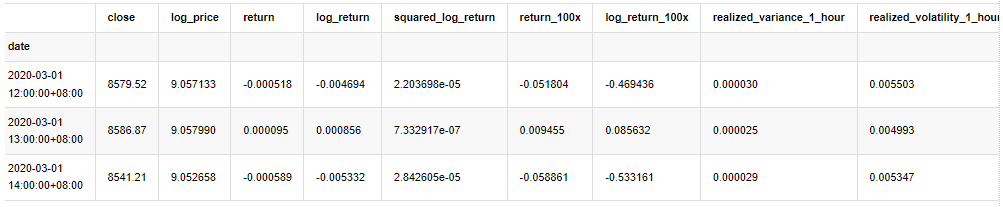
Dans [33]:

count_num = 100000
start_date = '2020-03-01'

df = get_bars('huobi.btc_usdt', '1m', count=count_num, start=start_date)  # Take the minute data
kline_1m = pd.DataFrame(df['close'], dtype=np.float)
kline_1m.index.name = 'date'
kline_1m['log_price'] = np.log(kline_1m['close'])
kline_1m['return'] = kline_1m['close'].pct_change().dropna()
kline_1m['log_return'] = kline_1m['log_price'] - kline_1m['log_price'].shift(1)

kline_1m['squared_log_return'] = np.power(kline_1m['log_return'], 2)

kline_1m['return_100x'] = np.multiply(kline_1m['return'], 100)
kline_1m['log_return_100x'] = np.multiply(kline_1m['log_return'], 100)  # Enlarge 100 times

df = get_bars('huobi.btc_usdt', '1h', count=count_num, start=start_date)  # Take the hour data
kline_test = pd.DataFrame(df['close'], dtype=np.float)
kline_test.index.name = 'date'
kline_test['log_price'] = np.log(kline_test['close'])  # Calculate the daily logarithmic rate of return
kline_test['return'] = kline_test['log_price'].pct_change().dropna()
kline_test['log_return'] = kline_test['log_price'] - kline_test['log_price'].shift(1)  # Calculate the logarithmic rate of return
kline_test['squared_log_return'] = np.power(kline_test['log_return'], 2)  # Exponential square of log daily return rate

kline_test['return_100x'] = np.multiply(kline_test['return'], 100)
kline_test['log_return_100x'] = np.multiply(kline_test['log_return'], 100)  # Enlarge 100 times

kline_test['realized_variance_1_hour'] = kline_1m.loc[:, 'squared_log_return'].resample('h', closed='left', label='left').sum().copy() # Resampling to days 
kline_test['realized_volatility_1_hour'] = np.sqrt(kline_test['realized_variance_1_hour'])  # Volatility of variance derivation

kline_test = kline_test[4:-2500]
kline_test.head(3)

À l'extérieur[33]:

Dans [22]:

cc = 3
model_p = 1
predict_lag = 30
label = 'log_return'

training_label = label
training_ts = pd.DataFrame(kline_test[training_label], dtype=np.float)

training_arch_label = label
training_arch = pd.DataFrame(kline_test[training_arch_label], dtype=np.float)

training_garch_label = label
training_garch = pd.DataFrame(kline_test[training_garch_label], dtype=np.float)

training_egarch_label = label
training_egarch = pd.DataFrame(kline_test[training_egarch_label], dtype=np.float)

training_arch.plot(figsize = (18,4))

Extrait[22]: Je suis en train d'essayer de trouver une solution.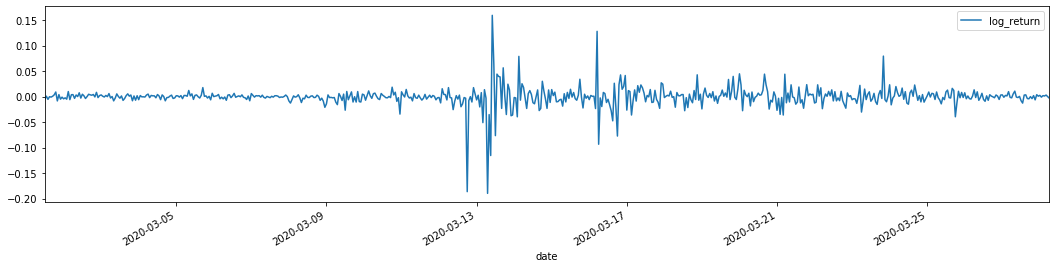

Les taux de retour logarithmique sont montrés ci-dessus. Ensuite, nous devons tester l'effet ARCH de l'échantillon. Nous établissons la série résiduelle dans l'échantillon basée sur ARMA. Certaines séries et la série carrée de résiduel et résiduel sont calculées en premier:

Dans [20]:

training_arma_model = smt.SARIMAX(endog=training_ts, trend='c', order=(0, 0, 1), seasonal_order=(0, 0, 0, 0))
arma_model_results = training_arma_model.fit(disp=False)
arma_model_results.summary()
training_arma_fitvalue = pd.DataFrame(arma_model_results.fittedvalues,dtype=np.float)
at = pd.merge(training_ts, training_arma_fitvalue, on='date')
at.columns = ['log_return', 'model_fit']
at['res'] = at['log_return'] - at['model_fit']
at['res2'] = np.square(at['res'])
at.head()

Extrait [1]:

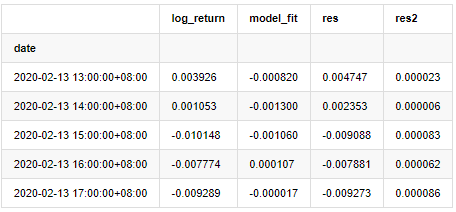
La série résiduelle de l'échantillon est ensuite tracée

Dans [69]:

fig, ax = plt.subplots(figsize=(18, 6))
ax1 = fig.add_subplot(2,1,1)
at['res'][1:].plot(ax=ax1,label='resid')
plt.legend(loc='best')

ax2 = fig.add_subplot(2,1,2)
at['res2'][1:].plot(ax=ax2,label='resid2')

plt.legend(loc='best')
plt.tight_layout()
sns.despine()

À l'extérieur [1]:

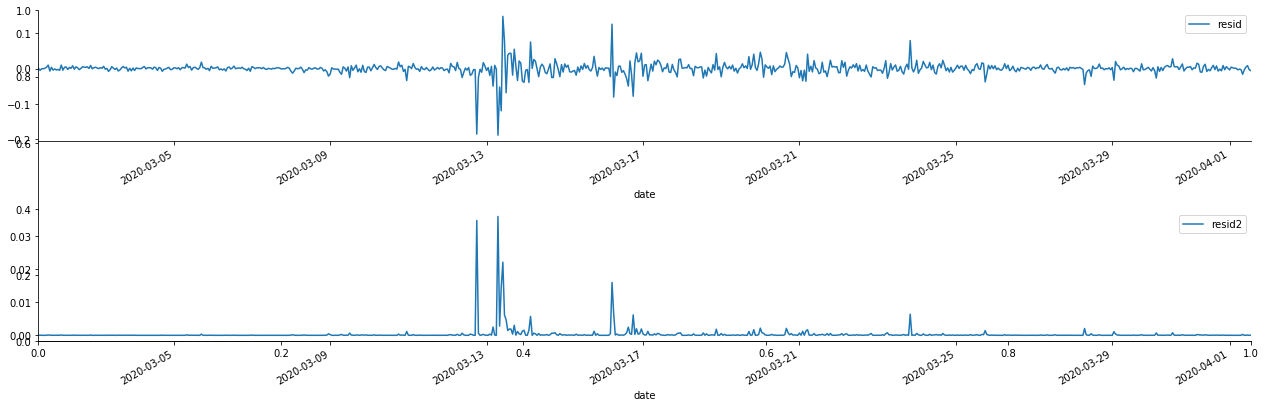
On peut voir que la série résiduelle a des caractéristiques d'agrégation évidentes, et on peut juger initialement que la série a un effet ARCH.

Dans [70]:

figure = plt.figure(figsize=(18,4))
ax1 = figure.add_subplot(111)
fig = sm.graphics.tsa.plot_acf(at['res2'],lags = 40, ax=ax1)

Extrait[70]:

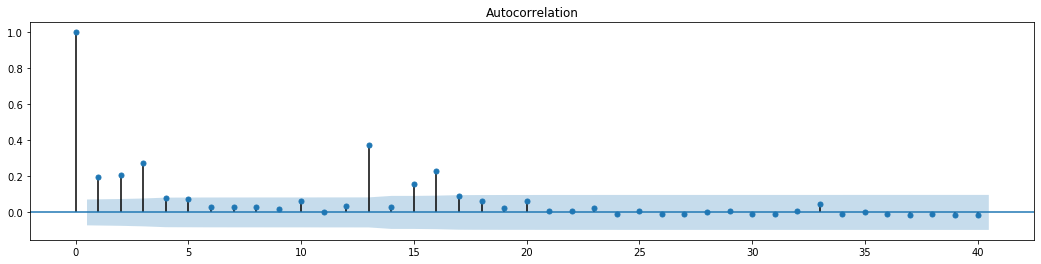
L'hypothèse initiale pour le test de mélange de séries est que la série n'a pas de corrélation. On peut voir que les valeurs P correspondantes des 20 premiers ordres de données sont inférieures à la valeur critique du niveau de confiance de 0,05%. Par conséquent, l'hypothèse initiale est rejetée, c'est-à-dire que le résidu de la série a l'effet ARCH. Le modèle de variance peut être établi à travers le modèle de type ARCH pour s'adapter à l'hétéroscedasticité de la série résiduelle et prédire davantage la volatilité.

6. modélisation GARCH

Avant d'effectuer la modélisation GARCH, nous devons nous occuper de la partie de la queue grasse de la série. Parce que le terme d'erreur de la série dans l'hypothèse doit être conforme à la distribution normale ou t distribution, et nous avons précédemment vérifié que la série de rendement a une distribution de queue grasse, nous devons donc décrire et compléter cette partie.

Dans la modélisation GARCH, l'élément d'erreur fournit les options de distribution normale, de distribution t, de distribution GED (distribution d'erreur généralisée) et de distribution t des étudiants faussés.

Relationnée

Plus de