ARMA-EGARCH मॉडल के आधार पर बिटकॉइन अस्थिरता का मॉडलिंग और विश्लेषण

हाल ही में, मैंने बिटकॉइन की अस्थिरता पर कुछ विश्लेषण किया है, जो शब्दहीन और सहज है। इसलिए मैं बस अपनी कुछ समझ और कोड को निम्नानुसार साझा करता हूं। मेरी क्षमता सीमित है, और कोड बहुत सही नहीं है। यदि कोई त्रुटि है, तो कृपया इसे इंगित करें और इसे सीधे सही करें।

1. वित्त की समय श्रृंखला का संक्षिप्त विवरण

वित्त की समय श्रृंखला समय आयाम में अवलोकन किए गए चर के आधार पर स्टोकास्टिक प्रक्रिया श्रृंखला मॉडल का एक सेट है। चर आमतौर पर परिसंपत्तियों की वापसी दर है। क्योंकि वापसी दर निवेश पैमाने से स्वतंत्र है और इसकी सांख्यिकीय प्रकृति है, यह अंतर्निहित वित्तीय परिसंपत्तियों के निवेश के अवसरों का विश्लेषण करने के लिए अधिक मूल्यवान है।

यहाँ, यह साहसपूर्वक माना जाता है कि बिटकॉइन की प्रतिफल दर सामान्य वित्तीय परिसंपत्तियों की प्रतिफल दर विशेषताओं के अनुरूप है, अर्थात, यह एक कमजोर चिकनी श्रृंखला है, जिसे कई नमूनों की स्थिरता परीक्षण द्वारा प्रदर्शित किया जा सकता है।

1-1. तैयारी, आयात पुस्तकालय, समाहित कार्य

अनुसंधान वातावरण का विन्यास पूरा हो गया है. बाद की गणनाओं के लिए आवश्यक पुस्तकालय यहाँ आयात किया गया है. चूंकि यह अंतराल से लिखा जाता है, इसलिए यह अनावश्यक हो सकता है. कृपया इसे स्वयं साफ करें.

में [1]:

'''
start: 2020-02-01 00:00:00
end: 2020-03-01 00:00:00
period: 1h
exchanges: [{"eid":"Huobi","currency":"BTC_USDT","stocks":0}]
'''
from __future__ import absolute_import, division, print_function
from fmz import * # Import all FMZ functions
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.lines as mlines
import seaborn as sns
import statsmodels.api as sm
import statsmodels.formula.api as smf
import statsmodels.tsa.api as smt
from statsmodels.graphics.api import qqplot
from statsmodels.stats.diagnostic import acorr_ljungbox as lb_test
from scipy import stats
from arch import arch_model
from datetime import timedelta
from itertools import product
from math import sqrt
from sklearn.metrics import r2_score, mean_absolute_error, mean_squared_error

task = VCtx(__doc__) # Initialization, verification of FMZ reading of historical data
print(exchange.GetAccount())

बाहर[1]: { बैलेंस : 10000.0, फ्रोजन बैलेंस : 0.0, स्टॉक : 0.0, फ्रोजन स्टॉक : 0.0}

    #### Encapsulate some of the functions, which will be used later. If there is a source, see the note

[17] मेंः

# Plot functions
def tsplot(y, y_2, lags=None, title='', figsize=(18, 8)):  # source code: https://tomaugspurger.github.io/modern-7-timeseries.html
    fig = plt.figure(figsize=figsize)
    layout = (2, 2)
    ts_ax   = plt.subplot2grid(layout, (0, 0))
    ts2_ax = plt.subplot2grid(layout, (0, 1))
    acf_ax  = plt.subplot2grid(layout, (1, 0))
    pacf_ax = plt.subplot2grid(layout, (1, 1))
    y.plot(ax=ts_ax)
    ts_ax.set_title(title)
    y_2.plot(ax=ts2_ax)
    smt.graphics.plot_acf(y, lags=lags, ax=acf_ax)
    smt.graphics.plot_pacf(y, lags=lags, ax=pacf_ax)
    [ax.set_xlim(0) for ax in [acf_ax, pacf_ax]]
    sns.despine()
    plt.tight_layout()
    return ts_ax, ts2_ax, acf_ax, pacf_ax

# Performance evaluation
def get_rmse(y, y_hat):
    mse = np.mean((y - y_hat)**2)
    return np.sqrt(mse)

def get_mape(y, y_hat):
    perc_err = (100*(y - y_hat))/y
    return np.mean(abs(perc_err))

def get_mase(y, y_hat):
    abs_err = abs(y - y_hat)
    dsum=sum(abs(y[1:] - y_hat[1:]))
    t = len(y)
    denom = (1/(t - 1))* dsum
    return np.mean(abs_err/denom)

def mae(observation, forecast):    
    error = mean_absolute_error(observation, forecast)
    print('Mean Absolute Error (MAE): {:.3g}'.format(error))
    return error

def mape(observation, forecast): 
    observation, forecast = np.array(observation), np.array(forecast)
    # Might encounter division by zero error when observation is zero
    error = np.mean(np.abs((observation - forecast) / observation)) * 100
    print('Mean Absolute Percentage Error (MAPE): {:.3g}'.format(error))
    return error

def rmse(observation, forecast):
    error = sqrt(mean_squared_error(observation, forecast))
    print('Root Mean Square Error (RMSE): {:.3g}'.format(error))
    return error

def evaluate(pd_dataframe, observation, forecast):
    first_valid_date = pd_dataframe[forecast].first_valid_index()
    mae_error = mae(pd_dataframe[observation].loc[first_valid_date:, ], pd_dataframe[forecast].loc[first_valid_date:, ])
    mape_error = mape(pd_dataframe[observation].loc[first_valid_date:, ], pd_dataframe[forecast].loc[first_valid_date:, ])
    rmse_error = rmse(pd_dataframe[observation].loc[first_valid_date:, ], pd_dataframe[forecast].loc[first_valid_date:, ]) 

    ax = pd_dataframe.loc[:, [observation, forecast]].plot(figsize=(18,5))
    ax.xaxis.label.set_visible(False)
    return

आइए बिटकॉइन के ऐतिहासिक आंकड़ों की संक्षिप्त समझ के साथ शुरू करें

सांख्यिकीय दृष्टिकोण से, हम बिटकॉइन की कुछ डेटा विशेषताओं पर एक नज़र डाल सकते हैं। पिछले वर्ष के डेटा विवरण को उदाहरण के रूप में लेते हुए, रिटर्न दर की गणना सरल तरीके से की जाती है, अर्थात समापन मूल्य को लघुगणकीय रूप से घटाया जाता है। सूत्र निम्नानुसार हैः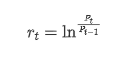

[3] मेंः

df = get_bars('huobi.btc_usdt', '1d', count=10000, start='2019-01-01')
btc_year = pd.DataFrame(df['close'],dtype=np.float)
btc_year.index.name = 'date'
btc_year.index = pd.to_datetime(btc_year.index)
btc_year['log_price'] = np.log(btc_year['close'])
btc_year['log_return'] = btc_year['log_price'] - btc_year['log_price'].shift(1)
btc_year['log_return_100x'] = np.multiply(btc_year['log_return'], 100)

btc_year_test = pd.DataFrame(btc_year['log_return'].dropna(), dtype=np.float)
btc_year_test.index.name = 'date'
mean = btc_year_test.mean()
std = btc_year_test.std()
normal_result = pd.DataFrame(index=['Mean Value', 'Std Value', 'Skewness Value','Kurtosis Value'], columns=['model value'])
normal_result['model value']['Mean Value'] = ('%.4f'% mean[0])
normal_result['model value']['Std Value'] = ('%.4f'% std[0])
normal_result['model value']['Skewness Value'] = ('%.4f'% btc_year_test.skew())
normal_result['model value']['Kurtosis Value'] = ('%.4f'% btc_year_test.kurt())
normal_result

बाहर[3]: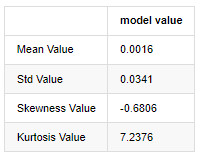

मोटी वसा वाली पूंछों की विशेषता यह है कि समय का पैमाना जितना छोटा होता है, वैशिष्ट्य उतना ही महत्वपूर्ण होता है। डेटा आवृत्ति में वृद्धि के साथ कर्टोसिस बढ़ेगा, और उच्च आवृत्ति वाले डेटा में यह विशेषता बहुत स्पष्ट होगी।

उदाहरण के तौर पर 1 जनवरी 2019 से लेकर आज तक के दैनिक समापन मूल्य के आंकड़ों को लेते हुए, हम इसकी लघुगणकीय प्रतिफल दर का वर्णनात्मक विश्लेषण करते हैं, और यह देखा जा सकता है कि बिटकॉइन की सरल प्रतिफल दर श्रृंखला सामान्य वितरण के अनुरूप नहीं है, और इसमें मोटी वसा की पूंछ की स्पष्ट विशेषता है।

क्रम का औसत मान 0.0016, मानक विचलन 0.0341, तिरछापन -0.6819 और कर्टोसिस 7.2243 है, जो सामान्य वितरण से बहुत अधिक है और इसमें मोटी वसा वाली पूंछ की विशेषता है। बिटकॉइन की सरल रिटर्न दर की सामान्यता को QQ चार्ट के साथ मापा और परीक्षण किया जाता है, इस प्रकारः

[4] मेंः

fig = plt.figure(figsize=(4,4))
ax = fig.add_subplot(111)
fig = qqplot(btc_year_test['log_return'], line='q', ax=ax, fit=True)

बाहर[4]:

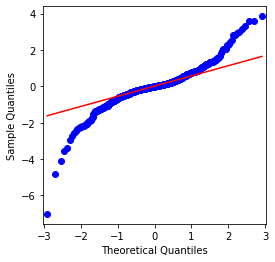
यह देखा जा सकता है कि QQ चार्ट सही है, और बिटकॉइन के लिए लघुगणकीय रिटर्न श्रृंखला परिणामों से सामान्य वितरण के अनुरूप नहीं है, और इसमें मोटी वसा पूंछ की स्पष्ट विशेषता है।

इसके बाद, चलिए अस्थिरता संचयन प्रभाव पर एक नज़र डालते हैं, अर्थात वित्तीय समय श्रृंखलाएं अक्सर अधिक अस्थिरता के बाद अधिक अस्थिरता के साथ होती हैं, जबकि कम अस्थिरता आमतौर पर कम अस्थिरता के बाद होती है।

अस्थिरता क्लस्टरिंग अस्थिरता के सकारात्मक और नकारात्मक प्रतिक्रिया प्रभावों को दर्शाता है और यह वसा पूंछ विशेषताओं के साथ अत्यधिक सहसंबद्ध है। अर्थशास्त्र में, इसका तात्पर्य यह है कि अस्थिरता की समय श्रृंखला ऑटो-संबद्ध हो सकती है, अर्थात, वर्तमान अवधि की अस्थिरता का पिछले अवधि, दूसरी पिछली अवधि या यहां तक कि तीसरी पिछली अवधि के साथ कुछ संबंध हो सकता है।

[5] मेंः

df = get_bars('huobi.btc_usdt', '1d', count=50000, start='2006-01-01')
btc_year = pd.DataFrame(df['close'],dtype=np.float)
btc_year.index.name = 'date'
btc_year.index = pd.to_datetime(btc_year.index)
btc_year['log_price'] = np.log(btc_year['close'])
btc_year['log_return'] = btc_year['log_price'] - btc_year['log_price'].shift(1)
btc_year['log_return_100x'] = np.multiply(btc_year['log_return'], 100)

btc_year_test = pd.DataFrame(btc_year['log_return'].dropna(), dtype=np.float)
btc_year_test.index.name = 'date'
sns.mpl.rcParams['figure.figsize'] = (18, 4)  # Volatility
ax1 = btc_year_test['log_return'].plot()
ax1.xaxis.label.set_visible(False)

बाहर[5]:

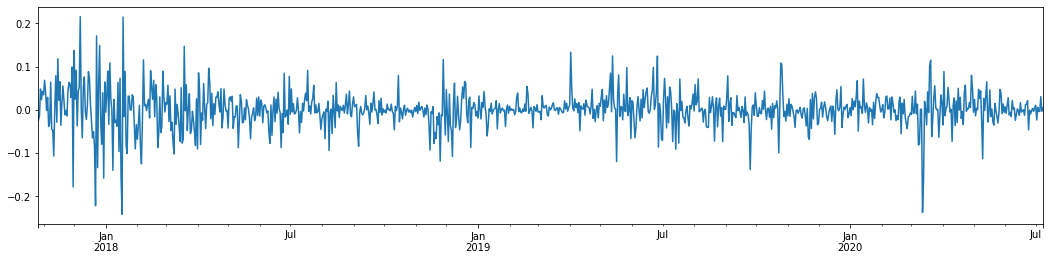
पिछले 3 वर्षों में बिटकॉइन की दैनिक लघुगणकीय प्रतिफल दर को लेते हुए और इसे प्लॉट करते हुए, अस्थिरता क्लस्टरिंग की घटना को स्पष्ट रूप से देखा जा सकता है। 2018 में बिटकॉइन में बुल मार्केट के बाद, यह अधिकांश समय के लिए स्थिर रुख में था। जैसा कि हम सबसे दाईं ओर देख सकते हैं, मार्च 2020 में, वैश्विक वित्तीय बाजारों में गिरावट के साथ, बिटकॉइन तरलता पर भी एक रन था, एक दिन में लगभग 40% की गिरावट के साथ, तेज नकारात्मक उतार-चढ़ाव के साथ।

एक शब्द में, सहज ज्ञान युक्त अवलोकन से, हम देख सकते हैं कि एक बड़े उतार-चढ़ाव के बाद एक घने उतार-चढ़ाव के साथ एक बड़ी संभावना होगी, जो कि अस्थिरता का एकत्रीकरण प्रभाव भी है। यदि यह अस्थिरता सीमा अनुमानित है, तो यह BTC के अल्पकालिक लेनदेन के लिए मूल्यवान है, जो अस्थिरता पर चर्चा करने का उद्देश्य भी है।

१-३. डेटा तैयार करना

प्रशिक्षण नमूना सेट तैयार करने के लिए, सबसे पहले, हम एक बेंचमार्क नमूना स्थापित करते हैं, जिसमें लघुगणकीय रिटर्न दर समकक्ष अवलोकन की गई अस्थिरता है। क्योंकि दिन की अस्थिरता को सीधे अवलोकन नहीं किया जा सकता है, प्रति घंटे के डेटा का उपयोग दिन की वास्तविक अस्थिरता का अनुमान लगाने के लिए पुनः नमूनाकरण के लिए किया जाता है और इसे अस्थिरता के आश्रित चर के रूप में लिया जाता है।

पुनः नमूनाकरण विधि प्रति घंटे के आंकड़ों पर आधारित है। सूत्र निम्नानुसार दिखाया गया हैः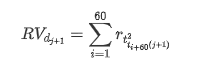

[4] मेंः

count_num = 100000
start_date = '2020-03-01'

df = get_bars('huobi.btc_usdt', '1m', count=50000, start='2020-02-13')  # Take the minute data
kline_1m = pd.DataFrame(df['close'], dtype=np.float)
kline_1m.index.name = 'date'
kline_1m['log_price'] = np.log(kline_1m['close'])
kline_1m['return'] = kline_1m['close'].pct_change().dropna()
kline_1m['log_return'] = kline_1m['log_price'] - kline_1m['log_price'].shift(1)

kline_1m['squared_log_return'] = np.power(kline_1m['log_return'], 2)

kline_1m['return_100x'] = np.multiply(kline_1m['return'], 100)
kline_1m['log_return_100x'] = np.multiply(kline_1m['log_return'], 100)  # Enlarge 100 times

df = get_bars('huobi.btc_usdt', '1h', count=860, start='2020-02-13')  # Take the hour data
kline_all = pd.DataFrame(df['close'], dtype=np.float)
kline_all.index.name = 'date'
kline_all['log_price'] = np.log(kline_all['close'])  # Calculate daily logarithmic rate of return
kline_all['return'] = kline_all['log_price'].pct_change().dropna()
kline_all['log_return'] = kline_all['log_price'] - kline_all['log_price'].shift(1)  # Calculate logarithmic rate of return
kline_all['squared_log_return'] = np.power(kline_all['log_return'], 2)  # The exponential square of logarithmic daily rate of return

kline_all['return_100x'] = np.multiply(kline_all['return'], 100)
kline_all['log_return_100x'] = np.multiply(kline_all['log_return'], 100)  # Enlarge 100 times

kline_all['realized_variance_1_hour'] = kline_1m.loc[:, 'squared_log_return'].resample('h', closed='left', label='left').sum().copy()  # Resampling to days
kline_all['realized_volatility_1_hour'] = np.sqrt(kline_all['realized_variance_1_hour'])  # Volatility of variance derivation

kline_all = kline_all[4:-29] # Remove the last line because it is missing
kline_all.head(3)

बाहर[4]: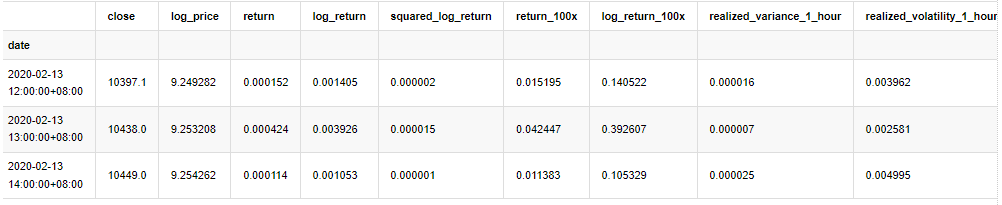

नमूने के बाहर के डेटा को उसी तरह तैयार करें

[5] मेंः

# Prepare the data outside the sample with realized daily volatility
df = get_bars('huobi.btc_usdt', '1m', count=50000, start='2020-02-13')  # Take the minute data
kline_1m = pd.DataFrame(df['close'], dtype=np.float)
kline_1m.index.name = 'date'
kline_1m['log_price'] = np.log(kline_1m['close'])
kline_1m['log_return'] = kline_1m['log_price'] - kline_1m['log_price'].shift(1)
kline_1m['log_return_100x'] = np.multiply(kline_1m['log_return'], 100)  # Enlarge 100 times
kline_1m['squared_log_return'] = np.power(kline_1m['log_return_100x'], 2)
kline_1m#.tail()
df = get_bars('huobi.btc_usdt', '1h', count=860, start='2020-02-13')  # Take the hour data
kline_test = pd.DataFrame(df['close'], dtype=np.float)
kline_test.index.name = 'date'
kline_test['log_price'] = np.log(kline_test['close'])  # Calculate daily logarithmic rate of return
kline_test['log_return'] = kline_test['log_price'] - kline_test['log_price'].shift(1)  # Calculate logarithmic rate of return
kline_test['log_return_100x'] = np.multiply(kline_test['log_return'], 100)  # Enlarge 100 times
kline_test['squared_log_return'] = np.power(kline_test['log_return_100x'], 2)  # The exponential square of logarithmic daily rate of return
kline_test['realized_variance_1_hour'] = kline_1m.loc[:, 'squared_log_return'].resample('h', closed='left', label='left').sum()  # Resampling to days
kline_test['realized_volatility_1_hour'] = np.sqrt(kline_test['realized_variance_1_hour'])  # Volatility of variance derivation
kline_test = kline_test[4:-2]

नमूना के आधारभूत आंकड़ों को समझने के लिए, एक सरल वर्णनात्मक विश्लेषण निम्नानुसार किया जाता हैः

[9] मेंः

line_test = pd.DataFrame(kline_train['log_return'].dropna(), dtype=np.float)
line_test.index.name = 'date'

mean = line_test.mean()  # Calculate mean value and standard deviation
std = line_test.std()

line_test.sort_values(by = 'log_return', inplace = True)  # Resort
s_r = line_test.reset_index(drop = False)  # After resorting, update index
s_r['p'] = (s_r.index - 0.5) / len(s_r)  # Calculate the percentile p(i)
s_r['q'] = (s_r['log_return'] - mean) / std  # Calculate the value of q

st = line_test.describe()
x1 ,y1 = 0.25, st['log_return']['25%']
x2 ,y2 = 0.75, st['log_return']['75%']

fig = plt.figure(figsize = (18,8))
layout = (2, 2)
ax1 = plt.subplot2grid(layout, (0, 0), colspan=2)# Plot the data distribution
ax2 = plt.subplot2grid(layout, (1, 0))# Plot histogram
ax3 = plt.subplot2grid(layout, (1, 1))# Draw the QQ chart, the straight line is the connection of the quarter digit, three-quarters digit, which is basically conforms to the normal distribution

ax1.scatter(line_test.index, line_test.values)
line_test.hist(bins=30,alpha = 0.5,ax = ax2)
line_test.plot(kind = 'kde', secondary_y=True,ax = ax2)
ax3.plot(s_r['p'],s_r['log_return'],'k.',alpha = 0.1)
ax3.plot([x1,x2],[y1,y2],'-r')
sns.despine()
plt.tight_layout()

बाहर[9]:

नतीजतन, लॉगरिथम रिटर्न के समय श्रृंखला चार्ट में अस्थिरता संचलन और लाभप्रदता प्रभाव स्पष्ट है।

लघुगणकीय प्रतिफलों के वितरण चार्ट में विकृति 0 से कम है, यह दर्शाता है कि नमूना में प्रतिफल थोड़ा नकारात्मक और दाईं ओर पक्षपाती हैं। लघुगणकीय प्रतिफलों के QQ चार्ट में, हम देख सकते हैं कि लघुगणकीय प्रतिफलों का वितरण सामान्य नहीं है।

डेटा वितरण की विकृति 1 से कम है, यह दर्शाता है कि नमूना के भीतर रिटर्न थोड़ा सकारात्मक और थोड़ा सही पक्षपाती हैं। कर्टोसिस मान 3 से अधिक है, यह दर्शाता है कि उपज मोटी वसा पूंछ वितरित है।

अब जब हम इस बिंदु पर पहुंच गए हैं, तो एक और सांख्यिकीय परीक्षण करें। [7] मेंः

line_test = pd.DataFrame(kline_all['log_return'].dropna(), dtype=np.float)
line_test.index.name = 'date'
mean = line_test.mean()
std = line_test.std()
normal_result = pd.DataFrame(index=['Mean Value', 'Std Value', 'Skewness Value','Kurtosis Value',
                                    'Ks Test Value','Ks Test P-value',
                                    'Jarque Bera Test','Jarque Bera Test P-value'],
                    columns=['model value'])
normal_result['model value']['Mean Value'] = ('%.4f'% mean[0])
normal_result['model value']['Std Value'] = ('%.4f'% std[0])
normal_result['model value']['Skewness Value'] = ('%.4f'% line_test.skew())
normal_result['model value']['Kurtosis Value'] = ('%.4f'% line_test.kurt())
normal_result['model value']['Ks Test Value'] = stats.kstest(line_test, 'norm', (mean, std))[0]
normal_result['model value']['Ks Test P-value'] = stats.kstest(line_test, 'norm', (mean, std))[1]
normal_result['model value']['Jarque Bera Test'] = stats.jarque_bera(line_test)[0]
normal_result['model value']['Jarque Bera Test P-value'] = stats.jarque_bera(line_test)[1]
normal_result

बाहर[7]:

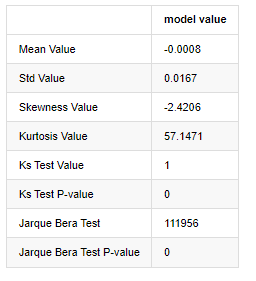
कोल्मोगोरोव-स्मिर्नोव और जार्के-बेरा परीक्षण सांख्यिकी का प्रयोग क्रमशः किया जाता है। मूल परिकल्पना महत्वपूर्ण अंतर और सामान्य वितरण की विशेषता है। यदि पी मान 0.05% आत्मविश्वास स्तर के महत्वपूर्ण मूल्य से कम है, तो मूल परिकल्पना को अस्वीकार कर दिया जाता है।

यह देखा जा सकता है कि कर्टोसिस मान 3 से अधिक है, जो मोटी वसा पूंछ की विशेषताओं को दर्शाता है। केएस और जेबी के पी मान आत्मविश्वास अंतराल से कम हैं। सामान्य वितरण की धारणा को खारिज कर दिया गया है, जो साबित करता है कि बीटीसी की रिटर्न दर में सामान्य वितरण की विशेषताओं नहीं हैं, और अनुभवजन्य अध्ययन में मोटी वसा पूंछ की विशेषताओं हैं।

1-4. वास्तविक अस्थिरता और अवलोकन अस्थिरता की तुलना

हम observation के लिए square_log_ return (logarithmic yield squared) और realized_variance (realized variance) को जोड़ते हैं।

[11] मेंः

fig, ax = plt.subplots(figsize=(18, 6))
start = '2020-03-08 00:00:00+08:00'
end = '2020-03-20 00:00:00+08:00'

np.abs(kline_all['squared_log_return']).loc[start:end].plot(ax=ax,label='squared log return')
kline_all['realized_variance_1_hour'].loc[start:end].plot(ax=ax,label='realized variance')
plt.legend(loc='best')

बाहर[11]:

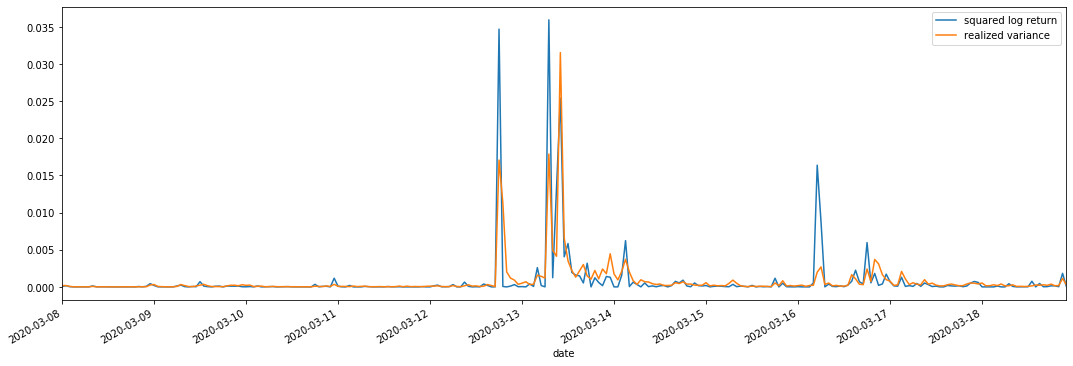
यह देखा जा सकता है कि जब वास्तविक भिन्नता सीमा अधिक होती है, तो रिटर्न दर सीमा की अस्थिरता भी अधिक होती है, और वास्तविक रिटर्न दर अधिक चिकनी होती है। दोनों स्पष्ट संचयन प्रभावों का निरीक्षण करना आसान हैं।

विशुद्ध रूप से सैद्धांतिक दृष्टिकोण से, आरवी वास्तविक अस्थिरता के करीब है, जबकि अल्पकालिक अस्थिरता को समतल किया जाता है क्योंकि इंट्राडे अस्थिरता ओवरनाइट डेटा से संबंधित है, इसलिए अवलोकन के दृष्टिकोण से, इंट्राडे अस्थिरता अस्थिरता शेयर बाजार की कम आवृत्ति के लिए अधिक उपयुक्त है। उच्च आवृत्ति व्यापार और बीटीसी की 7 * 24 घंटे बाजार विशेषताएं आरवी को बेंचमार्क अस्थिरता निर्धारित करने के लिए अधिक उपयुक्त बनाती हैं।

2. समय श्रृंखलाओं की सुचारूता

यदि यह एक गैर-स्थिर श्रृंखला है, तो इसे लगभग एक स्थिर श्रृंखला में समायोजित करने की आवश्यकता है। सामान्य तरीका अंतर प्रसंस्करण करना है। सैद्धांतिक रूप से, कई बार अंतर के बाद, गैर-स्थिर श्रृंखला को एक स्थिर श्रृंखला के करीब किया जा सकता है। यदि नमूना श्रृंखला का सह-विभिन्नता स्थिर है, तो इसकी टिप्पणियों की अपेक्षा, भिन्नता और सह-विभिन्नता समय के साथ नहीं बदलेगी, यह दर्शाता है कि नमूना श्रृंखला सांख्यिकीय विश्लेषण में निष्कर्ष के लिए अधिक सुविधाजनक है।

इकाई रूट परीक्षण, अर्थात् एडीएफ परीक्षण, का उपयोग यहां किया जाता है। एडीएफ परीक्षण महत्व का निरीक्षण करने के लिए टी परीक्षण का उपयोग करता है। सिद्धांत रूप में, यदि श्रृंखला स्पष्ट प्रवृत्ति नहीं दिखाती है, तो केवल निरंतर आइटम बनाए रखे जाते हैं। यदि श्रृंखला में प्रवृत्ति है, तो प्रतिगमन समीकरण में निरंतर आइटम और समय प्रवृत्ति आइटम दोनों शामिल होने चाहिए। इसके अलावा, सूचना मानदंडों के आधार पर मूल्यांकन के लिए एआईसी और बीआईसी मानदंडों का उपयोग किया जा सकता है। यदि सूत्र की आवश्यकता होती है, तो यह निम्नानुसार हैः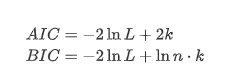

[8] मेंः

stable_test = kline_all['log_return']
adftest = sm.tsa.stattools.adfuller(np.array(stable_test), autolag='AIC')
adftest2 = sm.tsa.stattools.adfuller(np.array(stable_test), autolag='BIC')
output=pd.DataFrame(index=['ADF Statistic Test Value', "ADF P-value", "Lags", "Number of Observations",
                           "Critical Value(1%)","Critical Value(5%)","Critical Value(10%)"],
                    columns=['AIC','BIC'])
output['AIC']['ADF Statistic Test Value'] = adftest[0]
output['AIC']['ADF P-value'] = adftest[1]
output['AIC']['Lags'] = adftest[2]
output['AIC']['Number of Observations'] = adftest[3]
output['AIC']['Critical Value(1%)'] = adftest[4]['1%']
output['AIC']['Critical Value(5%)'] = adftest[4]['5%']
output['AIC']['Critical Value(10%)'] = adftest[4]['10%']
output['BIC']['ADF Statistic Test Value'] = adftest2[0]
output['BIC']['ADF P-value'] = adftest2[1]
output['BIC']['Lags'] = adftest2[2]
output['BIC']['Number of Observations'] = adftest2[3]
output['BIC']['Critical Value(1%)'] = adftest2[4]['1%']
output['BIC']['Critical Value(5%)'] = adftest2[4]['5%']
output['BIC']['Critical Value(10%)'] = adftest2[4]['10%']
output

बाहर[8]: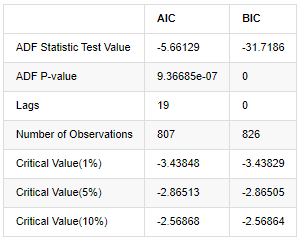

मूल धारणा यह है कि श्रृंखला में कोई यूनिट रूट नहीं है, यानी वैकल्पिक धारणा यह है कि श्रृंखला स्थिर है। परीक्षण पी मूल्य 0.05% आत्मविश्वास स्तर कट-ऑफ मूल्य से बहुत कम है, मूल धारणा को अस्वीकार करें, इसलिए लॉग दर की वापसी एक स्थिर श्रृंखला है, सांख्यिकीय समय श्रृंखला मॉडल का उपयोग करके मॉडलिंग की जा सकती है।

3. मॉडल की पहचान और आदेश निर्धारण

औसत मान समीकरण को स्थापित करने के लिए, यह सुनिश्चित करने के लिए अनुक्रम पर एक ऑटोकोरेलेशन परीक्षण करना आवश्यक है कि त्रुटि शब्द में ऑटोकोरेलेशन नहीं है। सबसे पहले, ऑटोकोरेलेशन एसीएफ और आंशिक सहसंबंध पीएसीएफ को निम्नानुसार प्लॉट करने का प्रयास करेंः

[19] मेंः

tsplot(kline_all['log_return'], kline_all['log_return'], title='Log Return', lags=100)

बाहर[19]:

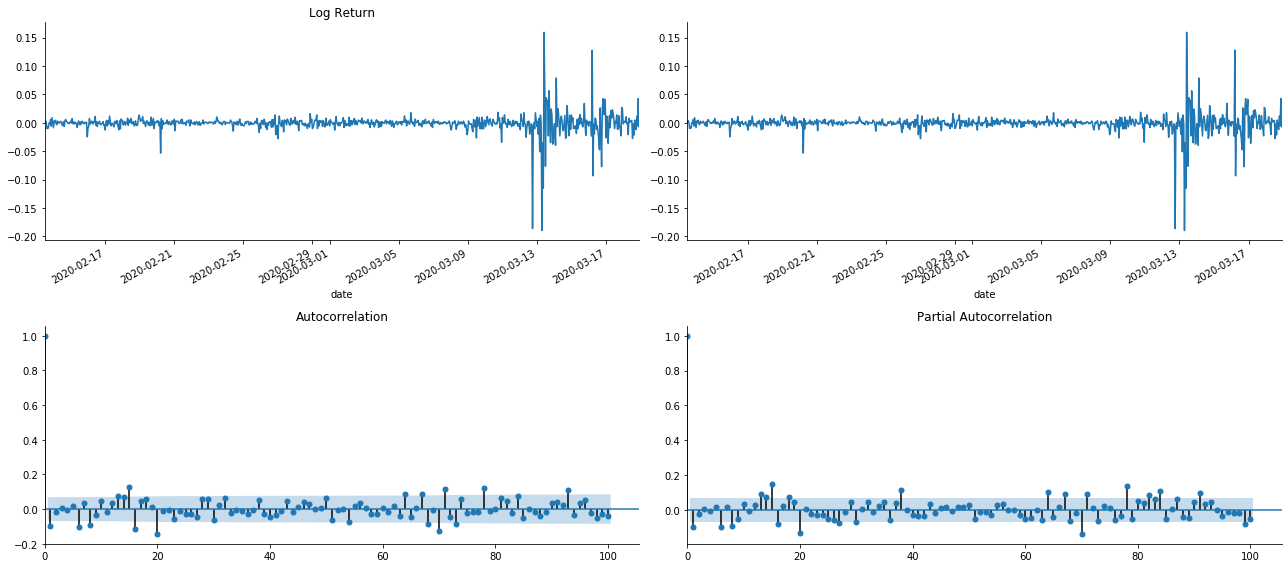
यह देखा जा सकता है कि टर्नकेशन का प्रभाव एकदम सही है। उस समय, इस चित्र ने मुझे एक प्रेरणा दी। क्या बाजार वास्तव में अमान्य है? सत्यापित करने के लिए, हम वापसी श्रृंखला पर ऑटोकोरेलेशन विश्लेषण करेंगे और मॉडल के लेग ऑर्डर का निर्धारण करेंगे।

आमतौर पर इस्तेमाल किया जाने वाला सहसंबंध गुणांक उसके और अपने बीच सहसंबंध को मापने के लिए होता है, अर्थात अतीत में एक निश्चित समय में r ((t) और r (t-l) के बीच सहसंबंधः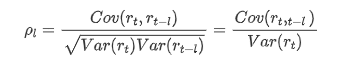

फिर चलो एक मात्रात्मक परीक्षण करते हैं। मूल धारणा यह है कि सभी ऑटोकोरेलेशन गुणांक 0 हैं, अर्थात श्रृंखला में कोई ऑटोकोरेलेशन नहीं है। परीक्षण सांख्यिकी सूत्र निम्नानुसार लिखा गया हैः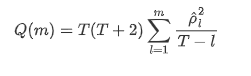

विश्लेषण के लिए निम्नानुसार दस ऑटोकोरेलेशन गुणांक लिए गए:

[9] मेंः

acf,q,p = sm.tsa.acf(kline_all['log_return'], nlags=15,unbiased=True,qstat = True, fft=False)  # Test 10 autocorrelation coefficients
output = pd.DataFrame(np.c_[range(1,16), acf[1:], q, p], columns=['lag', 'ACF', 'Q', 'P-value'])
output = output.set_index('lag')
output

बाहर[9]: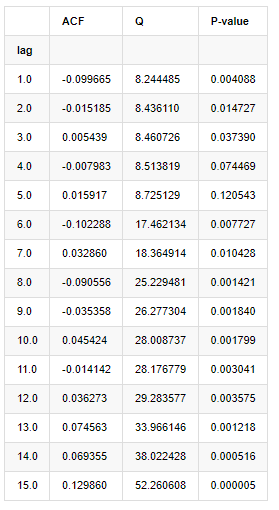

परीक्षण सांख्यिकी Q और पी-मूल्य के अनुसार, हम देख सकते हैं कि ऑटोकोरेलेशन फ़ंक्शन ACF क्रम 0 के बाद धीरे-धीरे 0 हो जाता है। Q परीक्षण सांख्यिकी के पी-मूल्य मूल धारणा को अस्वीकार करने के लिए पर्याप्त छोटे हैं, इसलिए श्रृंखला में ऑटोकोरेलेशन है।

4. एआरएमए मॉडलिंग

एआर और एमए मॉडल काफी सरल हैं। इसे सरलता से रखने के लिए, मार्कडाउन सूत्र लिखने के लिए बहुत थक गया है। यदि आप रुचि रखते हैं, तो कृपया उन्हें स्वयं जांचें। एआर (ऑटोरेग्रेशन) मॉडल का उपयोग मुख्य रूप से समय श्रृंखलाओं को मॉडल करने के लिए किया जाता है। यदि श्रृंखला ने एसीएफ परीक्षण पारित किया है, अर्थात, 1 के अंतराल के साथ ऑटोकोरेलेशन गुणांक महत्वपूर्ण है, अर्थात, समय पर डेटा समय की भविष्यवाणी के लिए उपयोगी हो सकता है।

एमए (मोविंग एवरेज) मॉडल वर्तमान पूर्वानुमान मूल्य को रैखिक रूप से व्यक्त करने के लिए पिछले q अवधियों की यादृच्छिक हस्तक्षेप या त्रुटि भविष्यवाणी का उपयोग करता है।

डेटा की गतिशील संरचना को पूरी तरह से वर्णन करने के लिए, एआर या एमए मॉडल के क्रम को बढ़ाना आवश्यक है, लेकिन ऐसे मापदंड गणना को अधिक जटिल बना देंगे। इसलिए, इस प्रक्रिया को सरल करने के लिए, एक ऑटोरेग्रेसिव चलती औसत (एआरएमए) मॉडल प्रस्तावित है।

चूंकि मूल्य समय श्रृंखलाएं आम तौर पर गैर-स्थिर होती हैं, और स्थिरता पर अंतर पद्धति के अनुकूलन प्रभाव पर पहले चर्चा की गई है, इसलिए एआरआईएमए (पी, डी, क्यू) (सम्मा ऑटोरेग्रेसिव मूविंग एवरेज) मॉडल मौजूदा मॉडल के अनुप्रयोग के आधार पर डी-ऑर्डर अंतर प्रसंस्करण को जोड़ता है। हालांकि, चूंकि हमने लघुगणक का उपयोग किया है, इसलिए हम सीधे एआरएमए (पी, क्यू) का उपयोग कर सकते हैं।

एक शब्द में, एआरआईएमए मॉडल और एआरएमए मॉडल निर्माण प्रक्रिया के बीच एकमात्र अंतर यह है कि यदि स्थिरता का विश्लेषण करने के बाद अस्थिर परिणाम प्राप्त किए जाते हैं, तो मॉडल सीधे श्रृंखला के लिए एक वर्गिक अंतर करेगा और फिर स्थिरता परीक्षण करेगा, और फिर श्रृंखला स्थिर होने तक क्रम पी और क्यू निर्धारित करेगा। मॉडल के निर्माण और मूल्यांकन के बाद, बाद की भविष्यवाणी की जाएगी, अंतर करने के लिए वापस जाने के चरण को समाप्त कर देगा। हालांकि, कीमत का दूसरे क्रम का अंतर अर्थहीन है, इसलिए एआरएमए सबसे अच्छा विकल्प है।

4-1. आदेश का चयन

इसके बाद, हम सीधे सूचना मानदंड द्वारा क्रम का चयन कर सकते हैं, यहाँ हम इसे एआईसी और बीआईसी के थर्मोडायनामिक आरेखों के साथ कोशिश करते हैं।

[10] मेंः

def select_best_params():
    ps = range(0, 4)
    ds= range(1, 2)
    qs = range(0, 4)
    parameters = product(ps, ds, qs)
    parameters_list = list(parameters)

    p_min = 0
    d_min = 0
    q_min = 0
    p_max = 3
    d_max = 3
    q_max = 3

    results_aic = pd.DataFrame(index=['AR{}'.format(i) for i in range(p_min,p_max+1)],
                               columns=['MA{}'.format(i) for i in range(q_min,q_max+1)])
    results_bic = pd.DataFrame(index=['AR{}'.format(i) for i in range(p_min,p_max+1)],
                               columns=['MA{}'.format(i) for i in range(q_min,q_max+1)])
    
    best_params = []
    aic_results = []
    bic_results = []
    hqic_results = []
    best_aic = float("inf")
    best_bic = float("inf")
    best_hqic = float("inf")
    warnings.filterwarnings('ignore')
    for param in parameters_list:
        try:
            model = sm.tsa.SARIMAX(kline_all['log_price'], order=(param[0], param[1], param[2])).fit(disp=-1)
            results_aic.loc['AR{}'.format(param[0]), 'MA{}'.format(param[2])] = model.aic
            results_bic.loc['AR{}'.format(param[0]), 'MA{}'.format(param[2])] = model.bic
        except ValueError:
            continue    
           
        aic_results.append([param, model.aic])
        bic_results.append([param, model.bic])
        hqic_results.append([param, model.hqic])
    
    results_aic = results_aic[results_aic.columns].astype(float)
    results_bic = results_bic[results_bic.columns].astype(float)
    
    # Draw thermodynamic diagrams of AIC and BIC to find the best
    fig = plt.figure(figsize=(18, 9))
    layout = (2, 2)
    aic_ax = plt.subplot2grid(layout, (0, 0))
    bic_ax = plt.subplot2grid(layout, (0, 1))

    aic_ax = sns.heatmap(results_aic,mask=results_aic.isnull(),ax=aic_ax,cmap='OrRd',annot=True,fmt='.2f',);
    aic_ax.set_title('AIC');
    bic_ax = sns.heatmap(results_bic,mask=results_bic.isnull(),ax=bic_ax,cmap='OrRd',annot=True,fmt='.2f',);
    bic_ax.set_title('BIC');
    
    aic_df = pd.DataFrame(aic_results)
    aic_df.columns = ['params', 'aic']   
    best_params.append(aic_df.params[aic_df.aic.idxmin()])
    print('AIC best param: {}'.format(aic_df.params[aic_df.aic.idxmin()]))
    
    bic_df = pd.DataFrame(bic_results)
    bic_df.columns = ['params', 'bic']
    best_params.append(bic_df.params[bic_df.bic.idxmin()])
    print('BIC best param: {}'.format(bic_df.params[bic_df.bic.idxmin()]))
    
    hqic_df = pd.DataFrame(hqic_results)
    hqic_df.columns = ['params', 'hqic']
    best_params.append(hqic_df.params[hqic_df.hqic.idxmin()])
    print('HQIC best param: {}'.format(hqic_df.params[hqic_df.hqic.idxmin()]))

    for best_param in best_params:
        if best_params.count(best_param)>=2:
            print('Best Param Selected: {}'.format(best_param))
            return best_param 

best_param = select_best_params()

बाहर[10]: एआईसी सर्वोत्तम पैरामीटरः (0, 1, 1) बीआईसी सर्वश्रेष्ठ पैरामीटरः (0, 1, 1) HQIC का सर्वश्रेष्ठ पैरामीटरः (0, 1, 1) सर्वश्रेष्ठ पैराम चयनितः (0, 1, 1)

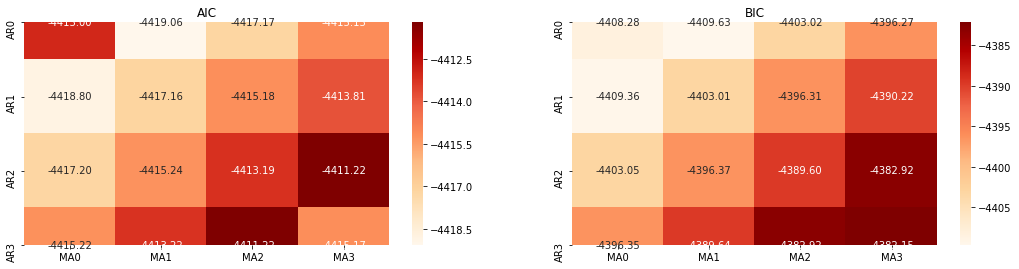
यह स्पष्ट है कि लॉगरिदमिक मूल्य के लिए इष्टतम प्रथम-क्रम पैरामीटर संयोजन (0,1,1) है, जो सरल और सीधा है। लॉग_रिटर्न (लॉगरिदमिक रिटर्न की दर) एक ही ऑपरेशन करता है। एआईसी इष्टतम मूल्य (4,3) है, और बीआईसी इष्टतम मूल्य (0,1) है। इसलिए लॉग_रिटर्न (लॉगरिदमिक रिटर्न की दर) के लिए पैरामीटर का इष्टतम संयोजन (0,1) है।

4-2। एआरएमए मॉडलिंग और मिलान

त्रैमासिक गुणांक की आवश्यकता नहीं है, लेकिन SARIMAX गुणों में अधिक समृद्ध है, इसलिए मॉडलिंग के लिए इस मॉडल को चुनने का निर्णय लिया गया और संयोग से निम्नानुसार एक वर्णनात्मक विश्लेषण तैयार किया गयाः

[11] मेंः

params = (0, 0, 1)
training_model = smt.SARIMAX(endog=kline_all['log_return'], trend='c', order=params, seasonal_order=(0, 0, 0, 0))
model_results = training_model.fit(disp=False)
model_results.summary()

बाहर[11]: स्टेटस्पेस मॉडल परिणाम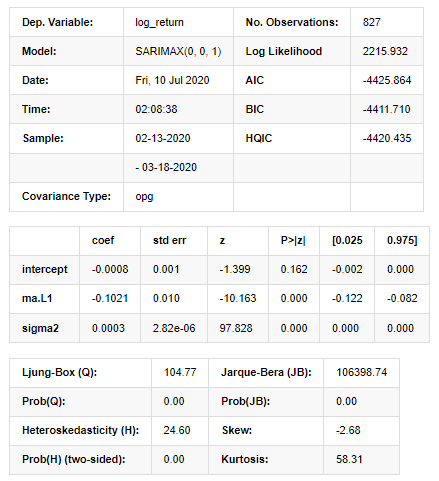

चेतावनीः [1] ग्रेडिएंट्स के बाहरी उत्पाद (जटिल-चरण) का उपयोग करके गणना की जाने वाली सह-विभेदकता मैट्रिक्स। [27] मेंः

model_results.plot_diagnostics(figsize=(18, 10));

बाहर[27]:

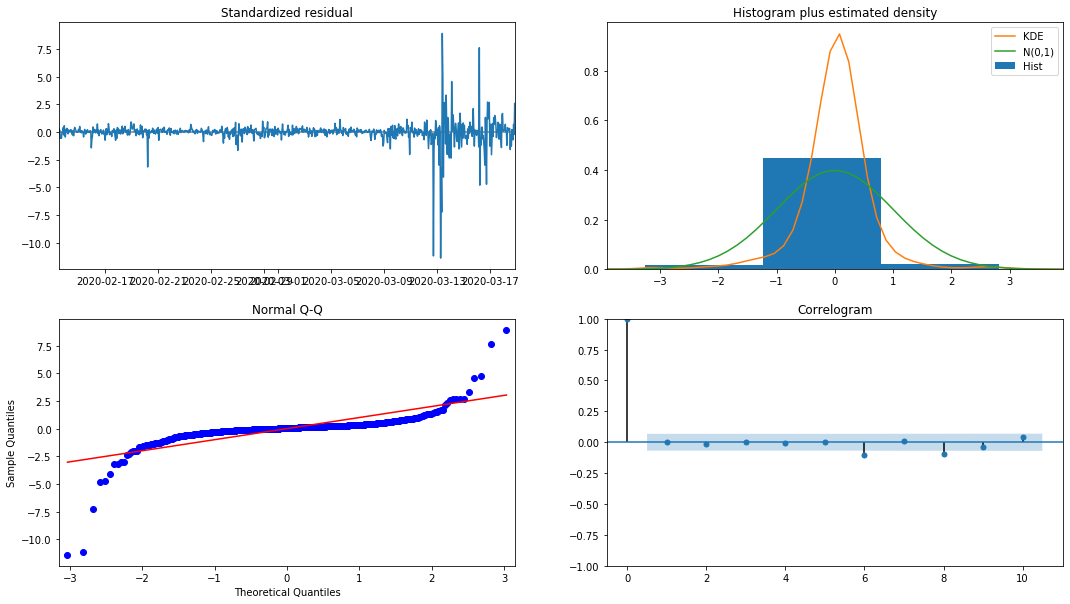
हिस्टोग्राम में संभावना घनत्व KDE सामान्य वितरण N (0,1) से दूर है, यह दर्शाता है कि अवशिष्ट एक सामान्य वितरण नहीं है। QQ क्वांटिल ग्राफ में, मानक सामान्य वितरण से नमूने लिए गए नमूनों के अवशेष पूरी तरह से रैखिक प्रवृत्ति का पालन नहीं करते हैं, इसलिए यह फिर से पुष्टि की जाती है कि अवशेष सामान्य वितरण नहीं हैं और सफेद शोर के करीब हैं।

फिर, यह कहते हुए, क्या मॉडल का उपयोग किया जा सकता है अभी भी परीक्षण किया जाना चाहिए।

4-3. मॉडल परीक्षण

अवशिष्ट का मिलान प्रभाव आदर्श नहीं है, इसलिए हमने उस पर डर्बिन वाटसन परीक्षण किया। परीक्षण की मूल परिकल्पना यह है कि अनुक्रम में ऑटोकोरेलेशन नहीं है, और वैकल्पिक परिकल्पना अनुक्रम स्थिर है। इसके अलावा, यदि एलबी, जेबी और एच परीक्षणों के पी मान 0.05% आत्मविश्वास स्तर के महत्वपूर्ण मूल्य से कम हैं, तो मूल परिकल्पना को खारिज कर दिया जाएगा।

[12] मेंः

het_method='breakvar'
norm_method='jarquebera'
sercor_method='ljungbox'

(het_stat, het_p) = model_results.test_heteroskedasticity(het_method)[0]
norm_stat, norm_p, skew, kurtosis = model_results.test_normality(norm_method)[0]

sercor_stat, sercor_p = model_results.test_serial_correlation(method=sercor_method)[0]
sercor_stat = sercor_stat[-1] # The last value of the maximum period
sercor_p = sercor_p[-1]

dw = sm.stats.stattools.durbin_watson(model_results.filter_results.standardized_forecasts_error[0, model_results.loglikelihood_burn:])

arroots_outside_unit_circle = np.all(np.abs(model_results.arroots) > 1)
maroots_outside_unit_circle = np.all(np.abs(model_results.maroots) > 1)

print('Test heteroskedasticity of residuals ({}): stat={:.3f}, p={:.3f}'.format(het_method, het_stat, het_p));
print('\nTest normality of residuals ({}): stat={:.3f}, p={:.3f}'.format(norm_method, norm_stat, norm_p));
print('\nTest serial correlation of residuals ({}): stat={:.3f}, p={:.3f}'.format(sercor_method, sercor_stat, sercor_p));
print('\nDurbin-Watson test on residuals: d={:.2f}\n\t(NB: 2 means no serial correlation, 0=pos, 4=neg)'.format(dw))
print('\nTest for all AR roots outside unit circle (>1): {}'.format(arroots_outside_unit_circle))
print('\nTest for all MA roots outside unit circle (>1): {}'.format(maroots_outside_unit_circle))

root_test=pd.DataFrame(index=['Durbin-Watson test on residuals','Test for all AR roots outside unit circle (>1)','Test for all MA roots outside unit circle (>1)'],columns=['c'])
root_test['c']['Durbin-Watson test on residuals']=dw
root_test['c']['Test for all AR roots outside unit circle (>1)']=arroots_outside_unit_circle
root_test['c']['Test for all MA roots outside unit circle (>1)']=maroots_outside_unit_circle
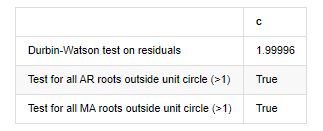
root_test

बाहर[12]: अवशेषों की परीक्षण हेटरोस्केडेस्टिकता (ब्रेकवार): स्टैट=24.598, पी=0.000

अवशेषों (जार्क्वेबेरा) की परीक्षण सामान्यताः stat=106398.739, p=0.000

अवशेषों का परीक्षण सीरियल सहसंबंध (ljungbox): stat=104.767, p=0.000

अवशेषों पर डर्बिन-वॉटसन परीक्षण: d=2.00 (नोट: 2 का अर्थ है कोई सीरियल सहसंबंध नहीं, 0=पोस, 4=नकारात्मक)

यूनिट सर्कल के बाहर सभी AR जड़ों के लिए परीक्षण (>1): सच

इकाई वृत्त के बाहर सभी एमए जड़ों के लिए परीक्षण (>1): सही

[13] मेंः

kline_all['log_price_dif1'] = kline_all['log_price'].diff(1)
kline_all = kline_all[1:]
kline_train = kline_all

training_label = 'log_return'
training_ts = pd.DataFrame(kline_train[training_label], dtype=np.float)

delta = model_results.fittedvalues - training_ts[training_label]
adjR = 1 - delta.var()/training_ts[training_label].var()
adjR_test=pd.DataFrame(index=['adjR2'],columns=['Value'])
adjR_test['Value']['adjR2']=adjR**2
adjR_test

बाहर[13]:

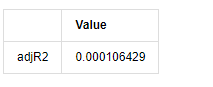
यदि डर्बिन वाटसन परीक्षण सांख्यिकी 2 के बराबर है, तो पुष्टि करता है कि श्रृंखला में कोई सहसंबंध नहीं है, और इसका सांख्यिकीय मूल्य (0,4) के बीच वितरित किया गया है। 0 के करीब होने का मतलब है कि सकारात्मक सहसंबंध उच्च है, जबकि 4 के करीब होने का मतलब है कि नकारात्मक सहसंबंध उच्च है। यहां यह लगभग 2 के बराबर है। अन्य परीक्षणों का पी मूल्य पर्याप्त छोटा है, इकाई विशेषता जड़ इकाई वृत्त के बाहर है, और संशोधित एडजआर 2 का मूल्य जितना बड़ा होगा, उतना बेहतर होगा। माप का समग्र परिणाम संतोषजनक नहीं लगता है।

[14] मेंः

model_results.params

बाहर[1]: अवरोधन -0.000817 ma.L1 -0.102102 सिग्मा2 0.000275 dtype: float64

संक्षेप में, यह आदेश सेटिंग पैरामीटर मूल रूप से समय श्रृंखला मॉडलिंग और बाद में अस्थिरता मॉडलिंग की आवश्यकताओं को पूरा कर सकता है, लेकिन मिलान प्रभाव ऐसा-वैसा है। मॉडल अभिव्यक्ति निम्नानुसार हैः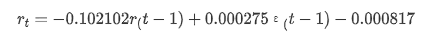

4-4. मॉडल भविष्यवाणी

इसके बाद, प्रशिक्षित मॉडल को आगे मिलान किया जाता है। statsmodels मिलान और पूर्वानुमान के लिए स्थिर और गतिशील विकल्प प्रदान करता है। अंतर यह है कि क्या पूर्वानुमान के अगले चरण में अवलोकन मूल्य का उपयोग किया जाता है, या पिछले चरण में उत्पन्न भविष्यवाणी मूल्य का उपयोग पुनरावृत्ति से किया जाता है। लॉग_रिटर्न (रिटर्न की लघुगणकीय दर) के भविष्यवाणी प्रभाव इस प्रकार हैंः

[37] मेंः

start_date = '2020-02-28 12:00:00+08:00'
end_date = start_date 

pred_dy = model_results.get_prediction(start=start_date, dynamic=False)
pred_dy_ci = pred_dy.conf_int()

fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(18, 6))
ax.plot(kline_all['log_return'].loc[start_date:], label='Log Return', linestyle='-')
ax.plot(pred_dy.predicted_mean.loc[start_date:], label='Forecast Log Return', linestyle='--')
ax.fill_between(pred_dy_ci.index,pred_dy_ci.iloc[:, 0],pred_dy_ci.iloc[:, 1], color='g', alpha=.25)

plt.ylabel("BTC Log Return")
plt.legend(loc='best')
plt.tight_layout()
sns.despine()

बाहर[37]:

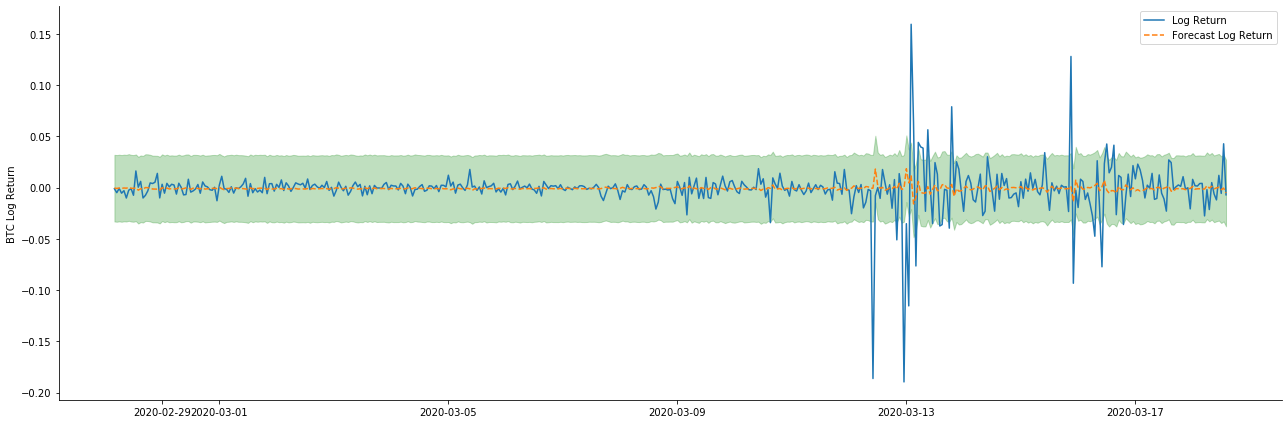
यह देखा जा सकता है कि नमूना पर स्थैतिक मोड का फिट प्रभाव उत्कृष्ट है, नमूना डेटा लगभग 95% आत्मविश्वास अंतराल तक कवर किया जा सकता है, और गतिशील मोड थोड़ा नियंत्रण से बाहर है।

तो चलो गतिशील मोड में डेटा मिलान प्रभाव पर एक नज़र डालते हैंः

[38] मेंः

start_date = '2020-02-28 12:00:00+08:00'
end_date = start_date 

pred_dy = model_results.get_prediction(start=start_date, dynamic=True)
pred_dy_ci = pred_dy.conf_int()

fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(18, 6))
ax.plot(kline_all['log_return'].loc[start_date:], label='Log Return', linestyle='-')
ax.plot(pred_dy.predicted_mean.loc[start_date:], label='Forecast Log Return', linestyle='--')
ax.fill_between(pred_dy_ci.index,pred_dy_ci.iloc[:, 0],pred_dy_ci.iloc[:, 1], color='g', alpha=.25)

plt.ylabel("BTC Log Return")
plt.legend(loc='best')
plt.tight_layout()
sns.despine()

बाहर[38]:

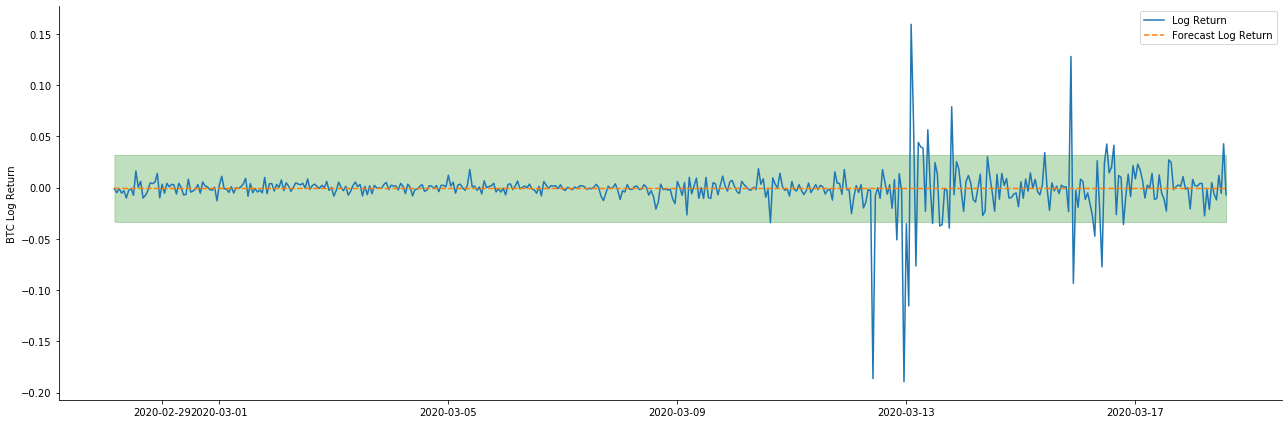
यह देखा जा सकता है कि नमूने पर दोनों मॉडलों का फिट प्रभाव उत्कृष्ट है, और औसत मूल्य लगभग 95% आत्मविश्वास अंतराल द्वारा कवर किया जा सकता है, लेकिन स्थिर मॉडल स्पष्ट रूप से अधिक उपयुक्त है। इसके बाद, आइए 50 चरणों के पूर्वानुमान प्रभाव को देखें।

[41] मेंः

# Out-of-sample predicted data predict()
start_date = '2020-03-01 12:00:00+08:00'
end_date = '2020-03-20 23:00:00+08:00'
model = False

predict_step = 50
predicts_ARIMA_normal = model_results.get_prediction(start=start_date, dynamic=model, full_reports=True)
ci_normal = predicts_ARIMA_normal.conf_int().loc[start_date:]

predicts_ARIMA_normal_out = model_results.get_forecast(steps=predict_step, dynamic=model)
ci_normal_out = predicts_ARIMA_normal_out.conf_int().loc[start_date:end_date]

fig, ax = plt.subplots(figsize=(18,8))
kline_test.loc[start_date:end_date, 'log_return'].plot(ax=ax, label='Benchmark Log Return')

predicts_ARIMA_normal.predicted_mean.plot(ax=ax, style='g', label='In Sample Forecast')
ax.fill_between(ci_normal.index, ci_normal.iloc[:,0], ci_normal.iloc[:,1], color='g', alpha=0.1)

predicts_ARIMA_normal_out.predicted_mean.loc[:end_date].plot(ax=ax, style='r--', label='Out of Sample Forecast')
ax.fill_between(ci_normal_out.index, ci_normal_out.iloc[:,0], ci_normal_out.iloc[:,1], color='r', alpha=0.1)

plt.tight_layout()
plt.legend(loc='best')
sns.despine()

बाहर[41]:

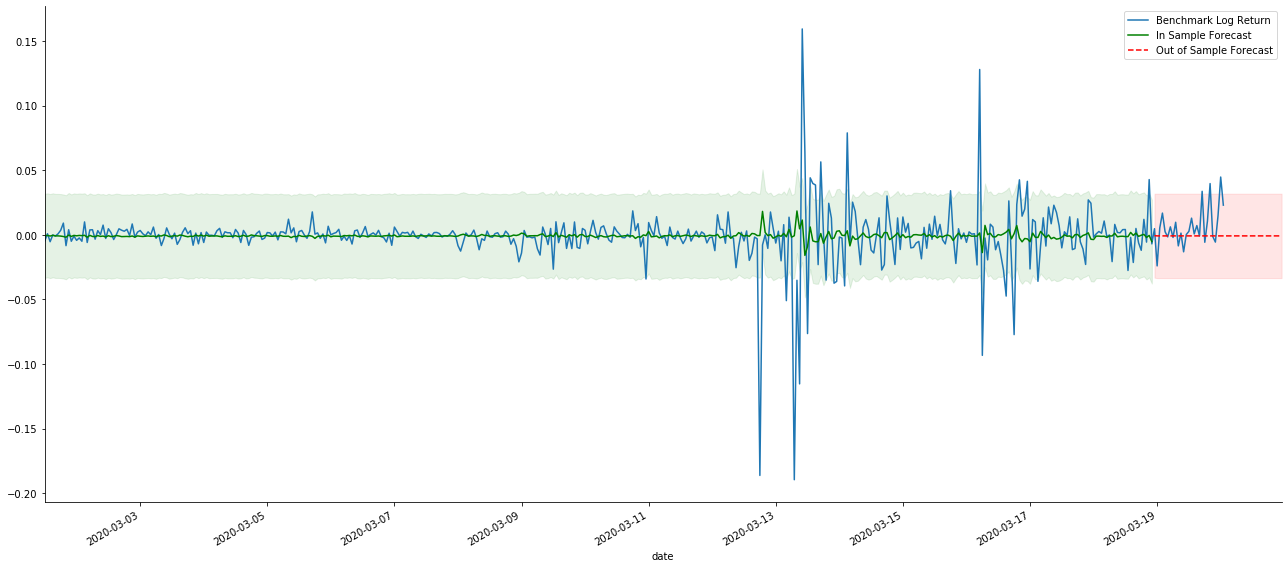
चूंकि नमूना में डेटा का मिलान एक रोलिंग फॉरवर्ड भविष्यवाणी है, जब नमूना में जानकारी की मात्रा पर्याप्त होती है, तो स्थैतिक मॉडल ओवर-मैचिंग के लिए प्रवण होता है, जबकि गतिशील मॉडल में विश्वसनीय आश्रित चर की कमी होती है, और प्रभाव पुनरावृत्ति के बाद बदतर और बदतर हो जाता है। जब नमूना के बाहर डेटा का पूर्वानुमान लगाते हैं, तो मॉडल नमूना के भीतर गतिशील मॉडल के बराबर होता है, इसलिए दीर्घकालिक भविष्यवाणी की त्रुटि अवधि की सटीकता कम होने के लिए बाध्य है।

यदि हम प्रतिफल दर पूर्वानुमान को लॉग_प्राइस (लॉगरिथमिक मूल्य) में उलटा करते हैं, तो मैच नीचे दिए गए चित्र में दिखाया गया हैः

[42] मेंः

params = (0, 1, 1)
mod = smt.SARIMAX(endog=kline_all['log_price'], trend='c', order=params, seasonal_order=(0, 0, 0, 0))
res = mod.fit(disp=False)

start_date = '2020-03-01 12:00:00+08:00'
end_date = '2020-03-15 23:00:00+08:00'

predicts_ARIMA_normal = res.get_prediction(start=start_date, dynamic=False, full_results=False)
predicts_ARIMA_dynamic = res.get_prediction(start=start_date, dynamic=True, full_results=False)

fig, ax = plt.subplots(figsize=(18,6))
kline_test.loc[start_date:end_date, 'log_price'].plot(ax=ax, label='Log Price')

predicts_ARIMA_normal.predicted_mean.loc[start_date:end_date].plot(ax=ax, style='r--', label='Normal Prediction')
ci_normal = predicts_ARIMA_normal.conf_int().loc[start_date:end_date]
ax.fill_between(ci_normal.index, ci_normal.iloc[:,0], ci_normal.iloc[:,1], color='r', alpha=0.1)

predicts_ARIMA_dynamic.predicted_mean.loc[start_date:end_date].plot(ax=ax, style='g', label='Dynamic Prediction')
ci_dynamic = predicts_ARIMA_dynamic.conf_int().loc[start_date:end_date]
ax.fill_between(ci_dynamic.index, ci_dynamic.iloc[:,0], ci_dynamic.iloc[:,1], color='g', alpha=0.1)

plt.tight_layout()
plt.legend(loc='best')
sns.despine()

बाहर[42]:

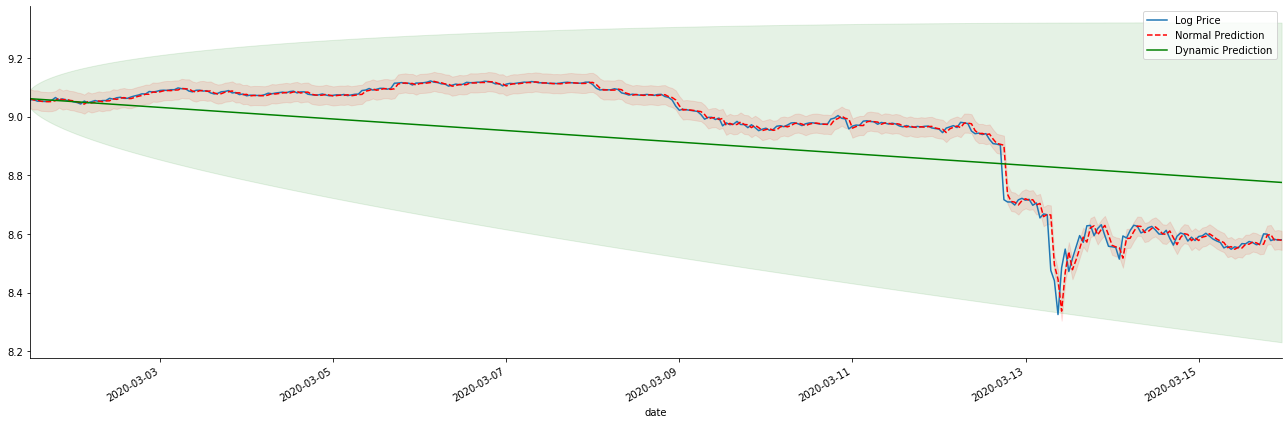
स्थिर मॉडल के मिलान फायदे और दीर्घकालिक भविष्यवाणी में गतिशील मॉडल और स्थिर मॉडल के बीच चरम अंतर को देखना आसान है। लाल धब्बेदार रेखा और गुलाबी सीमा... आप यह नहीं कह सकते कि इस मॉडल की भविष्यवाणी गलत है। आखिरकार, यह पूरी तरह से चलती औसत के रुझान को कवर करता है, लेकिन... क्या यह सार्थक है?

वास्तव में, एआरएमए मॉडल स्वयं गलत नहीं है, क्योंकि समस्या मॉडल स्वयं में नहीं है, बल्कि चीजों के स्वयं के उद्देश्य तर्क में है। समय श्रृंखला मॉडल केवल पिछले और बाद के अवलोकनों के बीच सहसंबंध के आधार पर स्थापित किया जा सकता है। इसलिए, सफेद शोर श्रृंखला का मॉडल बनाना असंभव है। इसलिए, सभी पिछले काम एक बोल्ड धारणा पर आधारित है कि बीटीसी की रिटर्न दर श्रृंखला स्वतंत्र और समान रूप से वितरित नहीं हो सकती है।

आम तौर पर, रिटर्न रेट श्रृंखलाएं मार्टिंगेल अंतर श्रृंखलाएं हैं, जिसका अर्थ है कि रिटर्न दर अप्रत्याशित है, और संबंधित बाजार की कमजोर दक्षता धारणा बरकरार है। हमने माना है कि व्यक्तिगत नमूनों में रिटर्न दरों में एक निश्चित डिग्री का ऑटोकोरेलेशन है, और उसी वितरण धारणा को प्रशिक्षण सेट पर लागू करने के लिए मिलान मॉडल को लागू करना भी है, ताकि एक सरल एआरएमए मॉडल मिलान किया जा सके, जिसमें खराब भविष्य कहने वाला प्रभाव होना तय है।

हालांकि, मेल खाने वाला अवशिष्ट अनुक्रम भी एक मार्टिंगेल अंतर अनुक्रम है। मार्टिंगेल अंतर अनुक्रम स्वतंत्र और समान रूप से वितरित नहीं हो सकता है, लेकिन सशर्त विचलन पिछले मूल्य पर निर्भर हो सकता है, इसलिए प्रथम-क्रम ऑटोकोरेलेशन चला गया है, लेकिन अभी भी उच्च-क्रम ऑटोकोरेलेशन है, जो कि उतार-चढ़ाव को मॉडलिंग और अवलोकन करने के लिए एक महत्वपूर्ण शर्त भी है।

यदि ऐसा तर्क सही है, तो विभिन्न अस्थिरता मॉडल के निर्माण का आधार भी सही है। इसलिए रिटर्न दर श्रृंखला के लिए, यदि एक कमजोर कुशल बाजार संतुष्ट है, तो औसत मूल्य की भविष्यवाणी करना मुश्किल होना चाहिए, लेकिन विचलन अनुमानित है। और मिलान किया गया एआरएमए एक उचित गुणवत्ता समय श्रृंखला बेंचमार्क प्रदान करता है, तो गुणवत्ता अस्थिरता भविष्यवाणी की गुणवत्ता को भी निर्धारित करती है।

अंत में, आइए भविष्यवाणी के प्रभाव का मूल्यांकन सरलता से करें। मूल्यांकन बेंचमार्क के रूप में त्रुटि के साथ, नमूने के अंदर और बाहर के संकेतक इस प्रकार हैंः

[15] मेंः

start = '2020-02-14 00:00:00+08:00'
predicts_ARIMA_normal = model_results.get_prediction(dynamic=False)
predicts_ARIMA_dynamic = model_results.get_prediction(dynamic=True)
training_label = 'log_return'

compare_ARCH_X = pd.DataFrame()
compare_ARCH_X['Model'] = ['NORMAL','DYNAMIC']
compare_ARCH_X['RMSE'] = [rmse(predicts_ARIMA_normal.predicted_mean[1:], kline_test[training_label][:826]),
                          rmse(predicts_ARIMA_dynamic.predicted_mean[1:], kline_test[training_label][:826])]
compare_ARCH_X['MAPE'] = [mape(predicts_ARIMA_normal.predicted_mean[:50], kline_test[training_label][:50]),
                          mape(predicts_ARIMA_dynamic.predicted_mean[:50], kline_test[training_label][:50])]
compare_ARCH_X

बाहर[15]: मूल औसत वर्ग त्रुटि (आरएमएसई): 0.0184 मूल औसत वर्ग त्रुटि (आरएमएसई): 0.0167 औसत पूर्ण प्रतिशत त्रुटि (एमएपीई): 2.25e+03 औसत पूर्ण प्रतिशत त्रुटि (एमएपीई): 395

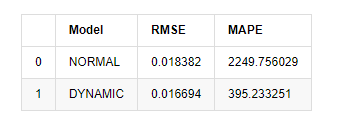
यह देखा जा सकता है कि स्थिर मॉडल पूर्वानुमानित मूल्य और वास्तविक मूल्य के बीच त्रुटि संयोग के मामले में गतिशील मॉडल से थोड़ा बेहतर है। यह बिटकॉइन की लघुगणकीय रिटर्न दर से अच्छी तरह मेल खाता है, जो मूल रूप से अपेक्षाओं के अनुरूप है। गतिशील भविष्यवाणी में अधिक सटीक चर जानकारी की कमी है, और त्रुटि को पुनरावृत्ति द्वारा भी बढ़ाया जाता है, इसलिए भविष्यवाणी प्रभाव खराब है। MAPE 100% से अधिक है, इसलिए दोनों मॉडल की वास्तविक मिलान गुणवत्ता आदर्श नहीं है।

[18] मेंः

predict_step = 50
predicts_ARIMA_normal_out = model_results.get_forecast(steps=predict_step, dynamic=False)
predicts_ARIMA_dynamic_out = model_results.get_forecast(steps=predict_step, dynamic=True)
testing_ts = kline_test
training_label = 'log_return'

compare_ARCH_X = pd.DataFrame()
compare_ARCH_X['Model'] = ['NORMAL','DYNAMIC']
compare_ARCH_X['RMSE'] = [get_rmse(predicts_ARIMA_normal_out.predicted_mean, testing_ts[training_label]),
                          get_rmse(predicts_ARIMA_dynamic_out.predicted_mean, testing_ts[training_label])]
compare_ARCH_X['MAPE'] = [get_mape(predicts_ARIMA_normal_out.predicted_mean, testing_ts[training_label]),
                          get_mape(predicts_ARIMA_dynamic_out.predicted_mean, testing_ts[training_label])]
compare_ARCH_X

बाहर[18]:

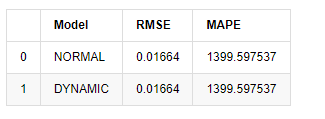
चूंकि नमूना के बाहर अगली भविष्यवाणी पिछले चरण के परिणामों पर निर्भर करती है, इसलिए केवल गतिशील मॉडल प्रभावी है। हालांकि, गतिशील मॉडल का दीर्घकालिक त्रुटि दोष समग्र मॉडल की अपर्याप्त भविष्यवाणी क्षमता का कारण बनता है, इसलिए अगले चरण की भविष्यवाणी अधिकतम होती है।

संक्षेप में, एआरएमए मॉडल स्टेटिक मॉडल बिटकॉइन के रिटर्न की इंट्रा सैंपल दर से मेल खाने के लिए उपयुक्त है। रिटर्न की दर की अल्पकालिक भविष्यवाणी आत्मविश्वास अंतराल को प्रभावी ढंग से कवर कर सकती है, लेकिन दीर्घकालिक भविष्यवाणी बहुत मुश्किल है, जो बाजार की कमजोर प्रभावशीलता को पूरा करती है। परीक्षण के बाद, नमूना अंतराल के भीतर रिटर्न दर बाद में अस्थिरता अवलोकन की शर्त को पूरा करती है।

5. आर्क प्रभाव

ARCH मॉडल प्रभाव सशर्त heteroscedasticity अनुक्रम का श्रृंखला सहसंबंध है। मिश्रण परीक्षण Ljung बॉक्स का उपयोग यह निर्धारित करने के लिए किया जाता है कि क्या ARCH प्रभाव है। यदि ARCH प्रभाव परीक्षण पारित किया जाता है, अर्थात श्रृंखला में heteroscedasticity है, तो GARCH मॉडलिंग का अगला चरण संयुक्त रूप से औसत समीकरण और अस्थिरता समीकरण का अनुमान लगाने के लिए किया जा सकता है। अन्यथा, मॉडल को अनुकूलित और पुनः समायोजित करने की आवश्यकता होती है, जैसे कि अंतर प्रसंस्करण या पारस्परिक श्रृंखला।

हम यहाँ कुछ डेटा सेट और वैश्विक चर तैयार करते हैंः

[33] मेंः

count_num = 100000
start_date = '2020-03-01'

df = get_bars('huobi.btc_usdt', '1m', count=count_num, start=start_date)  # Take the minute data
kline_1m = pd.DataFrame(df['close'], dtype=np.float)
kline_1m.index.name = 'date'
kline_1m['log_price'] = np.log(kline_1m['close'])
kline_1m['return'] = kline_1m['close'].pct_change().dropna()
kline_1m['log_return'] = kline_1m['log_price'] - kline_1m['log_price'].shift(1)

kline_1m['squared_log_return'] = np.power(kline_1m['log_return'], 2)

kline_1m['return_100x'] = np.multiply(kline_1m['return'], 100)
kline_1m['log_return_100x'] = np.multiply(kline_1m['log_return'], 100)  # Enlarge 100 times

df = get_bars('huobi.btc_usdt', '1h', count=count_num, start=start_date)  # Take the hour data
kline_test = pd.DataFrame(df['close'], dtype=np.float)
kline_test.index.name = 'date'
kline_test['log_price'] = np.log(kline_test['close'])  # Calculate the daily logarithmic rate of return
kline_test['return'] = kline_test['log_price'].pct_change().dropna()
kline_test['log_return'] = kline_test['log_price'] - kline_test['log_price'].shift(1)  # Calculate the logarithmic rate of return
kline_test['squared_log_return'] = np.power(kline_test['log_return'], 2)  # Exponential square of log daily return rate

kline_test['return_100x'] = np.multiply(kline_test['return'], 100)
kline_test['log_return_100x'] = np.multiply(kline_test['log_return'], 100)  # Enlarge 100 times

kline_test['realized_variance_1_hour'] = kline_1m.loc[:, 'squared_log_return'].resample('h', closed='left', label='left').sum().copy() # Resampling to days 
kline_test['realized_volatility_1_hour'] = np.sqrt(kline_test['realized_variance_1_hour'])  # Volatility of variance derivation

kline_test = kline_test[4:-2500]
kline_test.head(3)

बाहर[33]:

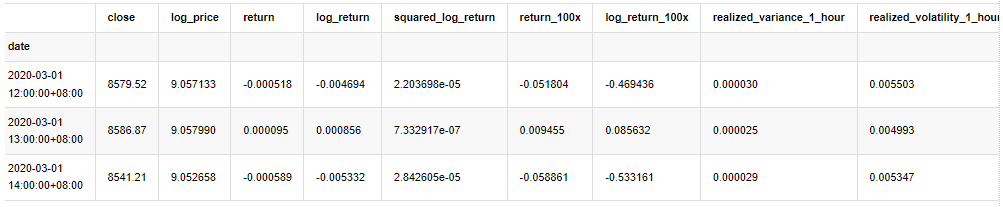
[22] मेंः

cc = 3
model_p = 1
predict_lag = 30
label = 'log_return'

training_label = label
training_ts = pd.DataFrame(kline_test[training_label], dtype=np.float)

training_arch_label = label
training_arch = pd.DataFrame(kline_test[training_arch_label], dtype=np.float)

training_garch_label = label
training_garch = pd.DataFrame(kline_test[training_garch_label], dtype=np.float)

training_egarch_label = label
training_egarch = pd.DataFrame(kline_test[training_egarch_label], dtype=np.float)

training_arch.plot(figsize = (18,4))

बाहर[22]:

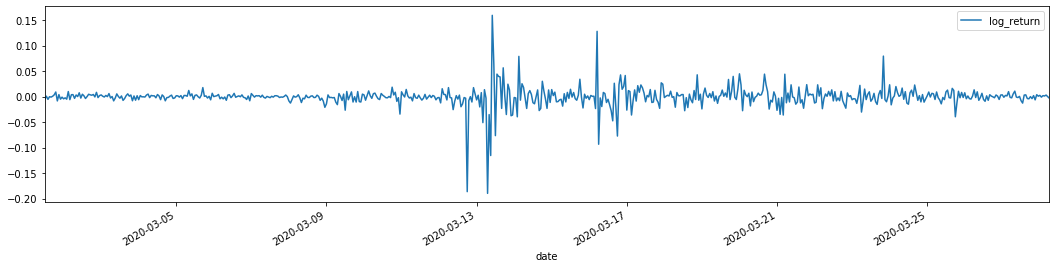
ऊपर लॉगरिथम रिटर्न दरें दिखाई गई हैं। इसके बाद, हमें नमूना के आर्क प्रभाव का परीक्षण करने की आवश्यकता है। हम ARMA के आधार पर नमूना के भीतर अवशिष्ट श्रृंखला स्थापित करते हैं। कुछ श्रृंखलाओं और अवशिष्ट और अवशिष्ट की वर्ग श्रृंखला की गणना पहले की जाती हैः

[20] मेंः

training_arma_model = smt.SARIMAX(endog=training_ts, trend='c', order=(0, 0, 1), seasonal_order=(0, 0, 0, 0))
arma_model_results = training_arma_model.fit(disp=False)
arma_model_results.summary()
training_arma_fitvalue = pd.DataFrame(arma_model_results.fittedvalues,dtype=np.float)
at = pd.merge(training_ts, training_arma_fitvalue, on='date')
at.columns = ['log_return', 'model_fit']
at['res'] = at['log_return'] - at['model_fit']
at['res2'] = np.square(at['res'])
at.head()

बाहर[20]:

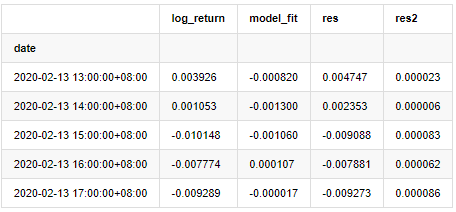
फिर नमूना की शेष श्रृंखला को ग्राफ किया जाता है।

[69] मेंः

fig, ax = plt.subplots(figsize=(18, 6))
ax1 = fig.add_subplot(2,1,1)
at['res'][1:].plot(ax=ax1,label='resid')
plt.legend(loc='best')

ax2 = fig.add_subplot(2,1,2)
at['res2'][1:].plot(ax=ax2,label='resid2')

plt.legend(loc='best')
plt.tight_layout()
sns.despine()

बाहर[69]:

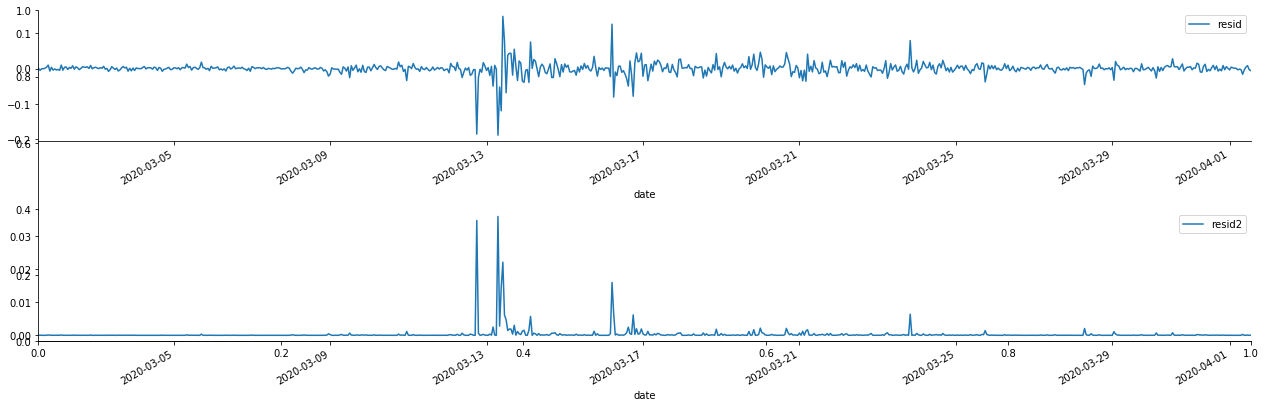
यह देखा जा सकता है कि अवशिष्ट श्रृंखला में स्पष्ट संचयन विशेषताएं हैं, और यह शुरू में न्याय किया जा सकता है कि श्रृंखला में आर्क प्रभाव है। एसीएफ को वर्ग अवशेषों के ऑटोकोरेलेशन का परीक्षण करने के लिए भी लिया जाता है, और परिणाम निम्नानुसार हैं।

[70] मेंः

figure = plt.figure(figsize=(18,4))
ax1 = figure.add_subplot(111)
fig = sm.graphics.tsa.plot_acf(at['res2'],lags = 40, ax=ax1)

बाहर[70]:

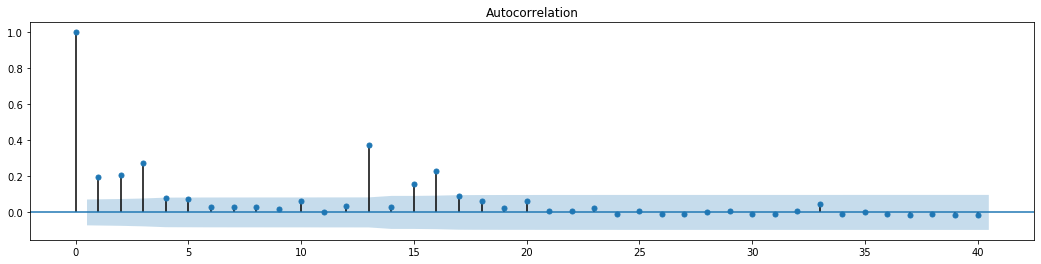
श्रृंखला मिश्रण परीक्षण के लिए मूल धारणा यह है कि श्रृंखला में कोई सहसंबंध नहीं है। यह देखा जा सकता है कि डेटा के पहले 20 आदेशों के अनुरूप पी मूल्य 0.05% आत्मविश्वास स्तर के महत्वपूर्ण मूल्य से कम हैं। इसलिए, मूल धारणा को खारिज कर दिया जाता है, अर्थात श्रृंखला के अवशिष्ट में एआरसीएच प्रभाव है। शेष श्रृंखला की हेटरोसेडेस्टिसिटी को फिट करने और अस्थिरता की भविष्यवाणी करने के लिए एआरसीएच प्रकार मॉडल के माध्यम से विचलन मॉडल स्थापित किया जा सकता है।

6. गार्च मॉडलिंग

GARCH मॉडलिंग करने से पहले, हमें श्रृंखला के मोटी पूंछ भाग से निपटने की आवश्यकता है। क्योंकि परिकल्पना में श्रृंखला का त्रुटि शब्द सामान्य वितरण या टी वितरण के अनुरूप होना चाहिए, और हमने पहले सत्यापित किया है कि उपज श्रृंखला में मोटी पूंछ वितरण है, इसलिए हमें इस भाग का वर्णन और पूरक करने की आवश्यकता है।

गार्च मॉडलिंग में, त्रुटि आइटम सामान्य वितरण, टी-वितरण, जीईडी (सामान्य त्रुटि वितरण) वितरण और स्केवेड स्टूडेंट्स टी-वितरण के विकल्प प्रदान करता है। एआईसी मानदंडों के अनुसार, हम सभी विकल्पों के परिणामों की तुलना करने के लिए गिनती संयुक्त प्रतिगमन अनुमान का उपयोग करते हैं, और जी की सर्वोत्तम मिलान डिग्री प्राप्त करते हैं।

संबंधित

अधिक