8つの機械学習アルゴリズムの比較
 0
0
 6878
6878
8つの機械学習アルゴリズムの比較
この記事では,以下のいくつかの一般的なアルゴリズムの適応シナリオと,その優劣を概要として取り上げます.
機械学習アルゴリズムは,分類,回帰,集積,推薦,画像認識の領域などに多すぎて,適切なアルゴリズムを見つけるのは本当に簡単ではありません.
通常は,SVM,GBDT,Adaboostのような,一般的に受け入れられるアルゴリズムで始めます. ディープラーニングは熱い時代であり,ニューラルネットワークも良い選択です.
精度 (accuracy) を気にするなら,最も良い方法は,各アルゴリズムを”つずつテストし,比較し,パラメータを調整して,各アルゴリズムが最適解にたどり着くようにして,最後に最良のアルゴリズムを選択することです.
しかし,もしあなたが問題解決に十分なアルゴリズムを 探しているだけなら,あるいは,ここでは,いくつかのヒントを参考にすると,以下の各アルゴリズムのメリットとデメリットを分析して,そのメリットとデメリットを基に,より簡単に選択することができます.
- ## 偏差と差
統計学では,モデルが良いのか悪いのか, 偏差と差異によって測定されます. 偏差と差異を一般化しましょう.
偏差:予測値 (推定値) の期待値Eと実際の値Yの間の差を記述する.偏差が大きいほど,実際のデータから離れている.
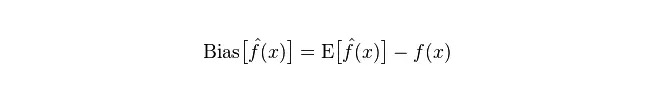
偏差:予測値Pの変化範囲を記述し,分散度,予測値の偏差,すなわちその期待値Eからの距離である.偏差が大きいほど,データの分布が分散する.
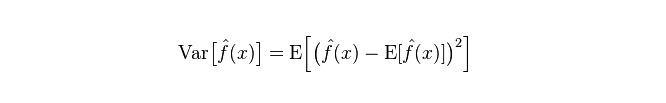
モデルの実際の誤差は,以下の2つの合計である.
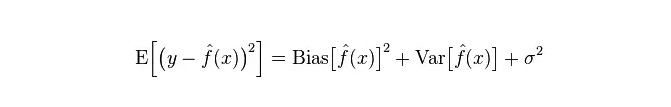
小型のトレーニングセットの場合,高偏差/低差差の分類器 (例えば,素朴なベイエスNB) は,低偏差/高差の大型分類器 (例えば,KNN) よりも優れている (後者は過適合する).
しかし,トレーニングセットが大きくなるにつれて,モデルが原始データに対する予測能力が良くなるほど,偏差は小さくなり,低偏差/高差分类器は徐々に優位性を発揮し始めます (それらはより低い漸進的誤差を持っているため),高偏差分類器は,この時点で正確なモデルを提供するのに不十分です.
もちろん,これは生成モデル (NB) と判定モデル (KNN) の違いだと考えてもいいでしょう.
- ## バイアスは,高偏差低偏差で,なぜ素朴なのか?
この記事の引用はこちらから.
まず,トレーニングセットとテストセットの関係を知っていると仮定します. 簡単に言えば,トレーニングセットでモデルを学習し,テストセットでテストします. テストセットの誤差率によって効果が測定されます.
しかし,多くの場合,テストセットとトレーニングセットが同じデータ分布に適合していると仮定するだけで,実際のテストデータを得ることはできません.
訓練サンプルが少ないため (少なくとも十分ではない),訓練集で得られたモデルは,決して本当に正確ではない。 (訓練集で100%の正確さでも,それが真のデータ分布を刻画しているとは言えません.真のデータ分布を刻画するのが目的であり,訓練集の限られたデータポイントを刻画するだけではありません).
また,実態では,トレーニングサンプルはしばしばノイズ誤差があるので,トレーニングセットの完璧さに過度にこだわりすぎると,非常に複雑なモデルを採用すると,モデルがトレーニングセット内の誤差をすべて実際のデータ分布特征として考えさせ,誤ったデータ分布推定が得られます.
この場合,実際のテストセットでは間違いが一目瞭然になる (この現象は合致と呼ばれている).しかし,あまりにも単純なモデルも使用することはできない.そうでなければ,データ分布が比較的複雑であるとき,モデルはデータを描き出すのに十分でない (訓練セットでも誤差率が高く,この現象は合致が欠けている).
過適合は,採用されたモデルが実際のデータ分布よりも複雑であることを示す.過適合は,採用されたモデルが実際のデータ分布よりも単純であることを示す.
統計学的な学習の枠組みで,モデル複雑さを描画する際には,Error = Bias + Varianceという見解がある.ここでのErrorは,おそらくモデルの予測誤差として理解できる.これは,2つの部分で構成され,一部はモデルがあまりにも単純であるために推定が不正確である部分 ((Bias)),もう一部はモデルがあまりにも複雑であるためにもたらされるより大きな変化空間と不確実性である部分 ((Variance) である.
したがって,単純ベアスを分析するのは容易である.その単純な仮定は,各データの間の関係が関係なく,非常に簡素化されたモデルである.したがって,このような単純なモデルに対して,ほとんどの場合,Bias部分はVariance部分よりも大きい,つまり高偏差が低方差である.
実際には,エラーを最小限にするために,モデルを選択する際にBiasとVarianceの割合をバランスする必要があります.つまり,over-fittingとunder-fittingをバランスする必要があります.
偏差と方差の関係とモデルの複雑さは,以下の図でより明確になります.
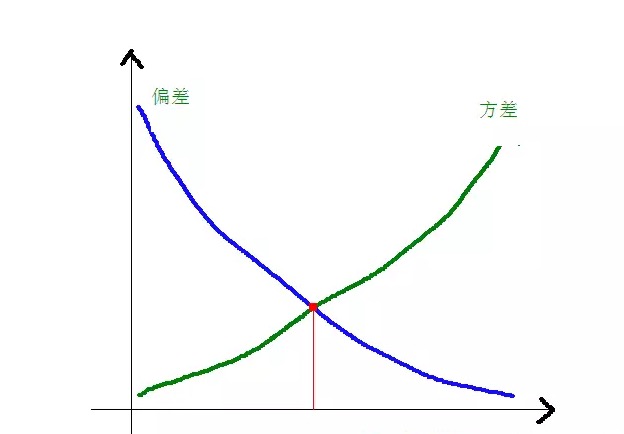
モデルが複雑になるにつれ,偏差は小さくなり,差は大きくなる.
-
一般的なアルゴリズムのメリット・デメリット
- ### 1. 素朴なベイス
単純ベージは生成型モデル (生成型モデルと判定型モデルについて,主に,合同分布を要求するかどうか) に属し,非常に単純で,あなたはただ数値の山を計算するだけです.
条件付き独立性仮説 (((より厳格な条件) を加えた場合,素朴なベージアン分類器の収束速度は,論理回帰のような判別モデルより速くなり,それゆえ,訓練データより少ないだけが必要になります.NB条件付き独立性仮説が成立しないとしても,NB分類器は実用的には依然として優れたパフォーマンスを発揮します.
mRMRのRは,特性の冗長性である. 典型的な例を引用すると,例えば,あなたがブラッド・ピットとトム・クルーズの映画が好きであるにもかかわらず,彼らが一緒に演じる映画を嫌いなことを学ぶことはできません.
利点:
素朴なベアスのモデルは,古典的な数学理論に由来し,堅固な数学基盤と安定した分類効率を有する. 小規模なデータに対して良好な性能で,複数のカテゴリーに属するタスクを1つずつ処理し,増量訓練に適しています. 欠落したデータにはあまり敏感ではなく,アルゴリズムも比較的シンプルで,しばしばテキスト分類に使用される. デメリット:
予測可能性の計算が必要になります クラシファケーションの誤差率 入力データの表現形式に敏感である.
- ### 2. 論理回帰
L0,L1,L2,etc) のような方法があり, 素朴なベアスのように,自分の特性が関連しているかどうか心配する必要はありません.
意思決定ツリーとSVMマシンに比べると,良い確率解釈が得られ,新しいデータを使ってモデルを簡単に更新することもできます.
確率構造が必要な場合 (例えば,分類の値を単純に調整したり,不確実性を指摘したり,信頼区間を得たい場合) または,より多くのトレーニングデータを後でモデルに迅速に統合したい場合は,それを使用してください.
シグモイド関数:
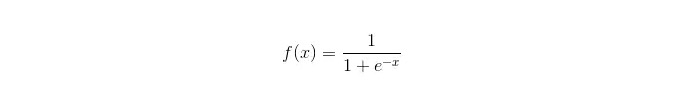
利点: シンプルで広く産業用の問題に 適用される コンピュータは,コンピュータを分類する際に,非常に小さな計算量,高速,低ストレージで処理します. 簡単な観測サンプル確率スコア 論理回帰においては,多重共線性とは問題ではなく,L2正規化と組み合わせてその問題を解決することができる. デメリット: 特性空間が大きいとき,論理回帰の性能はよくない. 適格性や正確性には欠けやすい 複数の特徴や変数をうまく処理できない. 2つの分類問題しか処理できない (この基礎から派生したsoftmaxは複数の分類に使用できる) であり,線形的に分ける必要がある. 非線形特征については,変換が必要です.
- ### 3. 線形回帰
線形回帰は,Logistic回帰とは異なり回帰に用いられ,その基本的考え方は,梯度下降法を使用して最小二乗法形式の誤差関数を最適化することであり,当然,通常の equation で直接参数を求めることもできます.結果として:
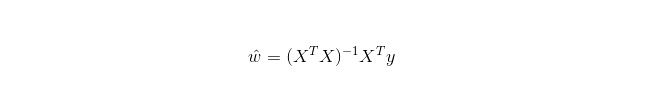
LWLRでは,パラメータの計算式は次のとおりです.
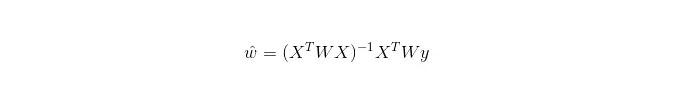
LWLRはLRとは異なり,リグレーション計算を行うたびに訓練サンプルを少なくとも1回巡るので,LWLRは非パラメータモデルである.
優点: 実行しやすく,計算しやすく
デメリット: 非線形データにマッチングできない.
- ### 4. 近隣アルゴリズムのKNN
KNNは近隣アルゴリズムであり,その主要プロセスは:
トレーニングサンプルとテストサンプルの各サンプルの距離を計算する (一般的な距離測定は,ヨーロッパ式距離,マース距離などである).
上のすべての距離値を並べます.
選択した最初の k の最小距離のサンプル;
このk個の標識を投票して,最終的な分類を決定します.
最適なK値の選択は,データによって決まります.通常,分類時に大きなK値は騒音の影響を軽減できます.しかし,カテゴリー間の境界は曖昧になります.
よりよいK値は,様々な啓蒙型技術によって得られます.例えば,交差検証.さらに,ノイズと非関連性特性のベクトルの存在は,K近隣アルゴリズムの正確性を低下させます.
近隣アルゴリズムは強い一致性結果を有する.データが無限に近づくにつれて,アルゴリズムはベイエスのアルゴリズムの誤差率の2倍を超えないことを保証する.いくつかの良いK値に対して,Kの近隣はベイエスの理論的誤差率を超えないことを保証する.
KNNアルゴリズムの優位性
理論は成熟し,考えはシンプルで,分類にも,帰還にも使える. 非線形分類に用いられる. 訓練時間複合度はO (n) である. データの仮定はなく,正確さも高く,アウトリヤーには敏感ではありません. 欠点
計算量も大きい サンプルの不均衡の問題 ((つまり,あるカテゴリーのサンプルの数は多く,他のサンプルの数は少ない) コンピュータのメモリが多すぎる
- ### 5. 意思決定ツリー
解釈しやすい.特征間の相互作用をストレスのない方法で処理し,非パラメータ化されるため,異常値やデータの線形分離を心配する必要はありません.例えば,決定木は,カテゴリーAが特征次元xの端で,カテゴリーBが中間で,そしてカテゴリーAが特征次元xの前端で簡単に処理できます.
オンライン学習ができないという欠点があるため,新しいサンプルが到着すると,決定樹は完全に再構築される.
もう一つの欠点は,過適合が容易であることです. しかし,これはランダムな森林RF (またはブーストツリー) のような統合方法の切開点です.
また,ランダムフォレストは,多くの分類問題の勝者であり (通常は,サポートベクトルマシンの好みより少し),トレーニングが速く,調整可能であり,サポートベクトルマシンのようにパラメータを大量に変更する必要がないので,以前から人気がありました.
意思決定ツリーの重要なポイントは, 属性を分岐に選択することです. だから,情報増益の計算式に注意して,それを深く理解してください.
計算式は以下のとおりです.
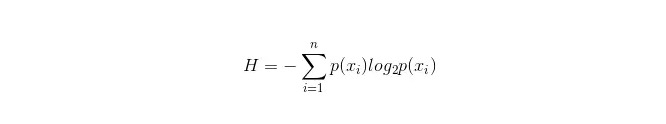
このnは,nの分類分類を代表する ((例えば,2種類の問題であるとするなら,n=2) である。2種類のサンプルが,総サンプルにそれぞれ現れる確率p1とp2を計算することで,未選択の属性分岐前の情報を計算することができる。
現在,属性xixiを選択して,枝分かれを行う.このとき,枝分かれの規則は,xi=vxi=vの場合,サンプルを木の一つの枝に分け,不等しい場合は別の枝に入ります.
明らかに,分岐中のサンプルは2つのカテゴリーを含む可能性が高い.分岐後の総情報H =p1 H1+p2 H2を計算し,このときの情報増益ΔH = H - Hを計算する.情報増益を原則として,すべての属性をテストして,この次は分岐属性として最も増益する属性を選択する.
意思決定ツリーそのものの利点
計算はシンプルで分かりやすく,説明が簡単です. 欠落した属性を持つサンプルを比較する 関連性のない特徴を処理する能力 比較的短時間で,大規模なデータソースに対して,実行可能で効果的な結果が得られる. 欠点
過剰適合が起こりやすい (ランダムな森林は過剰適合を大幅に減らすことができる) 関連性を見落として, 各カテゴリーでサンプル数が不一致するデータに対して,決定樹の中で,情報増益の結果は,より多くの数値を持つ特性を有するものに偏っている (RFのように,情報増益を使用する限り,このデメリットがあります).
- ### 5.1 Adaboosting
Adaboostは,加算モデルであり,それぞれのモデルは前のモデルの誤差率に基づいて構築され,誤差分別したサンプルに過度に注意を向け,正しく分類されたサンプルに注意を減らして,繰り返し繰り返すことで,比較的良いモデルが得られる.典型的なブーଷ୍ଟିングアルゴリズムである.以下は,その長所と短所を要約する.
アドバンテージ
adaboostは,高度な精度を持つ分類器である. Adaboost アルゴリズムは,フレームワークを提供する. 単純な分類器を使用すると,計算された結果は理解可能であり,弱い分類器の構成は極めて単純である. シンプルで,特性を選別する必要はありません. オーバーフィッティングは起こりません. ランダムフォレストやGBDTなどの組み合わせアルゴリズムについては,この記事を参照してください: 機械学習 - 組み合わせアルゴリズムの概要
デメリット:アウトリエに敏感
- ### 6. SVM 支援ベクトルマシン
高精度で,過適合を避けるための優れた理論的保証を提供し,また,データが原特征空間において線形的に分割できないとしても,適切な核関数を与えれば,それはうまく動作する.
動超高次元のテキスト分類の問題で特に人気がある。残念ながらメモリが消費され,解釈が困難であり,動作と参数付けも少し面倒である.しかし,ランダムフォレストは,これらの欠点を回避して,より実用的である。
アドバンテージ 巨大な特征空間という高次元の問題を解くことができます. 非線形特性の相互作用を処理する能力 データを全て頼りにする必要はありません. グローバル化のための能力の向上
欠点 実験の成果は,多くのサンプルを採取したときに得られることがありません. 非線形の問題には普遍的な解決法がないため,適切な核関数を見つけるのは時として困難である. データの欠落に敏感です libsvmには4種類のカーネルの関数がある: 線形カーネル,多項式カーネル,RBF,およびシグモイドカーネル):
“つ目は,サンプル数が特徴数より少ない場合,非線形核を選ばなくなり,単に線形核を使うこと.
2つ目は,標本数が特徴数より多い場合,非線形核を用いて標本をより高い次元にマッピングすることで,一般的によりよい結果が得られる.
第三に,サンプル数と特征数の等しい場合,非線形核を用いることができ,原理は第2種と同じである。
最初のケースでは,データを減量して,非線形核を使用することもできます.
- ### 7. 人工ニューラルネットワークのメリット・デメリット
人工ニューラルネットワークの利点: クラシファケーションの正確さ コンピュータは, コンピュータが, コンピュータが, コンピュータが, 騒音神経に対する強烈な頑丈性と容認力があり,複雑な非線形関係に十分に近付くことができる. 記憶の機能がある.
人工ニューラルネットワークの欠点: ニューラルネットワークは,ネットワークのトポグラフィー構造,重み値,値の初期値などの多くのパラメータを必要とします. 学習過程を観察できないことや,結果の解釈が難しいことが,結果の信頼性や可視性に影響する. 学習の時間が長くなり,学習の目的には及ばないかもしれません.
- ### 8 K-Means クラグリング
K-Meansのクラグリングに関する記事を書いたことがあります. K-Meansの推論には,非常に強力なEM思想があります.
アドバンテージ アルゴリズムはシンプルで実行しやすい. 大量のデータセットを扱う場合,このアルゴリズムは比較的スケーラブルで高効率である.このアルゴリズムの複雑さは,nがすべてのオブジェクトの数,kがの数,tが繰り返しの数であるため,約O{\displaystyle \O{\displaystyle \O{\displaystyle \O{\displaystyle \O{\mathrm {n}} }) である.通常,k<は密集し,球状または球状であり,との間の区別が明確である場合,聚類効果は優れています.
欠点 数値型データに適したデータ型に対する高い要求; 局所的な最小値に収束する可能性があり,大規模なデータでは収束が遅い K値は比較的に難しい. 初期値の値に敏感で,異なる初期値に対して,異なる集群結果を引き起こす可能性がある. の形状が凸でないや,大きさが大きく異なるには適さない. のノイズと孤立点データに敏感な,少量のこの種のデータは,平均値に大きな影響を及ぼします.
アルゴリズムによる参照選択
翻訳の仕方について,簡単なアルゴリズムの選択のヒントを紹介した記事があります.
まず最初に選択すべきは,論理回帰であり,その効果があまり良くない場合,その結果を基準として参照し,その基礎で他のアルゴリズムと比較することができる.
モデル性能を大幅に向上させられるかを見るために,意思決定ツリー (ランダムな森林) を試す. 最終的に最終的なモデルとして使用しない場合でも,ノイズ変数を削除し,特性を選択するためにランダムな森林を使用することができます.
特徴の数と観測サンプルが特に多い場合,資源と時間が充足しているときに (これは重要な前提である) SVMを使用することは必ず選択肢である.
通常の場合:GBDT>=SVM>=RF>=Adaboost>=Other…,今はディープラーニングが熱い,多くの分野で使用されている,それはニューラルネットワークに基づいている,現在私も勉強している,ただ理論的な知識はあまり厚くない,理解は深くない,ここでは紹介しない。
アルゴリズムは重要ですが,良いデータは良いアルゴリズムよりも優れているため,優れた設計特性が非常に有益です.もしあなたが超大量のデータセットを持っているなら,あなたがどのアルゴリズムを使用しても,分類の性能にはあまり影響がないかもしれません (この時点で,速度と使いやすさに基づいて選択することができます).
-
参考文献