Pengelas Bayesian berdasarkan algoritma KNN

Asas teori untuk merancang penjenamaan untuk membuat keputusan klasifikasi Teori Keputusan Bayesian:

Perbandingan P(ωi 11:1x) ⋅ di manaωi adalah kelas i, x adalah data yang telah diperhatikan dan dikelaskan, P(ωi 11:1x) menunjukkan berapa besar kebarangkalian untuk menentukan bahawa ia tergolong dalam kelas i dalam keadaan vektor ciri yang diketahui dari data ini, yang juga menjadi kebarangkalian penyesuaian. Berdasarkan formula Bayes, ia boleh dinyatakan sebagai:

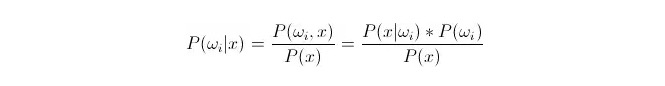
Di antaranya, P (x) dipanggil kebarangkalian kesamaan atau kebarangkalian bersyarat; P (ω) dipanggil kebarangkalian terdahulu, kerana tidak berkaitan dengan percubaan dan boleh diketahui sebelum percubaan.

Dalam pengelompokan, diberikan x, pilihlah kategori yang menjadikan kebarangkalian pengesahan balik P ((ωiⴰⵙx) terbesar. Dalam perbandingan setiap kategori, apabila P ((ωiⴰⵙx) kecil,ωi adalah variabel, dan x adalah tetap; jadi P ((x) boleh dihapuskan dan tidak dipertimbangkan.

Jadi ia akan menjadi P (x) = P (x) = P (i)*P ((ωi) soalan ▽) Kebarangkalian terdahulu P ((ωi) adalah baik, asalkan peratusan data yang muncul di bawah setiap klasifikasi tertumpu pada latihan statistik.

Mungkin peluang P ((x Berdosaωi) akan menjadi rumit, kerana x adalah data dalam set ujian, dan tidak dapat diperoleh secara langsung dari set latihan. Oleh itu, kita perlu mencari peraturan pengedaran data dalam set latihan, dan kemudian kita akan mendapat P ((x Berdosaωi).

Berikut adalah k algoritma berdekatan, dalam bahasa Inggeris adalah KNN.

Kita perlu menyesuaikan pembahagian data dalam kumpulan latihan berdasarkan data x1, x2…xn (di mana setiap data adalah dimensi m), di bawah kategoriωi. Berikan x sebagai titik mana-mana dalam ruang dimensi m, bagaimana untuk mengira P(x bagiωi)?

Kita tahu bahawa apabila jumlah data cukup besar, kita boleh menggunakan kebarangkalian perkadaran. Menggunakan prinsip ini, di sekitar titik x, carilah titik sampel k yang terdekat dari jarak titik x, di mana ada yang tergolong dalam kategori i.

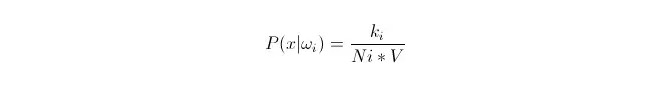
Kita boleh lihat bahawa kita telah mengira kepadatan kebarangkalian berkondisi pada titik x.

P (ωi) bagaimana? Berdasarkan kaedah di atas, P ((ωi) = Ni/N 。 di mana N adalah jumlah sampel。 Dan P (x) = k/N.*V), di mana k adalah bilangan semua titik sampel yang mengelilingi superbola ini; N adalah jumlah sampel. Jadi, P (ωi kesinambungan) boleh dikira:

P(ωi|x)=ki/k

Untuk menerangkan persamaan di atas, dalam sebuah superbola berukuran V, terdapat k sampel yang dikelilingi, di antaranya terdapat ki yang tergolong dalam kelas i. Dengan cara ini, sampel mana yang dikelilingi paling banyak, kita dapat menentukan di sini x yang sepatutnya tergolong dalam kelas mana. Ini adalah pengelompokan yang direka dengan k algoritma berdekatan.