Modelagem e análise da volatilidade do Bitcoin com base no modelo ARMA-EGARCH

Recentemente, fiz alguma análise sobre a volatilidade do Bitcoin, que é verbal e espontânea. Então eu simplesmente compartilho parte do meu entendimento e código da seguinte forma. Minha capacidade é limitada, e o código não é muito perfeito. Se houver algum erro, por favor, aponte e corrija diretamente.

1. Uma breve descrição das séries temporais das finanças

A série temporal de finanças é um conjunto de modelos de série de processos estocásticos baseados em uma variável observada na dimensão temporal. A variável é geralmente a taxa de retorno dos ativos.

Aqui, presume-se ousadamente que a taxa de retorno do Bitcoin esteja em conformidade com as características da taxa de retorno dos ativos financeiros gerais, ou seja, é uma série fraca e suave, que pode ser demonstrada por testes de consistência de várias amostras.

Preparados, bibliotecas de importação, funções de encapsulamento

A configuração do ambiente de pesquisa está completa. A biblioteca necessária para cálculos subsequentes é importada aqui. Uma vez que é escrita intermitentemente, pode ser redundante. Por favor limpe-a por si mesmo.

Em [1]:

'''
start: 2020-02-01 00:00:00
end: 2020-03-01 00:00:00
period: 1h
exchanges: [{"eid":"Huobi","currency":"BTC_USDT","stocks":0}]
'''
from __future__ import absolute_import, division, print_function
from fmz import * # Import all FMZ functions
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.lines as mlines
import seaborn as sns
import statsmodels.api as sm
import statsmodels.formula.api as smf
import statsmodels.tsa.api as smt
from statsmodels.graphics.api import qqplot
from statsmodels.stats.diagnostic import acorr_ljungbox as lb_test
from scipy import stats
from arch import arch_model
from datetime import timedelta
from itertools import product
from math import sqrt
from sklearn.metrics import r2_score, mean_absolute_error, mean_squared_error

task = VCtx(__doc__) # Initialization, verification of FMZ reading of historical data
print(exchange.GetAccount())

Fora[1]: (Bilanço: 10000,0, FrozenBalance: 0,0, Propriedades: 0,0, FrozenPropriedades: 0,0)

    #### Encapsulate some of the functions, which will be used later. If there is a source, see the note

Em [17]:

# Plot functions
def tsplot(y, y_2, lags=None, title='', figsize=(18, 8)):  # source code: https://tomaugspurger.github.io/modern-7-timeseries.html
    fig = plt.figure(figsize=figsize)
    layout = (2, 2)
    ts_ax   = plt.subplot2grid(layout, (0, 0))
    ts2_ax = plt.subplot2grid(layout, (0, 1))
    acf_ax  = plt.subplot2grid(layout, (1, 0))
    pacf_ax = plt.subplot2grid(layout, (1, 1))
    y.plot(ax=ts_ax)
    ts_ax.set_title(title)
    y_2.plot(ax=ts2_ax)
    smt.graphics.plot_acf(y, lags=lags, ax=acf_ax)
    smt.graphics.plot_pacf(y, lags=lags, ax=pacf_ax)
    [ax.set_xlim(0) for ax in [acf_ax, pacf_ax]]
    sns.despine()
    plt.tight_layout()
    return ts_ax, ts2_ax, acf_ax, pacf_ax

# Performance evaluation
def get_rmse(y, y_hat):
    mse = np.mean((y - y_hat)**2)
    return np.sqrt(mse)

def get_mape(y, y_hat):
    perc_err = (100*(y - y_hat))/y
    return np.mean(abs(perc_err))

def get_mase(y, y_hat):
    abs_err = abs(y - y_hat)
    dsum=sum(abs(y[1:] - y_hat[1:]))
    t = len(y)
    denom = (1/(t - 1))* dsum
    return np.mean(abs_err/denom)

def mae(observation, forecast):    
    error = mean_absolute_error(observation, forecast)
    print('Mean Absolute Error (MAE): {:.3g}'.format(error))
    return error

def mape(observation, forecast): 
    observation, forecast = np.array(observation), np.array(forecast)
    # Might encounter division by zero error when observation is zero
    error = np.mean(np.abs((observation - forecast) / observation)) * 100
    print('Mean Absolute Percentage Error (MAPE): {:.3g}'.format(error))
    return error

def rmse(observation, forecast):
    error = sqrt(mean_squared_error(observation, forecast))
    print('Root Mean Square Error (RMSE): {:.3g}'.format(error))
    return error

def evaluate(pd_dataframe, observation, forecast):
    first_valid_date = pd_dataframe[forecast].first_valid_index()
    mae_error = mae(pd_dataframe[observation].loc[first_valid_date:, ], pd_dataframe[forecast].loc[first_valid_date:, ])
    mape_error = mape(pd_dataframe[observation].loc[first_valid_date:, ], pd_dataframe[forecast].loc[first_valid_date:, ])
    rmse_error = rmse(pd_dataframe[observation].loc[first_valid_date:, ], pd_dataframe[forecast].loc[first_valid_date:, ]) 

    ax = pd_dataframe.loc[:, [observation, forecast]].plot(figsize=(18,5))
    ax.xaxis.label.set_visible(False)
    return

1-2. Vamos começar com uma breve compreensão dos dados históricos do Bitcoin

De um ponto de vista estatístico, podemos dar uma olhada em algumas características de dados do Bitcoin. Tomando a descrição de dados do ano passado como exemplo, a taxa de retorno é calculada de forma simples, ou seja, o preço de fechamento é subtraído logarítmicamente. A fórmula é a seguinte: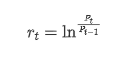

Em [3]:

df = get_bars('huobi.btc_usdt', '1d', count=10000, start='2019-01-01')
btc_year = pd.DataFrame(df['close'],dtype=np.float)
btc_year.index.name = 'date'
btc_year.index = pd.to_datetime(btc_year.index)
btc_year['log_price'] = np.log(btc_year['close'])
btc_year['log_return'] = btc_year['log_price'] - btc_year['log_price'].shift(1)
btc_year['log_return_100x'] = np.multiply(btc_year['log_return'], 100)

btc_year_test = pd.DataFrame(btc_year['log_return'].dropna(), dtype=np.float)
btc_year_test.index.name = 'date'
mean = btc_year_test.mean()
std = btc_year_test.std()
normal_result = pd.DataFrame(index=['Mean Value', 'Std Value', 'Skewness Value','Kurtosis Value'], columns=['model value'])
normal_result['model value']['Mean Value'] = ('%.4f'% mean[0])
normal_result['model value']['Std Value'] = ('%.4f'% std[0])
normal_result['model value']['Skewness Value'] = ('%.4f'% btc_year_test.skew())
normal_result['model value']['Kurtosis Value'] = ('%.4f'% btc_year_test.kurt())
normal_result

Fora[3]: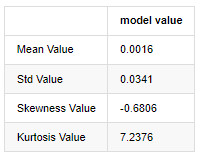

A característica das caudas grossas é que quanto mais curta a escala de tempo, mais significativa é a característica.

Tomando os dados diários de preço de fechamento de 1 de janeiro de 2019 até o presente como exemplo, fazemos uma análise descritiva de sua taxa de retorno logarítmico, e pode-se ver que a série de taxa de retorno simples do Bitcoin não está em conformidade com a distribuição normal, e tem a característica óbvia de caudas grossas.

O valor médio da sequência é de 0,0016, o desvio padrão é de 0,0341, a distorção é de -0,6819 e a curtose é de 7,2243, o que é muito maior do que a distribuição normal e tem a característica de caudas grossas.

Em [4]:

fig = plt.figure(figsize=(4,4))
ax = fig.add_subplot(111)
fig = qqplot(btc_year_test['log_return'], line='q', ax=ax, fit=True)

Fora[4]:

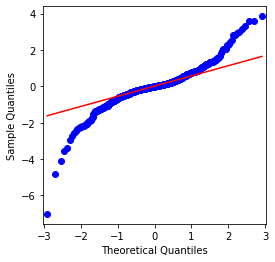
Pode-se ver que o gráfico QQ é perfeito, e a série de retorno logarítmico para Bitcoin não está em conformidade com uma distribuição normal a partir dos resultados, e tem característica óbvia de caudas grossas.

Em seguida, vamos dar uma olhada no efeito de agregação de volatilidade, ou seja, séries temporais financeiras são frequentemente acompanhadas de maior volatilidade após maior volatilidade, enquanto menor volatilidade é geralmente seguida de menor volatilidade.

O agrupamento de volatilidade reflete os efeitos de feedback positivos e negativos da volatilidade e está altamente correlacionado com as características das caudas gordas. Econometricamente, isso implica que a série temporal da volatilidade pode ser autocorrelacionada, ou seja, a volatilidade do período atual pode ter alguma relação com o período anterior, o segundo período anterior ou mesmo o terceiro período anterior.

Em [5]:

df = get_bars('huobi.btc_usdt', '1d', count=50000, start='2006-01-01')
btc_year = pd.DataFrame(df['close'],dtype=np.float)
btc_year.index.name = 'date'
btc_year.index = pd.to_datetime(btc_year.index)
btc_year['log_price'] = np.log(btc_year['close'])
btc_year['log_return'] = btc_year['log_price'] - btc_year['log_price'].shift(1)
btc_year['log_return_100x'] = np.multiply(btc_year['log_return'], 100)

btc_year_test = pd.DataFrame(btc_year['log_return'].dropna(), dtype=np.float)
btc_year_test.index.name = 'date'
sns.mpl.rcParams['figure.figsize'] = (18, 4)  # Volatility
ax1 = btc_year_test['log_return'].plot()
ax1.xaxis.label.set_visible(False)

Fora[5]:

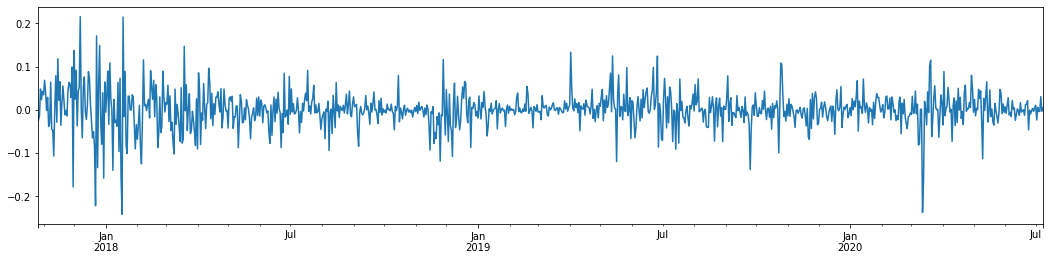
Tomando a taxa logarítmica diária de retorno do Bitcoin nos últimos 3 anos e traçando-a, o fenômeno de aglomeração de volatilidade pode ser claramente visto. Após o mercado alcista no Bitcoin em 2018, ele estava em uma posição estável na maior parte do tempo.

Em uma palavra, a partir da observação intuitiva, podemos ver que uma grande flutuação será seguida por uma flutuação densa com uma grande probabilidade, que também é o efeito de agregação da volatilidade.

1-3. Preparação de dados

Para preparar o conjunto de amostra de treinamento, primeiro, estabelecemos uma amostra de referência, na qual a taxa de retorno logarítmica é a volatilidade observada equivalente.

O método de recolha de amostras baseia-se em dados por hora, a fórmula é a seguinte: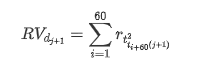

Em [4]:

count_num = 100000
start_date = '2020-03-01'

df = get_bars('huobi.btc_usdt', '1m', count=50000, start='2020-02-13')  # Take the minute data
kline_1m = pd.DataFrame(df['close'], dtype=np.float)
kline_1m.index.name = 'date'
kline_1m['log_price'] = np.log(kline_1m['close'])
kline_1m['return'] = kline_1m['close'].pct_change().dropna()
kline_1m['log_return'] = kline_1m['log_price'] - kline_1m['log_price'].shift(1)

kline_1m['squared_log_return'] = np.power(kline_1m['log_return'], 2)

kline_1m['return_100x'] = np.multiply(kline_1m['return'], 100)
kline_1m['log_return_100x'] = np.multiply(kline_1m['log_return'], 100)  # Enlarge 100 times

df = get_bars('huobi.btc_usdt', '1h', count=860, start='2020-02-13')  # Take the hour data
kline_all = pd.DataFrame(df['close'], dtype=np.float)
kline_all.index.name = 'date'
kline_all['log_price'] = np.log(kline_all['close'])  # Calculate daily logarithmic rate of return
kline_all['return'] = kline_all['log_price'].pct_change().dropna()
kline_all['log_return'] = kline_all['log_price'] - kline_all['log_price'].shift(1)  # Calculate logarithmic rate of return
kline_all['squared_log_return'] = np.power(kline_all['log_return'], 2)  # The exponential square of logarithmic daily rate of return

kline_all['return_100x'] = np.multiply(kline_all['return'], 100)
kline_all['log_return_100x'] = np.multiply(kline_all['log_return'], 100)  # Enlarge 100 times

kline_all['realized_variance_1_hour'] = kline_1m.loc[:, 'squared_log_return'].resample('h', closed='left', label='left').sum().copy()  # Resampling to days
kline_all['realized_volatility_1_hour'] = np.sqrt(kline_all['realized_variance_1_hour'])  # Volatility of variance derivation

kline_all = kline_all[4:-29] # Remove the last line because it is missing
kline_all.head(3)

Fora[4]: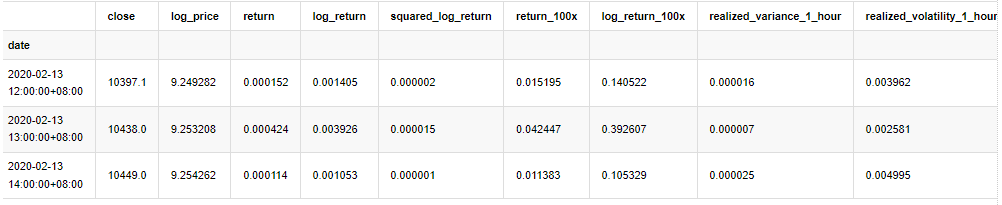

Preparar os dados fora da amostra da mesma forma

Em [5]:

# Prepare the data outside the sample with realized daily volatility
df = get_bars('huobi.btc_usdt', '1m', count=50000, start='2020-02-13')  # Take the minute data
kline_1m = pd.DataFrame(df['close'], dtype=np.float)
kline_1m.index.name = 'date'
kline_1m['log_price'] = np.log(kline_1m['close'])
kline_1m['log_return'] = kline_1m['log_price'] - kline_1m['log_price'].shift(1)
kline_1m['log_return_100x'] = np.multiply(kline_1m['log_return'], 100)  # Enlarge 100 times
kline_1m['squared_log_return'] = np.power(kline_1m['log_return_100x'], 2)
kline_1m#.tail()
df = get_bars('huobi.btc_usdt', '1h', count=860, start='2020-02-13')  # Take the hour data
kline_test = pd.DataFrame(df['close'], dtype=np.float)
kline_test.index.name = 'date'
kline_test['log_price'] = np.log(kline_test['close'])  # Calculate daily logarithmic rate of return
kline_test['log_return'] = kline_test['log_price'] - kline_test['log_price'].shift(1)  # Calculate logarithmic rate of return
kline_test['log_return_100x'] = np.multiply(kline_test['log_return'], 100)  # Enlarge 100 times
kline_test['squared_log_return'] = np.power(kline_test['log_return_100x'], 2)  # The exponential square of logarithmic daily rate of return
kline_test['realized_variance_1_hour'] = kline_1m.loc[:, 'squared_log_return'].resample('h', closed='left', label='left').sum()  # Resampling to days
kline_test['realized_volatility_1_hour'] = np.sqrt(kline_test['realized_variance_1_hour'])  # Volatility of variance derivation
kline_test = kline_test[4:-2]

A fim de compreender os dados de base da amostra, é feita uma análise descritiva simples, como se segue:

Em [9]:

line_test = pd.DataFrame(kline_train['log_return'].dropna(), dtype=np.float)
line_test.index.name = 'date'

mean = line_test.mean()  # Calculate mean value and standard deviation
std = line_test.std()

line_test.sort_values(by = 'log_return', inplace = True)  # Resort
s_r = line_test.reset_index(drop = False)  # After resorting, update index
s_r['p'] = (s_r.index - 0.5) / len(s_r)  # Calculate the percentile p(i)
s_r['q'] = (s_r['log_return'] - mean) / std  # Calculate the value of q

st = line_test.describe()
x1 ,y1 = 0.25, st['log_return']['25%']
x2 ,y2 = 0.75, st['log_return']['75%']

fig = plt.figure(figsize = (18,8))
layout = (2, 2)
ax1 = plt.subplot2grid(layout, (0, 0), colspan=2)# Plot the data distribution
ax2 = plt.subplot2grid(layout, (1, 0))# Plot histogram
ax3 = plt.subplot2grid(layout, (1, 1))# Draw the QQ chart, the straight line is the connection of the quarter digit, three-quarters digit, which is basically conforms to the normal distribution

ax1.scatter(line_test.index, line_test.values)
line_test.hist(bins=30,alpha = 0.5,ax = ax2)
line_test.plot(kind = 'kde', secondary_y=True,ax = ax2)
ax3.plot(s_r['p'],s_r['log_return'],'k.',alpha = 0.1)
ax3.plot([x1,x2],[y1,y2],'-r')
sns.despine()
plt.tight_layout()

Fora[9]:

Como resultado, há uma agregação óbvia de volatilidade e efeito de alavancagem no gráfico de séries temporais de retornos logarítmicos.

A distorção no gráfico de distribuição dos retornos logarítmicos é menor que 0, indicando que os retornos na amostra são ligeiramente negativos e tendenciosos para a direita.

A distorção da distribuição dos dados é inferior a 1, indicando que os retornos dentro da amostra são ligeiramente positivos e ligeiramente tendenciosos para a direita.

Agora que chegamos a este ponto, vamos fazer outro teste estatístico. Em [7]:

line_test = pd.DataFrame(kline_all['log_return'].dropna(), dtype=np.float)
line_test.index.name = 'date'
mean = line_test.mean()
std = line_test.std()
normal_result = pd.DataFrame(index=['Mean Value', 'Std Value', 'Skewness Value','Kurtosis Value',
                                    'Ks Test Value','Ks Test P-value',
                                    'Jarque Bera Test','Jarque Bera Test P-value'],
                    columns=['model value'])
normal_result['model value']['Mean Value'] = ('%.4f'% mean[0])
normal_result['model value']['Std Value'] = ('%.4f'% std[0])
normal_result['model value']['Skewness Value'] = ('%.4f'% line_test.skew())
normal_result['model value']['Kurtosis Value'] = ('%.4f'% line_test.kurt())
normal_result['model value']['Ks Test Value'] = stats.kstest(line_test, 'norm', (mean, std))[0]
normal_result['model value']['Ks Test P-value'] = stats.kstest(line_test, 'norm', (mean, std))[1]
normal_result['model value']['Jarque Bera Test'] = stats.jarque_bera(line_test)[0]
normal_result['model value']['Jarque Bera Test P-value'] = stats.jarque_bera(line_test)[1]
normal_result

Fora[7]:

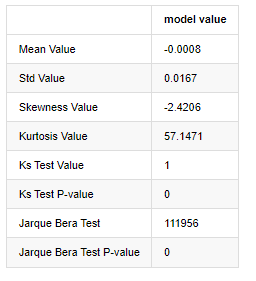
A hipótese original é caracterizada por diferença significativa e distribuição normal. Se o valor P for menor que o valor crítico de nível de confiança de 0,05%, a hipótese original é rejeitada.

Pode-se ver que o valor de curtose é maior que 3, mostrando as características de caudas de gordura espessa. Os valores de P de KS e JB são menores que o intervalo de confiança. A suposição de distribuição normal é rejeitada, o que prova que a taxa de retorno de BTC não tem as características da distribuição normal, e o estudo empírico tem as características de caudas de gordura espessa.

1-4. Comparação da volatilidade real e da volatilidade observada

Nós combinamos quadrado_log_ retorno (rendimento logarítmico ao quadrado) e variância_realizada (variância realizada) para observações.

Em [11]:

fig, ax = plt.subplots(figsize=(18, 6))
start = '2020-03-08 00:00:00+08:00'
end = '2020-03-20 00:00:00+08:00'

np.abs(kline_all['squared_log_return']).loc[start:end].plot(ax=ax,label='squared log return')
kline_all['realized_variance_1_hour'].loc[start:end].plot(ax=ax,label='realized variance')
plt.legend(loc='best')

Fora[11]:

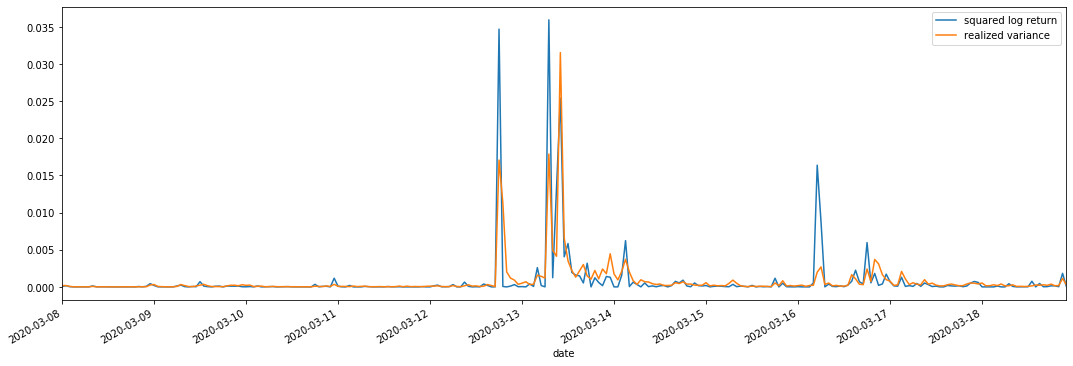
Pode-se ver que quando o intervalo de variância realizado é maior, a volatilidade do intervalo de taxa de retorno também é maior, e a taxa de retorno realizada é mais suave.

Do ponto de vista puramente teórico, a RV está mais próxima da volatilidade real, enquanto a volatilidade de curto prazo é suavizada devido à volatilidade intradiária pertence aos dados do dia a dia, portanto, do ponto de vista observacional, a volatilidade intradiária é mais adequada para uma menor frequência de volatilidade do mercado de ações.

2. Suavidade das séries temporais

Se for uma série não estacionária, ela precisa ser ajustada aproximadamente a uma série estacionária. A maneira comum é fazer processamento de diferença. Teoricamente, após muitas vezes de diferença, a série não estacionária pode ser aproximada a uma série estacionária. Se a covariância da série de amostra for estável, a expectativa, a variância e a covariância de suas observações não mudarão com o tempo, indicando que a série de amostra é mais conveniente para inferência na análise estatística.

O teste de raiz de unidade, ou seja, o teste ADF, é usado aqui. O teste ADF usa o teste t para observar a significância. Em princípio, se a série não mostrar tendência óbvia, apenas itens constantes são mantidos. Se a série tiver tendência, a equação de regressão deve incluir itens constantes e itens de tendência de tempo. Além disso, os critérios AIC e BIC podem ser usados para avaliação com base em critérios de informação.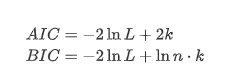

Em [8]:

stable_test = kline_all['log_return']
adftest = sm.tsa.stattools.adfuller(np.array(stable_test), autolag='AIC')
adftest2 = sm.tsa.stattools.adfuller(np.array(stable_test), autolag='BIC')
output=pd.DataFrame(index=['ADF Statistic Test Value', "ADF P-value", "Lags", "Number of Observations",
                           "Critical Value(1%)","Critical Value(5%)","Critical Value(10%)"],
                    columns=['AIC','BIC'])
output['AIC']['ADF Statistic Test Value'] = adftest[0]
output['AIC']['ADF P-value'] = adftest[1]
output['AIC']['Lags'] = adftest[2]
output['AIC']['Number of Observations'] = adftest[3]
output['AIC']['Critical Value(1%)'] = adftest[4]['1%']
output['AIC']['Critical Value(5%)'] = adftest[4]['5%']
output['AIC']['Critical Value(10%)'] = adftest[4]['10%']
output['BIC']['ADF Statistic Test Value'] = adftest2[0]
output['BIC']['ADF P-value'] = adftest2[1]
output['BIC']['Lags'] = adftest2[2]
output['BIC']['Number of Observations'] = adftest2[3]
output['BIC']['Critical Value(1%)'] = adftest2[4]['1%']
output['BIC']['Critical Value(5%)'] = adftest2[4]['5%']
output['BIC']['Critical Value(10%)'] = adftest2[4]['10%']
output

Fora[8]: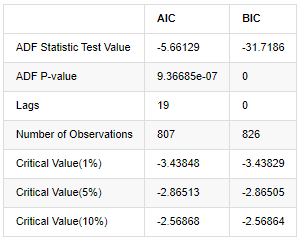

A suposição original é que não há raiz de unidade na série, ou seja, a suposição alternativa é que a série é estacionária.

3. Identificação do modelo e determinação da ordem

Para estabelecer a equação do valor médio, é necessário fazer um teste de autocorrelação na sequência para garantir que o termo de erro não tenha autocorrelação.

Em [19]:

tsplot(kline_all['log_return'], kline_all['log_return'], title='Log Return', lags=100)

Fora [1]:

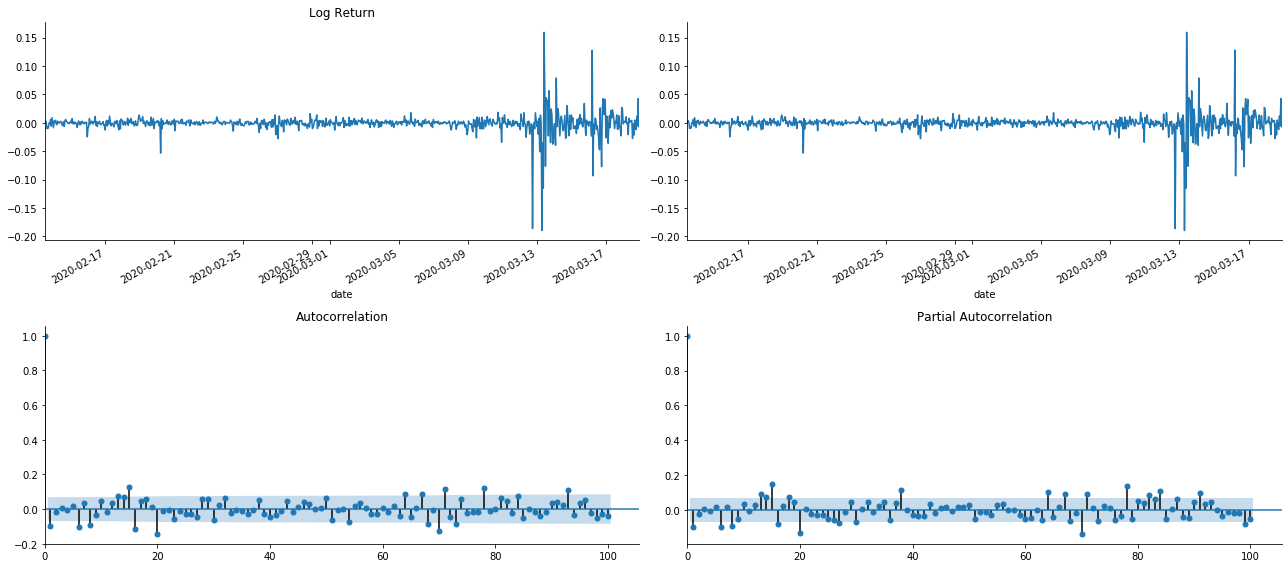
Como podemos ver, o efeito de truncamento é perfeito. Nesse momento, esta imagem me deu uma inspiração. O mercado é realmente inválido? Para verificar, faremos análise de autocorrelação na série de retorno e determinaremos a ordem de atraso do modelo.

O coeficiente de correlação comumente usado é para medir a correlação entre ele e si mesmo, ou seja, a correlação entre r(t) e r (t-l) em um determinado momento no passado: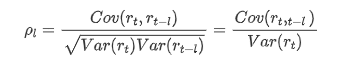

Em seguida, vamos fazer um teste quantitativo. A suposição original é que todos os coeficientes de autocorrelação são 0, ou seja, não há autocorrelação na série.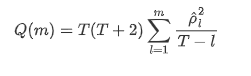

Foram tomados dez coeficientes de autocorrelação para análise, do seguinte modo:

Em [9]:

acf,q,p = sm.tsa.acf(kline_all['log_return'], nlags=15,unbiased=True,qstat = True, fft=False)  # Test 10 autocorrelation coefficients
output = pd.DataFrame(np.c_[range(1,16), acf[1:], q, p], columns=['lag', 'ACF', 'Q', 'P-value'])
output = output.set_index('lag')
output

Fora[9]: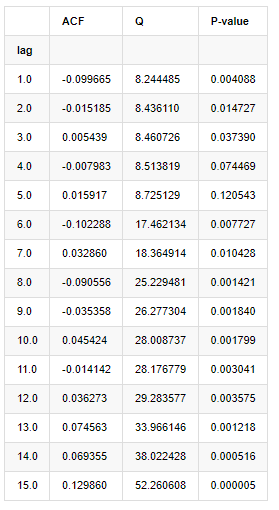

De acordo com a estatística de teste Q e o valor P, podemos ver que a função de autocorrelação ACF gradualmente se torna 0 após a ordem 0. Os valores P das estatísticas de teste Q são pequenos o suficiente para rejeitar a suposição original, então há autocorrelação na série.

4. Modelagem ARMA

Os modelos AR e MA são bastante simples. Para simplificar, Markdown está cansado demais para escrever fórmulas. Se você estiver interessado, por favor, verifique-os você mesmo. O modelo AR (Autoregressão) é usado principalmente para modelar séries de tempo. Se a série passou no teste ACF, ou seja, o coeficiente de autocorrelação com um intervalo de 1 é significativo, ou seja, os dados no tempo podem ser úteis para prever o tempo t.

O modelo MA (média móvel) usa a interferência aleatória ou a previsão de erro dos períodos q passados para expressar o valor de previsão atual linearmente.

Para descrever completamente a estrutura dinâmica dos dados, é necessário aumentar a ordem dos modelos AR ou MA, mas tais parâmetros tornarão o cálculo mais complexo.

Uma vez que as séries temporais de preços são geralmente não estacionárias, e o efeito de otimização do método de diferença sobre a estacionalidade foi discutido anteriormente, o modelo ARIMA (p, d, q) (média móvel autorregressiva de soma) adiciona processamento de diferença de ordem d com base na aplicação de modelos existentes para séries.

Em uma palavra, a única diferença entre o modelo ARIMA e o processo de construção do modelo ARMA é que, se os resultados instáveis forem obtidos após analisar a estabilidade, o modelo fará uma diferença quadrática para a série diretamente e, em seguida, executará o teste de estabilidade, e, em seguida, determinará a ordem p e q até que a série seja estável.

4-1. Selecção da ordem

Em seguida, podemos selecionar a ordem diretamente pelo critério de informação, aqui tentamos com os diagramas termodinâmicos de AIC e BIC.

Em [10]:

def select_best_params():
    ps = range(0, 4)
    ds= range(1, 2)
    qs = range(0, 4)
    parameters = product(ps, ds, qs)
    parameters_list = list(parameters)

    p_min = 0
    d_min = 0
    q_min = 0
    p_max = 3
    d_max = 3
    q_max = 3

    results_aic = pd.DataFrame(index=['AR{}'.format(i) for i in range(p_min,p_max+1)],
                               columns=['MA{}'.format(i) for i in range(q_min,q_max+1)])
    results_bic = pd.DataFrame(index=['AR{}'.format(i) for i in range(p_min,p_max+1)],
                               columns=['MA{}'.format(i) for i in range(q_min,q_max+1)])
    
    best_params = []
    aic_results = []
    bic_results = []
    hqic_results = []
    best_aic = float("inf")
    best_bic = float("inf")
    best_hqic = float("inf")
    warnings.filterwarnings('ignore')
    for param in parameters_list:
        try:
            model = sm.tsa.SARIMAX(kline_all['log_price'], order=(param[0], param[1], param[2])).fit(disp=-1)
            results_aic.loc['AR{}'.format(param[0]), 'MA{}'.format(param[2])] = model.aic
            results_bic.loc['AR{}'.format(param[0]), 'MA{}'.format(param[2])] = model.bic
        except ValueError:
            continue    
           
        aic_results.append([param, model.aic])
        bic_results.append([param, model.bic])
        hqic_results.append([param, model.hqic])
    
    results_aic = results_aic[results_aic.columns].astype(float)
    results_bic = results_bic[results_bic.columns].astype(float)
    
    # Draw thermodynamic diagrams of AIC and BIC to find the best
    fig = plt.figure(figsize=(18, 9))
    layout = (2, 2)
    aic_ax = plt.subplot2grid(layout, (0, 0))
    bic_ax = plt.subplot2grid(layout, (0, 1))

    aic_ax = sns.heatmap(results_aic,mask=results_aic.isnull(),ax=aic_ax,cmap='OrRd',annot=True,fmt='.2f',);
    aic_ax.set_title('AIC');
    bic_ax = sns.heatmap(results_bic,mask=results_bic.isnull(),ax=bic_ax,cmap='OrRd',annot=True,fmt='.2f',);
    bic_ax.set_title('BIC');
    
    aic_df = pd.DataFrame(aic_results)
    aic_df.columns = ['params', 'aic']   
    best_params.append(aic_df.params[aic_df.aic.idxmin()])
    print('AIC best param: {}'.format(aic_df.params[aic_df.aic.idxmin()]))
    
    bic_df = pd.DataFrame(bic_results)
    bic_df.columns = ['params', 'bic']
    best_params.append(bic_df.params[bic_df.bic.idxmin()])
    print('BIC best param: {}'.format(bic_df.params[bic_df.bic.idxmin()]))
    
    hqic_df = pd.DataFrame(hqic_results)
    hqic_df.columns = ['params', 'hqic']
    best_params.append(hqic_df.params[hqic_df.hqic.idxmin()])
    print('HQIC best param: {}'.format(hqic_df.params[hqic_df.hqic.idxmin()]))

    for best_param in best_params:
        if best_params.count(best_param)>=2:
            print('Best Param Selected: {}'.format(best_param))
            return best_param 

best_param = select_best_params()

Fora[10]: Melhor parâmetro AIC: (0, 1, 1) Melhor parâmetro BIC: (0, 1, 1) Melhor parâmetro HQIC: (0, 1, 1) Melhor Param selecionado: (0, 1, 1)

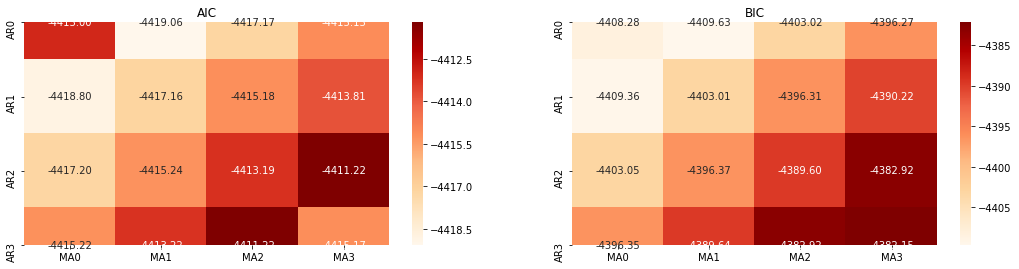
É óbvio que a combinação de parâmetros de primeira ordem ideal para o preço logarítmico é (0,1,1), o que é simples e direto. O log_return (taxa logarítmica de retorno) executa a mesma operação. O valor ideal do AIC é (4,3), e o valor ideal do BIC é (0,1).

4-2 Modelagem e correspondência ARMA

Não são necessários coeficientes trimestrais, mas SARIMAX é mais rico em atributos, por isso foi decidido escolher este modelo para modelagem e, incidentalmente, fazer uma análise descritiva da seguinte forma:

Em [11]:

params = (0, 0, 1)
training_model = smt.SARIMAX(endog=kline_all['log_return'], trend='c', order=params, seasonal_order=(0, 0, 0, 0))
model_results = training_model.fit(disp=False)
model_results.summary()

Fora[11]: Resultados do Modelo do Espaço Estadual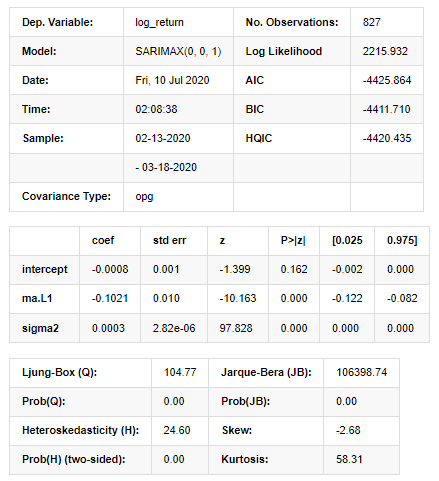

Aviso: [1] Matriz de covariância calculada usando o produto externo dos gradientes (passo complexo). Em [27]:

model_results.plot_diagnostics(figsize=(18, 10));

Fora[27]:

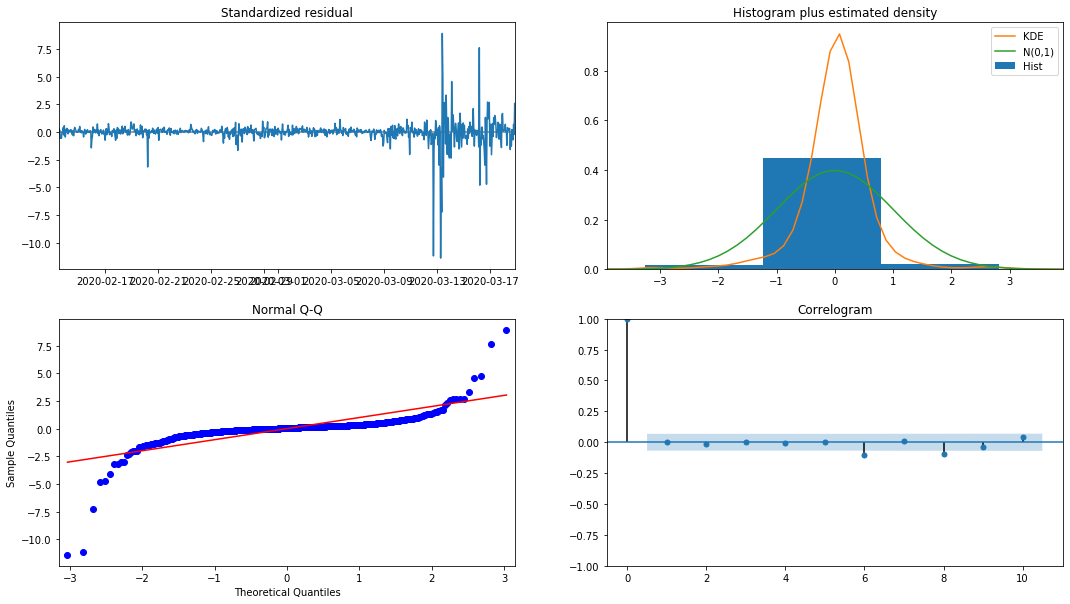
A densidade de probabilidade KDE no histograma está longe da distribuição normal N (0,1), indicando que o residual não é uma distribuição normal.

Em seguida, tendo dito isso, se o modelo pode ser usado ainda precisa ser testado.

4-3. Teste do modelo

O efeito de correspondência do residual não é ideal, então realizamos o teste de Durbin Watson sobre ele. A hipótese original do teste é que a sequência não tem autocorrelação, e a sequência de hipótese alternativa é estacionária. Além disso, se os valores de P dos testes LB, JB e H forem menores que o valor crítico de nível de confiança de 0,05%, a hipótese original será rejeitada.

Em [12]:

het_method='breakvar'
norm_method='jarquebera'
sercor_method='ljungbox'

(het_stat, het_p) = model_results.test_heteroskedasticity(het_method)[0]
norm_stat, norm_p, skew, kurtosis = model_results.test_normality(norm_method)[0]

sercor_stat, sercor_p = model_results.test_serial_correlation(method=sercor_method)[0]
sercor_stat = sercor_stat[-1] # The last value of the maximum period
sercor_p = sercor_p[-1]

dw = sm.stats.stattools.durbin_watson(model_results.filter_results.standardized_forecasts_error[0, model_results.loglikelihood_burn:])

arroots_outside_unit_circle = np.all(np.abs(model_results.arroots) > 1)
maroots_outside_unit_circle = np.all(np.abs(model_results.maroots) > 1)

print('Test heteroskedasticity of residuals ({}): stat={:.3f}, p={:.3f}'.format(het_method, het_stat, het_p));
print('\nTest normality of residuals ({}): stat={:.3f}, p={:.3f}'.format(norm_method, norm_stat, norm_p));
print('\nTest serial correlation of residuals ({}): stat={:.3f}, p={:.3f}'.format(sercor_method, sercor_stat, sercor_p));
print('\nDurbin-Watson test on residuals: d={:.2f}\n\t(NB: 2 means no serial correlation, 0=pos, 4=neg)'.format(dw))
print('\nTest for all AR roots outside unit circle (>1): {}'.format(arroots_outside_unit_circle))
print('\nTest for all MA roots outside unit circle (>1): {}'.format(maroots_outside_unit_circle))

root_test=pd.DataFrame(index=['Durbin-Watson test on residuals','Test for all AR roots outside unit circle (>1)','Test for all MA roots outside unit circle (>1)'],columns=['c'])
root_test['c']['Durbin-Watson test on residuals']=dw
root_test['c']['Test for all AR roots outside unit circle (>1)']=arroots_outside_unit_circle
root_test['c']['Test for all MA roots outside unit circle (>1)']=maroots_outside_unit_circle
root_test

Fora[12]: Heteroskedasticidade dos resíduos de ensaio (breakvar): stat=24.598, p=0.000

Normalidade do ensaio de resíduos (jarquebera): stat=106398.739, p=0.000

Correlação dos resíduos em série de ensaio (caixa de leitura): stat=104.767, p=0.000

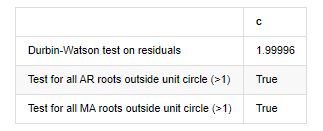
Teste de Durbin-Watson para resíduos: d=2,00 (NB: 2 significa que não há correlação serial, 0=pos, 4=negativo)

Teste para todas as raízes AR fora do círculo unitário (>1): verdadeiro

Teste para todas as raízes MA fora do círculo unitário (>1): verdadeiro

Em [13]:

kline_all['log_price_dif1'] = kline_all['log_price'].diff(1)
kline_all = kline_all[1:]
kline_train = kline_all

training_label = 'log_return'
training_ts = pd.DataFrame(kline_train[training_label], dtype=np.float)

delta = model_results.fittedvalues - training_ts[training_label]
adjR = 1 - delta.var()/training_ts[training_label].var()
adjR_test=pd.DataFrame(index=['adjR2'],columns=['Value'])
adjR_test['Value']['adjR2']=adjR**2
adjR_test

Fora[13]:

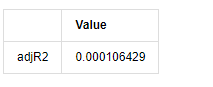
Se a estatística do teste de Durbin Watson for igual a 2, confirma que a série não tem correlação, e seu valor estatístico é distribuído entre (0,4). Próximo de 0 significa que a correlação positiva é alta, enquanto perto de 4 significa que a correlação negativa é alta. Aqui é aproximadamente igual a 2. O valor P de outros testes é pequeno o suficiente, a raiz característica da unidade está fora do círculo unitário, e quanto maior o valor do adjR2 modificado, melhor será. O resultado geral da medida não parece ser satisfatório.

Em [14]:

model_results.params

Fora [1]: Interceptação -0.000817 Ma.L1 -0.102102 sigma2 0,000275 dtipo: float64

Para resumir, este parâmetro de configuração de ordem pode basicamente atender aos requisitos de modelagem de séries temporais e modelagem de volatilidade subsequente, mas o efeito de correspondência é o seguinte.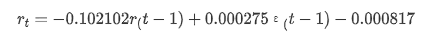

4-4. Previsão do modelo

Em seguida, o modelo treinado é correspondido para a frente. os modelos de estatísticas fornecem opções estáticas e dinâmicas para correspondência e previsão. A diferença está em se o valor de observação é usado na próxima etapa da previsão, ou o valor de previsão gerado na etapa anterior é usado iterativamente. Os efeitos de previsão do log_return (taxa logarítmica de retorno) são os seguintes:

Em [37]:

start_date = '2020-02-28 12:00:00+08:00'
end_date = start_date 

pred_dy = model_results.get_prediction(start=start_date, dynamic=False)
pred_dy_ci = pred_dy.conf_int()

fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(18, 6))
ax.plot(kline_all['log_return'].loc[start_date:], label='Log Return', linestyle='-')
ax.plot(pred_dy.predicted_mean.loc[start_date:], label='Forecast Log Return', linestyle='--')
ax.fill_between(pred_dy_ci.index,pred_dy_ci.iloc[:, 0],pred_dy_ci.iloc[:, 1], color='g', alpha=.25)

plt.ylabel("BTC Log Return")
plt.legend(loc='best')
plt.tight_layout()
sns.despine()

Fora[37]:

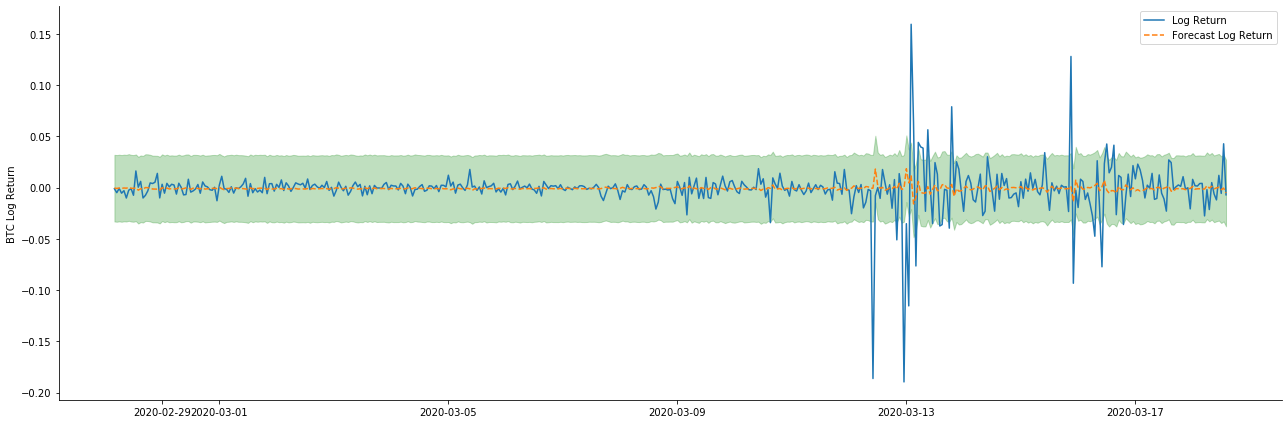
Pode-se ver que o efeito de ajuste do modo estático na amostra é excelente, os dados da amostra podem ser quase cobertos por um intervalo de confiança de 95% e o modo dinâmico está um pouco fora de controle.

Então vamos olhar para o efeito de correspondência de dados no modo dinâmico:

Em [38]:

start_date = '2020-02-28 12:00:00+08:00'
end_date = start_date 

pred_dy = model_results.get_prediction(start=start_date, dynamic=True)
pred_dy_ci = pred_dy.conf_int()

fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(18, 6))
ax.plot(kline_all['log_return'].loc[start_date:], label='Log Return', linestyle='-')
ax.plot(pred_dy.predicted_mean.loc[start_date:], label='Forecast Log Return', linestyle='--')
ax.fill_between(pred_dy_ci.index,pred_dy_ci.iloc[:, 0],pred_dy_ci.iloc[:, 1], color='g', alpha=.25)

plt.ylabel("BTC Log Return")
plt.legend(loc='best')
plt.tight_layout()
sns.despine()

Fora[38]:

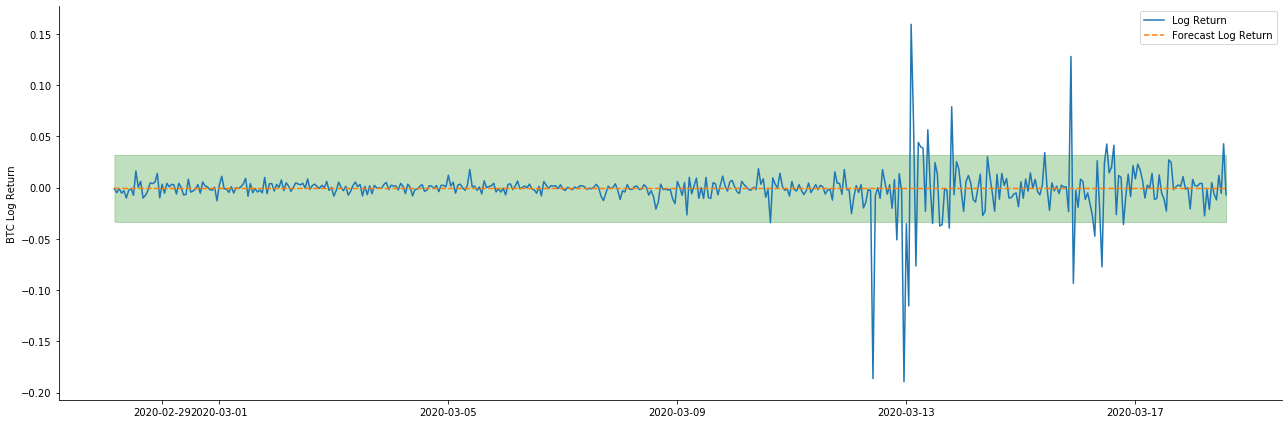
Pode-se ver que o efeito de ajuste dos dois modelos na amostra é excelente, e o valor médio pode ser quase coberto pelo intervalo de confiança de 95%, mas o modelo estático é obviamente mais adequado.

Em [41]:

# Out-of-sample predicted data predict()
start_date = '2020-03-01 12:00:00+08:00'
end_date = '2020-03-20 23:00:00+08:00'
model = False

predict_step = 50
predicts_ARIMA_normal = model_results.get_prediction(start=start_date, dynamic=model, full_reports=True)
ci_normal = predicts_ARIMA_normal.conf_int().loc[start_date:]

predicts_ARIMA_normal_out = model_results.get_forecast(steps=predict_step, dynamic=model)
ci_normal_out = predicts_ARIMA_normal_out.conf_int().loc[start_date:end_date]

fig, ax = plt.subplots(figsize=(18,8))
kline_test.loc[start_date:end_date, 'log_return'].plot(ax=ax, label='Benchmark Log Return')

predicts_ARIMA_normal.predicted_mean.plot(ax=ax, style='g', label='In Sample Forecast')
ax.fill_between(ci_normal.index, ci_normal.iloc[:,0], ci_normal.iloc[:,1], color='g', alpha=0.1)

predicts_ARIMA_normal_out.predicted_mean.loc[:end_date].plot(ax=ax, style='r--', label='Out of Sample Forecast')
ax.fill_between(ci_normal_out.index, ci_normal_out.iloc[:,0], ci_normal_out.iloc[:,1], color='r', alpha=0.1)

plt.tight_layout()
plt.legend(loc='best')
sns.despine()

Fora[41]:

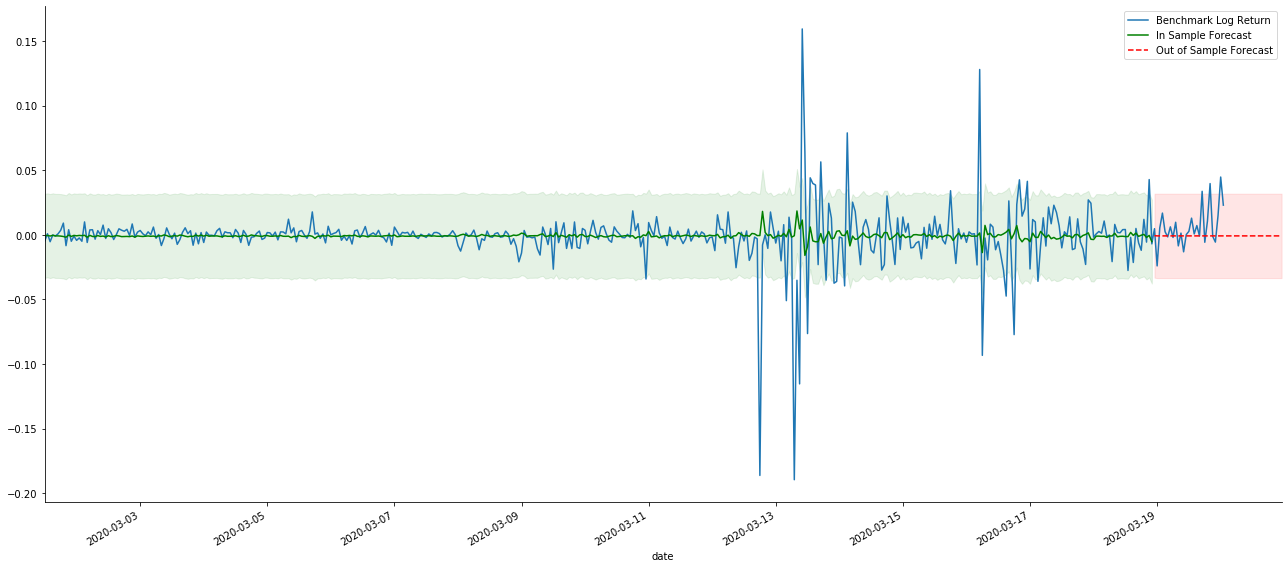
Como a correspondência de dados na amostra é uma previsão avançada, quando a quantidade de informações na amostra é suficiente, o modelo estático é propenso a uma correspondência excessiva, enquanto o modelo dinâmico carece de variáveis dependentes confiáveis, e o efeito torna-se cada vez pior após a iteração.

Se invertermos a previsão da taxa de retorno para log_price (preço logarítmico), a correspondência é mostrada na figura abaixo:

Em [42]:

params = (0, 1, 1)
mod = smt.SARIMAX(endog=kline_all['log_price'], trend='c', order=params, seasonal_order=(0, 0, 0, 0))
res = mod.fit(disp=False)

start_date = '2020-03-01 12:00:00+08:00'
end_date = '2020-03-15 23:00:00+08:00'

predicts_ARIMA_normal = res.get_prediction(start=start_date, dynamic=False, full_results=False)
predicts_ARIMA_dynamic = res.get_prediction(start=start_date, dynamic=True, full_results=False)

fig, ax = plt.subplots(figsize=(18,6))
kline_test.loc[start_date:end_date, 'log_price'].plot(ax=ax, label='Log Price')

predicts_ARIMA_normal.predicted_mean.loc[start_date:end_date].plot(ax=ax, style='r--', label='Normal Prediction')
ci_normal = predicts_ARIMA_normal.conf_int().loc[start_date:end_date]
ax.fill_between(ci_normal.index, ci_normal.iloc[:,0], ci_normal.iloc[:,1], color='r', alpha=0.1)

predicts_ARIMA_dynamic.predicted_mean.loc[start_date:end_date].plot(ax=ax, style='g', label='Dynamic Prediction')
ci_dynamic = predicts_ARIMA_dynamic.conf_int().loc[start_date:end_date]
ax.fill_between(ci_dynamic.index, ci_dynamic.iloc[:,0], ci_dynamic.iloc[:,1], color='g', alpha=0.1)

plt.tight_layout()
plt.legend(loc='best')
sns.despine()

Fora[42]:

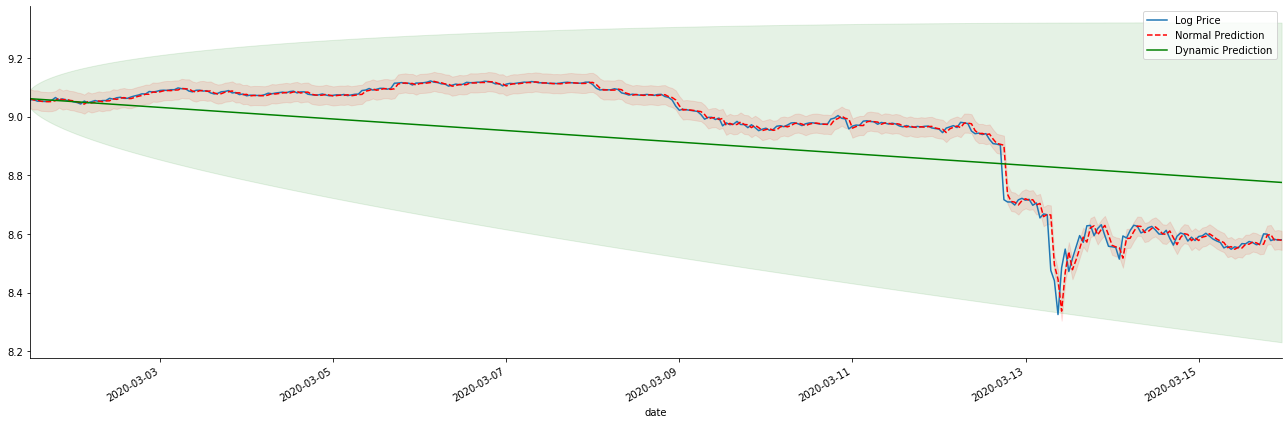
É fácil ver as vantagens de correspondência do modelo estático e a extrema diferença entre o modelo dinâmico e o modelo estático na previsão de longo prazo. A linha pontilhada vermelha e o intervalo rosa... Você não pode dizer que a previsão deste modelo é errada. Afinal, ele cobre a tendência da média móvel completamente, mas... é significativo?

Na verdade, o modelo ARMA em si não está errado, porque o problema não é o modelo em si, mas a lógica objetiva das coisas em si. O modelo de série temporal só pode ser estabelecido com base na correlação entre observações anteriores e subsequentes. Portanto, é impossível modelar a série de ruído branco. Portanto, todo o trabalho anterior é baseado em uma suposição ousada de que a série de taxa de retorno do BTC não pode ser independente e distribuída de forma idêntica.

Em geral, as séries de taxa de retorno são séries de diferença de martingale, o que significa que a taxa de retorno é imprevisível e a suposição de fraca eficiência do mercado correspondente se mantém.

No entanto, a sequência residual combinada também é uma sequência de diferença de martingale. A sequência de diferença de martingale pode não ser independente e distribuída de forma idêntica, mas a variância condicional pode depender do valor passado, então a autocorrelação de primeira ordem desapareceu, mas ainda há autocorrelação de ordem superior, que também é um pré-requisito importante para a volatilidade ser modelada e observada.

Se tal lógica for válida, então a premissa de construir vários modelos de volatilidade também é válida. Então, para uma série de taxa de retorno, se um mercado fraco eficiente for satisfeito, então o valor médio deve ser difícil de prever, mas a variância é previsível.

Por último, vamos avaliar o efeito da previsão de forma simples.

Em [15]:

start = '2020-02-14 00:00:00+08:00'
predicts_ARIMA_normal = model_results.get_prediction(dynamic=False)
predicts_ARIMA_dynamic = model_results.get_prediction(dynamic=True)
training_label = 'log_return'

compare_ARCH_X = pd.DataFrame()
compare_ARCH_X['Model'] = ['NORMAL','DYNAMIC']
compare_ARCH_X['RMSE'] = [rmse(predicts_ARIMA_normal.predicted_mean[1:], kline_test[training_label][:826]),
                          rmse(predicts_ARIMA_dynamic.predicted_mean[1:], kline_test[training_label][:826])]
compare_ARCH_X['MAPE'] = [mape(predicts_ARIMA_normal.predicted_mean[:50], kline_test[training_label][:50]),
                          mape(predicts_ARIMA_dynamic.predicted_mean[:50], kline_test[training_label][:50])]
compare_ARCH_X

Fora [1]: Erro médio quadrado da raiz (RMSE): 0,0184 Erro médio quadrado da raiz (RMSE): 0,0167 Erro médio em percentagem absoluta (MAPE): 2,25e+03 Percentagem média de erro absoluto (MAPE): 395

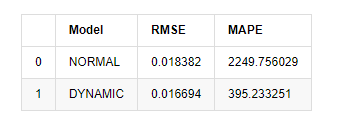
Pode-se ver que o modelo estático é ligeiramente melhor do que o modelo dinâmico em termos da coincidência de erro entre o valor previsto e o valor real. Ele corresponde bem à taxa de retorno logarítmico do Bitcoin, que é basicamente alinhada com as expectativas. A previsão dinâmica carece de informações variáveis mais precisas, e o erro também é ampliado pela iteração, de modo que o efeito de previsão é pobre. O MAPE é maior que 100%, de modo que a qualidade de correspondência real de ambos os modelos não é ideal.

Em [18]:

predict_step = 50
predicts_ARIMA_normal_out = model_results.get_forecast(steps=predict_step, dynamic=False)
predicts_ARIMA_dynamic_out = model_results.get_forecast(steps=predict_step, dynamic=True)
testing_ts = kline_test
training_label = 'log_return'

compare_ARCH_X = pd.DataFrame()
compare_ARCH_X['Model'] = ['NORMAL','DYNAMIC']
compare_ARCH_X['RMSE'] = [get_rmse(predicts_ARIMA_normal_out.predicted_mean, testing_ts[training_label]),
                          get_rmse(predicts_ARIMA_dynamic_out.predicted_mean, testing_ts[training_label])]
compare_ARCH_X['MAPE'] = [get_mape(predicts_ARIMA_normal_out.predicted_mean, testing_ts[training_label]),
                          get_mape(predicts_ARIMA_dynamic_out.predicted_mean, testing_ts[training_label])]
compare_ARCH_X

Fora [1]:

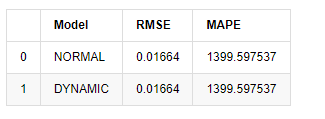
Uma vez que a próxima previsão fora da amostra depende dos resultados da etapa anterior, apenas o modelo dinâmico é eficaz. No entanto, o defeito de erro de longo prazo do modelo dinâmico leva à capacidade de previsão insuficiente do modelo geral, de modo que o próximo passo é previsto no máximo.

Para resumir, o modelo estático do modelo ARMA é adequado para combinar a taxa de retorno intra amostra do Bitcoin. A previsão de curto prazo da taxa de retorno pode cobrir o intervalo de confiança efetivamente, mas a previsão de longo prazo é muito difícil, o que atende à fraca eficácia do mercado. Após o teste, a taxa de retorno dentro do intervalo de amostra atende à premissa de observação de volatilidade subsequente.

5. Efeito ARCH

O efeito do modelo ARCH é a correlação de série da seqüência de heteroscedasticidade condicional. O teste de mistura Ljung Box é usado para testar a correlação da série quadrada residual para determinar se há efeito ARCH. Se o teste do efeito ARCH for aprovado, ou seja, a série tem heteroscedasticidade, o próximo passo da modelagem GARCH pode ser realizado para estimar a equação média e a equação de volatilidade em conjunto. Caso contrário, o modelo precisa ser otimizado e reajustado, como processamento diferencial ou série recíproca.

Preparamos aqui alguns conjuntos de dados e variáveis globais:

Em [33]:

count_num = 100000
start_date = '2020-03-01'

df = get_bars('huobi.btc_usdt', '1m', count=count_num, start=start_date)  # Take the minute data
kline_1m = pd.DataFrame(df['close'], dtype=np.float)
kline_1m.index.name = 'date'
kline_1m['log_price'] = np.log(kline_1m['close'])
kline_1m['return'] = kline_1m['close'].pct_change().dropna()
kline_1m['log_return'] = kline_1m['log_price'] - kline_1m['log_price'].shift(1)

kline_1m['squared_log_return'] = np.power(kline_1m['log_return'], 2)

kline_1m['return_100x'] = np.multiply(kline_1m['return'], 100)
kline_1m['log_return_100x'] = np.multiply(kline_1m['log_return'], 100)  # Enlarge 100 times

df = get_bars('huobi.btc_usdt', '1h', count=count_num, start=start_date)  # Take the hour data
kline_test = pd.DataFrame(df['close'], dtype=np.float)
kline_test.index.name = 'date'
kline_test['log_price'] = np.log(kline_test['close'])  # Calculate the daily logarithmic rate of return
kline_test['return'] = kline_test['log_price'].pct_change().dropna()
kline_test['log_return'] = kline_test['log_price'] - kline_test['log_price'].shift(1)  # Calculate the logarithmic rate of return
kline_test['squared_log_return'] = np.power(kline_test['log_return'], 2)  # Exponential square of log daily return rate

kline_test['return_100x'] = np.multiply(kline_test['return'], 100)
kline_test['log_return_100x'] = np.multiply(kline_test['log_return'], 100)  # Enlarge 100 times

kline_test['realized_variance_1_hour'] = kline_1m.loc[:, 'squared_log_return'].resample('h', closed='left', label='left').sum().copy() # Resampling to days 
kline_test['realized_volatility_1_hour'] = np.sqrt(kline_test['realized_variance_1_hour'])  # Volatility of variance derivation

kline_test = kline_test[4:-2500]
kline_test.head(3)

Fora[33]:

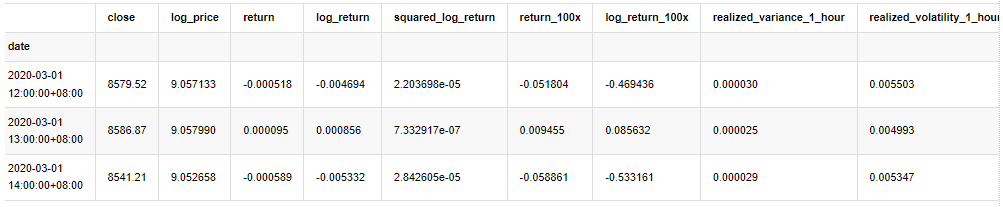
Em [22]:

cc = 3
model_p = 1
predict_lag = 30
label = 'log_return'

training_label = label
training_ts = pd.DataFrame(kline_test[training_label], dtype=np.float)

training_arch_label = label
training_arch = pd.DataFrame(kline_test[training_arch_label], dtype=np.float)

training_garch_label = label
training_garch = pd.DataFrame(kline_test[training_garch_label], dtype=np.float)

training_egarch_label = label
training_egarch = pd.DataFrame(kline_test[training_egarch_label], dtype=np.float)

training_arch.plot(figsize = (18,4))

Fora[22]: O que é que se passa?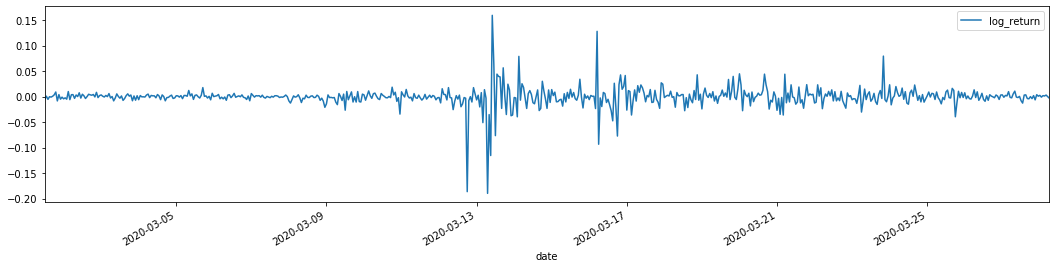

As taxas de retorno logarítmicas são mostradas acima. Em seguida, precisamos testar o efeito ARCH da amostra. Nós estabelecemos a série residual dentro da amostra com base no ARMA. Algumas séries e a série quadrada de residual e residual são calculadas primeiro:

Em [20]:

training_arma_model = smt.SARIMAX(endog=training_ts, trend='c', order=(0, 0, 1), seasonal_order=(0, 0, 0, 0))
arma_model_results = training_arma_model.fit(disp=False)
arma_model_results.summary()
training_arma_fitvalue = pd.DataFrame(arma_model_results.fittedvalues,dtype=np.float)
at = pd.merge(training_ts, training_arma_fitvalue, on='date')
at.columns = ['log_return', 'model_fit']
at['res'] = at['log_return'] - at['model_fit']
at['res2'] = np.square(at['res'])
at.head()

Fora [1]:

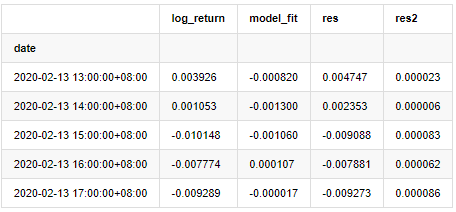
A série residual da amostra é então traçada

Em [69]:

fig, ax = plt.subplots(figsize=(18, 6))
ax1 = fig.add_subplot(2,1,1)
at['res'][1:].plot(ax=ax1,label='resid')
plt.legend(loc='best')

ax2 = fig.add_subplot(2,1,2)
at['res2'][1:].plot(ax=ax2,label='resid2')

plt.legend(loc='best')
plt.tight_layout()
sns.despine()

Fora[69]:

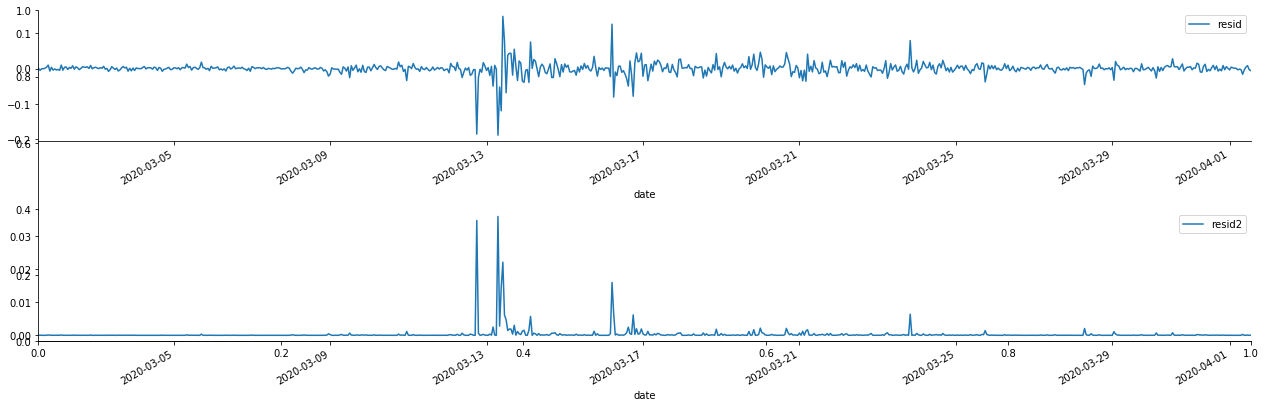
Pode-se ver que a série residual tem características de agregação óbvias, e pode-se julgar inicialmente que a série tem efeito ARCH.

Em [70]:

figure = plt.figure(figsize=(18,4))
ax1 = figure.add_subplot(111)
fig = sm.graphics.tsa.plot_acf(at['res2'],lags = 40, ax=ax1)

Fora[70]:

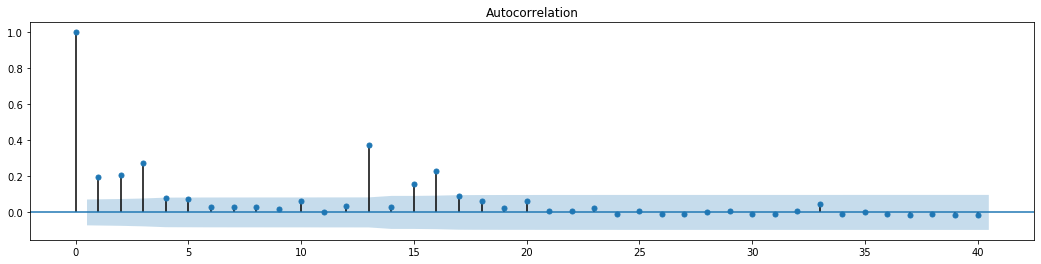
A suposição original para o teste de mistura de séries é que a série não tem correlação. Pode-se ver que os valores P correspondentes das primeiras 20 ordens de dados são menores que o valor crítico do nível de confiança de 0,05%. Portanto, a suposição original é rejeitada, ou seja, o residual da série tem o efeito ARCH. O modelo de variância pode ser estabelecido através do modelo de tipo ARCH para se adequar à heteroscedasticidade da série residual e prever ainda mais a volatilidade.

6. Modelagem GARCH

Antes de executar a modelagem GARCH, precisamos lidar com a parte de cauda gorda da série. Porque o termo de erro da série na hipótese precisa estar em conformidade com a distribuição normal ou distribuição t, e verificamos anteriormente que a série de rendimento tem uma distribuição de cauda gorda, então precisamos descrever e complementar essa parte.

Na modelagem GARCH, o item de erro fornece as opções de distribuição normal, distribuição t, distribuição GED (distribuição de erro generalizada) e distribuição t dos estudantes esquivados.

Relacionados

Mais.