KNN الگورتھم پر مبنی Bayesian درجہ بندی

درجہ بندی کے فیصلے کرنے کے لئے درجہ بندی کے ڈیزائن کے لئے نظریاتی بنیاد بیزس فیصلہ سازی کی تھیوری:

موازنہ P(ωi 173x) ◄ جہاںωi کلاس i ہے اور x ایک ایسا ڈیٹا ہے جس کا مشاہدہ کیا گیا ہے اور اسے درجہ بندی کرنا ہے۔ P(ωi 173x) اس اعداد و شمار کی خصوصیت والے ویکٹر کی صورت میں اس کا فیصلہ کرنے کا امکان کیا ہے کہ یہ کلاس i سے تعلق رکھتا ہے۔ یہ بھی بعد از امتحان کا امکان ہے۔ بیس فارمولے کے مطابق ، اس کی نمائندگی کی جاسکتی ہے:

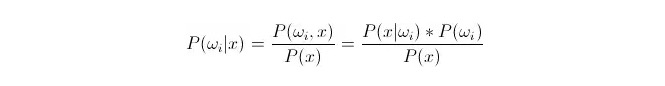
ان میں سے ، P ((xfin_Latnfin_Latnfin_Latnfin_Latnfin_Latnfin_Latn) i) on samankaltaisuusprobability یا conditional probability; P ((ωi) is called antecedent probability, because it is irrelevant to the experiment and can be known before the experiment.

درجہ بندی کرتے وقت ، دیئے گئے x ، اس زمرے کا انتخاب کریں جس سے بعد میں جانچ پڑتال کا امکان P ((ωi 173x) سب سے زیادہ ہو۔ ہر زمرے کے تحت P ((ωi 173x) کا موازنہ کرتے وقت ،ωi متغیر ہے ، اور x مقررہ ہے۔ لہذا P (((x) کو خارج کردیا جاسکتا ہے ، اس پر غور نہیں کیا جاسکتا۔

تو اس کا خلاصہ یہ ہے کہ P{\displaystyle P{\displaystyle x}*P ((ωi) سوال پیشگی امکان P ((ωi) ، صرف اعداد و شمار کی تربیت پر توجہ مرکوز کرنے کے لئے ہر درجہ بندی کے تحت ظاہر ہونے والے اعداد و شمار کا تناسب کافی ہے۔

اس طرح کے امکانات P ((x Berdosaωi) کا حساب لگانا بہت مشکل ہے، کیونکہ یہ x ٹیسٹ سیٹ کے اعداد و شمار ہیں، تربیت کے سیٹ کے مطابق براہ راست نہیں مل سکے۔ اس کے بعد ہمیں تربیت کے سیٹ کے اعداد و شمار کی تقسیم کے قوانین کو تلاش کرنے کی ضرورت ہے، اور پھر ہم P ((x Berdosaωi) حاصل کریں گے۔

ذیل میں k قریبی ہمسایہ الگورتھم کا تعارف ہے، انگریزی میں KNN۔

ہم تربیت مرکب میں اعداد و شمار x1، x2 … xn (جن میں سے ہر ایک اعداد و شمار ہے m جہتی) کی بنیاد پر، کلاسωi کے تحت، ان اعداد و شمار کی تقسیم کو فٹ کرنے کے لئے چاہتے ہیں.

ہم جانتے ہیں کہ جب اعداد و شمار کی مقدار کافی بڑی ہو تو تناسب سے قریب تر امکان استعمال کیا جاسکتا ہے۔ اس اصول کا استعمال کرتے ہوئے ، نقطہ x کے گرد ، نقطہ x سے قریب ترین k نمونہ پوائنٹس تلاش کریں ، جن میں سے کوئی بھی زمرہ i کا ہے۔ اس k نمونہ پوائنٹ کے ارد گرد سب سے کم سپر بال کا حجم V کا حساب لگائیں؛ اور تمام نمونے کے اعداد و شمار میں سے نمبر نمبر نمبر حاصل کریں جو Ωi زمرے میں شامل ہیں۔

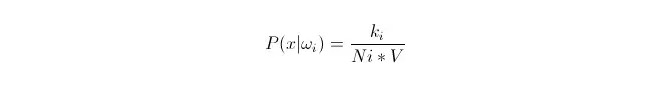
تو آپ دیکھ سکتے ہیں کہ ہم نے جو حساب لگایا ہے وہ دراصل کلسٹر شرائط کی کثافت ہے

P (ωi) کیا ہے؟ مندرجہ بالا طریقہ کار کے مطابق، P ((ωi) = Ni/N 。 جہاں N نمونوں کی کل تعداد ہے。 اس کے علاوہ، P (x) = k (n)*V) ، جہاں k اس سپر اسفیئر کے ارد گرد تمام نمونے کے پوائنٹس کی تعداد ہے؛ N نمونے کی کل تعداد ہے۔ تو P{\displaystyle {\displaystyle {\mathcal {P}}} i arrayx کا حساب لگایا جا سکتا ہے:

P(ωi|x)=ki/k

اس کے بعد ہم مندرجہ بالا مثال کی وضاحت کرتے ہیں، ایک V سائز کے سپر گولہ میں، k نمونوں کو گھیر لیا گیا ہے، جن میں سے کلاس i میں سے کوئی ایک ہے۔ اس طرح، جس قسم کے نمونوں کو گھیر لیا گیا ہے، ہم اس بات کا تعین کریں گے کہ یہاں x کس قسم کا ہونا چاہئے۔ یہ k قریبی پڑوسی الگورتھم کے ساتھ ڈیزائن کیا گیا درجہ بندی ہے۔