Verstecktes Markov-Modell

• ### 1. Kennenlernen

Heute wollen wir Ihnen zeigen, wie das HMM in einfacher Weise auf Aktien angewendet werden kann.

Wenn das Markov-Modell, das auf den ersten Blick hochwertig klingt, keine Ahnung hat, was es ist, dann lassen Sie uns einen Schritt zurückgehen und zuerst die Markov-Kette betrachten.

Die Markov-Kette, benannt nach Andrei Markov (A. A. Markov, 1856-1922) ist ein mathematischer Prozess von Markov-ähnlichen Zufälligkeiten. In einem gegebenen Zustand von aktuellem Wissen oder Information ist die Vergangenheit (d. h. der historische Zustand vor der Gegenwart) für die Vorhersage der Zukunft (d. h. der zukünftige Zustand nach der Gegenwart) irrelevant.

Jeder Zustandswechsel ist nur abhängig von den vorhergehenden n Zuständen. Dieser Prozess wird als ein Modell mit einer Größe von 1 n bezeichnet, wobei n die Anzahl der Zustände ist, die von den Zuständen beeinflusst werden. Der einfachste Markov-Prozess ist der Ein-Stufen-Prozess, bei dem jeder Zustandswechsel nur von dem vorhergehenden Staat abhängig ist.

• ### 2. Beispiel

In mathematischen Ausdrücken sieht es so aus:

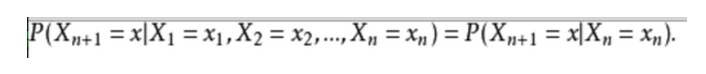
Ein Beispiel aus dem Alltag: Wir möchten das Wetter in der Zukunft anhand der aktuellen Wetterlage vorhersagen. Eine Möglichkeit ist die Annahme, dass jeder Zustand des Modells nur von dem vorhergehenden Zustand abhängig ist, die Markov-Annahme, die das Problem erheblich vereinfacht. Natürlich ist dieses Beispiel auch etwas unpraktisch.

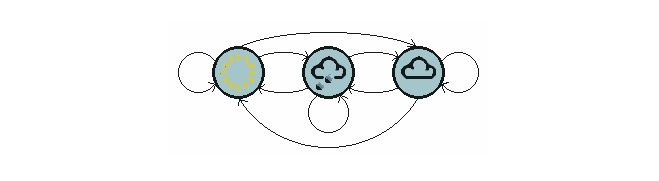
Die obige Grafik zeigt ein Modell der Wetterverschiebung.

Beachten Sie, dass ein einstufiger Prozess mit N Zuständen N2 Zustandswechsel hat. Die Wahrscheinlichkeit für jede Änderung wird als Zustandswechselwahrscheinlichkeit bezeichnet, d. h. die Wahrscheinlichkeit, dass ein Zustand von einem Zustand in einen anderen wechselt. Alle diese N2-Wahrscheinlichkeiten können mit einer Zustandswechselmatrix dargestellt werden, die in dem Beispiel des Wetters wie folgt aussieht:

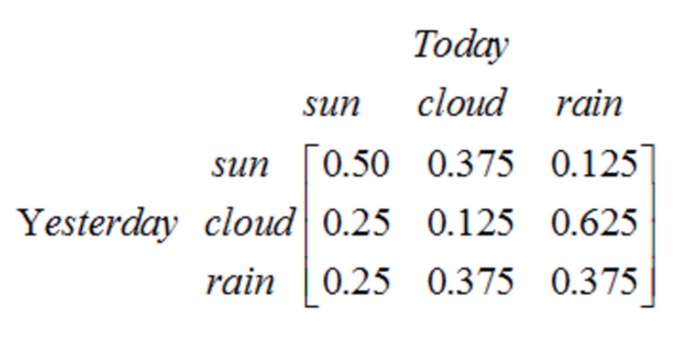
Diese Matrix gibt an, dass es eine 25%ige Wahrscheinlichkeit gibt, dass es heutzutage hell ist, wenn es gestern dunkel war, eine 12.5%ige Wahrscheinlichkeit, dass es dunkel ist, und eine 62.5%ige Wahrscheinlichkeit, dass es regnen wird.

Um ein solches System zu initialisieren, benötigen wir einen anfänglichen Wahrscheinlichkeitsvektor:

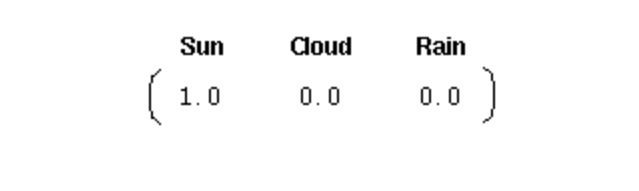
Dieser Vektor zeigt an, dass der erste Tag ein sonniger Tag war. Hier definieren wir die folgenden drei Teile für den oben genannten Markov-Prozess:

Die Lage: Sonnenschein, Nebel und Regen.

Der Anfangsvektor definiert die Wahrscheinlichkeit des Zustands des Systems, wenn die Zeit 0 ist.

Zustandsverlagerungsmatrix: Die Wahrscheinlichkeit jeder Wetterveränderung. Alle Systeme, die so beschrieben werden können, sind ein Markov-Prozess.

Was aber, wenn die Markov-Prozesse nicht stark genug sind? In manchen Fällen sind sie nicht ausreichend, um die Modelle zu beschreiben, die wir entdecken wollen.

Wenn wir beispielsweise nur die Börse beobachten, können wir nur Informationen über die Preise und Umsätze des Tages erhalten, aber wir wissen nicht, in welchem Zustand sich die Börse befindet (Bullmarkt, Bärenmarkt, Erschütterung, Bounce usw.). In diesem Fall haben wir zwei Zustandsgruppen, eine beobachtbare Zustandsgruppe (Preise und Umsätze der Börse usw.) und eine versteckte Zustandsgruppe (Stocksituation der Börse). Wir hoffen, einen Algorithmus zu finden, der die Lage der Börse anhand der Preise und Umsätze der Börse und der Markov-Hypothese prognostizieren kann.

In den oben genannten Fällen sind die Sequenzen der beobachtbaren und der verborgenen Zustände wahrscheinlichkeitsbezogen. Daher können wir diese Art von Prozess als ein verborgenes Markov-Prozess und eine Gruppe von Zuständen modellieren, die mit dieser verborgenen Markov-Prozess-Wahrscheinlichkeit verbunden sind und beobachtet werden können. Das ist das verborgene Markov-Modell.

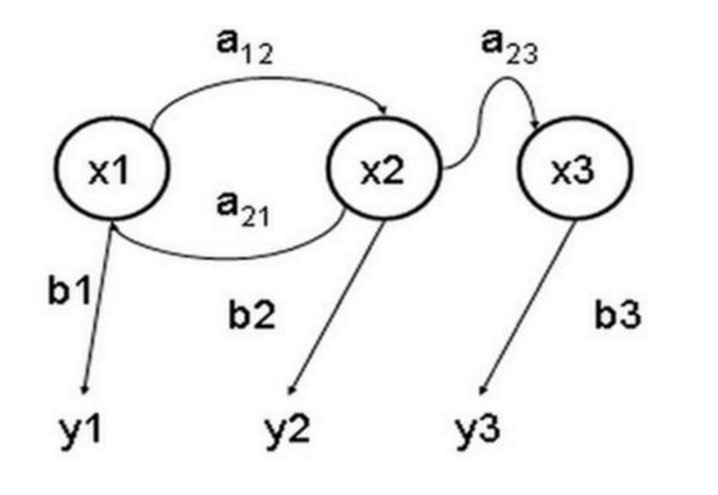
Das Hidden-Markov-Modell ist ein statistisches Modell, das verwendet wird, um ein Markov-Verfahren mit unbekannten impliziten Parametern zu beschreiben. Die Schwierigkeit besteht darin, die impliziten Parameter des Prozesses aus den beobachtbaren Parametern zu ermitteln und diese dann für eine weitere Analyse zu verwenden. Das folgende Bild ist ein Zustandstransfer-Diagramm des Hidden-Markov-Modells in drei Zuständen, in dem x den impliziten Zustand, y den beobachtbaren Ausgang, a die Wahrscheinlichkeit des Zustandstransfers und b die Wahrscheinlichkeit des Ausgangs darstellt.

Nehmen wir an, ich habe drei verschiedene Steine in der Hand. Der erste Stein ist ein gewöhnlicher Stein (d.h. D6), mit 6 Seiten, und die Wahrscheinlichkeit, dass jede Seite (d.h. 1,2,3,4,5,6) auftritt, ist ¹⁄₆. Der zweite Stein ist ein Vier-Seiten-System (d.h. D4), und die Wahrscheinlichkeit, dass jede Seite (d.h. 1,2,3,4) auftritt, ist ¹⁄₄. Der dritte Stein hat acht Seiten (d.h. D8), und die Wahrscheinlichkeit, dass jede Seite (d.h. 1,2,3,4,5,6,7,8) auftritt, ist ¹⁄₈.

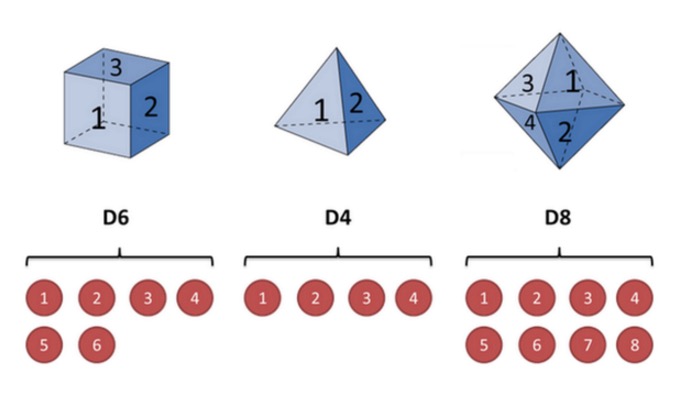
Angenommen, wir beginnen mit dem Stapel und wählen einen aus den drei Stapeln aus, wobei die Wahrscheinlichkeit, dass wir jeden Stapel auswählen, ¹⁄₃ ist. Dann werfen wir den Stapel und erhalten eine Zahl, eine von 1, 2, 3, 4, 5, 6, 7, 8.

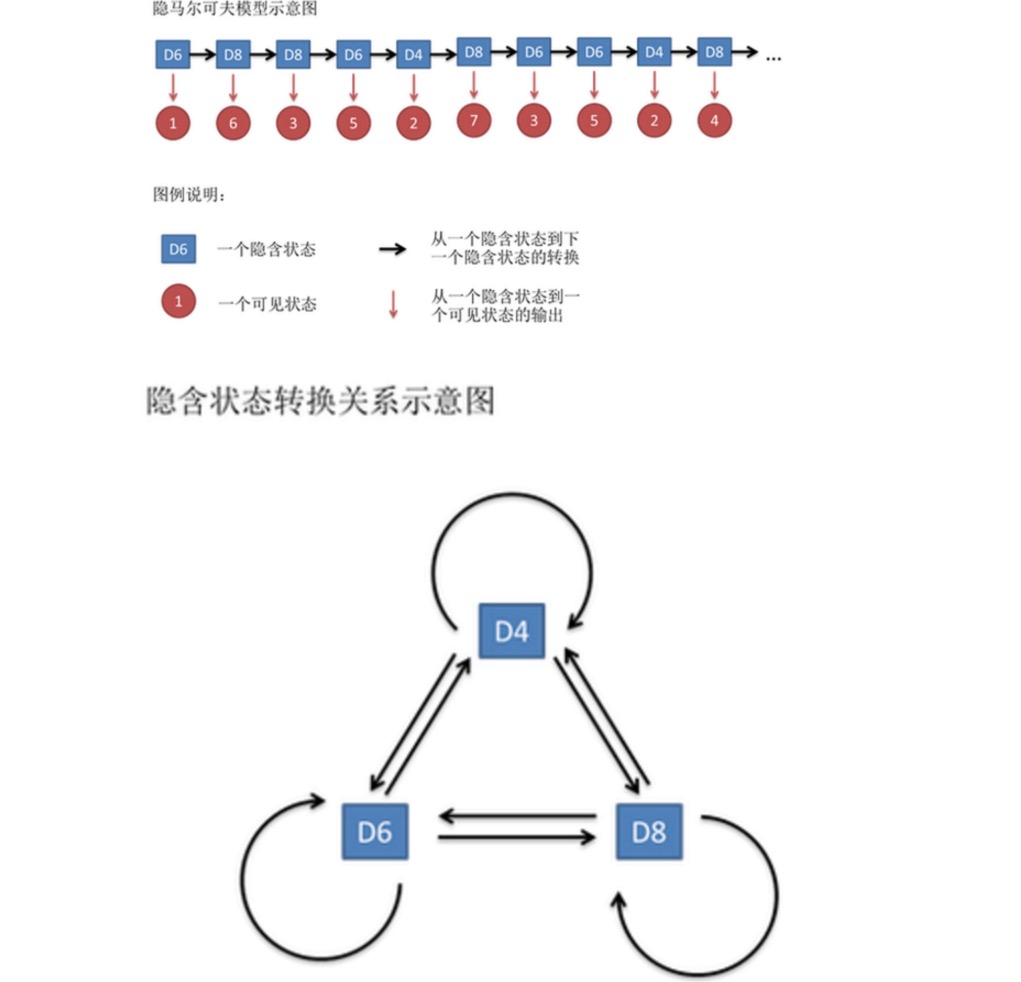
Diese Zahlen werden als sichtbare Zustandsketten bezeichnet. In einem Markov-Modell haben wir aber nicht nur diese Sichtbarkeitskette, sondern auch eine verborgene. In diesem Beispiel ist die verborgene Zustandskette die Reihenfolge der Sätze, die Sie verwenden.

Im Allgemeinen bezieht sich die Markov-Kette, von der in der HMM gesprochen wird, auf eine versteckte Zustandskette, da zwischen den versteckten Zuständen (Cuckoo) eine Umschaltwahrscheinlichkeit besteht. In unserem Beispiel ist der nächste Zustand von D6 D4, D6, D8 mit einer Wahrscheinlichkeit von ¹⁄₃. D4, D8, der nächste Zustand von D4, D6, D8 haben ebenfalls eine Umschaltwahrscheinlichkeit von ¹⁄₃.

Ebenso gibt es, obwohl es keine Umwandlungswahrscheinlichkeit zwischen den sichtbaren Zuständen gibt, eine Wahrscheinlichkeit zwischen den impliziten Zuständen und den sichtbaren Zuständen, die als Ausgabewahrscheinlichkeit bezeichnet wird. In unserem Beispiel ist die Ausgabewahrscheinlichkeit für die Sechsseitenkugel ((D6) 1 ¹⁄₆. Die Ausgabewahrscheinlichkeit für 2, 3, 4, 5, 6 ist ebenfalls ¹⁄₆.

Bei HMM ist es ziemlich einfach, Simulationen durchzuführen, wenn man im Voraus die Umrechnungswahrscheinlichkeit zwischen allen versteckten Zuständen und die Ausgabewahrscheinlichkeit zwischen allen versteckten Zuständen und allen sichtbaren Zuständen kennt. Bei der Anwendung eines HMM-Modells fehlt jedoch oft ein Teil der Information. Manchmal weiß man, wie viele Käse es gibt und was für eine Käse es ist, aber nicht, welche Käseserie herauskommt.

Die Algorithmen für das HMM-Modell sind in drei Kategorien unterteilt:

• Ich weiß, wie viele Käse es gibt (Anzahl der verborgenen Zustände), was jede Käse ist (Transformationswahrscheinlichkeit), was die Ergebnisse der Käse (sichtbare Zustandskette) sind, und ich möchte wissen, welche Käse jedes Mal (versteckte Zustandskette) herausgekommen sind.

• Ich möchte wissen, wie viele Käfige es gibt ((Anzahl der versteckten Zustände), was die Wahrscheinlichkeit ist, dass jedes Käfig ((Transformationswahrscheinlichkeit)) ist, und was die Wahrscheinlichkeit ist, dass das Ergebnis ((Anzahl der sichtbaren Zustandsketten)) ist.

• Da ich weiß, wie viele Käfige es gibt (die Anzahl der impliziten Zustände), nicht weiß, was jede Käfige ist (die Wahrscheinlichkeit der Umwandlung), und die Ergebnisse vieler Käfige beobachtet habe (die Kette der sichtbaren Zustände), möchte ich zurückschlagen, was jede Käfige ist (die Wahrscheinlichkeit der Umwandlung).

  Wenn wir die Probleme in der Börse lösen wollen, müssen wir Problem 1 und Problem 3 lösen. In einem nächsten Artikel werden wir sehen, wie das funktioniert.

Übertragung von Unbekannter Moneycode