Matemáticas y juego

• Sabemos que el juego de azar es un juego de probabilidades, y que algunos resultados extraños del juego despertaron el interés del matemático Pascal y el gran matemático Fermat, quienes, a través de un intercambio de cartas, propusieron algunos principios de la teoría de la probabilidad, lo que creó la teoría de la probabilidad.

• 1. El juego perfecto

Hay un partido entre los Lakers y los Cowboys de la NBA, y ambos equipos tienen fanáticos fieles, así que llámenlos los Tigres y los Cowboys. Los fanáticos, por supuesto, sienten que el equipo que apoyan tiene más probabilidades de ganar, por lo que están dispuestos a apostar con usted. Supongamos que los Tigres piensan que los Lakers tienen una probabilidad de ganar de p, y los Cowboys piensan que los Cowboys tienen una probabilidad de ganar de q, p y q.

El método es el siguiente: jugamos el mismo juego que el de los ratones de la tribu de los Ojos y el de los ratones de la tribu de los Búfalos, y si ganamos ganamos y, si perdemos perdemos x, siempre y cuando y> x. Y si x y y sólo tienen que satisfacer las siguientes dos inequidades simples, el rendimiento esperado de los ratones de la tribu de los Ojos y el de los ratones de la tribu de los Búfalos es positivo, y se juega con nosotros:

```
p * x - ( 1-p ) * y > 0
q * x - ( 1-q ) * y > 0
```

Con la restricción de que y > x, la imagen que se obtiene es el área rodeada por tres líneas rectas, y el valor de las coordenadas de cualquier punto en el interior (x, y) es una solución definitiva. Si p > q, la solución es la parte azul de la siguiente figura:

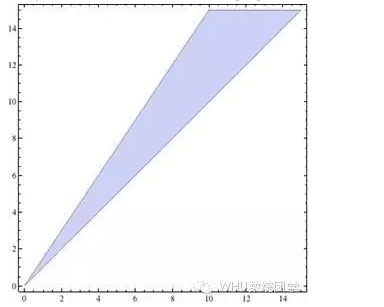
Parece que el problema está resuelto a la perfección, pero hay una duda, y creo que el lector pronto descubrirá su absurdo: si los monos de los orangutanes o los monos de los cocodrilos tienen una expectativa de ganancias positiva, es decir, ganan dinero a largo plazo, mientras que nosotros no, ¿de dónde viene todo ese dinero, y cómo es posible que todos ganen dinero?

• ### El truco de las dos o tres cartas

Este es otro juego ingenioso, en el que tenemos tres cartas: la carta número 1 es negra al revés, la carta número 2 es roja al revés, la carta número 3 es negra a un lado y la carta número 3 es roja al revés. Luego las ponemos en una caja, las sacudimos y dejamos que el oponente saque una carta plana sobre la mesa.

En realidad, la probabilidad de ganar no es ¹⁄₂, sino ²⁄₃, y lo que más desconcierta de este juego es la doble cara de las cartas. El jugador no saca 3 caras, sino 6 caras: 3 caras negras y 3 caras rojas. Las 6 caras son numeradas A, B, C, D, E, F:

Cuando el jugador tira a la cara negra, es decir, las tres posibilidades A, C y D, cuyas caras traseras son D, F y A, respectivamente, el caso negro representa ²⁄₃ .

El problema fue planteado por primera vez en 1889 por el matemático francés Joseph Louis François Bertrand, y debido a los resultados inesperados del problema, también se conoce como la paradoja de la caja de Bertrand. En 1950, el matemático estadounidense Warren Weaver introdujo el juego de cartas mencionado anteriormente, que Martin Gardner llamó el engaño de las tres cartas.

• ### 3 - La extraña ciruela A

Algunas veces en el juego empezamos con un poco de agua, dejamos que los demás ganen un poco de dinero, tiramos una cuerda larga y terminamos con la red. Este es un excelente ejemplo. Cuatro personas están jugando a bridge, y primero digo: “Vamos a jugar a las cartas, ahora tengo una A, ¿pueden adivinar si tengo más A? En este caso, es muy probable que pierda, en este caso, en su mente, se especifica una A de color, por ejemplo, A de cereza, y cuando una ronda de cereza A, esta es la oportunidad: “Juega a las cartas, ahora tengo una A de cereza, ¿pueden adivinar si no tengo más A de cereza?”

Mucha gente seguramente piensa que dos papas no son tan diferentes como una nuez negra, pero la diferencia entre ellos es increíble.

  没有A的情形：C（48，13）
  至少有1张A的情形：C（52，13）－C（48，13）
  恰好有1张A的情形：4＊C（48，12）
  至少有2张A的情形：C（52，13）－C（48，13）－4＊C（48，12）
  事件X为至少有两张A，事件Y为至少有一张A，那么条件概率为：

  P（X｜Y）＝P（XY）／P（Y）=(C（52，13）－C（48，13）－4＊C（48，12）)/(C（52，13）－C（48，13）)≈37%

En este momento tengo que ganarme a mí mismo y A, es más fácil de perder. Pero después de la colocación de la primera barra, la voluntad de apostar se movilizó, al ver la segunda barra o si se cambió de ropa, aumentaron las apuestas, y luego me dijeron que no tenía más A, en el medio de nosotros. A continuación, descubriremos que la probabilidad de la segunda barra es muy diferente:

  有黑桃A的情形：C（51，12）
  没有其它A的情形：C（48，12）
  还有其它A的情形：C（51，12）－C（48，12）
  事件X为还有其它A，事件Y为有黑桃A，条件概率为：

  P（X｜Y）＝P（XY）／P（Y）＝（C（51，12）－C（48，12））／C（51，12）≈56%。

Transcrito de la Unidad de Estadística de la WHU