Modelo oculto de Markov

• ### Conocimiento

Hoy vamos a hablar de la aplicación sencilla del HMM en las acciones.

El modelo de Markov oculto, que al principio suena muy sofisticado, no tiene ni idea de lo que es, así que vamos a dar un paso atrás y ver la cadena de Markov.

La cadena de Markov, llamada así por Andrei Markov (A. A. Markov, 1856-1922) es un proceso aleatorio de eventos aislados de naturaleza markovista en matemáticas. En el contexto de un conocimiento o información actual, el pasado (es decir, el estado histórico anterior al presente) es irrelevante para predecir el futuro (es decir, el estado futuro posterior al presente).

En este proceso, la transferencia de cada estado depende únicamente de los n estados anteriores, este proceso se conoce como modelo de 1 n grados, donde n es el número de estados de transferencia afectados. El proceso de Markov más simple es el proceso de un grado, donde la transferencia de cada estado depende únicamente del estado anterior.

• ### Ejemplo 2.

En términos matemáticos, esto es lo siguiente:

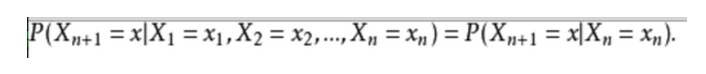
Para dar un ejemplo de la vida cotidiana, queremos predecir el tiempo futuro basándonos en la situación actual del tiempo. Una forma de hacerlo es asumir que cada estado del modelo depende únicamente del estado anterior, el supuesto de Markov, que simplifica enormemente el problema.

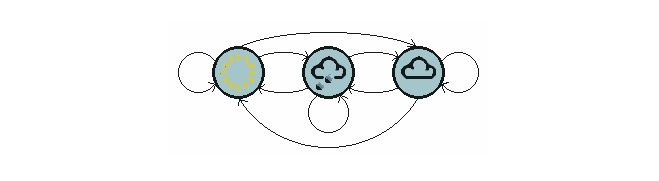
La imagen de arriba muestra un modelo de la transferencia del tiempo.

Observe que un proceso de una etapa que contiene N estados tiene N2 cambios de estado. La probabilidad de cada cambio se llama probabilidad de cambio de estado, es decir, la probabilidad de pasar de un estado a otro. Todas estas N2 probabilidades se pueden representar con una matriz de cambios de estado, la matriz de cambios de estado del ejemplo del clima anterior es la siguiente:

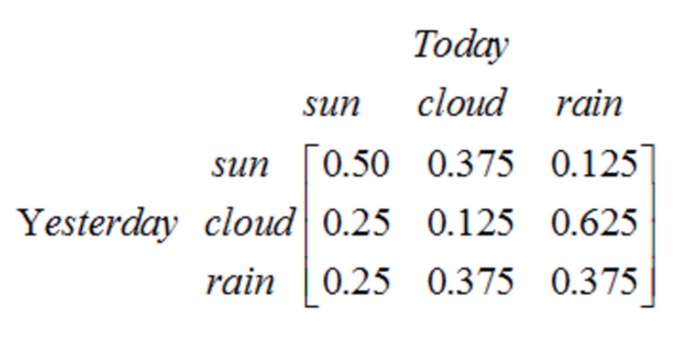
Esta matriz indica que si ayer fue nublado, entonces hoy tiene una probabilidad del 25% de ser un día soleado, una probabilidad del 12.5% de ser un día nublado, y una probabilidad del 62.5% de que llueva. Obviamente, la suma de cada línea de la matriz es 1 .

Para initializar un sistema así, necesitamos un vector de probabilidad inicial:

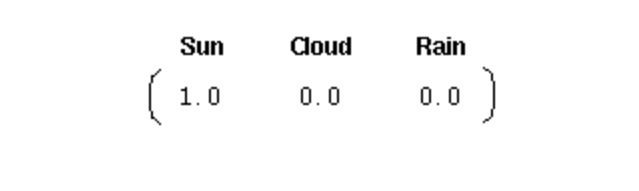
Este vector indica que el primer día fue un día soleado. Aquí, definimos las siguientes tres partes para el proceso de Markov de primer grado:

El estado: Cielo despejado, nublado y lluvia.

Vector inicial: define la probabilidad del estado del sistema cuando el tiempo es 0.

Matriz de transferencia de estado: probabilidad de cada cambio climático. Todos los sistemas que pueden describirse de esta manera son un proceso de Markov.

Sin embargo, ¿qué hacemos cuando el proceso de Markov no es lo suficientemente potente? En algunos casos, el proceso de Markov no es suficiente para describir los patrones que queremos encontrar.

Por ejemplo, en nuestro mercado de valores, si solo observamos el mercado, solo podemos conocer información sobre el precio, el volumen de transacciones y otros datos del día, pero no sabemos qué estado se encuentra el mercado de valores en ese momento (bull market, bear market, oscilación, rebote, etc.). En este caso, tenemos dos conjuntos de estados, un conjunto de estados observables (estado de transacción del precio del mercado de valores, etc.) y un conjunto de estados ocultos (estado del mercado de valores). Esperamos encontrar un algoritmo que pueda predecir el estado del mercado de valores en función del estado de transacción del precio del mercado de valores y la hipótesis de Markov.

En los casos anteriores, la secuencia de estados observables y la secuencia de estados ocultos son probables. Por lo tanto, podemos modelar este tipo de proceso como un proceso de Markov oculto y un conjunto de estados observables y relacionados con la probabilidad de este proceso de Markov oculto, el modelo de Markov oculto.

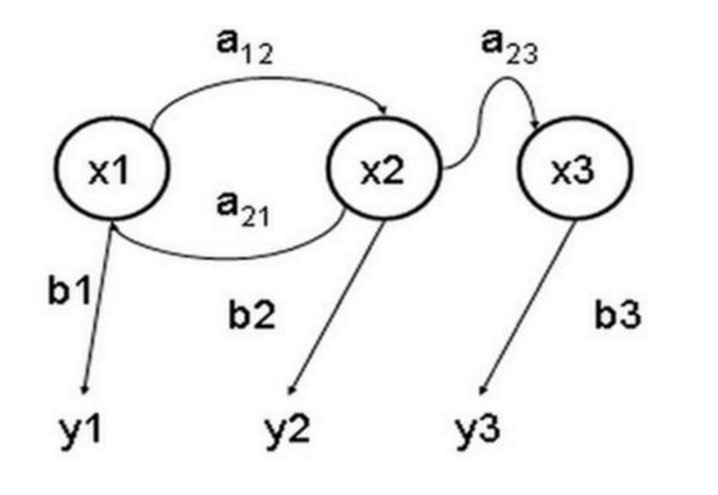
El modelo de Markov oculto es un modelo estadístico para describir un proceso de Markov que contiene parámetros desconocidos ocultos. La dificultad consiste en determinar los parámetros ocultos del proceso a partir de los parámetros observables, y luego utilizar estos parámetros para realizar un análisis posterior. El siguiente gráfico es un gráfico de transferencia de estado del modelo de Markov oculto de tres estados, donde x representa el estado oculto, y representa la salida observable, a representa la probabilidad de conversión de estado y b representa la probabilidad de salida.

Para ilustrar esto con el ejemplo de un conejo: supongamos que tengo en la mano tres conejos diferentes. El primer conejo es nuestro conejo común (llamemos a este conejo D6), con 6 caras, y la probabilidad de que aparezca cada una de las caras es ¹⁄₆. El segundo conejo es un cuadrúpedo (llamemos a este conejo D4), y la probabilidad de que aparezca cada una de las caras es ¹⁄₄. El tercer conejo tiene ocho caras (llamemos a este conejo D8), y la probabilidad de que aparezca cada una de las caras es ¹⁄₈.

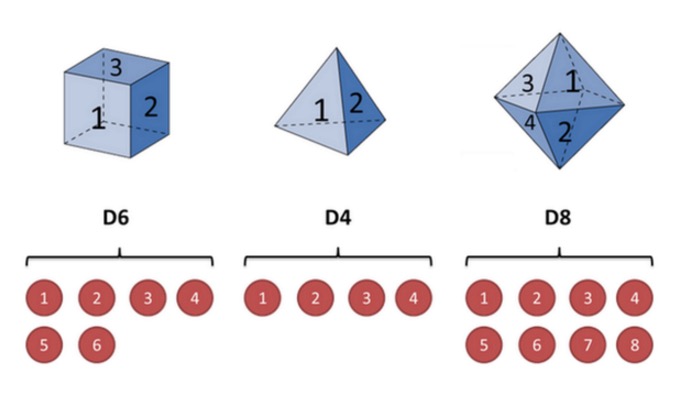
Supongamos que comenzamos con la cuña, elegimos una de las tres cuñas, y la probabilidad de elegir cada una de las cuñas es de ¹⁄₃. Luego, la cuña, obteniendo un número, 1, 2, 3, 4, 5, 6, 7, 8.

Esta serie de números se llama cadena de estados visibles. Pero en el modelo de Hidden Markov, no solo tenemos una cadena de estados visibles, sino también una cadena de estados ocultos. En este ejemplo, la cadena de estados ocultos es la secuencia de cuerdas que usas. Por ejemplo, la cadena de estados ocultos podría ser:

En general, la cadena de Markov que se menciona en HMM es una cadena de estados ocultos, ya que existe una probabilidad de conversión entre los estados ocultos ((cubo)). En nuestro ejemplo, el siguiente estado de D6 es D4, D6, D8 tiene una probabilidad de 1 / 3. D4, D8, el siguiente estado es D4, D6, D8 tiene una probabilidad de conversión de 1 / 3.

Del mismo modo, aunque no hay una probabilidad de conversión entre los estados visibles, hay una probabilidad entre los estados implícitos y los estados visibles llamada probabilidad de salida. En nuestro ejemplo, la probabilidad de salida de un cubo de seis caras (D6) es ¹⁄₆. La probabilidad de salida de un cubo de seis caras (D6) es ¹⁄₆.

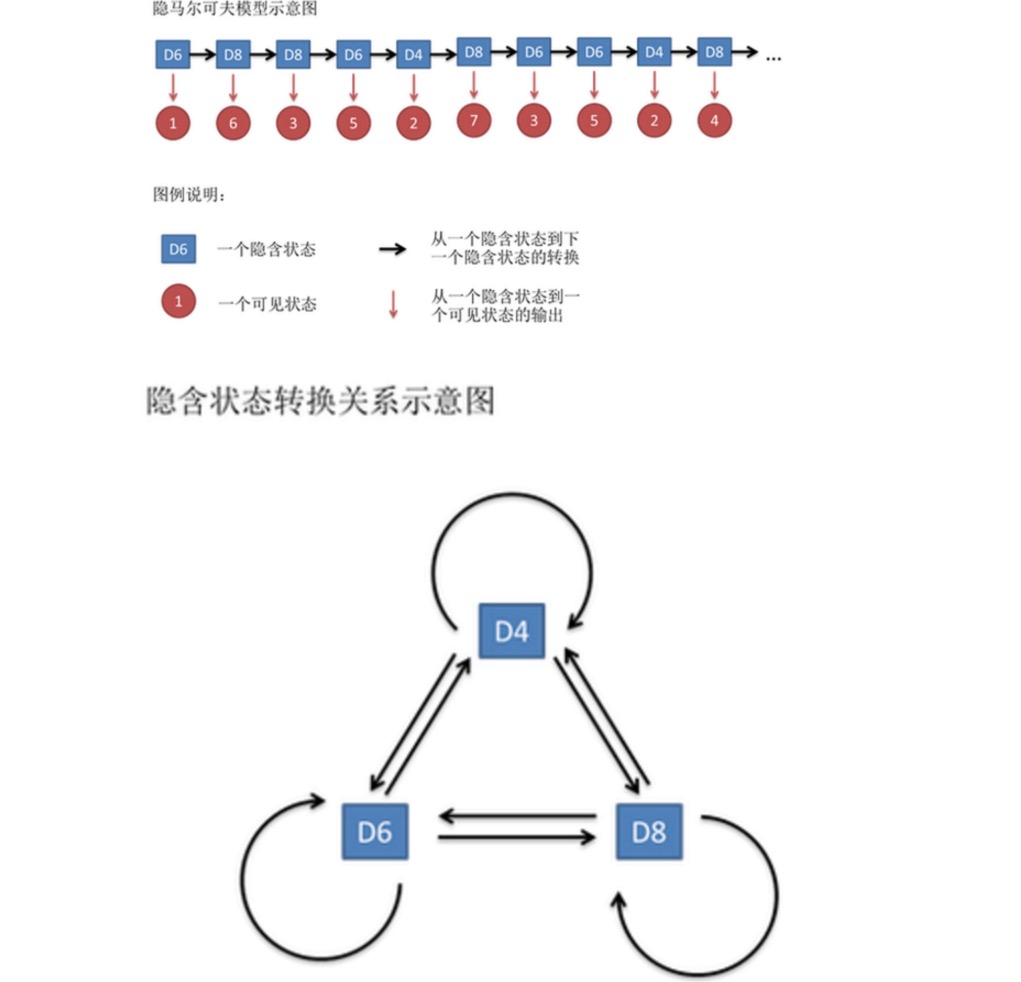
En realidad, para HMM, hacer simulaciones es bastante fácil si se conoce de antemano la probabilidad de conversión entre todos los estados ocultos y la probabilidad de salida entre todos los estados ocultos y todos los estados visibles. Pero cuando se aplica el modelo HMM, a menudo falta parte de la información, a veces se sabe cuántos gatos hay y cuál es cada tipo de conejo, pero no se sabe la secuencia de conejos que se obtienen; a veces solo se ven los resultados de los gatos muchas veces y no se sabe nada más. Si se aplica un algoritmo para estimar esta información perdida, se convierte en un problema muy importante.

Los algoritmos relacionados con el modelo HMM se dividen en tres categorías principales, que resuelven tres tipos de problemas:

• Saber cuántos gatos hay (número de estados implicados), qué es cada tipo de gatos (probabilidad de conversión), según el resultado de la extracción de los gatos (cadena de estados visibles), me gustaría saber qué tipo de gatos salen cada vez (cadena de estados implicados).

• ¿Cuántos tipos de cuerdas hay? ¿cuántos estados ocultos? ¿cuál es la probabilidad de conversión? ¿cuál es la probabilidad de obtener este resultado?

• Saber cuántos tipos de cuerdas hay (número de estados implicados), no saber cuál es cada tipo de cuerdas (probabilidad de conversión), observar el resultado de muchas cuerdas (cadena de estados visibles), quiero deducir cuál es cada tipo de cuerdas (probabilidad de conversión).

  Si queremos resolver el problema de la bolsa de valores, necesitamos resolver el problema 1 y el problema 3, y en el próximo artículo veremos cómo hacerlo.

Transcrito de la columna No sé qué es Moneycode