수학과 도박

• 우리는 도박이 확률의 게임이라는 것을 알고 있습니다. 또한 몇 가지 이상한 도박 결과는 수학자 파스칼 (Pascal) 과 위대한 수학자 페르마 (Fermat) 의 관심을 불러일으켰습니다. 그들은 편지를 통해 확률 이론의 몇 가지 원칙을 제시하여 확률 이론을 창설했습니다.

• 1. 완벽한 도박

NBA 팀인 레이커스 팀과 소牛 팀의 한 경기가 있고, 두 팀 모두 충성스러운 팬이 있는데, 그들을 인족 과 牛族 이라고 불러주세요. 팬들은 당연히 자신이 지지하는 팀이 더 이길 가능성이 있다고 생각해서 기꺼이 당신과 도박을 합니다. 인족 이 레이커스의 승률이 p라고 생각하고, 牛族 이 소牛族의 승률이 q,p,q라고 생각하고 모두 50% 이상이어야 합니다. 다음은 재미있는 부분입니다. 우리는 항상 쉽게 인족 과 牛族을 상대로 경기를 할 수 있는 방법을 고안할 수 있지만, 결과가 어떻든, 우리는 잘 지을 수 있습니다!

이 방법은 다음과 같습니다. 우리는 각각 족 과 牛族 과 같은 을 치고, 우리가 이긴다면 y 元을 얻으며, 잃으면 x 元을 잃어, y>x 가 되면 우리는 한다. 그리고 x와 y는 다음의 두 가지 간단한 부등식을 만족시켜야 합니다. 족 과 牛族 의 기대 수익이 양이 되면, 우리에게 을 치게 됩니다:

```
p * x - ( 1-p ) * y > 0
q * x - ( 1-q ) * y > 0
```

y>x의 제한을 더하면, 그려진 이미지는 세 개의 직선으로 둘러싸인 영역이며, 그 안의 임의의 점의 좌표값 ((x, y) 은 반드시 필요한 해결책이다. p>q라면, 해는 아래 그림의 파란색 부분이다:

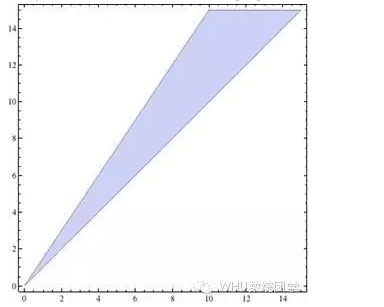
이 문제는 완벽하게 해결된 것처럼 보이지만, 한 가지 의문점이 있습니다. 독자들은 곧 이 문제의 터무니없음을 알게 될 것입니다. 양족의 양이나 양소족의 양이 모두 긍정적인 수익을 기대하고 있습니다. 즉, 장기적으로 볼 때, 그들은 돈을 벌고, 우리는 안정적으로 수익을 올리고 있습니다.

• ### 2장 3장의 사기

이것은 또 다른 기발한 퍼즐입니다. 우리는 먼저 3개의 카드를 준비합니다. 1번의 카드는 앞면이 모두 검은색이고, 2번의 카드는 앞면이 모두 빨간색이고, 3번의 카드는 한쪽은 검은색이고, 한쪽은 빨간색입니다. 그리고는 카드를 한 상자에 넣고, 흔들고, 상대방이 평면 하나를 뽑아 테이블 위에 놓습니다. 그리고는 그와 의 반대면이 같은 색과正面을 가지고 있습니다. 이 퍼즐은 공평한 것처럼 보입니다. 예를 들어, 표면이 검은색인 카드가 뽑히면, 카드는 1번이 아닌 3번이고, 반대면이 검은색이 아닌 빨간색이고, 직관적으로 각각 1/2의 확률입니다.

사실 우리가 이기는 확률은 1/2이 아니라 2/3입니다. 이 게임에서 가장 혼란스러운 점은 카드의 두면성이라는 점입니다. 플레이어가 뽑는 것은 3개의 카드가 아니라 6개의 카드가 있습니다. 3개의 검은면, 3개의 빨간면입니다. 우리는 이 6개의 면을 A, B, C, D, E, F로 숫자로 씁니다.

플레이어가 검은 면을 뽑으면, A, C, D 세 가지의 가능한 상황이며, 그들의 뒷면은 각각 D, F, A이며, 검은 색의 경우는 2/3를 차지한다.

이 문제는 1889년 프랑스의 수학자 베르트랑 (Joseph Louis François Bertrand) 에 의해 처음 제기되었으며, 이 문제의 결과가 예상치 못했기 때문에, 베르트랑의 상자 역설 (Bertrand’s box paradox) 이라고도 불린다. 1950년 미국의 수학자 워렌 웨이버 (Warren Weaver) 는 위의 카드 플레이를 소개했고, 마틴 가드너 (Martin Gardner) 는 이를 삼카드 사기 (three-card swindle) 라고 부른다.

• ### 3 아주 특이한 桃 A

때때로 우리는 도박을 시작하면 물을 내리고, 다른 사람들이 먼저 약간의 돈을 벌고, 긴 줄을 어 큰 물고기를 잡고, 마지막으로 하나의 망을 끝냅니다. 아래는 훌륭한 예입니다. 네 명이 브리지 카드를 치고 있는데, 나는 먼저 말합니다. “ 와서 을 치고, 나는 이제 A를 가지고있다, 당신은 내가 더 많은 A를 가지고 있는지 짐작 할 수 있습니까? 이런 상황에서 당신은 잃을 가능성이 높습니다. 당신은 마음속으로는 꽃 A를 지정합니다. 예를 들어, 검은 A, 어떤 라운드에서 검은 A를 잡은 후, 기회가 왔습니다. “ 다시 을 치고, 나는 이제 검은 A를 가지고 있고, 당신은 내가 더 많은 A를 가지고 있지 않은지 짐작 할 수 있습니까?”

많은 사람들이 두 개의 이 전혀 다르지 않다고 생각할 것입니다. 하지만 그 둘 사이의 차이는 믿을 수 없을 정도로 크다. 첫번째 의 확률을 계산해 봅시다.

  没有A的情形：C（48，13）
  至少有1张A的情形：C（52，13）－C（48，13）
  恰好有1张A的情形：4＊C（48，12）
  至少有2张A的情形：C（52，13）－C（48，13）－4＊C（48，12）
  事件X为至少有两张A，事件Y为至少有一张A，那么条件概率为：

  P（X｜Y）＝P（XY）／P（Y）=(C（52，13）－C（48，13）－4＊C（48，12）)/(C（52，13）－C（48，13）)≈37%

이 때 나는 나 자신에게 A를 더 주고, 상대적으로 잃는 것이 쉽다. 그러나 첫 번째 을 세운 후, 모든 사람들의 도박 의지가 동원되었다. 두 번째 이 옷을 갈아입은 것 아니냐는 것을 보고, 더 큰 도박을 했다, 그리고 나는 더 많은 A를 가지고 있지 않다. 바로 우리 아래에서. 다음에는 두 번째 의 확률이 크게 다르다는 것을 알게 될 것입니다.

  有黑桃A的情形：C（51，12）
  没有其它A的情形：C（48，12）
  还有其它A的情形：C（51，12）－C（48，12）
  事件X为还有其它A，事件Y为有黑桃A，条件概率为：

  P（X｜Y）＝P（XY）／P（Y）＝（C（51，12）－C（48，12））／C（51，12）≈56%。

WHU 통계학