Model Markov Tersembunyi

• ### 1. Kenali

Hari ini kita akan membincangkan mengenai aplikasi mudah HMM dalam saham.

Model Markov yang tersembunyi, yang pada mulanya terdengar canggih, tidak tahu apa-apa, jadi mari kita kembali ke belakang dan lihat rantaian Markov.

Rantaian Markov, yang dinamakan sempena Andrei Markov (A.A. Markov, 1856-1922) (iaitu orang di bawah), merujuk kepada proses acak kejadian berasingan yang bersifat Markovik dalam matematik. Dalam keadaan pengetahuan atau maklumat semasa yang diberikan, masa lalu (iaitu keadaan sejarah sebelum masa kini) tidak relevan untuk meramalkan masa depan (iaitu keadaan masa depan selepas masa kini).

Dalam proses ini, perpindahan setiap keadaan hanya bergantung pada keadaan sebelumnya, proses ini dikenali sebagai model 1n-kelas, di mana n adalah bilangan keadaan yang mempengaruhi perpindahan. Proses Markov yang paling mudah adalah proses satu-kelas, di mana setiap perpindahan keadaan hanya bergantung pada keadaan sebelumnya.

• ### Kedua, contoh

Dalam ungkapan matematik, ia adalah seperti berikut:

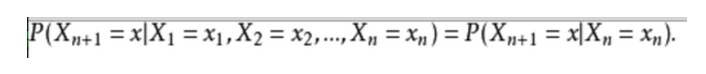
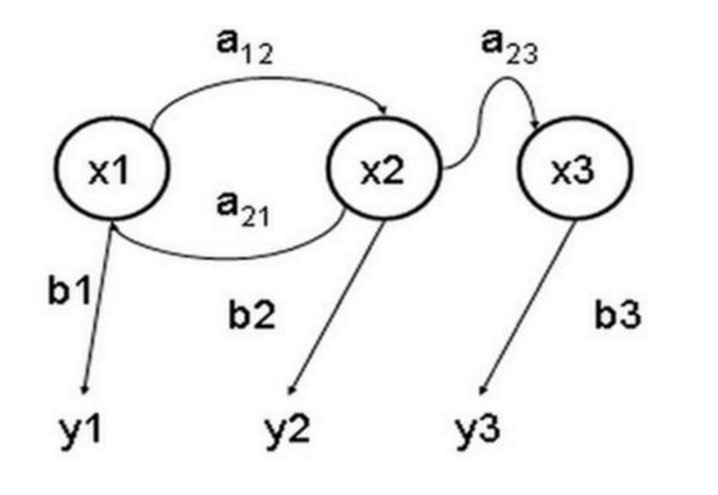
Sebagai contoh dalam kehidupan seharian, kita ingin meramalkan keadaan cuaca masa depan berdasarkan keadaan cuaca semasa. Salah satu cara adalah dengan mengandaikan bahawa setiap keadaan dalam model ini hanya bergantung pada keadaan yang sebelumnya, iaitu hipotesis Markov, yang sangat menyederhanakan masalah ini.

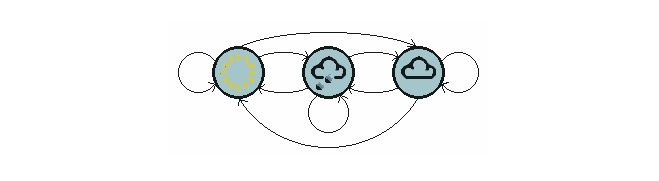
Gambar di atas menunjukkan model perubahan cuaca.

Perhatikan bahawa proses satu peringkat yang mengandungi N keadaan mempunyai N2 perpindahan keadaan. Probabiliti setiap perpindahan dipanggil kebarangkalian perpindahan keadaan, iaitu kebarangkalian perpindahan dari satu keadaan ke keadaan yang lain. Semua N2 kebarangkalian ini boleh dinyatakan dengan matriks perpindahan keadaan, matriks perpindahan keadaan contoh cuaca di atas adalah seperti berikut:

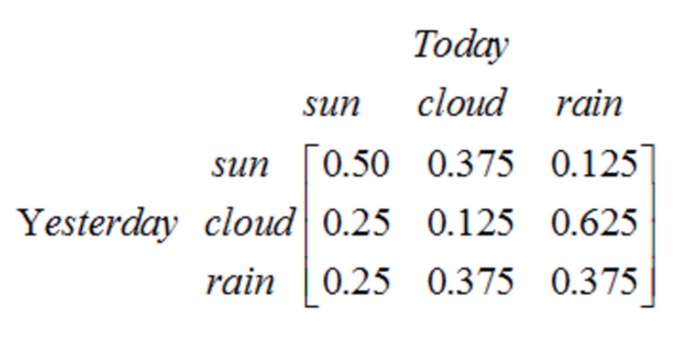
Matriks ini menyatakan bahawa jika semalam adalah hari yang mendung, maka hari ini mempunyai 25% kemungkinan hari yang cerah, 12.5% kemungkinan hari yang mendung, dan 62.5% kemungkinan hujan, dengan jelas, jumlah setiap baris dalam matriks adalah 1.

Untuk menginisialisasi sistem seperti ini, kita memerlukan vektor kebarangkalian awal:

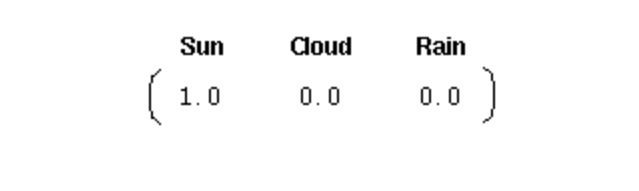
Vektor ini menunjukkan bahawa hari pertama adalah hari yang cerah. Di sini, kita menentukan tiga bahagian berikut untuk proses Markov satu peringkat di atas:

Keadaan: cerah, mendung dan hujan.

Vektor awal: menentukan kebarangkalian keadaan sistem pada masa 0.

Matriks peralihan keadaan: kebarangkalian setiap peralihan cuaca. Semua sistem yang dapat digambarkan sedemikian adalah proses Markov.

Namun, apa yang perlu kita lakukan apabila proses Markov tidak cukup kuat? Dalam beberapa kes, proses Markov tidak cukup untuk menggambarkan model yang kita mahu temui.

Sebagai contoh, di pasaran saham kita, jika hanya mengamati pasaran, kita hanya dapat mengetahui harga, jumlah dagangan dan lain-lain maklumat hari itu, tetapi tidak tahu apa keadaan pasaran saham pada masa ini (bull market, bear market, goyah, rebound, dan lain-lain), dalam hal ini kita mempunyai dua set keadaan, satu set keadaan yang dapat dilihat (price trading, dan lain-lain) dan satu set keadaan tersembunyi (status pasaran saham). Kami berharap dapat mencari algoritma yang dapat meramalkan keadaan pasaran saham berdasarkan keadaan harga dan jumlah dagangan di pasaran saham dan hipotesis Markov.

Dalam kes-kes di atas, urutan keadaan yang dapat dilihat dan urutan keadaan yang tersembunyi adalah berkemungkinan berkaitan. Oleh itu, kita boleh memodelkan proses jenis ini sebagai satu proses Markov tersembunyi dan satu set keadaan yang berkaitan dengan kemungkinan proses Markov tersembunyi dan dapat dilihat, iaitu model Markov tersembunyi.

Hidden Markov Model ialah satu model statistik yang digunakan untuk menggambarkan suatu proses Markov yang mengandungi parameter yang tidak diketahui yang tersembunyi. Yang sukar adalah untuk menentukan parameter tersembunyi proses dari parameter yang boleh diperhatikan, dan kemudian menggunakan parameter tersebut untuk analisis lanjut.

Sebagai contoh, andaikan saya mempunyai tiga buah keling yang berbeza. Keling pertama adalah keling biasa kita (sebutlah keling ini D6), dengan 6 muka, setiap muka (sebutlah keling ini D4) mempunyai peluang ¹⁄₆. Keling kedua ialah keling empat muka (sebutlah keling ini D4) mempunyai peluang ¹⁄₄. Keling ketiga mempunyai lapan muka (sebutlah keling ini D8) dan setiap muka (sebutlah keling ini D8) mempunyai peluang ¹⁄₈.

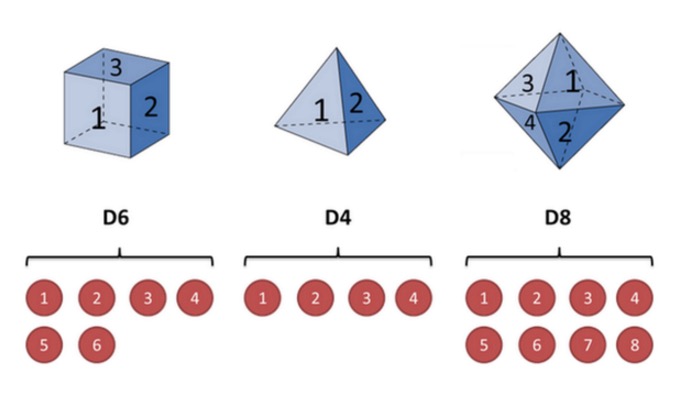
Katakanlah kita mulakan dengan mengundi, kita pilih satu daripada tiga undi, dan peluang untuk setiap undi adalah ¹⁄₃. Kemudian kita undi, dan kita dapat satu nombor, 1, 2, 3, 4, 5, 6, 7, 8. Berterus-terus mengulangi proses di atas, kita akan mendapat satu siri nombor, dan setiap nombor adalah satu daripada 1, 2, 3, 4, 5, 6, 7, 8.

Senarai ini dipanggil rantaian keadaan yang kelihatan. Tetapi dalam model Markov tersirat, kita tidak hanya mempunyai rantaian keadaan yang kelihatan, tetapi juga rantaian keadaan tersirat. Dalam contoh ini, rantaian keadaan tersirat adalah urutan yang anda gunakan.

Secara umum, rantaian Markov yang dikatakan dalam HMM sebenarnya merujuk kepada rantaian keadaan tersembunyi, kerana terdapat kebarangkalian peralihan antara keadaan tersembunyi ((tikung)). Dalam contoh kami, keadaan seterusnya D6 adalah D4, D6, D8 kebarangkalian adalah 1 / 3. D4, D8 kebarangkalian seterusnya adalah D4, D6, D8 kebarangkalian peralihan adalah 1 / 3.

Begitu juga, walaupun tidak ada kebarangkalian untuk menukar antara keadaan yang kelihatan, tetapi terdapat kebarangkalian antara keadaan yang tersirat dan keadaan yang kelihatan yang dipanggil kebarangkalian output. Dalam contoh kita, kotak enam muka (D6) menghasilkan 1 dengan kebarangkalian output ¹⁄₆. Kebarangkalian menghasilkan 2, 3, 4, 5, 6 juga ¹⁄₆. Kita juga boleh membuat definisi lain untuk kebarangkalian output.

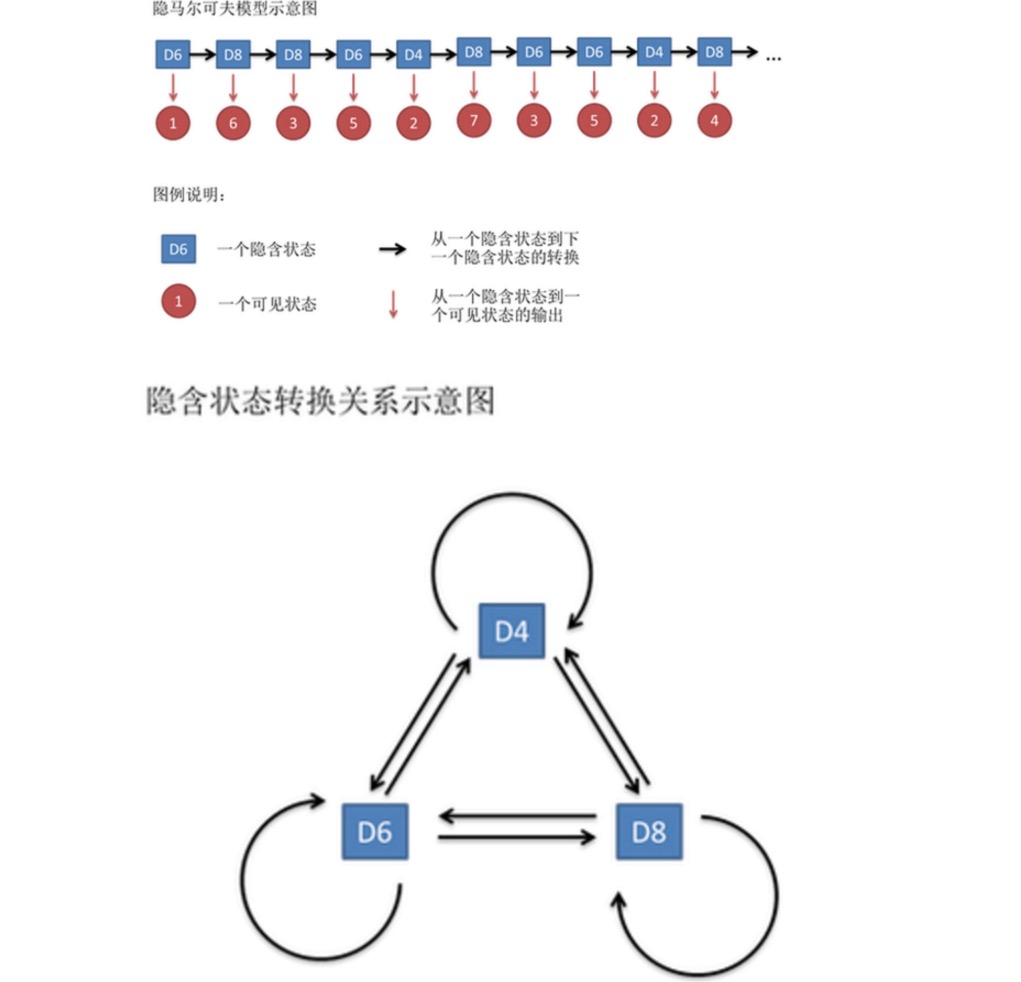
Sebenarnya untuk HMM, jika anda mengetahui kebarangkalian penukaran antara semua keadaan tersembunyi dan kebarangkalian output antara semua keadaan tersembunyi ke semua keadaan yang kelihatan, melakukan simulasi adalah agak mudah. Tetapi apabila menggunakan model HMM, sebilangan maklumat sering hilang, kadang-kadang anda tahu berapa banyak keping, apa yang setiap keping, tetapi tidak tahu urutan keping yang dikeluarkan; kadang-kadang anda hanya melihat hasil keping berkali-kali, dan tidak tahu apa-apa yang lain.

Algoritma yang berkaitan dengan model HMM terbahagi kepada tiga kategori, masing-masing menyelesaikan tiga jenis masalah:

• Mengetahui berapa banyak jenis pautan (bilangan keadaan tersembunyi), apa setiap pautan (probabiliti penukaran), berdasarkan hasil pautan (rangkaian keadaan yang kelihatan), saya ingin tahu apa jenis pautan yang dikeluarkan setiap kali (rangkaian keadaan tersembunyi).

• Saya juga ingin tahu berapa banyak jenis pautan yang terdapat (jumlah keadaan tersirat), apa setiap jenis pautan (probabiliti penukaran), dan berdasarkan hasil yang dikeluarkan oleh pautan (rantai keadaan yang kelihatan), saya ingin tahu kebarangkalian hasil yang dikeluarkan.

• Mengenal berapa banyak jenis pautan ((bilangan keadaan tersirat), tidak tahu apa setiap jenis pautan ((probabiliti penukaran), mengamati hasil banyak kali pautan ((rantai keadaan yang kelihatan), saya ingin mencadangkan apa setiap jenis pautan ((probabiliti penukaran)).

  Jika kita mahu menyelesaikan masalah dalam pasaran saham di atas, kita perlu menyelesaikan soalan 1 dan soalan 3, dan dalam artikel seterusnya kita akan melihat bagaimana untuk melakukannya.

Dipetik dari Kenali Moneycode