Mô hình Markov ẩn

• ### 1. Biết

Hôm nay chúng tôi sẽ giới thiệu một cách đơn giản về HMM (Mô hình Markov ẩn) trong chứng khoán.

Mô hình Markov ẩn giấu, nghe có vẻ cao cấp, nhưng không biết nó là gì, vậy hãy lùi lại một bước và xem chuỗi Markov.

Chuỗi Markov, được đặt tên theo Andrey Markov (A.A. Markov, 1856-1922) (đó là người bên dưới), là một quá trình ngẫu nhiên của sự kiện phân ly có tính chất Markov trong toán học. Trong trường hợp có kiến thức hoặc thông tin hiện tại, quá khứ (tức là trạng thái lịch sử trước hiện tại) không liên quan đến dự đoán tương lai (tức là trạng thái tương lai sau hiện tại).

Trong quá trình này, chuyển đổi của mỗi trạng thái chỉ phụ thuộc vào n trạng thái trước đó, quá trình này được gọi là mô hình 1 n cấp, trong đó n là số lượng các trạng thái chuyển đổi ảnh hưởng. Quá trình Markov đơn giản nhất là quá trình một cấp, mỗi chuyển đổi của trạng thái chỉ phụ thuộc vào trạng thái trước đó.

• ### Ví dụ 2.

Các nhà khoa học đã tìm ra cách để giải thích các vấn đề này bằng cách sử dụng các biểu thức toán học như sau:

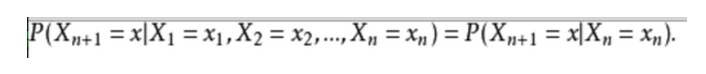
Một ví dụ trong cuộc sống hàng ngày, chúng ta muốn dự đoán thời tiết trong tương lai dựa trên tình trạng thời tiết hiện tại. Một cách để làm điều này là giả định rằng mỗi trạng thái của mô hình này chỉ phụ thuộc vào trạng thái trước đó, giả định Markov, giả định này có thể đơn giản hóa vấn đề rất nhiều. Dĩ nhiên, ví dụ này cũng không thực tế.

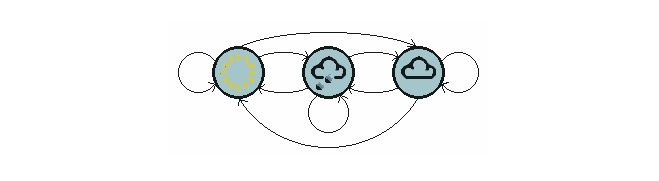
Hình trên cho thấy mô hình chuyển đổi thời tiết.

Lưu ý rằng một quá trình một bước có N trạng thái có N2 chuyển trạng thái. Mỗi xác suất chuyển được gọi là xác suất chuyển trạng thái, tức là xác suất chuyển từ trạng thái này sang trạng thái khác. Tất cả các xác suất N2 này có thể được biểu thị bằng ma trận chuyển trạng thái, ma trận chuyển trạng thái của ví dụ thời tiết trên như sau:

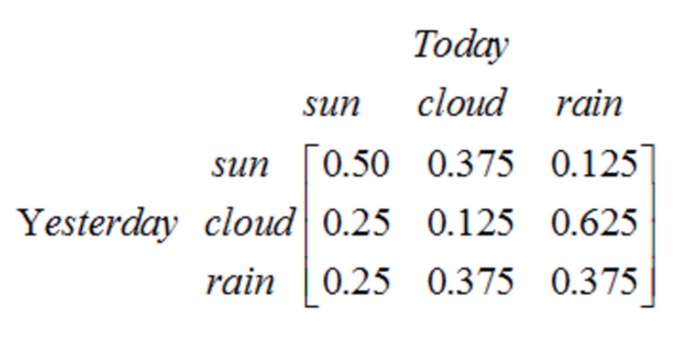
Bảng ma trận này cho biết rằng nếu ngày hôm qua có nhiều mây, thì ngày hôm nay có 25% khả năng là trời sáng, 12,5% khả năng là trời nhiều mây, 62,5% khả năng là trời mưa, và rõ ràng là tổng của mỗi hàng trong ma trận là 1.

Để khởi tạo một hệ thống như vậy, chúng ta cần một vector xác suất khởi tạo:

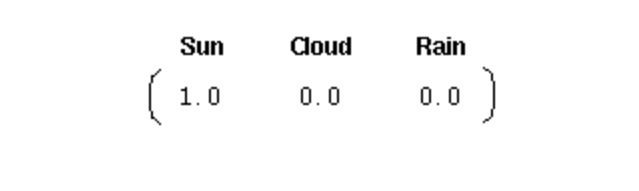
Đây là vector cho ngày đầu tiên là ngày đẹp trời. Ở đây, chúng ta đã xác định ba phần sau cho quá trình Markov một cấp trên:

Tình trạng: Trời rực rỡ, trời u ám và mưa

Vector ban đầu: xác định xác suất của trạng thái của hệ thống khi thời gian là 0.

Ma trận chuyển trạng thái: xác suất của mỗi biến đổi thời tiết. Tất cả các hệ thống có thể được mô tả như vậy là một quá trình Markov.

Tuy nhiên, khi quá trình Markov không đủ mạnh mẽ, chúng ta phải làm gì? Trong một số trường hợp, quá trình Markov không đủ mạnh để mô tả các mô hình mà chúng ta muốn tìm thấy.

Ví dụ như thị trường chứng khoán của chúng ta, nếu chỉ quan sát thị trường, chúng ta chỉ biết thông tin về giá cả, khối lượng giao dịch trong ngày, nhưng không biết tình trạng của thị trường chứng khoán hiện tại là gì ((thị trường bò, thị trường gấu, rung chuyển, hồi phục, v.v.), Trong trường hợp này, chúng ta có hai tập hợp trạng thái, một tập hợp trạng thái có thể quan sát được ((thị trường giá cả giao dịch, v.v.) và một tập hợp trạng thái ẩn ((thị trường chứng khoán). Chúng tôi hy vọng sẽ tìm ra một thuật toán có thể dự đoán tình trạng của thị trường chứng khoán dựa trên tình trạng giao dịch giá cả thị trường chứng khoán và giả thuyết Markov.

Trong những trường hợp trên, chuỗi trạng thái quan sát và chuỗi trạng thái ẩn có liên quan đến xác suất. Vì vậy, chúng ta có thể mô hình hóa loại quá trình này như là một quá trình Markov ẩn và một tập hợp các trạng thái có liên quan và có thể quan sát được với xác suất của quá trình Markov ẩn này, đó là mô hình Markov ẩn.

Mô hình Markov ẩn (tiếng Anh: Hidden Markov Model) là một mô hình thống kê dùng để mô tả một quá trình Markov chứa các tham số ẩn chưa biết. Vấn đề khó khăn là xác định các tham số ẩn của quá trình từ các tham số quan sát được, sau đó sử dụng các tham số này để phân tích thêm.

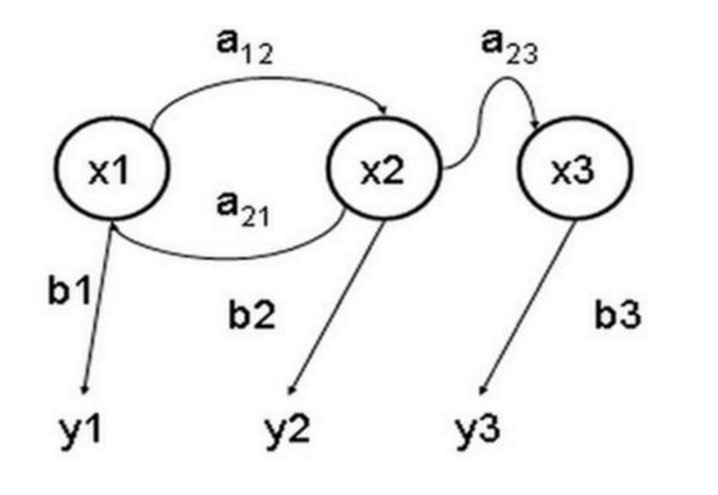
Giả sử tôi có 3 chiếc nón khác nhau trong tay. Nón đầu tiên là chiếc nón thông thường của chúng ta (gọi nó là nón D6), với 6 mặt, mỗi mặt (gọi nó là nón D4) có xác suất ¹⁄₆. Nón thứ hai là nón bốn mặt (gọi nó là nón D4) có xác suất ¹⁄₄.

Giả sử chúng ta bắt đầu với một con lắc, và chúng ta chọn một trong ba con lắc, và xác suất của mỗi con lắc là ¹⁄₃. Sau đó chúng ta chọn một con lắc, và chúng ta có một con số, 1, 2, 3, 4, 5, 6, 7, 8. Lặp lại quá trình này liên tục, chúng ta sẽ có một chuỗi các con số, mỗi con số là một trong 1, 2, 3, 4, 5, 6, 7, 8.

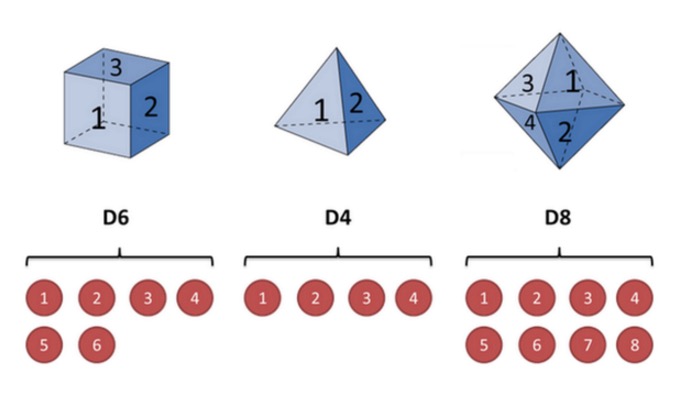
Dòng số này được gọi là chuỗi trạng thái hiển thị. Nhưng trong mô hình Markov ẩn, chúng ta không chỉ có một chuỗi trạng thái hiển thị, mà còn có một chuỗi trạng thái ẩn. Trong ví dụ này, chuỗi trạng thái ẩn là chuỗi các con lắc bạn sử dụng. Ví dụ, chuỗi trạng thái ẩn có thể là: D4 D6 D8 D6 D4 D8 D6 D6 D4

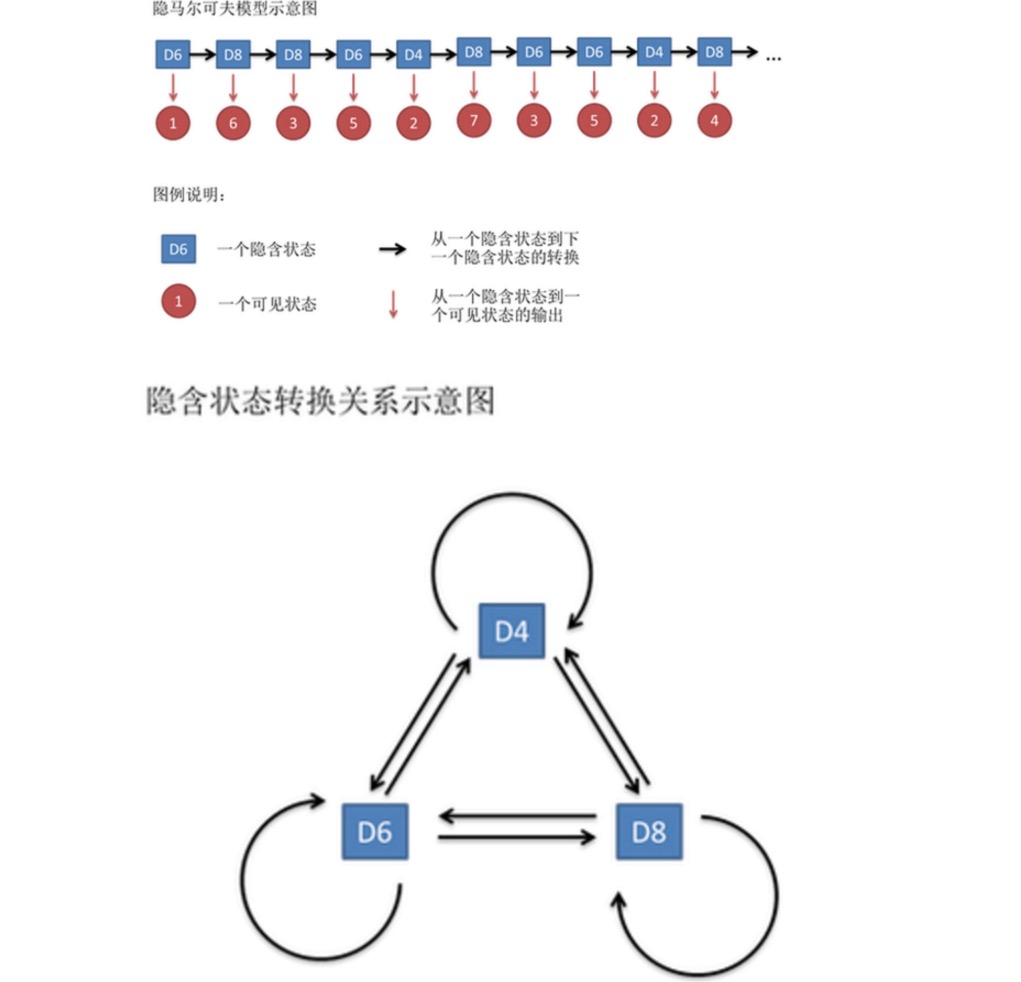
Nói chung, chuỗi Markov được nói trong HMM thực sự là chuỗi trạng thái ẩn, bởi vì giữa các trạng thái ẩn ((đỏ) có xác suất chuyển đổi. Trong ví dụ của chúng tôi, trạng thái tiếp theo của D6 là D4, D6, D8 có xác suất là 1 / 3. D4, D8, trạng thái tiếp theo của D4, D6, D8 cũng có xác suất chuyển đổi là 1/ 3.

Tương tự như vậy, mặc dù không có xác suất chuyển đổi giữa các trạng thái hiển thị, nhưng giữa các trạng thái ẩn và các trạng thái hiển thị có một xác suất được gọi là xác suất đầu ra. Trong ví dụ của chúng tôi, 6 mặt nón ((D6) tạo ra 1 có xác suất đầu ra là ¹⁄₆.

Trong thực tế, đối với HMM, nếu biết trước xác suất chuyển đổi giữa tất cả các trạng thái ẩn và xác suất đầu ra giữa tất cả các trạng thái ẩn đến tất cả các trạng thái có thể nhìn thấy, thì việc mô phỏng sẽ khá dễ dàng. Nhưng khi áp dụng mô hình HMM, thường là một phần thông tin bị thiếu, đôi khi bạn biết có bao nhiêu con bắp, mỗi con bắp là gì, nhưng không biết chuỗi con bắp được lấy ra; đôi khi bạn chỉ nhìn thấy kết quả của con bắp nhiều lần và không biết bất cứ điều gì còn lại. Nếu bạn áp dụng thuật toán để ước tính thông tin bị thiếu này, nó sẽ là một vấn đề rất quan trọng.

Các thuật toán liên quan đến mô hình HMM chủ yếu được chia thành ba loại, giải quyết ba loại vấn đề:

• Biết có bao nhiêu con cái ((số trạng thái tiềm ẩn), mỗi con cái là gì ((khả năng chuyển đổi), dựa trên kết quả của con cái ((chuỗi trạng thái có thể nhìn thấy), tôi muốn biết mỗi lần con cái nào được đưa ra ((chuỗi trạng thái tiềm ẩn)).

• Tôi cũng muốn biết có bao nhiêu con cái ((số trạng thái tiềm ẩn), mỗi con cái là gì ((khả năng chuyển đổi), và dựa trên kết quả của con cái ((chuỗi trạng thái hiển thị), tôi muốn biết xác suất của kết quả này.

• Biết được có bao nhiêu con nón ((số trạng thái ẩn), không biết mỗi con nón là gì ((khả năng chuyển đổi), quan sát được kết quả của nhiều lần nón ((chuỗi trạng thái có thể nhìn thấy), tôi muốn suy ra mỗi con nón là gì ((khả năng chuyển đổi) ‒.

  Nếu chúng ta muốn giải quyết các vấn đề trên thị trường chứng khoán, chúng ta cần giải quyết các vấn đề 1 và 3 và chúng ta sẽ xem cách thực hiện điều đó trong bài viết tiếp theo.

Tóm tắt từ bài viết không biết về Moneycode