機械学習に基づくオーダーブック高頻度取引戦略

• ### 説説

証券市場の取引機構は,オファーを駆動する市場と注文駆動する市場に分けられる.前者は,市場主として流動性を提供することに依存し,後者は,限値書状によって流動性を提供し,取引は投資家の買取委託と販売委託オップローによって形成される.中国の証券市場は,株式市場と期貨市場を含む注文駆動市場である.

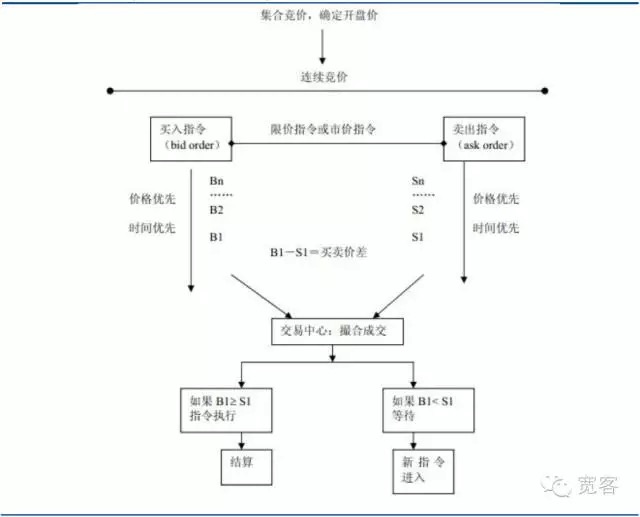図1 注文による市場図

• (一) 制限価格の注文簿の概要

  注文簿の研究は,市場マイクロ構造の研究分野に属し,市場マイクロ構造理論は,マイクロ経済学の価格理論とメーカー理論を思想源として源泉として,その核心問題である金融資産取引とその価格形成のプロセスと原因の分析において,一般均衡,局所均衡,限界利益,限界コスト,市場連続性,在庫理論,ゲーム理論,情報経済学などの複数の理論と方法を使用している.

  海外の研究の進展からすると,市場微構造の分野では,オ’ハラが代表し,大部分の理論は,在庫モデルや情報モデルなど,市場商人市場 (すなわち,オファード・ドライバ・マーケット) を行うことに基づいている.今年,実際の取引市場の中で,注文・ドライバが徐々に上位を占めているが,注文・ドライバ・マーケットを対象とした研究は比較的少ない.

  国内証券市場と期貨市場は,注文駆動市場である.下図は,株価指数期貨契約IF1312のLevel_1行情注文簿のスナップグラフである.直接上から入手する情報はあまりなく,基本的な情報は,買取価格,買取価格,買取量,販売量を含むだけである.海外のいくつかの学術論文では,注文簿と対応する情報簿もあり,最も詳細な注文集約データを含み,各注文の下落注文,成交価格,注文タイプなどの情報が含まれている.国内市場では情報簿の情報が公開されないため,超頻取引は,注文簿のみに依存できる.

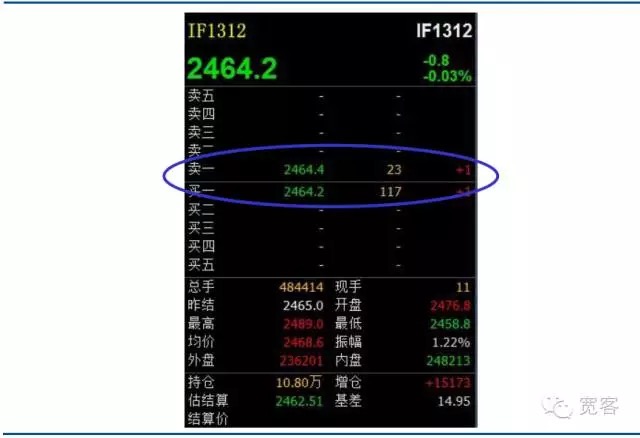  図2 株式指数期貨主力契約 レベル-1 注文簿

• (二) 注文簿の高周波取引に関する研究の進展

  注文簿の動的モデリングには,主に2つの方法がある.一つは,古典的な計量経済学方法,もう一つは,機械学習方法である.計量経済学方法は,価格差分析のMRR分解,HuangとStoll分解などの研究,注文持続期間のACDモデルの研究,価格予測のLogisticモデルの研究などの古典的な主流の研究方法である.

  機械学習は金融分野における学術研究でも非常に活発である.例えば,2012年のForecasting trends of high_frequency KOSPI200 index data using learning classifiersは,技術分析の一般的な指標 ((MA,EMA,RSIなど) を利用して市場予測を行う一般的な研究考え方である.しかし,この方法は,注文簿の動態情報への掘削が不十分である.つまり,注文簿の動態情報を使用して高値取引の研究を行う国内外の研究は比較的少ない.これは,深入研究に値する分野である.

• 2 オーダーブックの高周波取引における機械学習の応用

  • #### (a) システム構造図

  下の図は,典型的な機械学習取引戦略のシステムアーキテクチャ図であり,注文簿データ,特征発見,モデル構築と検証,取引機会のいくつかの主要なモジュールを含んでいます. 取引プロセスは,行情イベントによって引き起こされ,tick行情の到来がそのイベントの1つであることに注意してください.

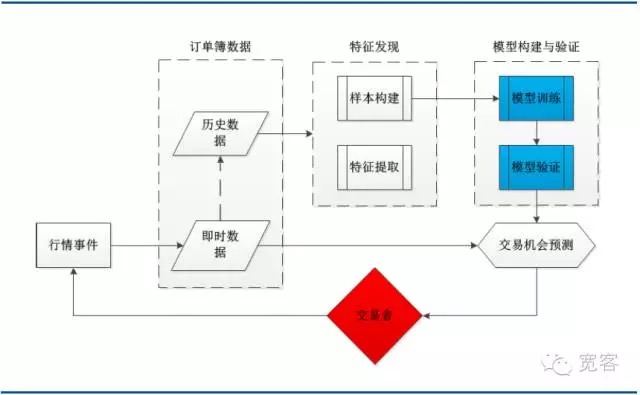  図3 機械学習に基づく注文簿モデリングのシステム構造図

  • #### (二) 支持ベクトルマシーン概要

  1970年代,ヴァプニク等人は,統計学学習理論 (SLT, Statistical Learning Theory) の比較的に完善した理論体系を構築し始め,これは,統計的規則と学習方法の性質を研究するために,限られたサンプル状況下で使用され,限られたサンプルの機械学習問題のための優れた理論的枠組みを確立し,小サンプル,非線形性,高次元,局所極小点などの実用的な問題をよりうまく解決した.1995年にヴァプニク等人が,新しい汎用学習方法 (SVM, Support Vector Machine) を明示した後,この理論は,広範な重视を受け,さまざまな分野に適用され,当初は,独自の方法よりも多くの優れたパフォーマンスを示した.

  SVMは,線形分割可能な状況における最適分類超平面から発展したものです. 2種類の分類問題に対して,トレーニングサンプルセットを ((xi,yi),i=1,2…l,lをトレーニングサンプルの数とし,xiをトレーニングサンプルとし,yiは{-1,+1}に属し,サンプルxiのクラスマーカーを入力して ((期待される出力) を求めます.

  最適な分類超平面は,すべてのサンプルを正しく分けるだけでなく,両カテゴリ間の限界を最大化することができる.限界は,訓練データセットからその分類超平面の最小距離の和として定義される. 最適な分類超平面は,テストデータに対する平均分類誤差を最小にするという意味である.

  d次元ベクトル空間に超平面がある場合:

  F(x)=w*x+b=0

  上記の2種類のデータを分離できる超平面は,分界面と呼ばれます.*x は,d次元ベクトル空間における2つのベクトルwとx の内積である.

  インタフェースは

  w*x+b=0

  この分界面を,近隣の2種類のサンプル間の距離 (Margin) を最大にする分界面は,この分界面を最適分界面と呼ぶ.

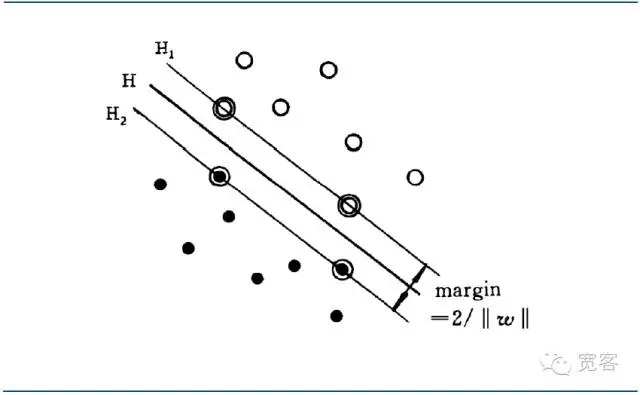  図4 SVM二分級最適分界面図

  理想的な差分界面の方程式を統一することで,2種類のサンプル間の距離を

  

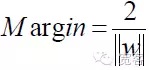
  任意のサンプルに対して,

  

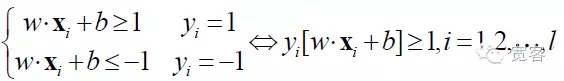
  インターフェースを最適化するには,上記の式を満たすだけでなく,最小化する必要があります.

  このSVMの問題の数学モデルは,

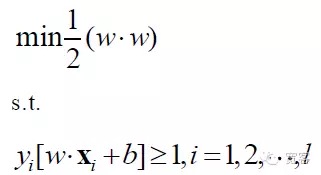
  SVMは最終的に最適化計画問題となり,学術界の研究熱点は主に迅速な解き明かし,多級,実用的な問題への応用などに焦点を当てている.

  SVMは当初,二次分類の問題に対して提唱され,現在の実用的なアプリケーションの要求に応じて,多次分類の問題に拡張された.既存の多次分類アルゴリズムは,一対多,一対一,エラー修正コード,DAG-SVMとMult i-class SVM分類器などである.

  • #### (三) 注文簿指数抽出

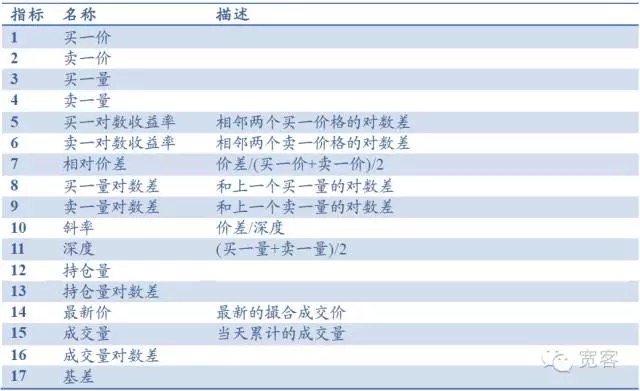
  株価指数期貨レベル-1の行情を例として,注文簿は,主に買一価,買一価,買一量,買一量などの基礎指標を含み,深さ,斜率,相対価格差などの指標を生成することができる.他の指標は,保有量,取引量,基差などを含み,合計17の指標を以下の表で示す.また,RSI,KDJMA,EMAなどの一般的な技術分析指標を導入することもできる.

  表 1 レベル行情の注文簿に基づく指標庫

  

  • #### (四) 注文簿の動的特徴図と取引機会

  市場微視の観点から,短期間の価格動力を測定する2つの方法があります.一つは中間価格動力であり,もう一つは差異交差である.本文では,よりシンプルで直観的な中間価格動力を選択します.中間価格の定義:

  

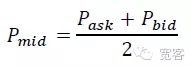
  注文簿内のΔt内の中位値ΔPの変化の大きさは,値平面の3つのカテゴリーに分かれています.

  下図は,主力契約IF1311の10月29日の中間価格動力の分布で,毎日32400のティック行情データである.

  Δt=1tickの場合,中間値の絶対値は0.2で約6000倍,絶対値は0.4で約1500倍,絶対値は0.6で約150倍,絶対値は0.8で50倍以上,絶対値は1より10倍以上変化する.

  Δt=2tickの場合,中間値の絶対値は0.2で約7000回,絶対値は0.4で約3000回,絶対値は0.6で約550回,絶対値は0.8で約205回,絶対値は1より大きい値で約10回変化する.

  変化の絶対値が0.4より大きい場合,潜在的取引機会であると考えます.Δt=1tickの場合,1日あたり約1700回の機会;Δt=2tickの場合,1日あたり約4000回の機会です.

  

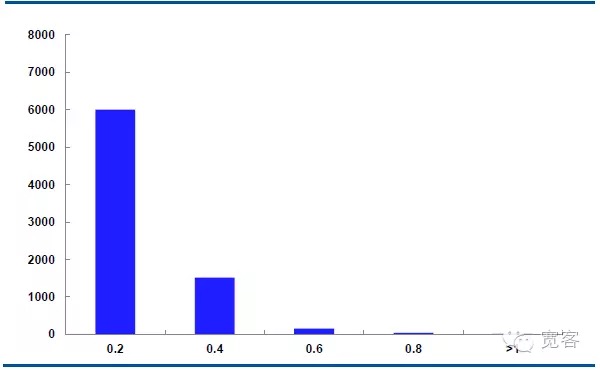
  図5 IF1311 10月29日の中間値変動分布図 ((Δt=1tick)

  

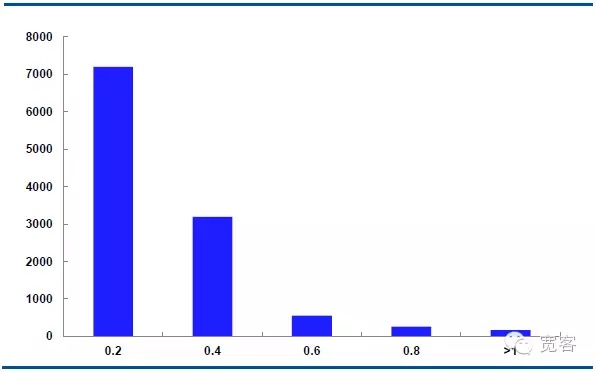
  図6 IF1311 10月29日の中間値変動分布図 ((Δt=2tick)

• 3つ目 戦略と実績

SVMモデルは大きなサンプル状況で訓練の複雑性が高く,訓練時間が長いため,IF1311の10月のLevel_1の状況データを例として,モデルの有効性を検証するために,歴史実況データの比較的短い間隔を選択しました.

• (a) モデル効果テスト

  データサイクル:IF1311契約の10月の市場データ;

  Δt値化:Δtが小さいほど,取引詳細に対する要求が高くなる.Δt=1tickの場合,実際の取引で利益を得ることは困難である.モデルの効果を比較するために,それぞれ1tick,2tick,3tickを値化する.

  モデル評価指標:サンプル精度,検査精度,予測時間. 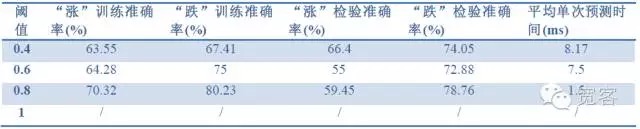表 2 1 tick データで 1 tick の効果を予測する

  表3 1 tick データで tick2 の効果を予測する

  表4 2tickデータで2tickの効果を予測する

  この3つの表のデータから,以下のような結論を導き出します. 最高の精度は約70%で,精度は60%で,取引戦略に変換できる.

• (二) 戦略模擬収益

  例えば10月31日,私たちは模擬取引を行います. 機関による株式指数期貨取引手数料は,一般的には,機関による株式指数期貨取引手数料は,一般的には,0.26/10000です.

  表5 模擬戦略 10月31日の取引状況

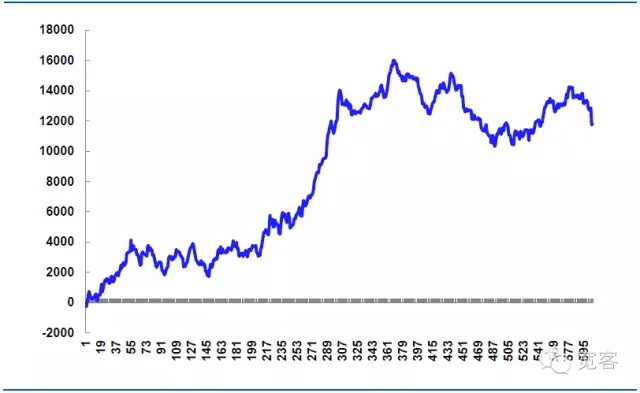
  全日605回の取引,手続を含む場合,339回の利益,勝利率56%,純利益11814.99元.

  理論上の滑走価格は14,520元であり,これは戦略実戦の鍵である.下落細部がより精密に制御された場合,滑走価格を軽減し,純利益を上げることができる.下落細部が適切に制御されていない場合,または市場の変動が異常である場合,滑走価格がより大きく,純利益は減少する.したがって,高周波取引の成功は,細部の実行に依存する.

  10月31日のアニメーション戦略の収益

記事の著作権声明: この記事の著作権は,広客公論号の作者によるものです.