কেলি সূত্র - অবস্থান নিয়ন্ত্রণের জন্য একটি শক্তিশালী হাতিয়ার

** ধরুনঃ আপনার জেতার সম্ভাবনা ৬০% এবং হারার সম্ভাবনা ৪০%। আপনার জেতার সম্ভাবনা ১০০% এবং আপনার হারার সম্ভাবনা ১০০%। অর্থাৎ, যদি আপনি জিতেন, তাহলে আপনি প্রতি ১ ডলারে ১ ডলার জিততে পারেন, যদি আপনি হেরে যান, তাহলে প্রতি ১ ডলারে ১ ডলার হারাবেন। আপনার জেতার সম্ভাবনা সীমাহীন, এবং প্রতিবারের জন্য আপনার নিজের বাজি আপনার নিজের উপর নির্ভর করে। প্রশ্নঃ ধরুন আপনার প্রাথমিক মূলধন ১০০ ডলার, তাহলে আপনি কীভাবে বাজি ধরবেন, অর্থাৎ প্রতিবারের জন্য আপনার বাজি কত শতাংশ, যাতে দীর্ঘমেয়াদী লাভ সর্বাধিক করা যায়।

• ১। এই স্ট্যাকের জন্য, প্রতিবার বাজি ধরে প্রত্যাশিত আয় হল বাজি রাখা অর্থের ৬০%*1-40%*1=20%, প্রত্যাশিত আয় পজিটিভ। অর্থাৎ, এটি একটি অস্থিরতা যেখানে হ্যাকাররা জয়লাভ করে, এবং তাদের একটি বিশাল সুবিধা রয়েছে।

আমরা কিসের উপর বাজি ধরব?

যদি আমরা কঠোরভাবে চিন্তা না করি, তাহলে আমরা ভাবতে পারি যে, যদি আমি প্রতিবার ২০% আয় আশা করি, তাহলে দীর্ঘমেয়াদী সর্বাধিক লাভ অর্জনের জন্য, আমি প্রতিবারই মূলধনের যতটা সম্ভব একটি অংশ রাখতে চেষ্টা করব। এই অনুপাতের সর্বোচ্চ মান হল ১০০%।

কিন্তু স্পষ্টতই, প্রতিটি বাজিতে ১০০% মূলধন রাখা অযৌক্তিক, কারণ একবার বাজি বাজি হেরে গেলে, সমস্ত মূলধন হারাবে, আর পরের রাউন্ডে অংশ নিতে পারবে না, কেবল শান্তভাবে চলে যাবে। দীর্ঘমেয়াদে, একবার বাজি হারালে এই ঘটনাটি অবশ্যই ঘটবে, তাই দীর্ঘমেয়াদে অবশ্যই দেউলিয়া হবে।

সুতরাং এখানে একটি উপসংহারে আসে যে, যতক্ষণ না একটি স্থগিতাদেশের সম্ভাবনা থাকে যে মূলধনটি একসাথে হারিয়ে যাবে, এমনকি যদি এটি খুব ছোট হয়, তবে এটি কখনই পূর্ণ হবে না। কারণ দীর্ঘমেয়াদে, ছোট সম্ভাব্যতার ঘটনাগুলি অবশ্যই ঘটবে, এবং বাস্তব জীবনে, ছোট সম্ভাব্যতার ঘটনার প্রকৃত সম্ভাব্যতা তার তাত্ত্বিক সম্ভাব্যতার চেয়ে অনেক বড়। এটিই ফিনান্সিংয়ের ঘন ঘন প্রভাব।

• ২। অবরুদ্ধ অবস্থার দিকে ফিরে যাওয়া ১। যেহেতু প্রতিবার ১০০% বাজি দেওয়া অযৌক্তিক, তাহলে ৯৯% কি হবে? যদি প্রতিবার ৯৯% বাজি দেওয়া হয়, তাহলে আপনি কখনই দেউলিয়া হবেন না, এবং যদি আপনি ভাগ্যবান হন তবে আপনি সম্ভবত অনেক লাভ করতে পারবেন।

কিন্তু এই ঘটনাটি কি সত্যি?

আমরা এই সমস্যাটি তত্ত্বগতভাবে বিশ্লেষণ করি না, আমরা একটি পরীক্ষা করতে পারি। আমরা এই অচলাবস্থাকে অনুকরণ করি এবং প্রতিবার ৯৯% বাজি ধরে দেখি ফলাফল কী হবে।

এই সিমুলেশনটি খুবই সহজ, এটি এক্সেল দিয়ে করা যায়। নিচের চিত্রটি দেখুনঃ

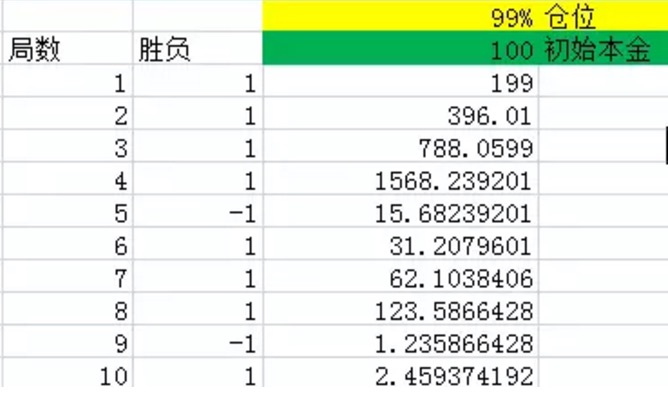চিত্র ১

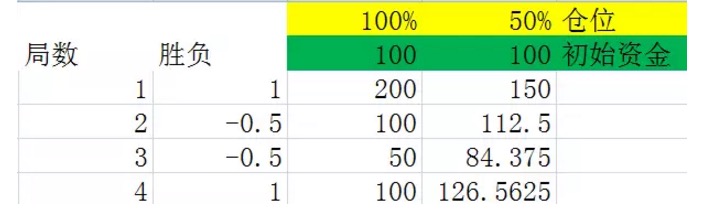
উপরের চিত্রের মতো, প্রথম কলামটি রানের সংখ্যাকে নির্দেশ করে। দ্বিতীয় কলামটি বিজয়ী, এক্সেল 60% সম্ভাবনা অনুসারে 1 উত্পন্ন করবে, অর্থাৎ 60% সম্ভাবনা নেট রিটার্ন 1,40% সম্ভাবনা -1 উত্পন্ন করবে, অর্থাৎ 40% সম্ভাবনা নেট রিটার্ন -1। তৃতীয় কলামটি প্রতিটি রানের শেষে সমস্ত তহবিলকে জ্যাক করে। এই পরীক্ষার প্রতিটি পজিশনে 99%, প্রাথমিক মূলধন 100 হয়, যা হলুদ এবং সবুজ দ্বারা চিহ্নিত।

ছবি থেকে দেখা যাচ্ছে যে, ১০টি রাউন্ডের পর, ১০টি রাউন্ডের মধ্যে ৮টি রাউন্ড জিতেছে, যা ৬০% এর চেয়ে বেশি, মাত্র দু’বার হেরেছে। কিন্তু তা সত্ত্বেও, শেষের দিকে ২.৪৬ ইউয়ান বাকি ছিল, যা মূলত ক্ষতি।

এবং যখন আমি এই সংখ্যাকে বাড়িয়ে দিই, 1,000, 2,000, 3,000… এবং আপনি দেখতে পাচ্ছেন, শেষ অবধি, আমাদের হাতে থাকা অর্থের পরিমাণ প্রায়শই শূন্যে চলে যায়।

যদি আমরা ৯৯% না করি, তাহলে আমরা অন্য কিছু অনুপাতের সাথে চেষ্টা করব, নিচের চিত্রটি দেখুনঃ এই চিত্র থেকে দেখা যায় যে, যখন পজিশন ধীরে ধীরে কমিয়ে ৯৯% থেকে ৯০%, ৮০, ৭০, ৬০% করা হয়, তখন একই ১০ রাউন্ডের ফলাফল সম্পূর্ণ ভিন্ন হয়। এই চিত্র থেকে দেখা যায় যে, পজিশন ধীরে ধীরে ছোট হওয়ার সাথে সাথে ১০ রাউন্ডের পর তহবিল ধীরে ধীরে বড় হয়।

এখানে, আপনি দেখতে পাবেন যে এই সমস্যাটি এত সহজ নয়। এমনকি যদি এটি একটি বড় সমস্যা হয়, তবে এটি এমন একটি সমস্যা নয় যে আপনি যে কোনও সময় জিততে পারবেন না।

তাই, দীর্ঘমেয়াদে সর্বোচ্চ লাভ অর্জনের জন্য কি করা উচিত?

যদি আপনি একটি ছোট স্কেল ব্যবহার করেন, তাহলে আপনি কি মনে করেন যে, আপনি যদি একটি ছোট স্কেল ব্যবহার করেন, তাহলে আপনি লাভবান হবেন? না, কারণ স্কেলটি শূন্য হয়ে গেলে, আপনি স্পষ্টভাবে অর্থ উপার্জন করতে পারবেন না।

তাই, এই অনুপাতটি ঠিক কত?

এই প্রশ্নের উত্তর দিতে বিখ্যাত ক্যালি সূত্র ব্যবহার করা হয়!

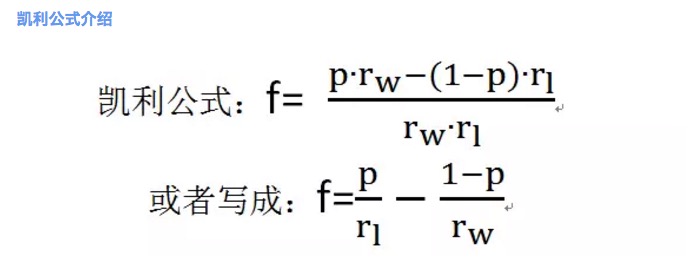চিত্র ২

যেখানে f হল সর্বোত্তম বাজির অনুপাত; p হল জয়ের সম্ভাবনা; rw হল জয়ের সময় নিট লাভের হার, যেমন, স্ট্যাক 1 তে rw = 1; rl হ’ল হারানোর সময় নিট ক্ষতির হার, যেমন, স্ট্যাক 1 তে rl = 1; নোট করুন যে rl> 0।

ক্যালি সূত্র অনুসারে, স্ট্যাক 1 এ সর্বাধিক বাজির হার 20% হিসাবে গণনা করা যায়।

আমরা একটি পরীক্ষা চালাতে পারি, যাতে আমরা এই সিদ্ধান্তটি আরও ভালভাবে বুঝতে পারি।

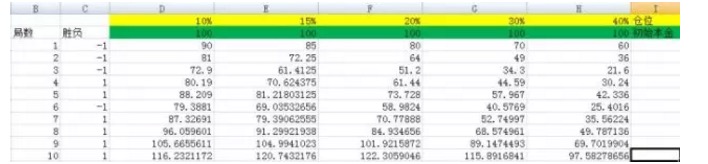চিত্র ৩

চিত্রের মতো, আমরা পজিশনগুলি যথাক্রমে 10%, 15%, 20%, 30%, 40% হিসাবে সেট করেছি। তাদের সংশ্লিষ্ট কলামগুলি যথাক্রমে ডি, ই, এফ, জি এবং এইচ।

এবং যখন আমি ৩,০০০ বার পরীক্ষাটি করেছি, এবং যখন আমি ৫,০০০ বার পরীক্ষাটি করেছি, আপনি দেখতে পারেন যে F-এর ফলনটি সবচেয়ে বড়, এবং অন্যান্য কলামের তুলনায় চাপের মূলটি একটি পরিমাণের পরিমাণ নয়। এবং F-এর পজিশনের অনুপাতটি 20%।

ক্যালি সূত্রের শক্তি দেখুন ৷ উপরের পরীক্ষায়, যদি আপনি দুর্ভাগ্যবশত অনুপাতটি ৪০% বেছে নেন, অর্থাৎ H কলামে, তাহলে ৫,০০০ রান বাজি ধরে আপনার মূলধন ১০০ থেকে ২২৭৯৯৯৮৫.৭৫ হয়ে যায়, যদিও লাভ অনেক বেশি ৷ কিন্তু ২০% অনুপাতের ফলাফলের সাথে তুলনা করলে, এটা অর্থহীন ৷

এটা জ্ঞানের শক্তি!

• ৩। ক্যালি সূত্র বোঝা

ক্যালি সূত্রের গাণিতিক উপসংহার এবং এর জটিলতা সম্পর্কে এখানে আলোচনা করার কোন কারণ নেই। এখানে আমি কিছু পরীক্ষার মাধ্যমে ক্যালি সূত্রের বিষয়গত বোঝার গভীরতা বাড়িয়ে তুলব।

আমরা আবার একটি বাজি দেখি। বাজি ২ঃ আপনার হারার এবং জয়ের সম্ভাবনা যথাক্রমে ৫০%। উদাহরণস্বরূপ, একটি মুদ্রা ছুড়ে ফেলা। জয়ের ক্ষেত্রে নেট রিটার্ন হার ১, অর্থাৎ rw = ১, এবং হারার ক্ষেত্রে নেট ক্ষতির হার ০.৫, অর্থাৎ rl = ০.৫। অর্থাৎ, যখন আপনি প্রতি এক ডলার জিতবেন, জয়ের সময় আপনি আরও এক ডলার জিতবেন, এবং হারানোর সময় আপনি কেবল ৫ সেন খরচ করবেন।

এটি সহজেই বোঝা যায় যে স্ট্যান্ডবাই ২ এর প্রত্যাশিত আয় ছিল ০.২৫, এবং এটি একটি স্ট্যান্ডবাই যেখানে হ্যাকারদের একটি বিশাল সুবিধা রয়েছে।

ক্যালি সূত্র অনুসারে, আমরা প্রতি দশে সর্বোত্তম বাজির অনুপাত পেতে পারিঃ

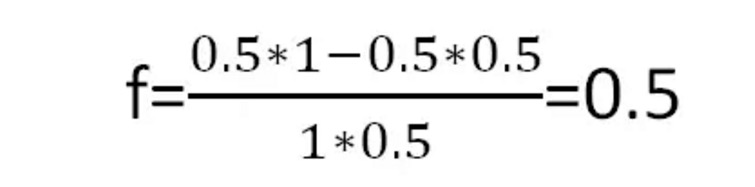চিত্র ৪

অর্থাৎ, প্রতিবার অর্ধেক টাকা নিয়ে বাজি ধরলে, দীর্ঘমেয়াদে সবচেয়ে বেশি লাভ পাওয়া যায়।

এখানে আমি পরীক্ষার মাধ্যমে গড় বৃদ্ধির হার r এর ধারণার কথা বলব।

প্রথমত, ২.১ পরীক্ষার দুটি চিত্র দেখুনঃ

চিত্র ৫

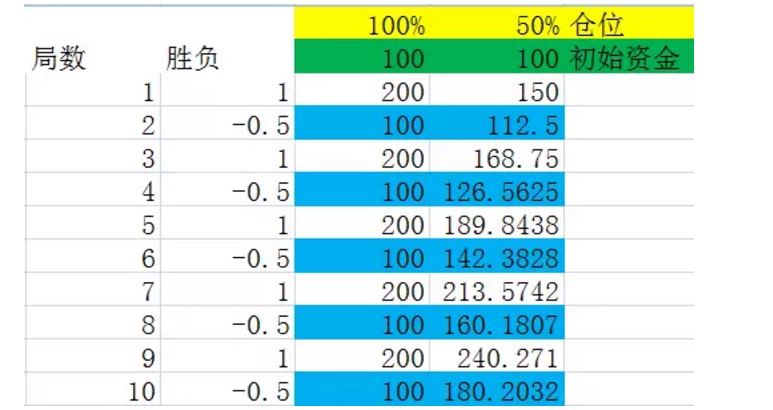
এই দুটি চিত্র হল মডেলিং স্ট্যাকডাউন ২ এর পরীক্ষা, দ্বিতীয় কলামের জয়ের এবং নেতিবাচক কলামে, পরীক্ষার 50% সম্ভাবনা রয়েছে 1 লাভ 100%; 50% সম্ভাবনা রয়েছে -0.5; ক্ষতি 50%; তৃতীয় এবং চতুর্থ কলামটি হ’ল পজিশনের 100% এবং 50% প্রতিটি স্ট্যাকডাউনের পরে মালিকানাধীন তহবিল।

এই দুইটি অঙ্কনকে সাবধানে তুলনা করলে দেখা যায় যে, একই সংখ্যক অঙ্কন অতিক্রম করার পর, চূড়ান্ত ফলাফলটি কেবলমাত্র এই অঙ্কনগুলিতে জিতে যাওয়া অঙ্কন এবং হারানো অঙ্কনের সংখ্যার সাথে সম্পর্কিত, এবং এই অঙ্কনগুলিতে জিতে যাওয়া অঙ্কন এবং হারানো অঙ্কনের ক্রমের সাথে সম্পর্কিত নয়। উদাহরণস্বরূপ, পূর্ববর্তী দুটি অঙ্কনে একইভাবে 4 টি অঙ্কন করা হয়েছে, একইভাবে প্রতিটি অঙ্কনে দুটি জয় এবং দুটি পরাজয় রয়েছে, তবে প্রথম অঙ্কনের হারানো ক্রমটি জয়-পরাজয়, দ্বিতীয় অঙ্কনের হারানো-পরাজয়-পরাজয়। তাদের চূড়ান্ত ফলাফল একই।

অবশ্যই এই সিদ্ধান্তটি খুব সহজেই প্রমাণ করা যায় (প্রজনন বিনিময় আইন, প্রাথমিক বিদ্যালয়ের শিক্ষার্থীরা এটি করতে পারে), এখানে এটি প্রমাণিত হয় না, উপরের দুটি উদাহরণ যথেষ্ট ভালভাবে বোঝার জন্য যথেষ্ট।

সুতরাং, যেহেতু চূড়ান্ত ফলাফলের সাথে জয়-পরাজয়ের কোন সম্পর্ক নেই, তাই আমরা ধরে নিই যে স্ট্যাকডাউন ২ পরীক্ষা ২.২-এর মতই চলবে, নিচের চিত্রটি দেখুনঃ

চিত্র ৬

আমরা ধরে নিই যে জয়ের পর জয়ের পাল্টা পাল্টা হয়, কারণ উপসংহার এক, দীর্ঘমেয়াদে এই অর্থের কোনও প্রভাব নেই।

ছবিটি দেখার আগে, আমরা একটি সংজ্ঞা তৈরি করি। ধরুন, আমরা কিছু স্ট্যান্ডবাইকে একটি সমষ্টি হিসাবে বিবেচনা করি, যেখানে বিভিন্ন ফলাফলের ফ্রিকোয়েন্সি তার সম্ভাবনার সমান, এবং এই সমষ্টির স্ট্যান্ডবাই সংখ্যাটি সমস্ত শর্তযুক্ত সমষ্টির মধ্যে সর্বনিম্ন স্ট্যান্ডবাই সংখ্যা। উদাহরণস্বরূপ, উপরের চিত্রের পরীক্ষায়, স্ট্যান্ডবাইয়ের একটি সেট দুটি স্ট্যান্ডবাইয়ের প্রতিনিধিত্ব করে, যার মধ্যে একটি জিতেছে এবং একটি হেরেছে।

উপরের চিত্রের নীল চিহ্নিত সংখ্যার দিকে ঘনিষ্ঠভাবে নজর দিন, এগুলি একটি স্থিরতার সমাপ্তি। আপনি দেখতে পাবেন যে এই সংখ্যাগুলি ধারাবাহিকভাবে বৃদ্ধি পেয়েছে। যখন পজিশনটি 100% ছিল, তখন নীল চিহ্নিত সংখ্যার বৃদ্ধির হার ছিল 0%, অর্থাত্ স্থিরতার পরে মূলধনের বৃদ্ধি ছিল 0%। এটি ব্যাখ্যা করে যে যখন প্রতিটি পজিশন পূর্ণ ছিল, তখন পজিশন 2 দীর্ঘমেয়াদে অর্থ উপার্জন করতে পারে না। যখন পজিশনটি 50% ছিল (অর্থাৎ ক্যালি সূত্র থেকে প্রাপ্ত সর্বোত্তম অনুপাত), তখন নীল চিহ্নিত সংখ্যার বৃদ্ধির হার ছিল 12.5%, অর্থাত্ স্থিরতার পরে মূলধনের বৃদ্ধি ছিল 12.5%।

এটি একটি সাধারণ নিয়ম যে প্রতিটি স্ট্যান্ডার্ডের পরে বৃদ্ধির হার পজিশনের সাথে সম্পর্কিত। এবং প্রতিটি স্ট্যান্ডার্ডের পরে বৃদ্ধির হার যত বেশি, দীর্ঘমেয়াদে চূড়ান্ত লাভ তত বেশি।

প্রতিটি স্ট্যান্ডার্ডের বৃদ্ধির হার থেকে প্রতিটি স্ট্যান্ডার্ডের গড় বৃদ্ধির হার গণনা করা যেতে পারে g. উপরের চিত্রটিতে, যদি প্রতিটি স্ট্যান্ডার্ডের মধ্যে দুটি স্ট্যান্ডার্ড থাকে, তবে প্রতিটি স্ট্যান্ডার্ডের গড় বৃদ্ধির হার

চিত্র ৭

দীর্ঘমেয়াদে, মূলধন সর্বাধিক বৃদ্ধি পেতে চাইলে, কেবলমাত্র r সর্বাধিক করুন, অর্থাৎ g সর্বাধিক করুন। এবং সর্বোত্তম বাজি অনুপাত f আসলে max ((g) এর সমাধানের মাধ্যমে আসে।

• ৪। ক্যালি সূত্রের অন্যান্য উপসংহার

কেলি কিংবদন্তি

ক্যালি সূত্রটি প্রথমে এটিএন্ডটি বেল ল্যাবরেটরিজ পদার্থবিদ জন ল্যারি ক্যালিকে তার সহকর্মী ক্লাউড এলউড শেনন এর দীর্ঘ দূরত্বের টেলিফোন লাইন গুজব গবেষণার উপর ভিত্তি করে তৈরি করেছিলেন। ক্যালি শেনন এর তথ্য তত্ত্বকে কীভাবে একটি জুয়াড়িকে তার ইন-লাইন বার্তাগুলির সাথে জুয়া খেলার সময় প্রয়োগ করতে হবে তা সমাধান করেছেন। জুয়াড়ি সর্বোত্তম বাজি পরিমাণ নির্ধারণ করতে চায়, এবং তার ইন-লাইন বার্তাগুলি নিখুঁত হওয়া উচিত নয়, যা তাকে একটি দরকারী সুবিধা দেয়। ক্যালি এর সূত্রটি পরবর্তীকালে শেননের অন্য সহকর্মী এডওয়ার্ড সোপ দ্বারা একুশ পয়েন্ট এবং শেয়ার বাজারে প্রয়োগ করা হয়েছিল। সোপ তার কাজের অবকাশ ব্যবহার করে, কয়েক মাসের কঠোর গণনার মাধ্যমে, একটি গাণিতিক প্রবন্ধ লিখেছিলেন, যার শিরোনাম ছিল “২১ পয়েন্ট বাজি পছন্দসই কৌশল”। তিনি তার জ্ঞান ব্যবহার করে, রাতারাতি বাজি নেভাদারানো শহরের সমস্ত ক্যাসিনো আক্রমণ করেছিলেন এবং সফলভাবে ২১ পয়েন্ট বাজি টেবিল থেকে কয়েক হাজার ডলার জিতেছিলেন। তিনি মার্কিন যুক্তরাষ্ট্রের ওয়াল স্ট্রিট কোয়ান্টাম ট্রেডিং হেজ ফান্ডের আদিপিতা ছিলেন, যিনি 1970 এর দশকে প্রথম কোয়ান্টাম ট্রেডিং হেজ ফান্ড তৈরি করেছিলেন। 1962 সালে প্রকাশিত তাঁর কলামটি জুয়া খেলোয়াড়কে পরাজিত করে, যা অর্থনীতির অন্যতম ক্লাসিক বই হয়ে ওঠে।

দৃষ্টিভঙ্গির ব্যবহার

ক্যালি ফর্মুলা কিভাবে বাস্তব জীবনে অর্থ উপার্জন করতে পারে? ক্যালি ফর্মুলার ব্যবহারের শর্ত পূরণ করে এমন একটি অচলাবস্থা তৈরি করা। আমার মতে, এই অচলাবস্থা অবশ্যই আর্থিক বাজার থেকে এসেছে। সম্প্রতি আমি ট্রেডিং সিস্টেম নিয়ে গবেষণা করছি, একটি ভালো ট্রেডিং সিস্টেমের জন্য সবচেয়ে গুরুত্বপূর্ণ কি? একটি প্রত্যাশিত লাভের জন্য ইতিবাচক ক্রয়-বিক্রয় নিয়মের গুরুত্ব ১০% এবং একটি ভাল তহবিল নিয়ন্ত্রণ পদ্ধতির গুরুত্ব ৪০% এবং বাকি ৫০% মানুষের মানসিক নিয়ন্ত্রণের উপর নির্ভর করে। ক্যালি সূত্রের সাহায্যে আমি আমার পজিশন নিয়ন্ত্রণ করতে পারি। উদাহরণস্বরূপ, আমি আগে একটি স্টক ট্রেডিং সিস্টেম গবেষণা করেছি, যা প্রতি সপ্তাহে একটি ট্রেড করে, প্রতি সপ্তাহে ট্রেডিং সাফল্যের সম্ভাবনা 0.8 এবং ব্যর্থতার সম্ভাবনা 0.2। যখন সফল হয় তখন 3% উপার্জন করা যায় ((কমিশন, মুদ্রা ট্যাক্স ছাড়িয়ে) এবং প্রতি ব্যর্থতার ক্ষতি 5%। ক্যালি সূত্রটি না জানার আগে, আমি অন্ধভাবে পূর্ণ পজিশন ট্রেডিং করছিলাম এবং আমার অবস্থানটি ঠিক ছিল না তা জানতাম না। ক্যালি সূত্রটি ব্যবহার করার পরে, গণনা করা সর্বোত্তম অবস্থানটি 9.33 হওয়া উচিত, অর্থাৎ যদি ঋণের সুদের হার 0 হয় তবে দ্রুততম তহবিল বৃদ্ধির গতি পেতে চাইলে লিভারেজ ট্রেডিং ব্যবহার করতে হবে, সূত্রটি গণনা করে প্রতি ট্রেডের গড় বৃদ্ধির হার r প্রায় 7.44% এবং পূর্ণ পজিশনের ব্যবসায়ের গড় তহবিল বৃদ্ধির হার প্রায় r 1.35 হয় ((এটি প্রকৃত প্রত্যাশিত আয়) । পরীক্ষার পরে, আমি মডেলিংয়ের মাধ্যমে জানতে পেরেছি যে লিভারেজ ট্রেডিং ব্যবসায়ের তুলনায় লিভারেজ ট্রেডিং ট্রেডিংয়ের গতি আরও ভাল ক্যালি সূত্রটি বাস্তবে এতটা সহজ হতে পারে না, এবং অনেকগুলি অসুবিধা রয়েছে যা অতিক্রম করতে হবে। উদাহরণস্বরূপ, লিভারেজ এক্সচেঞ্জের জন্য প্রয়োজনীয় তহবিলের ব্যয়, উদাহরণস্বরূপ, বাস্তবে তহবিল সীমাহীনভাবে ভাগযোগ্য নয়, উদাহরণস্বরূপ, আর্থিক বাজারে এটি এতটা সহজ নয় যেমন উপরে উল্লিখিত সহজ স্থবিরতা। কিন্তু যাই হোক না কেন, ক্যালি ফর্মুলা আমাদের সামনে এগিয়ে যাওয়ার পথ দেখায়।