Curtosis y asimetría

• #### Pico (kurtosis) y inclinación (skewness)

Publicado por EasyTrader

Esta es una estrategia de negociación aplicada por la curtosis y la skewness distribuidas por estadísticas. Cuando la información es tendencia y la tendencia potencial es positiva, hacemos más. Cuando la información es tendencia y la tendencia potencial es negativa, hacemos un descuento.

Entonces, ¿cómo podemos determinar la tendencia y la intensidad de la tendencia?

Primero, veamos la definición de una distribución normal.

Distribución (distribution): distribución en la que todos los valores de las variables aparecen en la misma frecuencia, con el eje horizontal como el valor de la variable y el eje vertical como la frecuencia de aparición. Distribución normal: también conocida como distribución de Gaussian

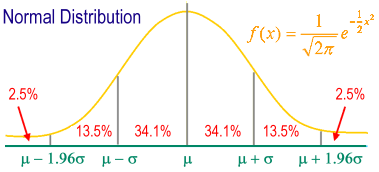
Distribución normal estándar: gráfico de distribución normal centrado en la media y con la desviación estándar como la unidad básica del eje del reloj.

m ± 1s contiene el 68.26% de los individuos de toda la muestra.

m ± 2s contiene el 95.44% de los individuos de toda la muestra.

m ± 3s contiene el 99,74% de los individuos de toda la muestra.

El 95% de los individuos cae entre m ± 1.96s.

El 99% de los individuos cae entre m ± 2.58s.

En estadística, la pico (Kurtosis) mide el estado pico de la distribución de probabilidades de una variable aleatoria real. Un pico alto significa que el aumento de la diferencia es causado por un extremo de diferencia mayor o menor que el promedio de la baja frecuencia.

El pico (curtosis) es una medida estadística de la intensidad de la curvatura de la distribución de un conjunto de datos. El pico de la distribución normal es 3, por lo que llamamos picos a los picos mayores de 3, lo que significa que la distribución de los datos es más concentrada y uniforme que la distribución normal.

La skewness representa la simetría de la distribución de datos, o la posición de un número en un dato. La skewness es igual a 0 y representa la simetría perfecta. Esta estadística también se compara con la distribución normal: la skewness mayor que 0 indica que, en comparación con la distribución normal, la matriz presenta un desplazamiento a la derecha, representado como la cola larga de la derecha y con los valores extremos más dispuestos a la derecha; por el contrario, la skewness a la izquierda, representada como la cola larga de la izquierda y con los valores extremos más dispuestos a la izquierda.

En la teoría de la probabilidad y la estadística, la desviación mide la asimetría de la distribución de probabilidades de variables aleatorias reales. Los valores de desviación pueden ser positivos, negativos o incluso no definibles. En términos cuantitativos, una desviación negativa significa que el extremo izquierdo de la función de densidad de probabilidad es más largo que el extremo derecho y que la mayoría de los valores (incluyendo el promedio) están a la derecha del promedio.

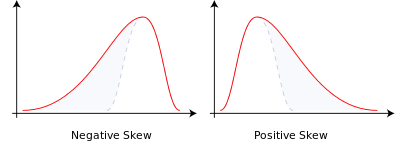
La tendencia es de dos tipos:

• Paresia negativa o paresia izquierda: la cola de la izquierda es más larga y el cuerpo principal de la distribución se concentra en la derecha.
• Positivo parásito o parásito derecho: la cola es más larga en el lado derecho y el cuerpo principal de la distribución se concentra en el lado izquierdo.
• Si la distribución es simétrica, entonces el promedio es igual al promedio y la desviación es cero (además, si la distribución es una distribución de un solo pico, entonces el promedio es igual al promedio y el promedio es igual al número entero).

• Por lo tanto, se obtienen las siguientes reglas de transacción: Cuando el pico es menor que 0 (el mercado está en un mercado de tendencia), la oscilación es mayor que N (la tendencia es al alza), hacer más; Cuando el pico es menor que 0 (el mercado está en tendencia), la desviación es menor que M (la tendencia es a la baja), el shorting;

MATLAB: Los interesados pueden convertirlo a un lenguaje de prueba en JS.

input:ExitType(5) ;
input:NBarL(2),NBarS(2),TradeProfit(0.053),TradeStopLoss(0.023),ATRs_L(5.4),ATRs_S(10.9);
vars: IsBalanceDay(False),MP(0),PF(0),PL(0),HLRange(100);

inputs:Length(20),Trigger(3),UpSkew(3.4),DownSkew(2.2) ;
vars:KurtValue(0),SkewValue(0),BuyPoint(0),SellPoint(0);

MP = MarketPosition ;
if DAYofMonth(Date) > 14 and DAYofMonth(Date) < 22 and DAYofWeek(Date)= 3 then isBalanceDay = True else isBalanceDay =False ;

PF = AvgPrice*TradeProfit ;
PL = AvgPrice*TradeStopLoss ;

{计算峰度 }
KurtValue = Kurtosis(Close,Length) ;
{计算偏度}
SkewValue = Skew(Close,Length) ;

{ 峰度向下跌破 Trigger 线 ,建立买卖点 }
if KurtValue Cross under Trigger then Begin
BuyPoint = High 3;
SellPoint = Low-3;
end;

{ 偏度大于某数值后 ,趋势确认进场作多 }
if  SkewValue > -UpSkew 2 then Buy next bar at BuyPoint stop ;
{ 偏度小于某数值后 ,趋势确认进场作空 }
if  SkewValue < -DownSkew 2 then Sell next bar at SellPoint Stop ;
end;

if ExitType = 1 then SetStopLoss(PL * BigPointValue) ;

if ExitType = 2 then Begin
SetStopLoss(PL * BigPointValue) ;
setProfitTarget(PF * BigPointValue) ;
end;

if ExitType = 3 then Begin
if MP > 0 and BarsSinceEntry = NBarL then ExitLong next bar at Market ;
if MP < 0 and BarsSinceEntry = NBarS then ExitShort next bar at Market ;
end;

if ExitType = 4 then Begin
SetStopLoss(PL * BigPointValue) ;
setProfitTarget(PF * BigPointValue) ;
if MP > 0 and BarsSinceEntry = NBarL then {Sell } ExitLong next bar at Market ;
if MP < 0 and BarsSinceEntry = NBarS then {Buy} ExitShort next bar at Market ;
end;

if ExitType = 5 then Begin
{*******************************************************************
Description : ATR Trailing Stop Long Exit
Provided By : Omega Research, Inc. (c) Copyright 1999
********************************************************************}
{Inputs: ATRs_L(3);}
Variables: PosHigh(0), ATRVal_L(0);

ATRVal_L = AvgTrueRange(10) * ATRs_L;
If BarsSinceEntry = 0 Then PosHigh = High;
If MarketPosition = 1 Then Begin
If High > PosHigh Then PosHigh = High;
ExitLong ("ATR") Next Bar at PosHigh - ATRVal_L Stop;
End else ExitLong ("ATR eb") Next bar at High - ATRVal_L Stop;

{*******************************************************************
Description : ATR Trailing Stop Short Exit
Provided By : Omega Research, Inc. (c) Copyright 1999
******************************************************************}
{Inputs: ATRs_S(3);}
Variables: PosLow(0), ATRVal_S(0);

ATRVal_S = AvgTrueRange(10) * ATRs_S;
If BarsSinceEntry = 0 Then PosLow = Low;
If MarketPosition = -1 Then Begin
If Low < PosLow Then PosLow = Low;
ExitShort ("ATR_1") Next Bar at PosLow ATRVal_S Stop;
End else ExitShort ("ATR_1 eb") Next bar at Low ATRVal_S Stop;
end;

if IsBalanceDay then setExitonClose ;

Reproducido desde el blog de Faruto