ケリーの公式 - 位置制御のための強力なツール

---

** 賭け場1:あなたの勝つ確率は60%で,負ける確率は40%である.勝ったときの純利益率は100%,負けたときの負ける確率は100%である.つまり,勝った場合,あなたは1ドルにつき1ドルを獲得し,負けた場合,1ドルにつき1ドルを失う.賭け場は無限回,毎回の下注はあなた自身の任意の設定によって行われる.

• 1 賭けの利回りは,賭け金額の60%です.*1-40%*1=20%,期待収益は正である。つまり,これは客が優勢で,非常に大きな優勢を持つ局である。

ギャンブルを賭けるにはどうすればいいのでしょうか?

厳密に考えずに,粗略に想像してみると,私の賭博毎の予想収益が20%なので,長期的に最大利益を達成するために,私は賭博毎に本金の一定の割合をできるだけ多く置くべきです.この割合の最大値は100%です.

しかし,明らかに,賭博の各局に100%の本金を置くことは不合理である.なぜなら,賭博の1局が負けたら,すべての本金がすべて失われ,次の局には参加できず,静かに退場するしかないからです.そして,長期的には,賭博の1局が負けた場合,このイベントは必ず起こるので,長期的には必ず破産します.

だから結論はこうです. ギャンブルが起こる限り,一瞬で本金全額を失う可能性は,たとえ非常に小さな可能性であっても,決して満席にはならない. 長期的に見ると,小確率の事件は必然的に起こるのであり,現実生活において,小確率の事件の発生の実際の確率は,その理論的確率がはるかに大きい.これが金融学の肥尾効果である.

• 2 停滞点に戻る 毎回100%の賭けは不合理なので,99%はどうでしょう.毎回99%の賭けは,決して破産しないという保証だけでなく,運が良ければ,大きな利益も得られます.

イスラム教は,イスラム教が,イスラム教が,イスラム教が,イスラム教が,イスラム教が,

理論的に分析するのではなく,実験的にやってみましょう. 賭け場を模擬して,毎回99%を賭けて,結果がどうなるか見てみましょう.

このシミュレーションはExcelで簡単にできます. 下の図を見てください.

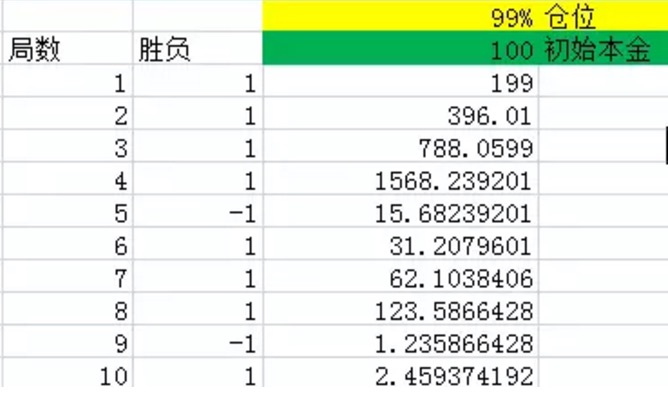グラフ1

上図のように,第1列は局数を表している。第2列は勝負であり,excelは60%の確率で1を発生させる,すなわち60%の確率で純利益率を1,40%の確率で−1を発生させる。第3列は,各局の終了時に全ての資金を客とする。この実験では,各回の賭けポジションは99%,初期資本は100であり,黄色と緑で示されている。

図からわかるように,10回をかけて10回を8回で勝って,60%の確率より大きく,たった2回だけ負けてしまった。しかし,そうであっても,最後の資金は2.46元しか残らず,基本的には負けてしまった。

実験を1000回,2000回,3000回まで増やすと 予想通り 資金は基本的に0になるのです

99%もダメなので,他の数値でやってみよう. 図からわかるように,ポジションを徐々に99%から90%,80%,70%,60%に減らすと,同じ10局の結果は全く違う.図からわかるように,ポジションが徐々に小さくなると,10局後の資金は徐々に大きくなっている.

ギャンブルがこれほど大きなギャンブルであっても,ギャンブルを勝てるのは,ただ単にギャンブルを勝てるだけではありません.

長期的に見れば 利益の最大化のために 賭けるべきことは何でしょうか?

上図のように,比率が小さくなるほど良いのでしょうか? 明らかに,比率が0になった場合,お金は儲からないからです.

理想的な割合はどれぐらいでしょうか?

これは有名なケリー公式で 解決すべき問題です!

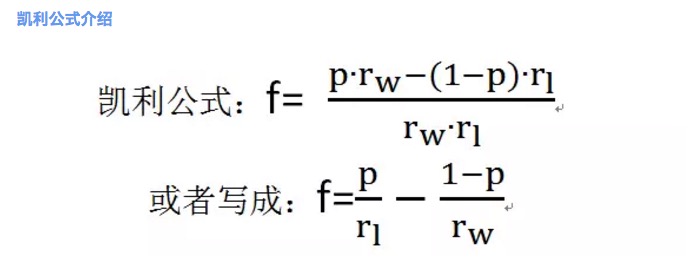2 図

ここでfは最適の賭け比率である。pは勝つ確率である。rwは勝つときの純利益率である,例えば1局でrw=1。rlは負けたときの純損失率である,例えば1局でrl=1。注意rl>0。

ケリー公式によれば,局1で最大の賭けの割合は20%である.

この結論を理解するために,実験をしてみましょう.

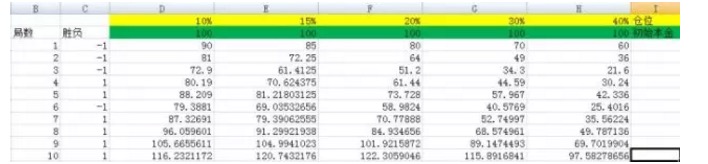3 図

図のように,それぞれ,10%,15%,20%,30%,40%のポジションを設定します. それらの対応する列は,それぞれD,E,F,G,Hです.

実験を3千回繰り返すと 実験を5千回にすると このことから,F列の対応結果が最大で,他の列と比較して圧根は数量級ではないことがわかる。そしてF列の対応比率は20%である。

ケーリー公式の力をご覧下さい. 上記の実験では,もし,確率を40%というH列に運が悪かった場合, 5000回賭けの後に,あなたの本金が100から22799985.75に変わっても,利益は大きいのです. しかし,20%の確率の結果と比較すると,それは本当にお金の無いことと同じです.

これが知識の力だ!

• 3. ケリー公式の理解

ケリー公式の数学推論とその複雑さは,非常に高度で深い数学知識を必要とするため,ここでも議論することは意味がない.ここでは,いくつかの実験を通じて,ケリー公式の主観的な理解を深めていく.

賭け場2: 負ける確率と勝つ確率はそれぞれ50%です.例えばコインを投げるときの純利益率は1で,rw=1で,負ける時の純損失率は0.5で,rl=0.5です.つまり,あなたが1ドルを貯めたとき,勝つとき,あなたは1ドルを勝ち,負けるとき,あなたは5毛しか払わなければいけません.

ギャンブル2の予想利益は0.25で,ギャンブルが非常に優れているギャンブルです.

ケリー公式では,各局の最適な賭け割合は以下のとおりです.

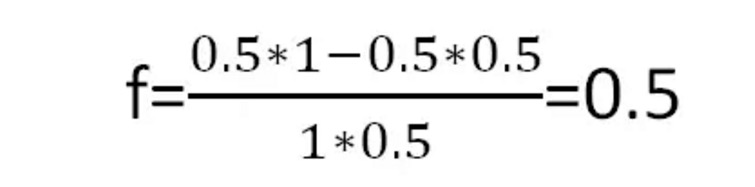グラフ4

長期的に見ると,最大利益を得られるということです.

平均成長率 r の概念を 実験的に導き出します.

実験2.1の2つの図を見てみましょう.

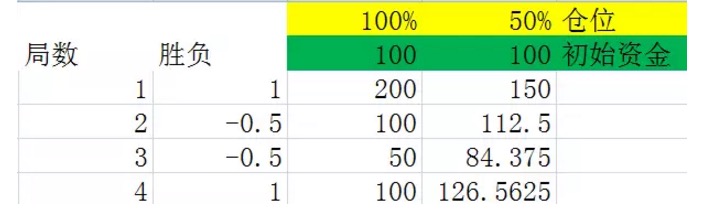グラフ5

この2つの図は,模擬の局2による実験であり,第2列の勝負列では,実験が50%の確率で発生する1,つまり利益100%である。50%の確率で発生する-0.5,つまり損失50%である。第3列および第4列は,それぞれ100%と50%のポジションで,各局後に所有する資金である。

2つの図を注意深く比較すると,結論は1つ,すなわち同じ局数を経て,最終結果はこれらの局数で勝った局数と負けた局数のみに関係しており,これらの局数で勝った局数と負けた局数との順序とは関係ありません.例えば,上記の2つの図で,同じ4局が行われ,同じ図で2勝局が負けたが,最初の図の負けた順番は勝負勝であったが,第二の図の負けた順番は勝負勝負であった.それらの最終結果は同じであった.

この2つの例は,皆さんがよく理解できるほどに十分です.

勝敗の順序は関係ありませんので, 実験2.2のように, 局2を想定します.

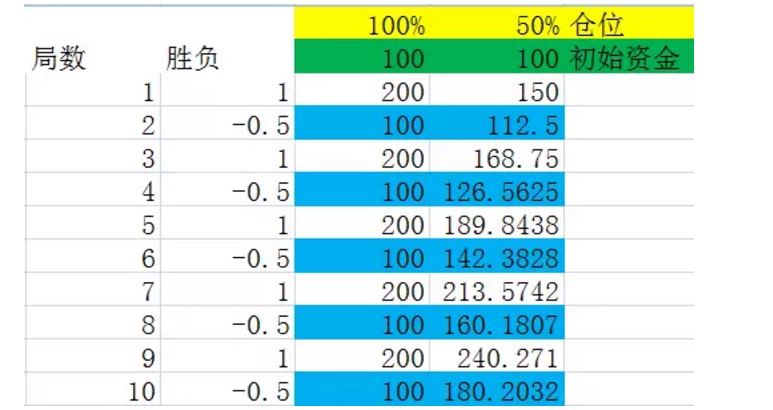グラフ6

勝負が交互に繰り広げられていると仮定すると, 結論は,長期的に見ると,資金が結果に影響を与えないということです.

図を見る前に,まず定義をしましょう.いくつかの局の局を,その確率に等しい結果が出る頻度があり,その全体の局数は,すべての条件を満たす全体の局中数の最小数である整体として見ると仮定すると,この整体を局の集合と呼びます.例えば,上図の実験では,局の集合は,2局の局を行うことを意味し,そのうち1局に勝1局に負けるのです.

上図の青で示された数字をよく見てみると,それらは一組の局の終わりである. これらの数字は安定した成長を維持していることがわかります. ポジションが100%であるとき,青で示された数字の成長率は0%,つまり一組の局の後に資本の成長率は0%です. これはまた,ポジションが充満するたびに賭けても,中期的に局2で儲けられないことを説明します.

これは一般的な法則で,各ストップの後の成長率はポジションと関係している.そして,各ストップの後の成長率が大きいほど,長期的に見れば,最終的な利益も大きい.

各スタッドレスの成長率から,各スタッドレスの平均成長率 g を計算できます.上図では,各スタッドレスのグループに2つのスタッドレスを含んでいるので,各スタッドレスの平均成長率です.

グラフ7

長期的に見ると,資本を最大限に増やすためには,rを最大にするだけで,gを最大化することができる.そして,最適な賭け比率fは,max (g) を解くことで得られる.

• 4. リスクに関するケリー公式の他の結論

ケリー伝説

ケリー公式は,AT&Tベルラボの物理学者ジョン・ラリー・ケリーが,同僚のクロード・エルウッド・シャノンが長距離電話線の雑音に関する研究に基づいて最初に構築したものである.ケリーは,シャノンの情報理論を,内部情報を持つギャンブラーが賭けるときにどのように適用するかという問題を解決した.ギャンブラーは,彼の内部情報が完璧である必要がなく,最高の賭け金額を決定したい,つまり,彼に有用な優位性を与えることができる.ケリーの公式は,シャノンの別の同僚であるエドワード・ソープが,21点と株式市場で適用された. ソープは,残った仕事を活用して,数ヶ月の苦しい計算を経て,21点の選択戦略という数学論文を書いた.彼は,自分の知識を活用して,一晩で奇がネバダレノ市のすべてのカジノを襲い,成功して21点のテーブルから数十万ドルを勝ち取った.彼は,米国ウォール街の定量取引ヘッジファンドの祖先であり,70年代に最初の定量取引ヘッジファンドを創設した.1962年に彼のコラムを出版し,庄家を打ち負かして,金融学の古典の1つとなった.

展望を活用する

カリー公式で現実で稼ぐには? カリー公式の条件を満たすステレオタイプを 作り出すことです. 私の考えでは,このステレオタイプは 金融市場から来ているはずです. 最近,私は取引システムについて研究をしていて,優れた取引システムにとって最も重要なことは何ですか? 利益の期待が正の取引ルールが10%の重要性と,良い資金管理方法が40%の重要性と,残りの50%は人の心理的なコントロールである. カリー公式は,私の資産のポジションをコントロールするのに役立つツールです. 例えば,私が以前研究した株式取引システムでは,毎週取引が成功する確率は0.8で,毎週取引が失敗する確率は0.2である.成功すると3%,失敗すると5%の損失がある.ケリー公式を知らずに,私は盲目的に満仓取引であり,私のポジションが正しく設定されていないことも知らなかった.ケリー公式を使用した後,計算された最良のポジションは9.33であるべきである.つまり,借入利率が0である場合,最も速い資本成長速度を得たい場合は,レバレッジ取引を使用する必要があります.公式を計算することによって,毎週取引の平均成長率rは約7.44%であり,満仓取引の平均資本成長率は約r1.35です. もちろん,ケリー公式は実用的な応用ではそれほど単純にはならないが,多くの困難を乗り越える必要がある.例えば,レバレッジ取引所が必要とする資金のコスト,例えば,現実は資金が無限に分けられるものではない,例えば,金融市場では上記のように単純な局ほど単純ではない. しかし,ケリー公式は,私たちが進むべき道を示しています.