개요
이 전략은 적응형 정규화 이동 평균을 계산하여 다른 시장 간의 중도 거래를 구현합니다. 이 전략은 시장 간 중도, 동적 파라미터 조정, 위험 제어 등의 특징을 가지고 있습니다.
전략 원칙
이 전략은 먼저, 시퀀스를 지정된 범위로 표준화하기 위한 scaleMinimax 함수를 정의한다. 그리고는, 정규화된 이동 평균 rema 함수를 정의하고, 부드럽게 된 신호선을 계산한다. 이 신호선은 다음과 같이 계산된다.
- 슬라이드 창을 정의하고, 기본 길이는 5일이다.
- 매일의 시그값은 전날의 시그값과 당일 종식 가격의 가중된 평균이다. 가중된 평균은 적응 가중제 메커니즘을 사용하며, 현재 값에 가까울수록 무게가 더 크다.
- λ 변수를 정규항으로 추가하여 sig의 변환을 더 부드럽게 한다.
신호선을 얻은 후, 전략은 신호선을 가격과 비교하여 공백을 결정한다. 구체적으로:
- 시그가 가격에 오르면 더 많이 니다.
- 시그하가 가격을 매길 때, 비어있어요.
또한, 이 정책은 평형 인수 smooth를 추가하고, 표시 신호 라인 show_line를 조정 가능한 파라미트로 추가하여, 정책의 유연성을 높였다.
우위 분석
전통적인 이동 평균 전략에 비해 이 전략은 다음과 같은 장점이 있습니다.
- 가격 변화에 더 빨리 대응할 수 있는 자기 적응 가중치 메커니즘을 도입한다.
- 정규화항을 추가하여 신호선을 더 부드럽게 하여 가격의 급격한 변동으로 인해 잘못된 신호가 발생하지 않도록 한다.
- 크로스마켓 중개는 다른 시장의 가격 차이를 이용해서 이익을 얻을 수 있습니다.
- 조정 가능한 매개 변수 디자인은 유연하고 시장 상황에 따라 최적화 할 수 있습니다.
위험과 해결책
이 전략에는 위험도 있습니다.
양방향 교차로에서 잘못된 신호가 발생할 확률이 높습니다. 해결 방법은 적절한 평준화 매개 변수를 조정하여 신호 선의 흔들림을 피하는 것입니다.
크로스 마켓 중개는 두 시장이 가격 관련성이 있고 동향이 일치하는 것을 보장해야합니다. 해결책은 높은 관련성이있는 시장을 선택하여 중개하는 것입니다.
매개 변수 최적화에는 충분한 역사 데이터를 축적하여 재검토해야 한다. 해결책은 실제 거래에서 매개 변수를 신중하게 조정하는 것이다.
최적화 방향
이 전략은 다음과 같은 부분에서 최적화될 수 있습니다.
매개 변수 선택에서, 기계 학습 알고리즘을 도입하여 매개 변수 조합을 자동으로 최적화할 수 있다.
신호 생성에서, 더 많은 지표가 조합되어 더 안정적인 거래 신호를 구성 할 수 있습니다.
리스크 컨트롤에서, 단위 손실을 제어하기 위해 스톱 로드 라인을 설정할 수 있다.
크로스마켓 중개에서는 더 많은 종류의 거래가 가능합니다.
요약하다
이 전략은 이동 평균을 계산하는 방법을 적용하여 시장 간 중도 거래를 구현합니다. 전통적인 이동 평균 전략에 비해, 매개 변수 적응, 부드러운 처리, 시장 간 중도 등의 이점이 있습니다. 다음 단계는 기계 학습, 조합 신호, 위험 관리 등의 방법을 통해 전략을 더 최적화합니다.
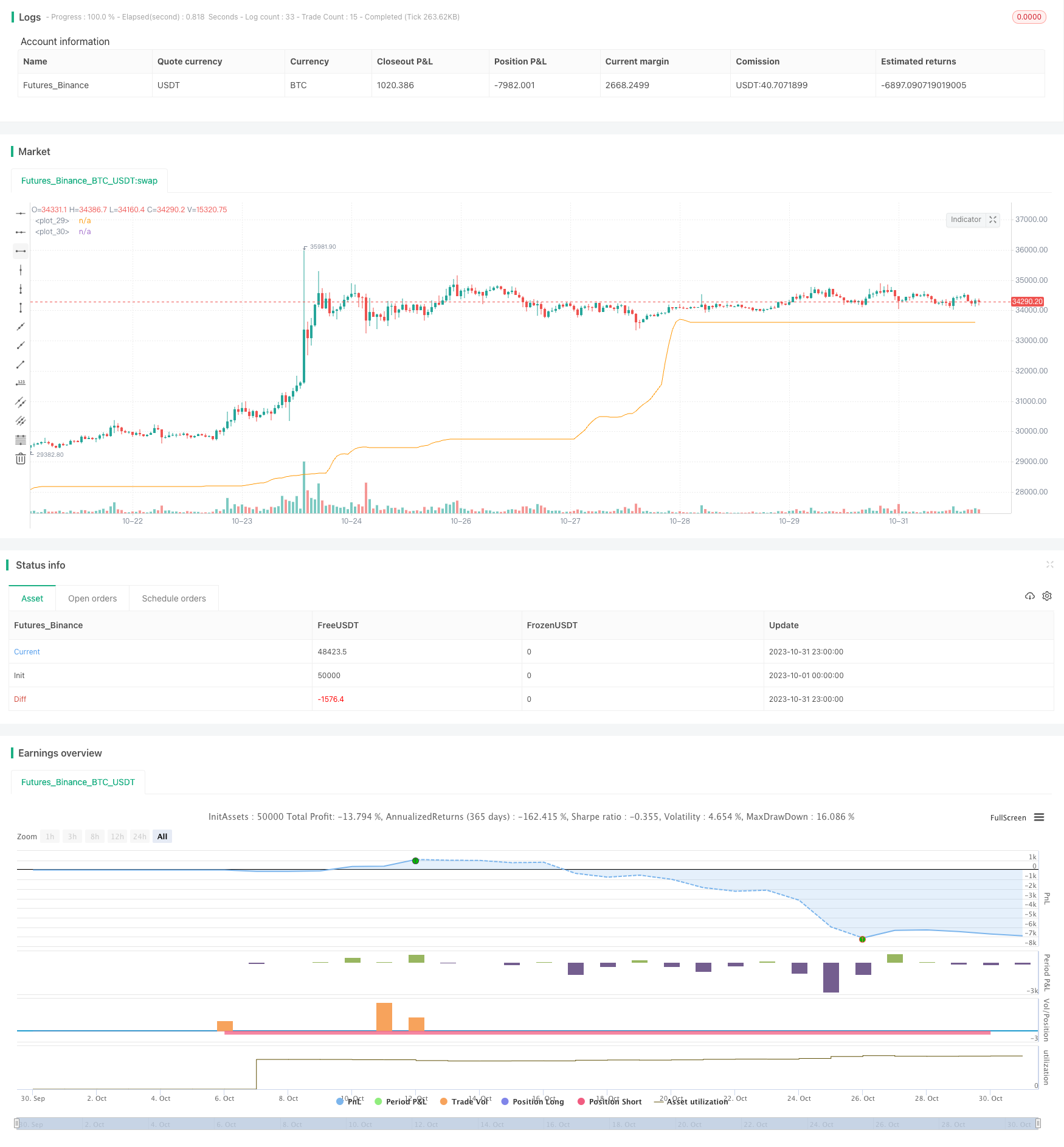
/*backtest
start: 2023-10-01 00:00:00
end: 2023-10-31 23:59:59
period: 1h
basePeriod: 15m
exchanges: [{"eid":"Futures_Binance","currency":"BTC_USDT"}]
*/
//@version=3
strategy("Crossover82%", overlay=true)
//
// Functions
//
scaleMinimax(X, p, min, max) =>
hi = highest(X, p), lo = lowest(X, p)
(max - min) * (X - lo)/(hi - lo) + min
rema(ts, p) => // regularized ma
rm = 0.0, lambda = .5, a = 2 / (p + 1)
rm := (nz(rm[1]) + a * (ts - nz(rm[1])) + lambda * (2 * nz(rm[1]) - nz(rm[2]))) / (lambda + 1)
rm
//
// Inputs
//
X = input(close, title="Data source")
smooth = input(2, title="REMA smooth factor")
show_line = input(true, title="Show signal line")
//
// Main
//
p = 5
sig = rema(scaleMinimax(pow(X*p,-X) - 0.1, 100, lowest(X, 100), highest(X, 100)), smooth)
plot(show_line ? sig : na, linewidth=1)
plot(cross(sig, X) ? ohlc4 : na, style=circles, linewidth=8, color=blue, transp=50)
longCondition = crossover(sig, X)
if (longCondition)
strategy.entry("LE", strategy.long)
shortCondition = crossunder(sig, X)
if (shortCondition)
strategy.entry("SE", strategy.short)