칼만 필터를 기반으로 한 추세 추적 전략

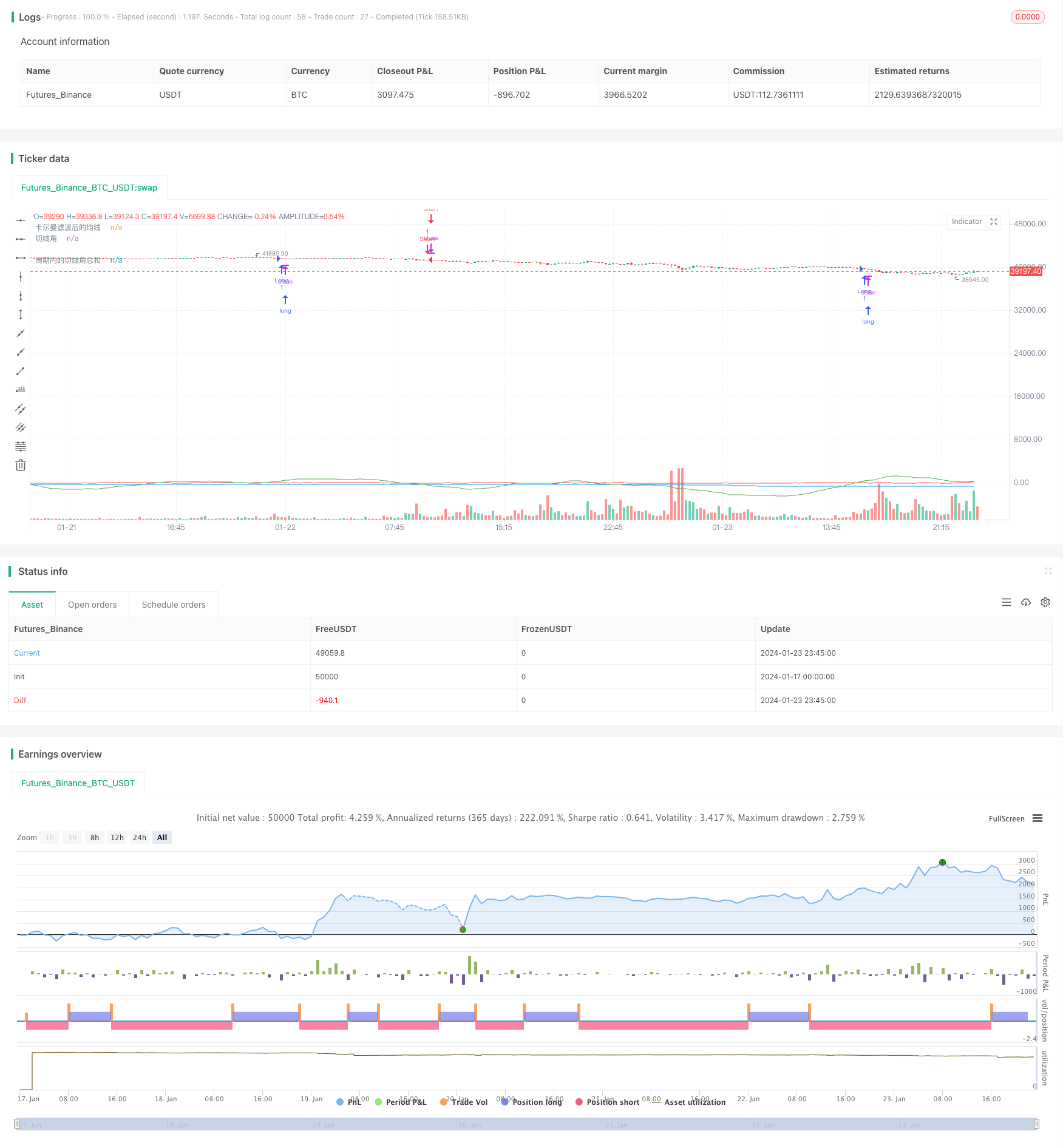
개요

이 전략의 핵심은 칼만 파동 기술을 사용하여 가격 평균선을 평평하게 처리하고, 평평한 후 평균선의 절단 각을 계산하여, 절단 각이 지정된 기간 동안 특정 절벽을 초과할 때 거래 신호를 발생시킨다. 이 전략은 중장선 트렌드를 추적하고, 칼만 파동 기술을 통해 잡음의 영향을 줄여 더 명확하고 신뢰할 수있는 트렌드 신호를 얻는다.

전략 원칙

이 전략의 핵심 논리는 다음과 같은 몇 가지 단계로 구성됩니다.

1. 1분 가격의 간단한 이동 평균 ((SMA) 을 원시 평균선으로 계산한다.

2. 원시 평평선에 칼만 필터링을 하고, 평평한 평평선을 출력한다.

3. 평평한 평평선의 절사각을 계산한다.

4. 매개 변수주기를 정의하고, 통계주기 내의 절사선 각의 합;

5. 주기 내의 세로각의 합이 360도 이상일 때 구매 신호를 생성하고, 360도 이하일 때 판매 신호를 생성한다.

이러한 디자인을 통해, 가격이 위 또는 아래로 추세에 나타나면, 평행선의 직각각은 점차적으로 축적되고, 축적되면 거래 신호를 생성하여 중장선 추세를 효과적으로 추적 할 수 있습니다.

이 중 칼만 파동은 이 전략의 핵심이다. 칼만 파동은 현재 상태를 예측하는 동시에 프로세스 노이즈와 노이즈의 값을 예측하고, 이러한 노이즈의 값을 사용하여 이전 상태의 예측을 정정하여 더 정확하고 신뢰할 수 있는 상태 추정치를 얻는다.

이 전략에서, 가격의 SMA는 상태의 측정으로 볼 수 있으며, 시장 소음에 영향을 받으며, 칼만 필터는 가격의 실제 경향을 회수적으로 추정하여, 소음의 영향을 크게 줄이고, 후속 평균선 연산을 더 신뢰할 수 있게 하여, 더 안정적이고 정확한 거래 신호를 생성한다.

전략적 이점

간단한 이동 평균과 같은 지표 전략에 비해, 이 전략의 가장 큰 장점은 칼만 필터링을 이용한 소음의 영향을 줄여 거래 신호를 더 명확하고 신뢰할 수 있게 만드는 것이다. 구체적인 장점은 주로 다음과 같은 측면에서 나타난다:

1. 가짜 신호를 줄여줍니다. 칼만 필터는 노이스를 적응적으로 추정하고 제거하여 무작위적인 변동으로 인한 많은 가짜 신호를 효과적으로 필터링하여 생성 된 거래 신호를 더 신뢰할 수 있습니다.

2. 더 나은 추적 효과. 평평한 후의 평행선 형태는 더 유동적이며, 가격 중간에 긴 선의 추세를 더 잘 반영하여 더 뛰어난 추세 추적 효과를 달성 할 수 있습니다.

3. 조정 가능한 매개 변수 설정이 유연하다. 조정 가능한 매개 변수는 평균선 길이, 칼만 파동의 매개 변수 및 통계주기를 포함하며, 다른 시장 환경에 유연하게 적응할 수 있다.

4. 위험 조절 가능. 이 전략은 단기 변동보다는 중장기 추세에 더 많은 관심을 두고, 위험과 수익의 균형이 잘 이루어진다.

5. 구현이 간단하고 확장하기 쉽다. 이 전략의 핵심 알고리즘은 간단하고 구현 및 테스트가 쉽으며, 기계 학습 알고리즘의 자동 최적화 파라미터와 같은 확장 공간도 제공합니다.

전략적 위험

이 전략에는 다음과 같은 주요 위험도 있습니다.

1. 트렌드 역전 위험. 이 전략은 트렌드 추적에 초점을 맞추고 있으며, 급격한 트렌드 역전이 발생하면 큰 손실이 발생한다. 통계주기를 적절히 단축하여 단독 손실을 줄일 수 있다.

2. 매개 변수 최적화 위험. 부적절한 매개 변수 설정은 거래 빈도 또는 신호 지연으로 이어질 수 있으며, 충분한 테스트 최적화가 필요합니다. 기계 학습 알고리즘과 결합 가능한 자동 최적화.

3. 과도한 최적화 위험. 역사적 데이터에 대한 과도한 최적화는 또한 매개 변수가 실패할 수 있으며, 샘플 외의 유효성을 제어할 필요가 있다.

4. 구현의 복잡성이 증가하는 위험. 칼만 파동과 절사각 알고리즘을 도입하면 코드 복잡성이 증가하고, 올바른 구현을 보장해야 한다.

전략 최적화 방향

위와 같은 위험 요소를 고려하여, 이 전략의 최적화 방향은 다음과 같습니다.

1. 중지 및 포지션 관리를 도입한다. 적절한 중지로 인해 단위 손실 위험을 효과적으로 제어할 수 있으며, 동적 포지션 관리는 시장 상황에 따라 포지션 커버 리스크를 조정할 수 있다.

2. 자동 매개 변수 최적화. 기계 학습 최적화 알고리즘을 통해 매개 변수의 자동 최적화를 실현할 수 있으며, 과도한 최적화 위험을 피할 수 있다.

3. 다른 지표를 통합한다. 전략에 다른 지표를 통합하여 전략의 안정성을 높이기 위해 지표 포트폴리오를 형성할 수 있다.

4. 효율성 평가를 높여라. 더 많은 위험 조정 지표를 도입하여 전략의 효율성과 안정성을 평가하여 더 포괄적이고 정확한 결론을 도출하십시오.

5. 여러 품종을 확장한다. 효과가 좋다면, 더 많은 품종으로 확장하는 것을 고려할 수 있다. 중·장기적으로 더 풍부한 표본을 축적하고, 또한 다양한 품종의 매개 변수를 최적화할 수 있다.

요약하다

이 전략은 전반적으로 더 간단하고 실용적인 트렌드 추적 전략이다. 전통적인 이동 평균 전략에 비해, 칼만 파동 알고리즘을 도입하는 것이 가장 큰 혁신점이며, 전략이 더 명확하고 신뢰할 수있는 거래 신호를 생성 할 수있게 해줍니다. 다음 단계의 추가 최적화를 통해이 전략은 더 우수한 효과를 얻을 수 있습니다.