মুভিং এভারেজ ওয়েটেড স্ট্যান্ডার্ড ডেভিয়েশন ট্রেডিং কৌশল
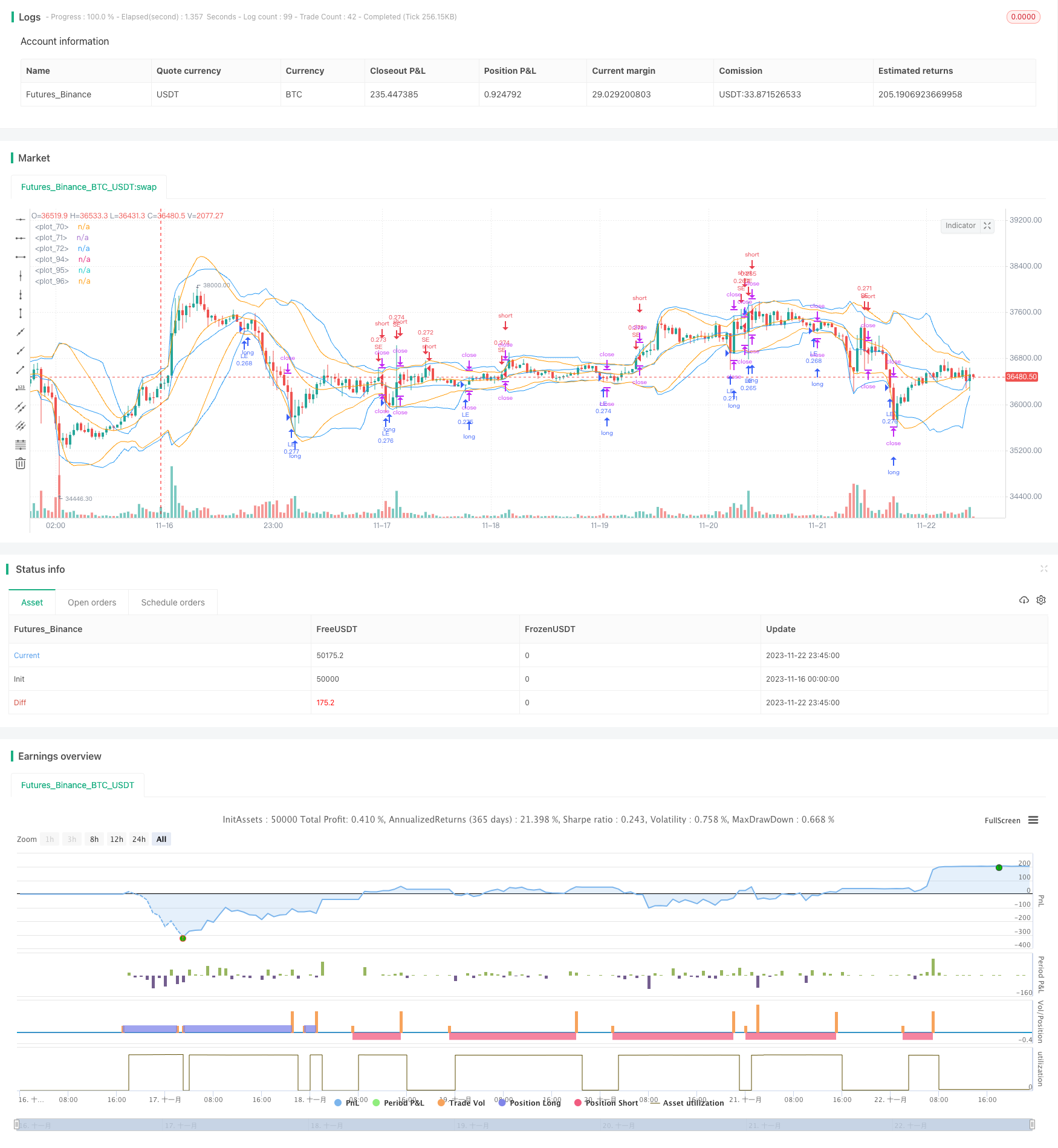
ওভারভিউ
এই কৌশলটি একটি মুদ্রা মুদ্রার প্রবণতা ট্রেডিংয়ের জন্য একটি চলমান গড়ের সাথে যুক্ত একটি ওজনের স্ট্যান্ডার্ড ডিফারেনশিয়াল সূচক ব্যবহার করে। কৌশলটি একটি নির্দিষ্ট সময়ের মধ্যে বন্ধের দাম এবং লেনদেনের পরিমাণের উপর ভিত্তি করে দামের ওজনের স্ট্যান্ডার্ড ডিফারেনশিয়াল চ্যানেল গণনা করে। যখন দামটি চ্যানেলটি ভেঙে যায় তখন অতিরিক্ত খালি করে দেয়। একই সাথে, স্টপ লস স্টপ শর্তগুলি সেট করুন, একক ক্ষতি হ্রাস করুন।
কৌশল নীতি
কোডে দুটি কাস্টম ফাংশন সংজ্ঞায়িত করা হয়েছে, যথাক্রমে টাইম সিকোয়েন্স এবং অ্যারে গণনা থেকে ভারী স্ট্যান্ডার্ড পার্থক্য। প্রধান পদক্ষেপগুলি হলঃ
- সমাপ্তি মূল্য এবং লেনদেনের পরিমাণের উপর ভিত্তি করে ওজনযুক্ত গড় মূল্য গণনা করা হয়েছে
- গড় মানের সাথে K-রেখার ত্রুটির বর্গক্ষেত্র গণনা করুন
- নমুনার পরিমাণ ও ওজনের সাথে সামঞ্জস্য করে গড়ের উপর ভিত্তি করে পার্থক্য গণনা করা হয়
- খোলার মানের পার্থক্য
এইভাবে, আমরা একটি গড় পরিমাপের গড় মূল্যের সাথে একটি গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমাপের গড় পরিমা
সামর্থ্য বিশ্লেষণ
এই কৌশলটির সবচেয়ে বড় সুবিধা হ'ল এটি চলমান গড় এবং ওঠানামা বিশ্লেষণের সংমিশ্রণ। চলমান গড়গুলি বাজারের প্রবণতার দিকনির্দেশ দেয়, স্ট্যান্ডার্ড ডিফারেনশিয়ালগুলি যুক্তিসঙ্গত ব্যাপ্তিগুলি সংজ্ঞায়িত করে, যা পরস্পর যাচাই করে এবং উচ্চ নির্ভরযোগ্যতা দেয়। এছাড়াও, লেনদেনের ভরটি ভুয়া ব্রেকিংয়ের জন্য ফিল্টার করা যায়, প্রকৃত ব্রেকিংয়ের সম্ভাবনা বেশি।
এই কৌশলটি স্টপ লস স্টপওয়েজও সেট করে, যা ট্রেন্ডকে ধরে রাখতে সাহায্য করে এবং বিপরীত দিকে ঘুরতে না গিয়ে অতিরিক্ত ক্ষতির কারণ হয়। এটি এমন একটি বিষয় যা অনেক নতুন খেলোয়াড়ের পক্ষে সম্ভব নয়।
ঝুঁকি বিশ্লেষণ
মূল ঝুঁকিটি হ'ল বাজারটি তীব্রভাবে ওঠানামা করতে পারে। এই সময়ে স্ট্যান্ডার্ড ডিফেন্ডার চ্যানেলটিও ব্যাপকভাবে ওঠানামা করতে পারে, যা বিচারকে প্রভাবিত করে না।
প্রতিকার হিসাবে, চক্রের প্যারামিটারগুলি যথাযথভাবে সামঞ্জস্য করা যেতে পারে, সমতলতা বক্ররেখা। অন্যান্য সূচক যেমন RSI ইত্যাদির সাথে মিলিত হওয়ার বিষয়টিও বিবেচনা করা যেতে পারে, যাতে বিরতির নিশ্চিতকরণের প্রভাব বাড়ানো যায়।
অপ্টিমাইজেশান দিক
- অনুকূলিতকরণ চক্র প্যারামিটারঃ 5 মিনিট, 15 মিনিট, 30 মিনিট ইত্যাদি বিভিন্ন চক্র পরীক্ষা করে সেরা সমন্বয় খুঁজে বের করা যায়
- অপ্টিমাইজ করুন স্টপ-ডাউন-স্টপ অনুপাত। বিভিন্ন স্টপ-ডাউন-স্টপ পয়েন্ট পরীক্ষা করুন এবং সর্বোত্তম রিটার্ন অর্জন করুন
- ফিল্টারিং শর্ত যুক্ত করা হয়েছে। যেমন, সংমিশ্রণ ট্র্যাফিক, মিথ্যা ব্রেকডাউন থেকে Loss এড়ানো
- K-লাইন ইন্টিটিটি কমানোর জন্য, যেমন বন্ধের মূল্যের অবস্থান, ছায়া দৈর্ঘ্য ইত্যাদির মাধ্যমে K-লাইন ইন্টিটিটি নিশ্চিত করা।
সারসংক্ষেপ
এই কৌশলটি সফলভাবে ভারী স্ট্যান্ডার্ড ডিভার্জেন্স সূচক ব্যবহার করে, চলমান গড়ের দিকনির্দেশনা দ্বারা সমর্থিত, ক্রিপ্টোকারেন্সির প্রবণতা অনুসরণ করতে সক্ষম। একই সময়ে, যুক্তিসঙ্গত স্টপ লস স্টপ সেট করা বাজার গতিবেগকে ধরে রাখতে এবং অত্যধিক বিপরীতকরণের ফলে ক্ষতি এড়াতে সহায়তা করে। প্যারামিটার সমন্বয় এবং একাধিক সূচক যাচাইয়ের মাধ্যমে, আরও অপ্টিমাইজ করা যায় এবং একটি নির্ভরযোগ্য পরিমাণযুক্ত ট্রেডিং কৌশল তৈরি করা যায়।
/*backtest
start: 2023-11-16 00:00:00
end: 2023-11-23 00:00:00
period: 45m
basePeriod: 5m
exchanges: [{"eid":"Futures_Binance","currency":"BTC_USDT"}]
*/
// This source code is subject to the terms of the Mozilla Public License 2.0 at https://mozilla.org/MPL/2.0/
// © rumpypumpydumpy © cache_that_pass
//@version=4- 1