Skalieren Sie die normalisierte Vektorhandelsstrategie mit der Aktivierungsfunktionsoptimierung
Erstellungsdatum:
2024-01-22 09:02:30
zuletzt geändert:
2024-01-22 09:02:30
Kopie:
0
Klicks:
578
ChaoZhang
1
konzentrieren Sie sich auf
1617
Anhänger
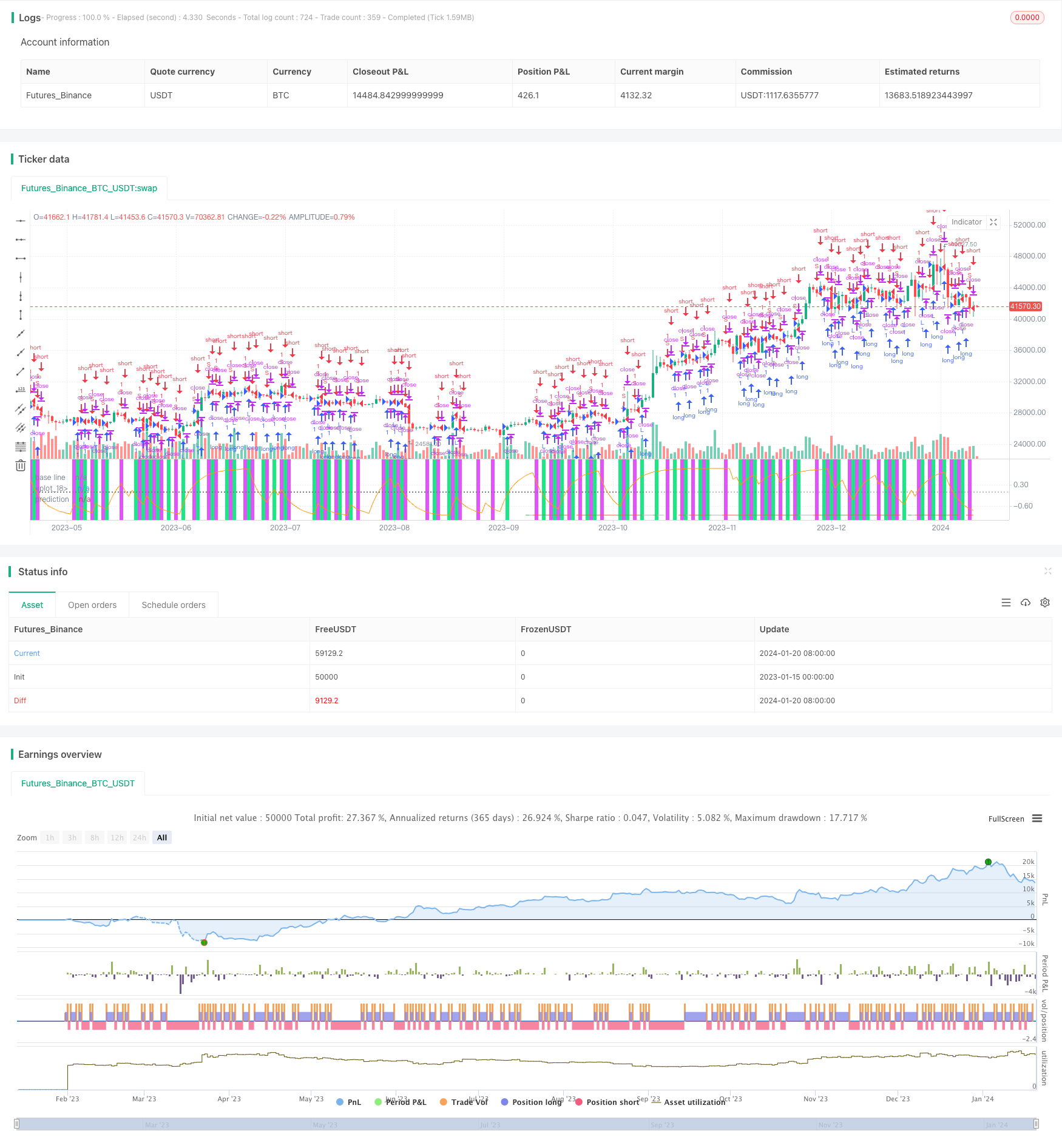
Überblick
Die Strategie ist eine Verbesserung der drkhodakarami-Skala-Einheitlichungs-Vektor-Strategie, die hauptsächlich die Aktivierungsfunktion hinzufügt, um die Leistung der Strategie zu verbessern. Die Strategie nutzt die Zeit-Achs-Differenz, um die Veränderungsrate des Marktes zu berechnen, und macht mehr Leerzeichen durch Tiefstandsurteile.
Strategieprinzip
- Berechnen Sie die prozentualen Veränderungen des Close-Preises auf der festgelegten Zeitlinie x
- Geben Sie x an die Aktivierungsfunktion und erhalten Sie die abgeschlossene Sequenz p
- Positiv-Negativ-Threshold für th, wenn p über th und null über -th ist
- Schalten Sie die Übertragung aus, um falsche Signale zu vermeiden.
Analyse der Stärken
- Einführung einer Aktivierungsfunktion, die Geräusche filtert und die Qualität der Signalentscheidung verbessert
- Neue Logik für die Eröffnung und Schließung von Positionen, die automatisch gehandelt werden können
- Erweiterung der Parameter-Einstellfläche für mehr Märkte
- Die visuelle Gestaltung ist sehr gut und spiegelt die Handelssignale intuitiv wider.
Risikoanalyse
- Fehlgelegte Thresholds können zu verpassten Handelschancen führen
- Die falsche Auswahl der Aktivierungsfunktion kann die Marktinformationen filtern
- Signalverfälschung durch Übertragung zu testen
Die Lösung:
- Anpassung von Threshold-Parametern auf optimale Werte
- Versuche verschiedene Aktivierungsfunktionen und finde die passende
- Hinzufügen von Übertragung der Detektionslogik zur Bestätigung der Signalwirksamkeit
Optimierungsrichtung
- Erhöhung der Anpassungs-Threshold-Einstellung
- Optimierung der Parameter der Aktivierung
- Autostopp-Logik hinzugefügt
- Mehr Faktoren für die Filterung
Zusammenfassen
Die Strategie basiert auf der drkhodakarami und führt eine Aktivierungsfunktion ein, um die Leistung zu verbessern und sich durch die Erweiterung des Parameter-Optimierungsraums besser an die Veränderungen des Marktes anzupassen. Gleichzeitig ist die visuelle Gestaltung hervorragend und spiegelt die Handelsmöglichkeiten intuitiv wider. In der Folge kann die Aktivierungsfunktion mit den Threshold-Einstellungen weiter optimiert und die Stop-Logik mit mehr Signalfilterung hinzugefügt werden, um bessere Strategieeffekte zu erzielen.
Strategiequellcode
/*backtest
start: 2023-01-15 00:00:00
end: 2024-01-21 00:00:00
period: 1d
basePeriod: 1h
exchanges: [{"eid":"Futures_Binance","currency":"BTC_USDT"}]
*/
//@version=4
// author: capissimo
strategy("Scaled Normalized Vector Strategy, ver.4", precision=2, overlay=false)
// This is a modification of my Scaled Normalized Vector Strategy
// original: Drkhodakarami (https://www.tradingview.com/script/Fxv2xFWe-Normalized-Vector-Strategy-By-Drkhodakarami-Opensource/)
price = input(close, "Price Data")
tf = input(18, "Timeframe", minval=1, maxval=1440)
thresh = input(14., "Threshold", minval=.1, step=.1)
div = input(1000000,"Divisor", options=[1,10,100,1000,10000,100000,1000000,10000000,100000000])
mmx = input(233, "Minimax Lookback", options=[1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584])
showVol = input(false, "Volume")
useold = input(true, "Use Old System")
method = input("Swish", "Activation", options=["Step", "LReLU", "Swish", "None"])
scaleMinimax(X, p, min, max) =>
hi = highest(X, p), lo = lowest(X, p)
(max - min) * (X - lo)/(hi - lo) + min
getdiff(prc, tf) =>
prev = scaleMinimax((useold ? security(syminfo.tickerid, tostring(tf), prc[1], barmerge.gaps_off, barmerge.lookahead_on)
: security(syminfo.tickerid, tostring(tf), prc[1])), tf, 0, 1)
curr = scaleMinimax((useold ? security(syminfo.tickerid, tostring(tf), hlc3, barmerge.gaps_off, barmerge.lookahead_on)
: security(syminfo.tickerid, tostring(tf), hlc3)), tf, 0, 1)
(curr/prev) - 1
relu(x) => max(x, 0)
lrelu(x, alpha) => relu(x) - alpha * relu(-x)
step(x) => x >= 0 ? 1 : -1
log2(x) => log(x) / log(2)
sigmoid(x) => 1 / (1 + exp(-x))
swish(x) => x * sigmoid(x)
f(m) => method==m
vol = useold ? security(syminfo.tickerid, tostring(tf), volume, barmerge.gaps_off, barmerge.lookahead_on)
: security(syminfo.tickerid, tostring(tf), volume)
obv = cum(change(price) > 0 ? vol : change(price) < 0 ? -vol : 0*vol)
prix = showVol ? obv : price
x = getdiff(prix, tf)
p = f("Swish") ? swish(x) : f("Step") ? step(x) : f("LReLU") ? lrelu(x, .8) : x
th = thresh/div
long = crossover(p, th)
short= crossunder(p, -th)
lime = color.new(color.lime, 10), fuchsia = color.new(color.fuchsia, 10),
black = color.new(color.black, 100), gray = color.new(color.gray, 50)
bg = long ? lime : short ? fuchsia : black
cl = p > th ? color.green : p < -th ? color.red : color.silver
bgcolor(bg, editable=false)
plot(scaleMinimax(th, mmx, -1, 1), color=lime, editable=false, transp=0)
hline(0, linestyle=hline.style_dotted, title="base line", color=gray, editable=false)
plot(scaleMinimax(-th, mmx, -1, 1), color=fuchsia, editable=false, transp=0)
plot(scaleMinimax(p, mmx, -1, 1), color=cl, style=plot.style_histogram, transp=70, editable=false)
plot(scaleMinimax(p, mmx, -1, 1), color=cl, style=plot.style_linebr, title="prediction", transp=0, editable=false)
strategy.entry("L", true, 1, when=long)
strategy.entry("S", false, 1, when=short)
alertcondition(long, title='Long', message='Long Signal!')
alertcondition(short, title='Short', message='Short Signal!')
//*** Karobein Oscillator
per = input(8, "Karobein Osc Lookback")
prix2 = ema(price, per)
a = ema(prix2 < prix2[1] ? prix2/prix2[1] : 0, per)
b = ema(prix2 > prix2[1] ? prix2/prix2[1] : 0, per)
c = (prix2/prix2[1])/(prix2/prix2[1] + b)
d = 2*((prix2/prix2[1])/(prix2/prix2[1] + c*a)) - 1
plot(scaleMinimax(d, mmx, -1, 1), color=color.orange, transp=0)