Estratégia de Previsão de Ondas Gaussianas

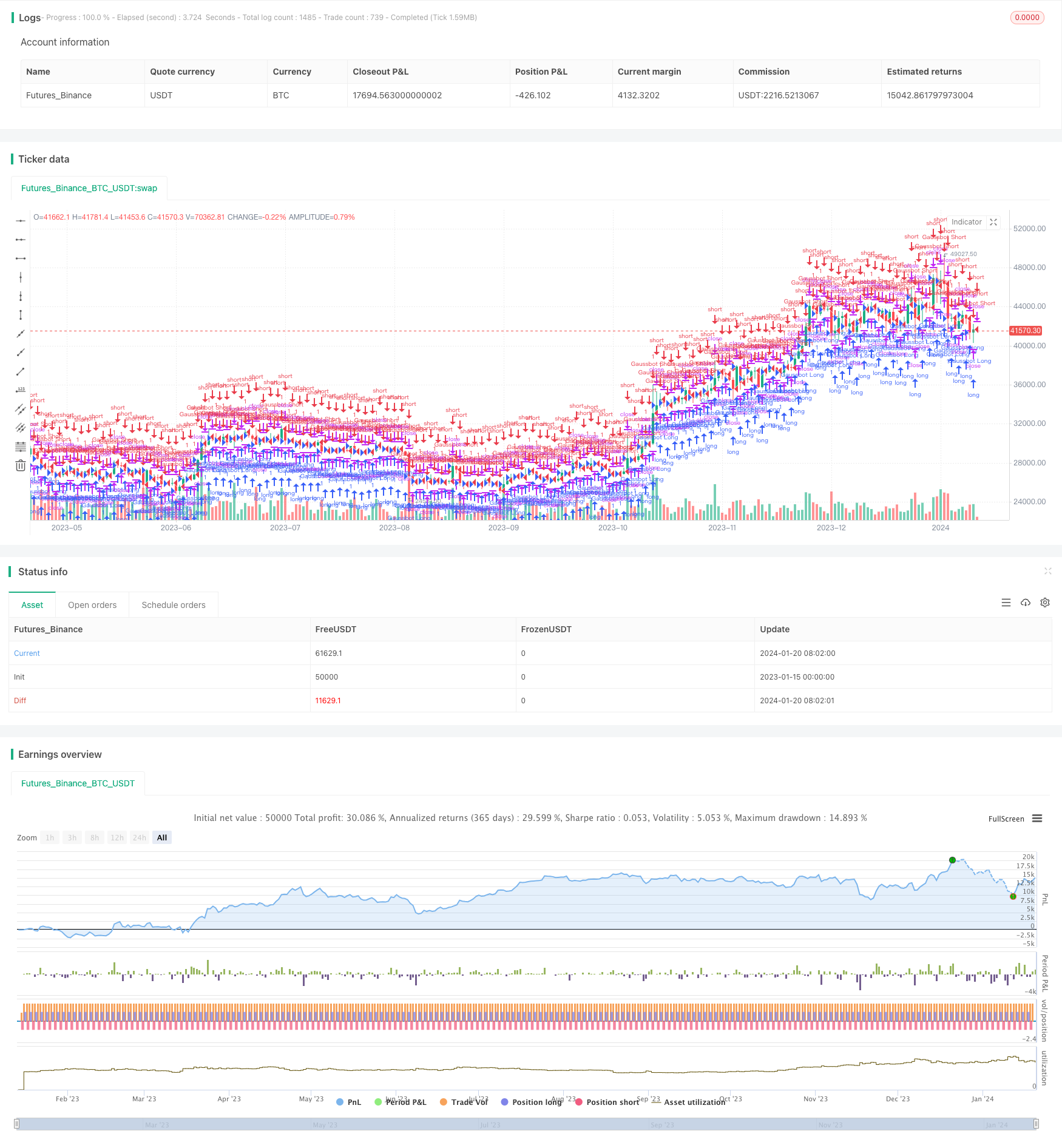
Visão geral

A estratégia de previsão de ondas de Gauss é uma estratégia de negociação quantitativa baseada em ondas de Gauss. Utiliza as características de suavização das ondas de Gauss para filtrar várias vezes a sequência de preços, gerando várias sequências de preços após suavização.

Princípio da estratégia

O núcleo da estratégia é o algoritmo de Gauss. O filtro de Gauss é um filtro de suavização linear que usa a função de Gauss como peso. A estratégia define o parâmetro p como o tamanho da janela de filtro.[i] representa o resultado de i vezes a onda de Gauss sobre a sequência de preços original.

A estratégia usa a ideia da recorrência. Primeiro, com a sequência de preços alfa e original price, calcula-se a primeira onda ret. Em seguida, com base em ret, a segunda onda é feita, obtendo ret2 repetido várias vezes. Finalmente, a combinação de várias sequências de preços, compõe-se uma curva para prever o preço futuro ret4. Se o preço previsto for maior que o preço real atual, faça mais; Se for menor que o preço atual, faça zero.

Assim, através de várias ondas de filtragem, pode ser mais suave e combinar tendências. Ao mesmo tempo, a combinação de várias combinações permite a previsão de movimentos de preços no curto prazo.

Análise de vantagens

A estratégia tem as seguintes vantagens:

1. O uso de ondas de alta freqüência para suavizar o preço. Pode filtrar eficazmente o ruído de alta freqüência, tornando a estratégia mais estável.

2. O uso de filtragem recorrente em várias ondas permite uma melhor adaptação das tendências de preços e uma melhor previsão.

3. Preços de previsão de simulação baseados em múltiplos formulários. Pode modelar movimentos de preços de curto prazo, gerando assim um sinal de negociação.

4. Combinação de preços atuais com preços de previsão. Os sinais de negociação são combinados diretamente com a previsão de tendências para evitar oportunidades de negociação perdidas.

5. A implementação é simples, fácil de entender e de otimizar. Pode ser usado como um módulo básico de estratégia de alta frequência, estendendo-se a outros indicadores de análise.

Análise de Riscos

A estratégia também apresenta os seguintes riscos:

1. Os filtros de Gauss podem ser usados para suavizar mudanças bruscas de preços, podendo perder oportunidades de negociação de curto prazo.

2. Há um risco de sobre-conformidade na adaptação de múltiplos modelos. Se o padrão de mudança de preço for mutante, isso reduzirá a eficácia da previsão.

3. O tamanho da janela de filtro e o número de fases de integração de polinômios precisam ser definidos com precisão. Se não for adequado, pode falhar.

4. Dependendo apenas do preço de abertura como sinal de negociação. Não é possível realizar operações de negociação no disco interno.

Direção de otimização

A estratégia pode ser otimizada em:

1. Aumentar o treinamento do modelo e o mecanismo de retreinamento da janela de deslizamento. Permitir o ajuste dinâmico dos parâmetros da política, reduzindo o risco de sobreajuste.

2. Combinando mais indicadores e características de preços. Input estratégico rico, fazendo previsões mais estáveis.

3. Aumentar o mecanismo de suspensão de perdas. Definir a proporção máxima de perdas para evitar que os eventos extremos causem perdas significativas.

4. Optimizar o gerenciamento de posições. Ajustar posições de forma dinâmica com base na precisão de previsão e na volatilidade.

5. Tente fazer previsões baseadas em modelos de aprendizagem de máquina convencionais. Modelos de aprendizagem profunda, como o LSTM. Aumente ainda mais a capacidade de previsão de estratégias.

Resumir

Em geral, esta estratégia é uma estratégia de quantificação de alta frequência que utiliza as ondas de Gauss e a simulação de múltiplos termos para fazer previsões de preços. Ela tem certas vantagens, mas também há espaço para melhorias.