Gaussian Channel Adaptive Moving Average Strategy
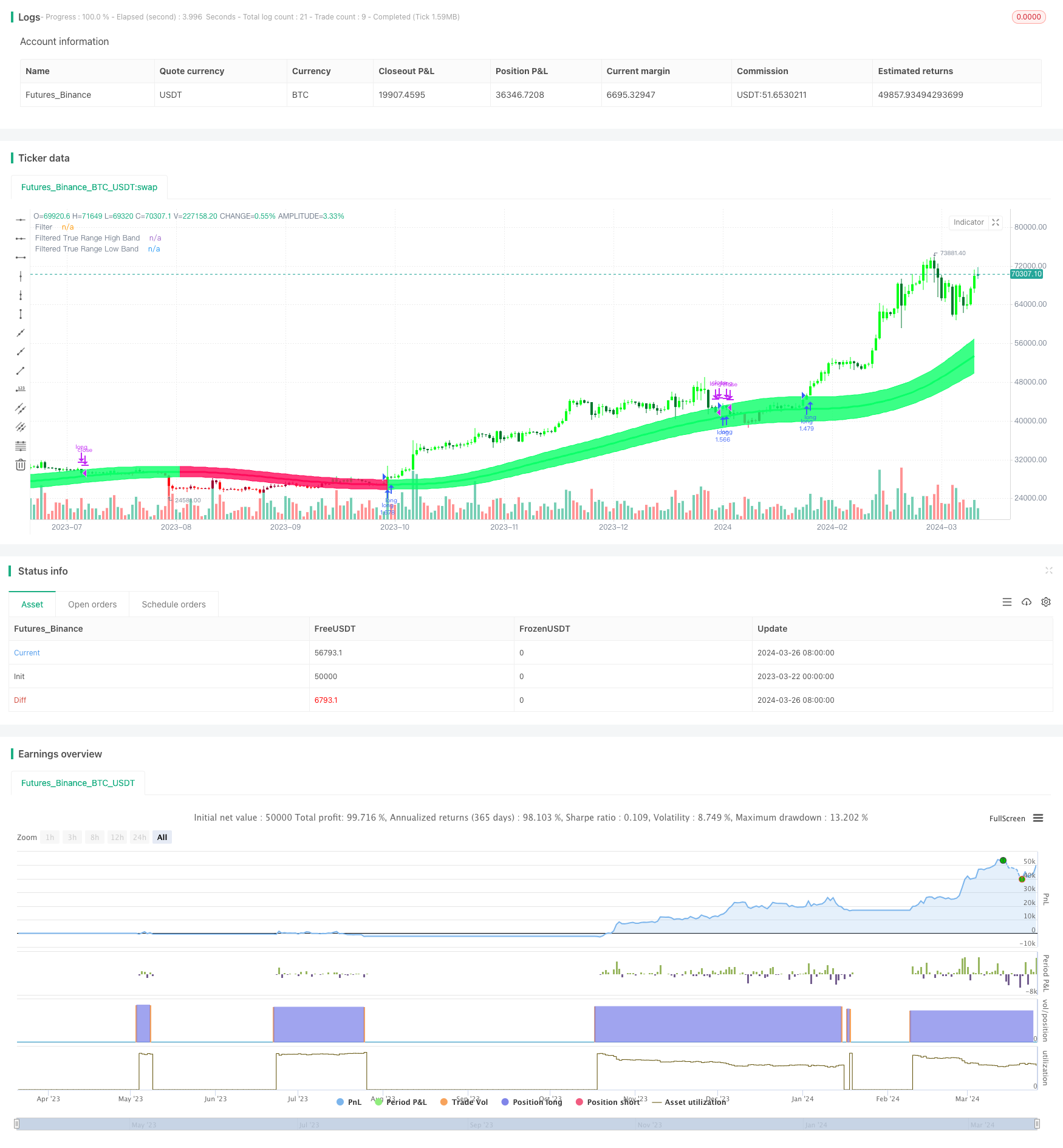
جائزہ
گوسٹ چینل خودکشی یکساں حکمت عملی ایک مقداری تجارتی حکمت عملی ہے جس میں گوسٹ لہر ٹیکنالوجی اور خودکشی پیرامیٹرز کی ترتیب کا استعمال کیا جاتا ہے۔ یہ حکمت عملی جان ایہلرز کی تجویز کردہ گوسٹ لہراتی نظریہ پر مبنی ہے ، جس میں قیمت کے اعداد و شمار پر متعدد اشاریہ منتقل اوسط کی حساب کتاب کرکے ہموار اور خودکشی کرنے والا تجارتی سگنل تیار کیا جاتا ہے۔ حکمت عملی کا بنیادی مقصد ایک متحرک ایڈجسٹ قیمت چینل کی تعمیر کرنا ہے ، جس میں قیمتوں میں اضافے اور کمی کے بعد قیمتوں میں اضافے کے بعد قیمتوں میں اضافے کے بعد قیمتوں میں اضافے کے بعد قیمتوں میں اضافے کے بعد قیمتوں میں اضافے کے بعد قیمتوں میں اضافے کے بعد قیمتوں میں اضافے کے بعد قیمتوں میں اضافے کے بعد قیمتوں میں اضافے کے بعد قیمتوں میں اضافے کے بعد قیمتوں میں اضافے کے بعد قیمتوں میں اضافہ ہوتا ہے۔ جب قیمتیں ٹوٹ جاتی ہیں تو خریدیں اور ٹوٹ جاتی ہیں جب وہ ٹوٹ جاتی ہیں۔
حکمت عملی کا اصول
گوسٹ چینل خود کو یکساں لکیری حکمت عملی کے اصول مندرجہ ذیل ہیں:
- قیمتوں کے گوسٹن ویوئل کی گنتی کریں۔ بیٹا اور الفا پیرامیٹرز کا حساب صارف کے ذریعہ ترتیب دیئے گئے نمونہ کی مدت اور قطبوں کی تعداد کے مطابق کیا جاتا ہے ، پھر قیمت کے اعداد و شمار کو گوسٹن ویوئل کی درجہ بندی کی جاتی ہے ، جس سے قیمتوں کا سلسلہ ہموار ہوجاتا ہے۔
- قیمتوں کی حقیقی اتار چڑھاو کی ایک ہی گوسٹن لہر کا علاج ، اتار چڑھاو کی ایک ہموار ترتیب حاصل کریں۔
- Gaussian چینل کی تعمیر ◄ Gaussian سٹرنگ کے بعد قیمت کے طور پر ایک متحرک چینل بنانے کے لئے، ایک متحرک چینل بنانے کے لئے، ایک متحرک چینل بنانے کے لئے، ایک متحرک چینل بنانے کے لئے، ایک متحرک چینل بنانے کے لئے، ایک متحرک چینل بنانے کے لئے.
- ٹریڈنگ سگنل پیدا کرنا۔ جب قیمت اوپر کی طرف سے چینل کو ٹریک کرتی ہے تو ، خریدنے کا سگنل پیدا ہوتا ہے۔ جب قیمت نیچے کی طرف سے چینل کو ٹریک کرتی ہے تو ، فروخت کا سگنل پیدا ہوتا ہے۔
- ٹائم فریم پیرامیٹرز متعارف کروائیں۔ صارف حکمت عملی کو چلانے کے لئے شروع اور ختم ہونے کا وقت مقرر کرسکتا ہے ، اس وقت کے دوران حکمت عملی تجارتی سگنل کے مطابق کام کرے گی۔
طاقت کا تجزیہ
گوسٹ چینل کے مطابق ڈھالنے والی یکساں حکمت عملی کے درج ذیل فوائد ہیں:
- خود کو اپنانے والا۔ حکمت عملی متحرک طور پر ایڈجسٹ کرنے والے پیرامیٹرز کو اپناتی ہے ، جو مارکیٹ کی مختلف حالتوں اور تجارت کی اقسام کے مطابق ڈھال سکتی ہے ، جس میں بار بار دستی ڈیبگنگ کی ضرورت نہیں ہے۔
- رجحانات کا سراغ لگانا اچھا ہے۔ قیمتوں کے چینلز کی تعمیر کے ذریعہ ، حکمت عملی مارکیٹ کے رجحانات کو بہتر طور پر پکڑنے اور ان کی پیروی کرنے کے قابل ہے ، اور اس سے مارکیٹ میں جھوٹے اشاروں سے بچنے میں مدد ملتی ہے۔
- اچھی ہمواریت۔ قیمت کے اعداد و شمار کو متعدد بار ہموار کرنے کے لئے گاسسٹرونک ٹیکنالوجی کا استعمال کرتے ہوئے ، مارکیٹ کے زیادہ تر شور کو ہٹا دیا گیا ، جس سے تجارتی سگنل زیادہ قابل اعتماد ہے۔
- اعلی لچکدار۔ صارف حکمت عملی کے پیرامیٹرز کو اپنی ضرورت کے مطابق ایڈجسٹ کرسکتا ہے ، جیسے نمونہ کی مدت ، قطب نمبر ، اتار چڑھاؤ کے ضارب وغیرہ ، حکمت عملی کی کارکردگی کو بہتر بنانے کے لئے۔
- عملی طور پر مضبوط۔ ٹائم فریم پیرامیٹرز متعارف کرایا گیا ہے ، جس سے حکمت عملی کو مخصوص وقت کی حد میں چلایا جاسکتا ہے ، جس سے ریل اسٹیٹ ایپلی کیشنز اور ریٹرننگ ریسرچ میں آسانی ہوتی ہے۔
خطرے کا تجزیہ
گو کہ گوسٹ چینل کی لچکدار اور یکساں حکمت عملی کے بہت سے فوائد ہیں ، لیکن اس میں کچھ خطرات بھی ہیں:
- پیرامیٹرز کی ترتیب کا خطرہ۔ غلط پیرامیٹرز کی ترتیب سے حکمت عملی کی ناکامی یا خراب کارکردگی کا سبب بن سکتا ہے ، لہذا عملی اطلاق میں بار بار جانچ اور اصلاح کی ضرورت ہے۔
- اچانک واقعات کا خطرہ۔ کچھ اچانک اہم واقعات کے سامنے ، حکمت عملی کو نقصان پہنچانے کے لئے بروقت ردعمل میں ناکامی کا سامنا کرنا پڑ سکتا ہے۔
- زیادہ سے زیادہ فٹ ہونے کا خطرہ۔ اگر پیرامیٹرز کو تاریخی اعداد و شمار سے زیادہ فٹ کرنے کے لئے ترتیب دیا گیا ہے تو ، اس سے حکمت عملی کی مستقبل میں ناقص کارکردگی کا سبب بن سکتا ہے ، جس میں نمونے کے اندر اور باہر کی کارکردگی کو مدنظر رکھنا پڑتا ہے۔
- بیعانہ کا خطرہ۔ حکمت عملی بنیادی طور پر رجحاناتی مارکیٹوں میں لاگو ہوتی ہے ، اور اگر آپ ہلچل والے بازاروں میں کثرت سے تجارت کرتے ہیں تو آپ کو زیادہ بیعانہ کا خطرہ لاحق ہوسکتا ہے۔
اصلاح کی سمت
گوسٹ چینل کی یکساں لائن حکمت عملی کو بہتر بنانے کی سمت میں شامل ہیں:
- متحرک پیرامیٹرز کی اصلاح۔ مشین لرننگ جیسی ٹیکنالوجیز متعارف کرانے کے ذریعے حکمت عملی کے پیرامیٹرز کی خودکار اصلاح اور متحرک ایڈجسٹمنٹ ، موافقت کو بہتر بنانا۔
- ملٹی فیکٹر انضمام: دیگر موثر تکنیکی اشارے یا عوامل کو گاسٹ چینل کے ساتھ جوڑ کر ایک زیادہ مستحکم تجارتی سگنل تشکیل دینا۔
- پوزیشن مینجمنٹ کو بہتر بنائیں۔ حکمت عملی کی بنیاد پر پوزیشن مینجمنٹ اور فنڈ مینجمنٹ کے مناسب قواعد شامل کریں ، واپسی اور خطرے پر قابو پالیں۔
- کثیر قسم کے تعاون۔ اس حکمت عملی کو متعدد مختلف قسم کے لین دین میں پھیلائیں تاکہ اثاثوں کی تعیناتی اور وابستگی کے تجزیے کے ذریعہ خطرہ پھیلائے۔
خلاصہ کریں۔
گوسٹ چینل خود کو اپنانے والی یکساں حکمت عملی ایک ایسی حکمت عملی ہے جو گوسٹ کی لہر اور خود کو اپنانے والے پیرامیٹرز پر مبنی ہے ، جس میں قیمتوں کے چینل کو متحرک طور پر تعمیر کرکے ہموار اور قابل اعتماد تجارتی سگنل تیار کیے جاتے ہیں۔ حکمت عملی میں مضبوط موافقت ، رجحان کی پیروی ، اعلی ہموار ، لچکدار ، عملی اور مضبوط فوائد ہیں ، لیکن اس کے ساتھ ہی پیرامیٹرز کی ترتیب ، غیر متوقع واقعات ، اوور فٹ اور سودے بازی جیسے خطرات کا سامنا کرنا پڑتا ہے۔ متحرک پیرامیٹرز کی اصلاح ، کثیر عنصر کے امتزاج ، پوزیشن مینجمنٹ کی اصلاح ، کثیر قسم کے ہم آہنگی اور دیگر پہلوؤں سے حکمت عملی کو مزید بہتر اور بہتر بنایا جاسکتا ہے۔
/*backtest
start: 2023-03-22 00:00:00
end: 2024-03-27 00:00:00
period: 1d
basePeriod: 1h
exchanges: [{"eid":"Futures_Binance","currency":"BTC_USDT"}]
*/
//@version=4
strategy(title="Gaussian Channel Strategy v1.0", overlay=true, calc_on_every_tick=false, initial_capital=10000, default_qty_type=strategy.percent_of_equity, default_qty_value=100, commission_type=strategy.commission.percent, commission_value=0.1)
// Date condition inputs
startDate = input(title="Date Start", type=input.time, defval=timestamp("1 Jan 2018 00:00 +0000"), group="Dates")
endDate = input(title="Date End", type=input.time, defval=timestamp("31 Dec 2060 23:59 +0000"), group="Dates")
timeCondition = true
// This study is an experiment utilizing the Ehlers Gaussian Filter technique combined with lag reduction techniques and true range to analyze trend activity.
// Gaussian filters, as Ehlers explains it, are simply exponential moving averages applied multiple times.
// First, beta and alpha are calculated based on the sampling period and number of poles specified. The maximum number of poles available in this script is 9.
// Next, the data being analyzed is given a truncation option for reduced lag, which can be enabled with "Reduced Lag Mode".
// Then the alpha and source values are used to calculate the filter and filtered true range of the dataset.
// Filtered true range with a specified multiplier is then added to and subtracted from the filter, generating a channel.
// Lastly, a one pole filter with a N pole alpha is averaged with the filter to generate a faster filter, which can be enabled with "Fast Response Mode".
//Custom bar colors are included.
//Note: Both the sampling period and number of poles directly affect how much lag the indicator has, and how smooth the output is.
// Larger inputs will result in smoother outputs with increased lag, and smaller inputs will have noisier outputs with reduced lag.
// For the best results, I recommend not setting the sampling period any lower than the number of poles + 1. Going lower truncates the equation.
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
//Updates:
// Huge shoutout to @e2e4mfck for taking the time to improve the calculation method!
// -> migrated to v4
// -> pi is now calculated using trig identities rather than being explicitly defined.
// -> The filter calculations are now organized into functions rather than being individually defined.
// -> Revamped color scheme.
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
//Functions - courtesy of @e2e4mfck
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
//Filter function
f_filt9x (_a, _s, _i) =>
int _m2 = 0, int _m3 = 0, int _m4 = 0, int _m5 = 0, int _m6 = 0,
int _m7 = 0, int _m8 = 0, int _m9 = 0, float _f = .0, _x = (1 - _a)
// Weights.
// Initial weight _m1 is a pole number and equal to _i
_m2 := _i == 9 ? 36 : _i == 8 ? 28 : _i == 7 ? 21 : _i == 6 ? 15 : _i == 5 ? 10 : _i == 4 ? 6 : _i == 3 ? 3 : _i == 2 ? 1 : 0
_m3 := _i == 9 ? 84 : _i == 8 ? 56 : _i == 7 ? 35 : _i == 6 ? 20 : _i == 5 ? 10 : _i == 4 ? 4 : _i == 3 ? 1 : 0
_m4 := _i == 9 ? 126 : _i == 8 ? 70 : _i == 7 ? 35 : _i == 6 ? 15 : _i == 5 ? 5 : _i == 4 ? 1 : 0
_m5 := _i == 9 ? 126 : _i == 8 ? 56 : _i == 7 ? 21 : _i == 6 ? 6 : _i == 5 ? 1 : 0
_m6 := _i == 9 ? 84 : _i == 8 ? 28 : _i == 7 ? 7 : _i == 6 ? 1 : 0
_m7 := _i == 9 ? 36 : _i == 8 ? 8 : _i == 7 ? 1 : 0
_m8 := _i == 9 ? 9 : _i == 8 ? 1 : 0
_m9 := _i == 9 ? 1 : 0
// filter
_f := pow(_a, _i) * nz(_s) +
_i * _x * nz(_f[1]) - (_i >= 2 ?
_m2 * pow(_x, 2) * nz(_f[2]) : 0) + (_i >= 3 ?
_m3 * pow(_x, 3) * nz(_f[3]) : 0) - (_i >= 4 ?
_m4 * pow(_x, 4) * nz(_f[4]) : 0) + (_i >= 5 ?
_m5 * pow(_x, 5) * nz(_f[5]) : 0) - (_i >= 6 ?
_m6 * pow(_x, 6) * nz(_f[6]) : 0) + (_i >= 7 ?
_m7 * pow(_x, 7) * nz(_f[7]) : 0) - (_i >= 8 ?
_m8 * pow(_x, 8) * nz(_f[8]) : 0) + (_i == 9 ?
_m9 * pow(_x, 9) * nz(_f[9]) : 0)
//9 var declaration fun
f_pole (_a, _s, _i) =>
_f1 = f_filt9x(_a, _s, 1), _f2 = (_i >= 2 ? f_filt9x(_a, _s, 2) : 0), _f3 = (_i >= 3 ? f_filt9x(_a, _s, 3) : 0)
_f4 = (_i >= 4 ? f_filt9x(_a, _s, 4) : 0), _f5 = (_i >= 5 ? f_filt9x(_a, _s, 5) : 0), _f6 = (_i >= 6 ? f_filt9x(_a, _s, 6) : 0)
_f7 = (_i >= 2 ? f_filt9x(_a, _s, 7) : 0), _f8 = (_i >= 8 ? f_filt9x(_a, _s, 8) : 0), _f9 = (_i == 9 ? f_filt9x(_a, _s, 9) : 0)
_fn = _i == 1 ? _f1 : _i == 2 ? _f2 : _i == 3 ? _f3 :
_i == 4 ? _f4 : _i == 5 ? _f5 : _i == 6 ? _f6 :
_i == 7 ? _f7 : _i == 8 ? _f8 : _i == 9 ? _f9 : na
[_fn, _f1]
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
//Inputs
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
//Source
src = input(defval=hlc3, title="Source")
//Poles
int N = input(defval=4, title="Poles", minval=1, maxval=9)
//Period
int per = input(defval=144, title="Sampling Period", minval=2)
//True Range Multiplier
float mult = input(defval=1.414, title="Filtered True Range Multiplier", minval=0)
//Lag Reduction
bool modeLag = input(defval=false, title="Reduced Lag Mode")
bool modeFast = input(defval=false, title="Fast Response Mode")
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
//Definitions
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
//Beta and Alpha Components
beta = (1 - cos(4*asin(1)/per)) / (pow(1.414, 2/N) - 1)
alpha = - beta + sqrt(pow(beta, 2) + 2*beta)
//Lag
lag = (per - 1)/(2*N)
//Data
srcdata = modeLag ? src + (src - src[lag]) : src
trdata = modeLag ? tr(true) + (tr(true) - tr(true)[lag]) : tr(true)
//Filtered Values
[filtn, filt1] = f_pole(alpha, srcdata, N)
[filtntr, filt1tr] = f_pole(alpha, trdata, N)
//Lag Reduction
filt = modeFast ? (filtn + filt1)/2 : filtn
filttr = modeFast ? (filtntr + filt1tr)/2 : filtntr
//Bands
hband = filt + filttr*mult
lband = filt - filttr*mult
// Colors
color1 = #0aff68
color2 = #00752d
color3 = #ff0a5a
color4 = #990032
fcolor = filt > filt[1] ? #0aff68 : filt < filt[1] ? #ff0a5a : #cccccc
barcolor = (src > src[1]) and (src > filt) and (src < hband) ? #0aff68 : (src > src[1]) and (src >= hband) ? #0aff1b : (src <= src[1]) and (src > filt) ? #00752d :
(src < src[1]) and (src < filt) and (src > lband) ? #ff0a5a : (src < src[1]) and (src <= lband) ? #ff0a11 : (src >= src[1]) and (src < filt) ? #990032 : #cccccc
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
//Outputs
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
//Filter Plot
filtplot = plot(filt, title="Filter", color=fcolor, linewidth=3)
//Band Plots
hbandplot = plot(hband, title="Filtered True Range High Band", color=fcolor)
lbandplot = plot(lband, title="Filtered True Range Low Band", color=fcolor)
//Channel Fill
fill(hbandplot, lbandplot, title="Channel Fill", color=fcolor, transp=80)
//Bar Color
barcolor(barcolor)
longCondition = crossover(close, hband) and timeCondition
closeAllCondition = crossunder(close, hband) and timeCondition
if longCondition
strategy.entry("long", strategy.long)
if closeAllCondition
strategy.close("long")