Estrategia cuantitativa basada en el punto de intersección de la regresión lineal

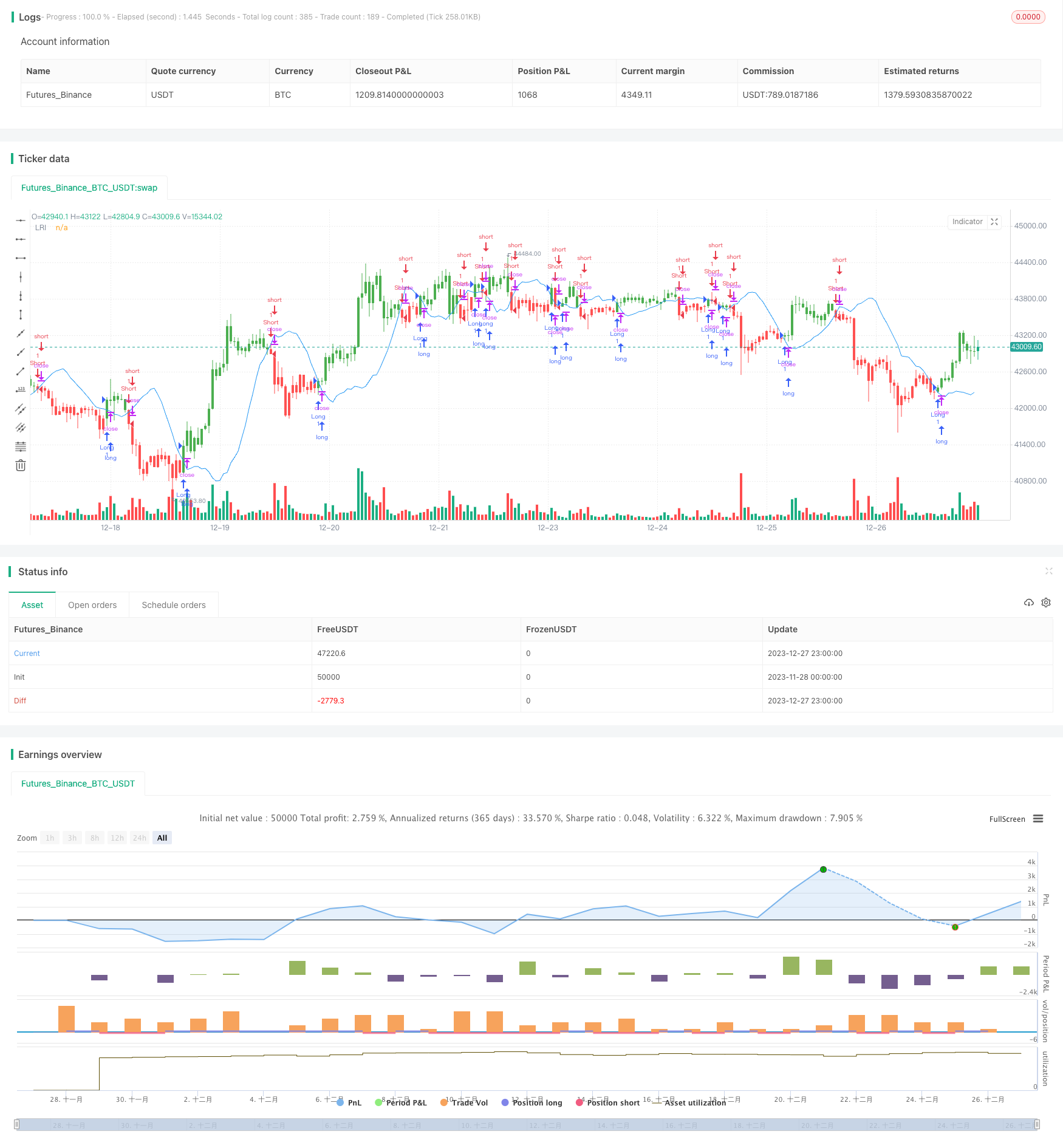
Descripción general

Esta estrategia utiliza la técnica de regresión lineal para calcular los puntos de intersección de regresión lineal y construir una estrategia de negociación cuantitativa con ellos como una señal de compra y venta. La estrategia analiza la secuencia temporal de los precios de las acciones, forma una línea de tendencia de regresión lineal y utiliza los puntos de intersección de regresión lineal para determinar si el precio está sobrevalorado o infravalorado y, por lo tanto, genera una operación de señal.

Principio de estrategia

El punto de intersección de regresión lineal representa el valor de predicción de la serie de tiempo X cuando el valor de Y es 0 (normalmente el precio). La estrategia pre-configura el parámetro Length, con el precio de cierre como la secuencia de origen, para calcular el punto de intersección de regresión lineal de los días más recientes de Length (xLRI). Cuando el precio de cierre es superior al xLRI, se hace más; cuando el precio de cierre es inferior al xLRI, se hace vacío.

La fórmula de cálculo es la siguiente:

xX = Length *(Length - 1)* 0.5  
xDivisor = xX *xX - Length* Length *(Length - 1) *(2 * Length - 1) / 6
xXY = Σ(i *收盘价[i]),i从0到Length-1  
xSlope = (Length *xXY - xX* Σ(收盘价, Length))/ xDivisor
xLRI = (Σ(收盘价, Length) - xSlope * xX) / Length

A través de este cálculo se obtiene el punto de interceptación de regreso lineal xLRI de los días de longitud más recientes. La estrategia determina el alza y bajada de los precios y genera una señal de negociación.

Ventajas estratégicas

La estrategia tiene las siguientes ventajas:

1. Utilizando la técnica de regresión lineal, tiene cierta capacidad de predicción de precios y capacidad de discernimiento de tendencias.
2. Con menos parámetros, el modelo es simple, fácil de entender y de implementar.
3. Se puede personalizar el parámetro Length adaptive para ajustar la flexibilidad de la política.

Riesgos y soluciones

La estrategia también tiene sus riesgos:

1. La simulación de regresión lineal es una simulación estadística basada únicamente en datos históricos y tiene una capacidad limitada para hacer predicciones de movimientos futuros.
2. Los resultados de la regresión lineal pueden no ser válidos si la estructura de la empresa cambia mucho.
3. La configuración incorrecta del parámetro Length puede causar una sobreajuste.

Respuesta:

1. El parámetro Length se abreviará adecuadamente para evitar una sobreadaptación.
2. En la actualidad, la compañía está en proceso de reorganización, pero aún no se ha concretado el plan de reorganización.
3. Utiliza el parámetro de adaptación Length, que se ajusta dinámicamente a las condiciones del mercado.

Dirección de optimización de la estrategia

Esta estrategia también puede ser optimizada en los siguientes aspectos:

1. Aumentar el mecanismo de suspensión de pérdidas para controlar las pérdidas individuales.
2. Combinado con otros indicadores, forma una estrategia combinada para mejorar la estabilidad.
3. Aumentar los parámetros para adaptarse al módulo de optimización y permitir que los parámetros de longitud cambien de forma dinámica.
4. Se ha añadido un módulo de control de posiciones para evitar el exceso de operaciones.

Resumir

Esta estrategia construye una estrategia de comercio cuantitativa simple basada en puntos de detención de regresión lineal. En general, la estrategia tiene cierto valor económico, pero también hay algunos riesgos a tener en cuenta. Se espera que la estabilidad y rentabilidad de la estrategia se mejoren aún más a través de la optimización continua.